Погрешности линейной аппроксимации в прямой ионометрии

Известно [1], что потенциалы мембранных ионоселективных электродов достаточно строго описываются расширенным уравнением Никольского:

E = E ‘± 2,3RT ^zi^F

( lg a+LKa'

I j            7

,

которое учитывает зависимость потенциала не только от активности (концентрации) целевого иона, но также от активности посторонних j -х ионов. Относительную чувствительность электрода к этим ионам характеризуют соответствующие коэффициенты потенциометрической селективности.

В присутствии буфера для регулирования общей ионной силы (БРОИС), уравнение (1) запишем в виде:

E = E '± S lg (ca + а),

где, по предложению [2], а имеет смысл параметра вымывания потенциалопределяющего иона из мембраны. Называют две причины вымывания [2]: растворение ионофора в воде и ионооб- менное вытеснение определяемого иона примесями.

В ионометрических методиках [1, 3–5] в качестве измерительной функции (электродной функции, градуировочной характеристики) чаще используют линейное приближение уравнения (2), то есть вымыванием а пренебрегают. Аппроксимация нелинейной по параметрам функции (2) ее линейной МНК¹-оценкой:

E = E '± S lg c a,                                                                             (3)

должно приводить к систематическим погрешностям метода.

Целью данной работы является исследование систематических погрешностей линейной ап-проксимации2 с использованием математического моделирования сценариев ряда измерительных задач. В качестве прототипов сценариев будем рассматривать аттестованные в разное время методики определения фторида в водах [3–5].

Экспериментальная часть

Методики ионометрического анализа [3–5] включает следующие стадии:

• 1)    подготовку к выполнению измерений, которая включает приготовлении стандартных растворов аналита, а также приготовлении цитратно - ацетатного БРОИС, предназначенного для разбавления стандартных растворов и проб;

• 2)    измерение потенциалов градуировочных растворов и получение градуировочной характеристики (3);

• 3)    выполнение измерения потенциалов проб и отыскание содержания аналита в пробах с использованием функции анализа:

c_A = ant lg

Г E - E')

S

7

Методики ионометрического анализа [3–5] различаются тем, что в методике [3] используют 4 стандартных раствора 1 • 10 ^{- 2}, 1 • 10 ^{- 3}, 1 • 10 ^{- 4}, 1 • 10 ^{- 5} М фторида, которые разбавляют БРОИС в отношении 1 : 2 (методика ГОСТ). Существенно, что концентрация цитрата в анализируемом растворе по методике ГОСТ составляет 5,6 • 10 ^{- 3} М, а концентрация Na₂ЭДТА равна 5,3 • 10 ^{- 4} М.

В методике [4] используют 5 стандартных растворов 1 • 10 ^{- 3}, 1 • 10 ^{- 4}, 6 • 10 ^{- 5}, 2 • 10 ^{- 5} и 1 • 10 ^{- 5} М, которые разбавляют БРОИС в отношении 1 : 1 (методика РД). По методике РД концентрация цитрата в анализируемом растворе составляет 5,0 • 10 ^{- 4} М; БРОИС не содержит Комплексон III.

Методика [5] отличается от методики РД только интервалами определяемых содержаний: от 1 • 10 ^{- 1} до 1 • 10 ^{- 5} при больших и от 1 • 10 ^{- 2} до 1 • 10 ^{- 6} при небольших содержаниях фторида (методика ЭКЭ). За результат анализа в методиках [3–5] принимают среднее двух параллельных определений.

Задача вычислительного эксперимента состоит в математическом описании погрешности определения концентрации аналита вдоль нернстовской градуировочной зависимости (3), тогда как в действительности измеренные потенциалы подчиняются уравнению Никольского. Для определенности решения необходимо задать матрицу плана градуировки, то есть список концентраций в интервале определяемых содержаний, а также число градуировочных растворов. (Мы будем испытывать планы градуировок, описанные в [3–5]). Необходимо также задать параметры уравнения (2).

Коэффициент крутизны S зададим равным коэффициенту Нернста S = 2,3RT / zF. Для простоты примем стандартный потенциал E' = 03. Для задания параметра вымывания воспользуемся результатами работы [6] по влиянию концентрата Na3Cit (в составе БРОИС) на вымывание фторида из LaF3 – мембраны. Установлено, что экспериментальные данные Росса удовлетворительно под- чиняются уравнению:

а = K п - Cit ( с Cit ) ^1/3 + а , = 2 • 10 ^{- 5} ( с Cit ) ^1/3 + 1 • 10 ^{- 7},

где а _s - растворимость LaF₃. Тогда, зная концентрацию цитрата из прописей [3-5], по уравнению (5) легко получить оценки параметров вымывания.

Возможны два варианта решения поставленной задачи: аналитическое решение и алгоритмическое решение. Каждый из вариантов имеет свои достоинства и недостатки. Алгоритмическое решение проще в вычислительном отношении, но имеет численный характер. Аналитическое решение приводит к громоздким уравнениям, вместе с тем анализ этих уравнений позволяет глубже понять свойства результата.

При выводе аналитического решения исходим из того, что равенство правых частей уравнения (2) и уравнения (3) возможно, только если в уравнении (3) присвоить c A =: c A + A c _A, где A c A имеет смысл погрешности вычисленного по уравнению (4) результата определения. Тогда можно записать выражение, связывающее погрешность линейной аппроксимации с концентрацией аналита и параметрами, характеризующими условия анализа:

Д    2,3 ( Е•-^E ■ ) 2,3 ( 5 - ^S )       _$

--~ -----х---х----PF +—— 10^к cS   S   S

Это уравнение является приближенным выражением действительной функции погрешности аппроксимации поскольку при его записи использовали разложение ln(1 + x ) ~ x при x = a /c << 1.

Алгоритмическое решение включает следующие выкладки:

• 1.    В узловых точках градуровки вычисляют потенциалы по уравнению (2). Эта процедура

• 2.    Полученную табличную функцию аппроксимируют по принципу ЛМНК. Находят параметры Ei' и S уравнения (3). Эта процедура подобна восстановлению измерительной функции

• 3.    В заданном интервале определяемых содержаний по уравнению (2) рассчитывают потенциалы для 20 - 30 точек. Эта процедура равнозначны выполнению эксперимента для отыскания приписанных метрологических показателей методики анализа [7].

• 4.    Полученные по п. 3 данные обрабатывают по уравнению (4).

• 5.    Вычисляют относительную погрешность линейной аппроксимации по принципу «задано - найдено». Эта процедура подобна отысканию функции правильности в координатах pF - 8 .

имитирует измерение потенциалов при градуировании.

при градуировке.

Вычисления удобно выполнять в электронных таблицах.

Результаты и их обсуждение

На рис. 1 приведены результаты моделирования кривых правильности для условий анализа, описанных в [3]. Кривые построены в шкале содержаний фторида в его стандартных растворах и пробах. Она отличается от шкалы концентраций измеряемых растворов на коэффициент разведения стандартного раствора раствором БРОИС ( r ). Для перехода к шкале реальных содержаний фторида нужно из номинальных значений абсциссы pF вычесть lg r . В нашем примере lg r = lg(20 / 30) = –0,176 Моделирование осуществляют алгоритмическим способом. Расчеты выполнены для диапазона вероятных значений параметра вымывания. Если исходить из формулы (5) при c _Cit = 5,6 • 10 ^{- 3} М, то a = 3,5 мкМ. Однако эта оценка коэффициента вымывания может быть заниженной, поскольку не учитывает вклады в эффект вымывания других компонентов БРОИС, а также возможные загрязнения фторидом реактивов в составе буферного раствора.

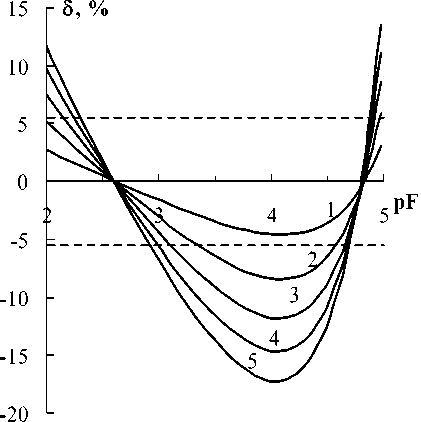
Рис. 1. Функции правильности при моделировании методики ГОСТ с α = 1 (1), 2 (2), 3 (3), 4 (4) и 5 (5) мкМ;

S = 59 мВ, Е ′ = 0 мВ

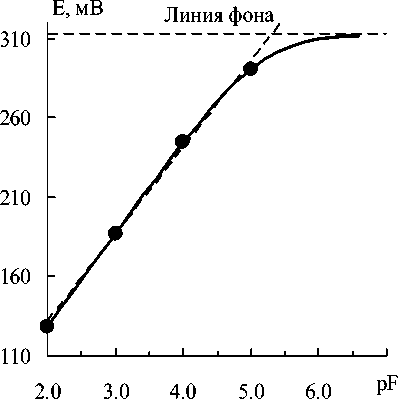
Рис. 2. Электродная функция с параметрами α =5 мкМ, S = 59 мВ, Е ′ = 0 мВ и восстановленное по 4 точкам ее линейное приближение (наклонный пунктир)

Форма функции правильности обусловлена тем, что ЛМНК-приближение является секущей истинной электродной функции (рис. 2). Однако на графике это заметить достаточно трудно даже при значительном вымывании. Вместе с тем, как видим на рис. 1, расхождения между линей- ным приближением и истинной электродной функцией могут в концентрационной шкале достигать 17 % , как при pF4. Линия фона на рис. 2 соответствует потенциалу, обусловленному исклю- чительно вымыванием.

Свойства функции правильности можно проанализировать с использованием уравнения (5).

При больших содержаниях фторида следует ожидать убывающую линейную зависимость 8 от pF. В области малых содержаний, наоборот, функция имеет экспоненциально взрастающий характер.

Точка экстремума кривой погрешности отвечает уравнению:

pF* = - lg а + lg

/ „  2 Л

5 - 5 |

к 5 7

— lg r ,

где pF* - pF минимума. Так для кривой 1 на рис. 1, где ( 5 - 5 ) = 1,1 мВ, pF* = 4,1.

Следует заметить, что формально уравнение кривой ошибок можно попытаться получить из закона переноса погрешностей, применяя его к уравнению (4). Однако закон переноса, при выводе которого используют разложение функции в ряд Тейлора и ограничиваются первыми производными, может объяснить только линейные участки кривых на рис. 1. Для достаточно полного полиномиального описания этих кривых требуется полином четвертого порядка.

Правильность количественного анализа устанавливают, проверяя гипотезу о незначимости систематической погрешности на фоне случайной при выбранной доверительной вероятности Р = 95 % и заданном числе параллельных определений n . Для одновалентных ионов случайную составляющую метода градуировочного графика принято оценивать уравнением для относительного стандартного отклонения единичного определения в генеральной совокупности [7]:

^о r , c

2,3 о E

S

где о E - стандартное отклонение измерения потенциала, которое обычно принимают равным 1 мВ и считают независящим от значения потенциала. Уравнение (7) получают, применяя закон переноса случайных погрешностей к функции анализа типа (3)⁴. При двухсторонней проверке будем использовать пределы:

A r , c = ± z 0,975 5 ^E , ⁽⁹⁾ где квантиль стандартного нормального распределения z 0,975 = 1,96.

Заметим, что недавно [8] предпринята попытка «уточнения» уравнения (7). Однако при выводе своего уравнения автор фактически рассматривает принципиально другой метод анализа, который называют методом сравнения (или методом внешнего стандарта). Уравнение погрешности метода одноточечной градуировки хорошо известно [9, с. 67]. Кроме того, автор [8] не заметил различий между выборкой и генеральной совокупностью. В генеральной совокупности коэффициенты электродной функции – это детерминированные величины, в отличие от их МНК-оценок. При использовании закона переноса погрешностей с коэффициентов выборочной измерительной функции (3) на аналитическую функцию (4) получают другое известное уравнение, см. [9, с. 172], которое мог бы получить автор [8] при последовательном подходе.

Вычисленные по уравнению (9) верхняя и нижняя границы вероятных случайных составляющих погрешности изображены на рис. 1 пунктирными линиями. Видим, что только в случае с а = 1 мкМ систематическая погрешность полностью вписывается в доверительную область. Гипотеза об отсутствии систематической погрешности результатов анализа не отвергается во всем интервале измеряемых содержаний. В остальных случаях результаты статистических испытаний сложным образом зависят от концентрации фторида в испытуемых образцах. А это, в свою очередь должно порождать трудности отыскания приписанных характеристик правильности и точности методики анализа.

Функция правильности зависит не только от концентрации потенциалопределяющих ионов, но также от плана построения градуировки, то есть от выбора рабочего интервала концентраций, способа его разбиения на поддиапазоны, а также числа реперных точек. Следуя нашей методике можно, получать планы, минимизирующие погрешности линейной аппроксимации.

На рис. 3 сравниваются результаты моделирования функций правильности для методики РД (А) и для методики ЭКЭ (Б). Состав БРОИС в том и другом случаях одинаков. Одинаков также вычисленный по уравнению (5) параметр вымывания а = 1,6 мкМ. Градуирование в обоих случаях проводят по 5 образцам сравнения. Но существенно различаются рабочие интервалы градуировок и расположение реперных точек в этих интервалах: 1 • 10 - 3 , 1 • 10 - 4 , 6 • 10 ^{- 5}, 2 • 10 ^{- 5}, 1 • 10 ^{- 5} М (РД) и 1 • 10 ^{- 1}, 1 • 10 ^{- 2}, 1 • 10 - 3 , 1 • 10 - 4 , 1 • 10 ^{- 5} М (ЭКЭ).

Даже при поверхностном сравнении данных на рис. 3, можно сделать вывод о большей эффективности плана градуировки по методике РД. Систематические погрешности аппроксимации меньше по абсолютной величине и они равномернее распределены в центральной части кривой. Поэтому введение поправок в результаты анализа здесь упрощается.

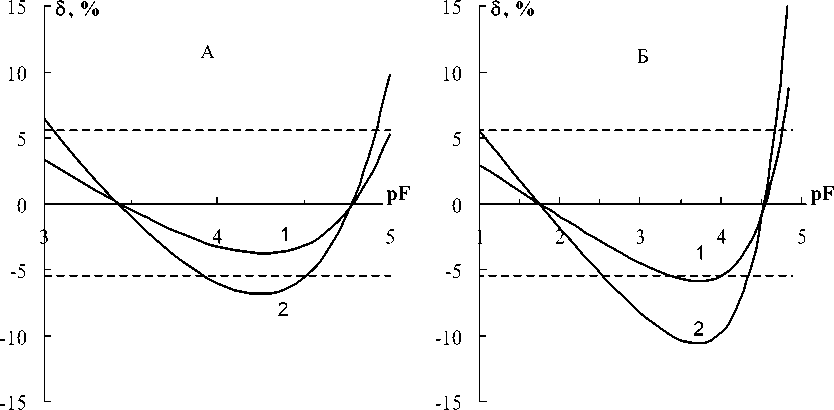
Рис. 3. Функции правильности при определении фторида по методике РД (А) и по методике ЭКЭ (Б) при α = 1 (1) и 2 мкМ (2) (Области случайных погрешностей выделены пунктиром)

Значения 8 , которые находятся снаружи доверительных границ (см. рис. 1 и рис. 3), взятые с обратным знаком, называют поправками. Здесь введение поправок на влияние систематических погрешностей возможно. Значения 8 , которые накрывает доверительная область, рассматривают как неисключенные остатки систематических погрешностей. Погрешность результата косвенного измерения оценивают на основе композиции распределений случайных и неисключенных систематических погрешностей.

Согласно нормативным документам предпочтительны методики без поправок. В рамках линейной модели проблему поправок можно решить изменением положения нижней границы интервала определяемых содержаний с н . Для этого перепишем уравнение (2):

а

Е = Е ‘± 5 lg c a ± 5 1g 1 + —| = En ± 5 1g 1 + —I ,

v    c A

v    c A

где E_N – это нернстовская линейная по параметрам часть потенциала. Нелинейную по параметру а часть электродной функции можно линеаризовать:

(

Е - En =± 5 lg 1 + — V    c A

± 5 а

2,3 c A

.

Потребуем, чтобы c A = c н , когда выполняется условие:

|Е - En\ < z "

.

n

Объединив (12) и (11), получаем выражение для оценки концентрации аналита в градуировочном растворе на нижней границе определяемых содержаний:

c н >-----------а.

²,³ z 0,95 ° Е

Вычисленные по уравнению (13) значения нижних границ определяемых содержаний в зависимости от величины параметра вымывания и условий оценки приведены в таблице. Эти границы соответствуют концентрациям стандартных растворов до их разведения БРОИС в отношении 1 : 1. Из этих данных следует, что тест на соответствие потенциала нижней границы определяемы содержаний нернстовскому участку электродной функции будет положительным, если предельная концентрация в 20–40 раз превышает вымывание. Конечно, столь существенное сокращение интервала определяемых содержаний нельзя считать приемлемым для большинства аналитических задач ионометрии. Что касается контроля содержания фторида на уровне ПДК 1,7 мг/л (pF = 4,38) [10], то, с некоторыми оговорками, это значение вписывается на рис. 3 в наши оценки нернстовского участка электродной функции. Если, крое этого, учесть норматив точности [10] определения фторида, который установлен на уровне ±15 %, то нижнюю границу можно сдвинуть до pF = 5, как это, по-видимому, сделано в методиках [3–5]. Это предположение подкрепляется данными на рис. 1 и 3.

Показатели концентраций аналита на нижних границах определяемых содержаний

Условия оценки	Параметры вымывания, мкМ
	0,5	1	2	3	4	5
n = 2; P = 0,95	4,73	4,43	4,13	3,95	3,83	3,73
n = 2; P = 0,99	4,85	4,55	4,25	4,07	3,95	3,85
n = 1; P = 0,95	4,81	4,51	4,20	4,03	3,90	3,81
n = 1; P = 0,99	5,00	4,70	4,40	4,22	4,10	4,00

Статистический анализ функций правильности на рис. 1 и 3 будет неполным без исследования мощности тестов [11]. Мощность теста (мощность критерия) характеризует надежность статистического вывода вероятностью непринятия нуль-гипотезы Н⁰, когда верна альтернатива Н а . Формула для мощности теста при двухсторонней проверке Н 0 : | А r,c | < |8| имеет вид [12]:

1 -р = 1 -ф ( _{Z 1} -_a/ 2 + х ) + ф ( z _а/ 2 +х ) , (14)

где параметр сдвига X - это

Х = —.                                                          (15)

^ r , c

Значения функций распределения Лапласа - Гаусса и их квантилей берут из статистических таблиц или вычисляют в электронных таблицах с использованием встроенной библиотеки статистических функций. Так в нотации Excel уравнение (13) имеет вид:

=1-НОРМСТРАСП(НОРМСТОБР(0.975)+ Х )+НОРМСТРАСП(НОРМСТОБР(0,025)+ Х ).

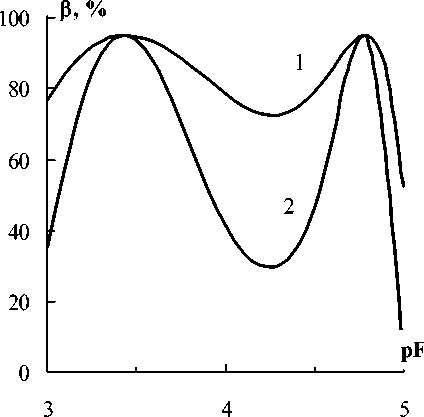
Рис. 4. Вероятности необнаружения систематических погрешностей вдоль функций правильности на рис. 3А: 1 - при α = 1 мкМ; 2 - при α = 2 мкМ

В нашем тесте интерес представляет частота событий когда отвергается Н а , хотя она и верна. Вероятности таких событий ( р ) называют вероятностью ошибки II рода. Она дополняет по вероятности мощность теста. Значения р для примера на рис. 3А приведены на рис. 4.

Видим, что существует значительная вероятность принятия решения о введении поправок, даже если систематические погрешности не выходят из доверительных границ.

Из исследования результатов моделирования функций правильности можно сделать вывод о том, отыскание и введение поправок в результаты анализа при линейной аппроксимации электродной функции сопряжено со значительными трудностями. Очевидно, что затруднений можно избежать, если в качестве измерительной функции использовать расширенное уравнение Никольского (2). Аппроксимация данных ионометрии уравнением Нернста, которую широко используют в современ- ных иономерах, сегодня вряд ли оправдана. (Если иметь в виду широкую доступность математических пакетов для ПЭВМ и повсеместную компьютеризацию аналитических приборов.)

В качестве примера рассмотрим использование утилиты Excel «Поиск решения» (Solver) для восстановлени нелинейной по параметрам градуировочной функции типа Никольского.

Эффективность Solver исследовали на ряде тестирующих примеров. Один из наиболее значимых примеров содержал вычисленные по уравнению (2) данные о градуировке по четырем точкам. Концентрация аналита в стандартных растворах: 1 • 10 - 5 , 1 • 10 - 4 , 1 • 10 - 3 , 1 • 10 - 2 М. Параметры уравнения (2): E' = 0 мВ; S = 58,20 мВ⁵; а = 1 • 10 - 6 М. Эти параметры характеризуют достаточно сложную ситуацию для структурной и параметрической идентификации измерительной функции Никольского.

Параметры восстанавливали безусловным оптимизационным методом Ньютона6 при минимизации суммы квадратов невязок (SS) между заданными и найденными значениями потенциа- лов. Наилучшую сходимость итерационного процесса удается получить для SS = SS(E', S, lgа). При этом в качестве стартовых параметров можно задавать E' = ±59 мВ; S = 59 мВ; а = 1 • 10-7 М.

С этими начальными приближениями параметров найдено: E‘ = 0,00024 мВ; S = 58,200 мВ; а = 1,000^10-6 М с остаточной дисперсией SS = 1,2 • 10-7. Видим, что восстановленная функция практически не отличается от заданной и решение является устойчивым.

Для обработки результатов анализа с нелинейной градуировкой достаточно подставить измеренное значение потенциала пробы в уравнение:

. L E - E')

-a = ant lg l± —s— I - а, которое не требует численного решения. Для тестирующего примера при заданном содержании аналита 1,00000 • 10-5 М по уравнению (16) найдено 1,00001 •Ю-5 М. То есть погрешность определения составляет тысячную процента, что можно объяснить погрешностями округления.

Задачу восстановления нелинейной градуировки типа Никольского можно упростить, если к измерениям потенциалов образцов сравнения добавить измерение потенциала фона, см. рис. 2. Измерительная функция, с поправкой на фон, имеет вид:

E - E _ф0 н = ± S lg 1 1 + - A I . (17)

V а J

В этом уравнении только два подгоняемых параметра. Это обстоятельство существенно уп- рощает выбор начальных приближений S и а, а также их уточнение методом Ньютона. При тестировании нашли S = 58,200 мВ; а = 1,00000 • 10-6 М с остаточной дисперсией 1 • 10-6. Для обра-

ботки результатов используют уравнение:

c _A

(

= а ant lg ±

V V

E - E фон ^

S J

^- 1,

В заключении отметим, что проблема погрешностей линейной аппроксимации в ионометрии существует и может быть разрешена с использованием предлагаемого подхода. Описанные в работе варианты получения нелинейной градуировочной характеристики и обработки результатов анализа можно рекомендовать для использования при разработке и оптимизации ионометриче- ских методик.

Выводы

• 1.    Предложен алгоритмический метод исследования систематических погрешностей аппроксимации нелинейной электродной функции уравнением линейной регрессии при ионометрическом анализе.

• 2.    Выведено уравнение функции правильности. Приведены примеры его использования для прогнозирования свойств погрешностей линейной аппроксимации.

• 3.    Предложено уравнение для оценки нижней границы определяемых содержаний, являющейся началом «нернстовского участка» электродной функции.

• 4.    Предложена методика исследования статистической значимости систематических погрешностей аппроксимации, включающая вычисления мощности теста.

• 5.    Показано, что наиболее эффективным способом избежать введения поправок в результаты ионометрии является использование в качестве измерительной функции обобщенного уравнения Никольского.

• 6.    Приведены примеры решений уравнения Никольского относительно его параметров с использованием встроенного в электронные таблицы метода Ньютона.