Поиск неподвижной точки монотонного отображения полуупорядоченного топологического пространства

Существует большое число работ, посвященных приближению неподвижных точек отображений. Широко известен метод последовательных приближений (метод Пикара -Банаха. [1], а. также его варианты [2-4]. Различают два. подхода, к его обоснованию. В первом подходе [1-4] сходимость метода, основана, на. сжимаемости отображений на. всей области определения. Для случая многозначных отображений используется обобщенный принцип сжимаемости [5]. В работах [6-10] сходимость метода доказывается для отображений со специальными метрическими свойствами.

Во втором подходе требуется монотонность отображения. Классическим результатом в теории неподвижных точек монотонных отображений частично упорядоченных множеств является теорема. Тарского [11] и ее развитие в виде теоремы Кнастера. - Тарского [12], © Рябиков А. И., 2023

«Московский физико-технический институт (национальный исследовательский университет)», 2023

в которой для существования неподвижной точки требуется существование точной верхней грани для любого линейно-упорядоченного подмножества отображаемого множества. Для непрерывных функций можно потребовать существование точной верхней грани лишь для любого счетного линейно-упорядоченного подмножества. Для таких функций верна теорема Тарского - Канторовича [13], на основе которой можно получить итерационный алгоритм поиска неподвижной точки. Обобщения результатов Тарского - Канторовича на случай поиска точек совпадений однозначных и многозначных отображений даны в работах [14] и [15]. Альтернативная совокупность требований для сходимости итерационного метода сформулирована Клини [16].

В данной работе рассматривается метод последовательных приближений в том случае, когда непрерывное и монотонное отображение задано на полуупорядоченном топологическом пространстве, причем существование точной верхней грани у любого частично упорядоченного подмножества не требуется. Получены необходимые и достаточные условия сходимости итерационного процесса приближения неподвижной точки отображения для любой начальной точки из некоторого подмножества.

2.    Теорема о сходимости итерационных процессов

Рассмотрим задачу приближения неподвижной точки монотонного и непрерывного отображения f : X ^ X, необязательно удовлетворяющего требованию сжимаемости. Под X будем понимать топологическое пространство, в котором задано отношение частичного порядка. Предполагается, что топологическое пространство обладает некоторыми свойствами, связывающими его систему открытых множеств с отношением строгого порядка, а именно:

• 1)    для любой возрастающей ограниченной последовательности D = {х_п }„2д существует точная верхняя грань, являющаяся точкой прикосновения множества D;

• 2)    для любых х < у интервал (х,у) является непустым связным множеством;

• 3)    для любых х < у найдутся окрестности О_ж и Оу то чек х и у, такие, что каждый элемент О _ж предшествует каждому элементу Оу, т.е. О _ж -< Оу.

Определение 1. Множество назовем ограниченным сверху, если любая возрастающая последовательность элементов этого множества ограничена.

Определение 2. Возрастающую последовательность {х_п}⁺=д назовем сходящейся к точке х*, если последовательность имеет точную верхнюю грань х*.

Отметим, что в случае метрического пространства сходимость возрастающих последовательностей в смысле определения 2 совпадает с обычной сходимостью. Тем не менее в данной работе не предполагается метризуемость топологического пространства X и не требуется сходимость произвольной неупорядоченной последовательности элементов пространства.

Введем обозначение Bf = {х Е X|f(х) > х}. Предположим, что Bf - непустое множество. Рассмотрим итерацию метода последовательных приближений, т.е. изучим семейство последовательностей {хп}+=0, порождаемых хд Е Bf и рассчитываемых согласно формуле х«+1 = f (хп),п = 0,1,....                                   (1)

Сформулируем теорему о сходимости возрастающей последовательности {х_п}+=д, где х_д Е Bf.

Теорема 1. Для того чтобы последовательности {х_п}+=д для любого хд Е Bf сходилась к некоторой (может быть, зависящей от хд) неподвижной точке х* отображения f : X ^ X, необходимо и достаточно, чтобы существовала система попарно непересека-ющихся открытых и ограниченных сверху множеств, покрывающих Bf.

Доказательство. Необходимость. Обозначим через X* множество всех неподвижных точек, к которым сходятся последовательности, порождаемые начальными точками из B f и рассчитываемые согласно формуле (1). Рассмотрим систему попарно непересекающихся множеств иж* = {жд G Bf | впр{/п(жд)} = ж*}, где ж* G X*,                     (2)

покрывающих Bf. Очевидно, что любое множество из (2) является ограниченным сверху. Покажем теперь, что (2) - система открытых множеств.

Возьмем произвольное U_x* и рассмотрим интервал (жд,/(жд)), где жд G U_x*. Для точек жд и /(жд) найдутся окрестности Охд и О/(жд) точек, та кие, что Ожд ^ О/(жд). В силу непрерывности / множество 8жд = /^-1О/(жд) О Ожд является непустой окрестностью жд и при этом 8жд ^ /(8жд). В частности, будут выполнены неравенства жд ^ /(8жд) и 8жд -< /(жд). С учетом монотонности /, пол учим впр{/^п(8жд)} = ж*, следовательно, окрестность точки жд лежит в U_x*. Необходимость доказана.

Достаточность. Пусть существует система попарно непересекающихся открытых и ограниченных сверху множеств, покрывающих Bf, т.е. Bf С (jUa. Возьмем произвольную а точку жд G Bf. Существование покрытия Bf означает, что найдется ад. что жд G Ua0. Покажем, что все элементы последовательности {жп}+Дд лежат в множестве Ua0.

Из монотонности / следует, что все точки ж_п и интервалы (ж_п,/ (ж_п) , п = 0,1,..., лежат в Bf. Предположим, что пайдется пд. что точки ж_п0 и /(ж_п0) лежат в различных непересекающихся открытых множествах U_a0 и |J U_a из покрытия Bf. Интервал а=ао

(жп0, /(жп0)) является непустым связным множеством, а значит, найдется точка из этого интервала, не принадлежащая ни Ua0, ни |J Ua. Это противоречит тому, что интер-а=ао вал (жп0, /(жп0)) С Bf. Таким образом, все элементы возрастающей последовательности {жп}+Дд лежат в Uao. Из ограниченности сверху множества Ua0 следует существование ж* = впр{жп}. Покажем теперь, что /(ж*) = ж*.

Действительно, ж_п < ж*, п = 0,1,..., следовательно, /(ж*) является верхней гранью последовательности {ж_п}+Дд.

Пусть ж* < /(ж*). Как показано ранее, найдется окрестность 8ж* тонки ж*, что ж* -< /(8ж*). Тонка ж* является тонкой прикосіювешія множества {ж_п}+=д. а. 'значит, найдется ж_п0 G 8ж*. Но это означает, что ж* < /(ж_п0). Получили противоречие с ж_п0₊₁< ж*. Таким образом, /(ж*) = ж*. Теорема полностью доказана.                             □

Замечание. Отметим, что множество U [жп, /(жп)] является подмножеством Bf. Таким п образом, отрезками [жп, /(жп)] можно строить внутреннюю аппроксимацию множества Bf.

Пример. Рассмотрим пример топологического полуупорядоченного пространства, не являющегося решеткой. Возьмем в качестве X круг с единичным радиусом на плоскости Д2, в котором задано отношение строгого порядка по Слейтеру, т.е. ж < у, если ж^ < у^ для всех г = 1, 2. Очевидно, что все три свойства топологического пространства выполняются. Рассмотрим монотонное и непрерывное отображение / : X ^ X жі - 1 8Іл(^жі)

/ (жі, ж2) = а         V             ,                                   о v         ж2 + V ВШ^)

где fc = 6л, а = 0.9. На рис. 1 пунктирной линией показана Гранина множества X. Серым цветом выделены попарно непересекающиеся открытые и ограниченные сверху множества, покрывающие Bf. В углах множеств отмечены неподвижные точки отображения (3).

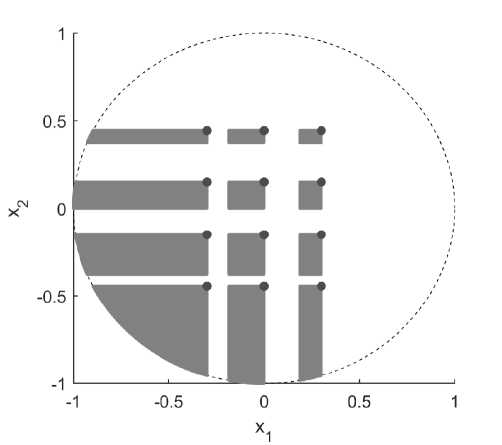
Рис. 1. Множество Bf и неподвижные точки отображения (3)

Следствие 1. Пусть f : R₊ ^ R+ - непрерывная функция, не убывающая по своему аргументу. Для того чтобы последовательность {ж_п}+= для любого жд Е R+ сходилась к некоторой (может быть, зависящей от жд) неподвижной точке ж* отображения f, необходимо и достаточно, чтобы для любого у > 0 бесконечньш отрезок [у, +то) не принадлежал Bj.

Доказательство. Необходимость. По теореме 1 существует система попарно непере-секающихся открытых и ограниченных сверху множеств, покрывающих Bj. Это означает, что для любого у > 0 бескопечпьш отрезок [у, +то) нс принадлежит Bj. Необходимость доказана.

Достаточность. Итак, пусть для любого у > 0 бесконечньш отрезок [у, +то) не принадлежит Bj. Тогда найдется неограниченная возрастающая последовательность точек {у_п}+=д, ^не принадлежащих Bj. Значит, существует система попарно непересекающихся ограниченных интервалов (у_п,у_п+1), г де п = 0,1,..., покрывающих Bj. В случае 1, когда жд Е Bj, следствие 1 доказан о. В случае 2, когда f (жд) < жд, рассмотрим неубывающую функцию <р(ж) = —f (-ж) при ж < 0. Множество B_v ограничено сверху, и по теореме 1 последовательность {ж_п}+=д сходится к неподвижной точке функции f. Следствие 1 полностью доказано. □

3.    Применение следствия теоремы 1 к прикладной задаче

В [17] рассматривается задача выбора правил управления каскадом водохранилищ. Выбор правил управления каскадом водохранилищ основан на вариантных расчетах, в рамках которых используется многошаговая динамическая модель каскада. Для проведения вариантного расчета требуется задать начальные значения объемов воды в водохранилищах. Тогда, используя балансовое уравнение и изучаемое правило управления, можно последовательно, начиная с самого верхнего водохранилища каскада, рассчитать величины попусков через плотины и объемы воды во всех водохранилищах на шаг вперед. Проблема состоит в том, что различие начальных и конечных объемов воды на траектории, построенной для заданных параметров правил управления, означает использование дополнительного водного ресурса (или его экономию) и делает различные варианты параметров несравнимыми. В работе [18] сформулирована зависимость конечного объема воды от начального в виде непрерывной и монотонной функции f неотрицательного аргумента и предложен алгоритм нахождения подходящих значений начальных объемов воды в водохранилищах на основе метода последовательных приближений. Следствие 1 позволило получить важные результаты при решении задачи выбора правил управления каскадом водохранилищ:

обосновать алгоритм поиска подходящих значений начальных объемов водохранилищ и сформулировать условие безопасности правил попуска.

4.    Заключение

Доказанная теорема 1 обосновывает существование неподвижной точки отображения f. Отметим, что неподвижная точка в общем случае может быть не единственной и зависеть от выбора начальной точки итерационного процесса.

Автор благодарит Кукушкина Николая Серафимовича за помощь в подготовке статьи.