Поиск всех решений задачи динамического программирования в случае совпадения их многокритериальных оценок

Высокая эффективность математических методов в естественных, технических и экономических науках постоянно получает практические подтверждения [1–10]. В частности, в экономической отрасли хорошо зарекомендовал себя метод динамического программирования (ДП) [1–3, 5–7]. С помощью этого метода удается организовать эффективное управление многошаговыми процессами в сферах распределения инвестиций, управления ресурсами, сетевого планирования и др.

Широкое распространение схемы ДП определяет актуальность задач ее совершенствования. Одним из недостатков этой схемы является невозможность вычисления всех решений задачи при совпадении их критериальных оценок.

Поясним сказанное на примере. При рассмотрении экономических задач на практике довольно часто используется алгоритм классической задачи о рюкзаке. Причем используется задача именно о так называемом «целочисленном рюкзаке».

Пример 1. Заданы n вещей, их размеры wi, стоимости si, и некоторое число H – вместимость рюкзака (все числа – натуральные). Требуется найти количество штук zi каждой вещи, чтобы выполнялось n условие ∑ z w ≤ H и при этом суммарная ценность i=1

n вещей f = ∑ z s была максимальной. i=1

Применим для решения представленной выше задачи метод ДП. Найдем решения при следующих данных: количество вещей n = 4;

габариты (или размеры) w = (2; 3; 5; 7); стоимость каждой вещи s = (3; 5; 8; 11) и вместимость рюкзака H = 10. При таких исходных данных получим ответ: z = (2; 2; 0; 0), fmax = 16.

Однако несложно убедиться, что укладка z = (1; 1; 1; 0) тоже является оптимальным решением. Очевидно, алгоритм ДП выбрал первый вариант из-за того, что при поиске максимального элемента в некотором наборе ответом всегда является первый из одинаковых максимальных элементов.

Согласно классическому определению, точка x* называется точкой максимума функции ϕ(x) на множестве Х, если ϕ(x*) ≥ ϕ(x) для всех x∈Х. Т.е. в определении записано нестрогое неравенство. Отсюда, если Х – конечное множество, на котором целевая функция имеет несколько точек максимума, то из сформулированного определения следует, что при буквальном следовании ему в выбор должны попасть все эти точки. Тогда в примере 1 необходимо предусмотреть следующие ситуации при решении. Если при решении учитывать порядок следования вещей при укладке вещей в рюкзаке, то мы получим 15 вариантов оптимального управления процессом укладки вещей с одинаковым значением целевой функции. Если не определять порядок укладки вещей в рюкзаке – четыре решения (2, 2, 0, 0), (1, 1, 1, 0), (0, 1, 0, 1), (0, 0, 2, 0).

Число подобных дублирующих вариантов в прикладных задачах большой размерности также может быть очень большим, а так как их критериальные оценки одинаковы, то в традиционной схеме ДП не принято тратить вычислительные ресурсы и находить их все – достаточно выбрать какое-то одно решение. Тем не менее, существует немало практически важных задач, решаемых методом ДП, в которых надо найти не просто одно первое попавшееся оптимальное решение, но найти все такие решения. В частности, это касается известной задачи поиска критического пути в сетевом графе при реализации метода PERT управления проектами. В процессе решения этой задачи для вычисления резервов времени выполнения работ, запланированных в проекте, необходимо определить вершины, лежащие на критическом пути. Если же таких путей несколько, то возникает неоднозначность в оценках, особенно в том варианте метода, при котором критический путь может меняться на итерациях решения более общей задачи [10].

В общем случае само существование нескольких оптимальных траекторий многошагового процесса с большой вероятностью может означать, что задача поставлена не вполне корректно, в том смысле, что назначенные критерии не полно характеризуют исследуемую систему. Тогда для выбора оптимального варианта придётся прибегать к каким-нибудь вспомогательным процедурам, возможно, с подключение новых критериев. А раз так, то вполне возможно, что именно среди траекторий, не найденных на первом этапе, и находится оптимальное решение.

Это означает, что необходимо доработать традиционную схему ДП на случай существования нескольких оптимальных траекторий с одинаковым значением критерия. В данной статье предлагается наиболее общий вариант такой доработки, а именно, обобщению подвергается многокритериальная схема ДП.

Методы

Решение дискретной задачи оптимизации многошагового процесса методом ДП удобно описывать в терминах теории графов. В этом случае получаем задачу поиска оптимального пути на ориентированном графе.

Существуют две схемы нахождения оптимальных решений данной задачи. Первая связана с запоминанием условно-оптимальных решений при первом проходе алгоритма. Вторая схема основана на восстановлении траекторий. При первом проходе запоминаются только критериальные оценки условно-оптимальных траекторий. При втором проходе оптимальное решение определяется на основе ключевого равенства, которое в терминах задачи поиска оптимального пути на графе имеет вид:

D ( v ) = D ( u ) + p ( u, v ),           (1)

где v - очередная анализируемая вершина, u - вершина, предшествующая v , p ( u, v ) - длина дуги ( u, v ), D ( x ) - найденная при прямом ходе протяженность (критериальная оценка) оптимального пути из начальной вершины в вершину x . Для текущей вершины v выбирают смежную с ней вершину u , удовлетворяющую равенству (1). Её считают следующей вершиной оптимального пути, полагают v = u и процесс восстановления продолжается до достижения начальной вершины.

Воспользуемся второй схемой для разработки алгоритма восстановления всех оптимальных решений многокритериальной задачи поиска оптимальных путей на графе. Его наиболее подходящий для данного случая прототип опубликован авторами в [11].

Пусть задан граф G , каждая дуга ( u, v ) которого снабжена векторным весом A [ u, v ], вес произвольного пути равен сумме весов составляющих дуг, и на множестве весов дуг и путей задано некоторое бинарное отношение предпочтения R . Требуется определить все пути, веса которых не доминируются в смысле отношения R , в том числе надо найти и пути с совпадающими критериальными оценками. Сокращённо искомые пути назовём R -оптимальными.

Введем следующие обозначения:

• -    V - множество вершин графа;

• -    s, f - начальная и конечная вершины искомых путей;

• -    p ( u, v ) - часть пути p , соединяющая лежащие на нём вершины u и v ;

• -    F(p ) - многокритериальная оценка длины пути p (целевая вектор-функция);

• -    { D [ v ]} - множество оптимальных векторных весов путей из начальной вершины (источника) s в вершину v , полученное в результате работы алгоритма;

• -    ПР [ v ] - список вершин графа, предшествующих вершине v ;

• -    C^R ( X) - множество значений функции выбора на X , определяемой механизмом блокировки по заданному бинарному отношению R ;

• -    a ^ L - операция исключения элемента а из списка L .

Сделаем следующие предположения.

• 1.    В графе G каждая пара вершин может соединяться не более чем одной дугой.

• 2.    Векторный вес любого контура, имеющегося в графе, доминируется в смысле отношения R нулевым вектором.

• 3.    Отношение R транзитивно, асимметрично и инвариантно относительно добавления произвольного элемента. Последнее свойство означает, что для любых трёх элементов x, у, b е E m следующие отношения эквивалентны:

xRy и ( х + b ) R ( y + b ).

Обсуждение

Решение задачи разбивается на три этапа. Опишем их на неформальной версии языка PASCAL.

• 1 этап. Построение оптимальных критериальных оценок для путей из начальной вершины s во все остальные.

Предлагается следующий алгоритм 1, представляющий собой многокритериальный вариант известного метода Форда - Беллмана.

for v е V \ { s } do { D [ v ]}: = { A [ s, v ]};

{ D [ s ]}: = 0 ;

for k: = 1 to n - 2 do for v е V \ {s} do for u е ПР[v] do for q е {D[u]} do

{ D [ v ]}: = C R ({ D [ v ]} U { q + A [ u, v ]});

Корректность данного алгоритма доказывает следующая теорема, являющаяся частным случаем более общей теоремы из [11].

Теорема 1. Если граф G и бинарное отношение R удовлетворяют предположениям 1 - 3, то множество оценок, полученных алгоритмом 1, совпадает с множеством оценок R -оптимальных путей графа.

• 2 этап. Построение графа R -оптимальных путей.

Отбираются дуги, составляющие часть R-оптимальных путей. Из них затем формируется подграф G 1, в котором все пути R-оптимальны. Данный блок алгоритма (алгоритм 2) выглядит так for v е V begin ПР Eq [v]: = ПР[v];

for u е Пр [ v ] do

• begin M: = true ;

for z е {D [v]} do for y е {D[u]} do if z = y + A [u, v] then

• begin M: = false; break; end ;

• if not ( M ) then break ;

• if M then u ^ ПР_Eq [ v] ;

end;

end;

• < Формирование графа по спискам предшествования ПР_Eq [ v] >

В традиционной схеме с восстановлением путей этапы поиска подходящих дуг и построение оптимальных путей совмещены в одном блоке.

Однако при наличии равновеликих путей приходится сохранять варианты в соответствующих структурах данных, (подграф G 1 ) а затем на третьем этапе выявлять все возможные решения. Как видно из описания алгоритма, отбор дуг, составляющих решение задачи, основан на выполнении следующего условия.

• ∃ z ∈ { D [ v ]} ∃ y ∈ { D [ u ]}: z = y + A [ u, v ]. (2)

При его выполнении вершина u остаётся в списке предшествования ПР_Eq [ v] .

Результат работы алгоритма 2 приведён на рисунке 1. Дуги исходного графа снабжены двумя критериями, указанными в скобках. Задача состоит в поиске всех Парето-оптимальных путей из вершины s = 1 в вершину f = 5. Всего из вершины s = 1 в вершину f = 5 ведут три Па-рето-оптимальных пути, два из которых имеют совпадающие критериальные оценки.

Отметим очевидный факт, что алгоритм не создаёт в графе новых вершин и рёбер, а только исключает рёбра, не удовлетворяющие равенству (2). Поэтому, любая вершина, дуга или путь, имеющиеся в графе G 1 , также присутствуют в G . Открытым остаётся лишь вопрос о соответствии произвольных путей в графе G 1 R -оптимальным путям в G . Ответ даёт следующая теорема.

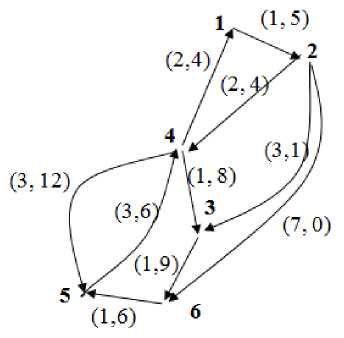
Рисунок 1. Исходный граф

Figure 1. Graph

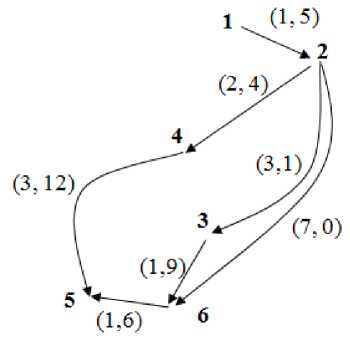
Рисунок 2. Граф со списками предшествования ПР_Eq [ v]

Figure 2. Graph ПР_Eq [ v]

Теорема 2. Пусть подграф G 1 графа G задан списками предшествования ПР_Eq [v], v ∈ V , которые построены по алгоритму 2 (рисунок 2). Тогда множества всех R -оптимальных путей на графе G и путей на подграфе G 1 из начальной вершины s в конечную f совпадают.

В [11] доказана теорема, которая утверждает, что при сформулированных допущениях 1 – 3 каждая часть R -оптимального пути графа также R -оптимальна. Обозначим это свойство сокращённо «свойство [11]». Им мы воспользуемся при доказательстве теоремы 2.

Доказательство. Пусть p ∈ G – произвольный R -оптимальный путь из s в f . Покажем, что p ∈ G 1 . Рассмотрим вторую от начала пути p вершину v . Для нее справедливо равенство (2) при u = s , поскольку D [ s ] = 0, и вершины s и v соединяет единственная дуга. Следовательно, s ∈ ПР_Eq [ v ], а значит, ( s, v ) ∈ G 1 .

Далее, по предположению индукции, допустим, что для произвольной вершины u ∈ G вся часть p (s, u) пути p от s до u принадлежит G 1 , и пусть v – следующая вершина пути p . Покажем, что ( u, v ) ∈ G 1 .

Очевидно, F ( p (s, u) ) + A [ u, v ] = F ( p (s, v) ).

Но согласно свойству [11], части p (s, u) и p (s, v) пути p R -оптимальны, и, следовательно, F ( p (s, u) ) ∈ { D [ u ]} и F ( p (s, v) ) ∈ { D [ v ]}. Значит, при y = F ( p (s, u) ) и z = F ( p (s, v) ) выполняется равенство (2) и при работе алгоритма 2, дуга ( u, v ) не будет исключена и ( u, v ) ∈ G 1 .

Отсюда, по индукции следует, что весь путь p принадлежит G 1 .

Обратно. Пусть на подграфе G 1 q – произвольный путь из s в f . Покажем, что на графе G он является R -оптимальным.

Рассмотрим его первое ребро ( s, t ). Т.к. по условию это единственное ребро, соединяющее s и t , то оно является R -оптимальным путём из s в t на графе G . Иными словами, для первого ребра пути q требуемое утверждение верно.

Предположим, что для произвольной вершины u ∈ q вся часть q (s, u) пути q от s до u является R -оптимальным путем из s в u на графе G , и пусть v – следующая вершина пути q . Покажем, что составной путь q ( 5 , и )&( u , v ) е q является R -оптимальным на G .

Согласно алгоритму 2, дуга ( u, v ) остаётся в графе G 1 в том, и только в том случае, если одновременно выполнены три условия:

F(q (s, u)) ∈{D[u]}, F(q (s, v)) ∈{D[v]} и F(q (s, v)) = F(q (s, u)) + A[u, v].

По предположению индукции, F ( q (s, u) ) ∈ { D [ u ]}, а по построению q F ( q (s, v) ) = = F ( q (s, u) ) + A [ u, v ]. Кроме того, известно, что ( u, v ) ∈ G 1 . Отсюда получим F ( q (s, v) ) ∈ { D [ v ]}.

Поскольку { D [ v ]} – множество недоминируемых альтернатив, то в G не может существовать пути из s в v , который доминировал бы над путём q ( s, v ). Следовательно, q ( s, v ) – R -оптимальный путь из s в v .

Отсюда, по индукции получаем, что q – R -оптимальный путь на графе G из s в f .

• 3 этап. Перебор всех путей в построенном графе.

Наиболее простой метод решения этой задачи – алгоритм поиска с возвратом ( backtracking ) [11]. Часто он реализуется в рекурсивной форме. Для задач большой размерности метод не применяется, т. к. он перебирает все возможные решения. Но в данном случае нас интересуют именно все решения, поэтому применение данного метода оправдано. Ниже приведена рекурсивная схема поиска с возвратом всех путей в графе, представленным списками предшествования ПР_Eq [ v] .

Procedure back_tracking(k);

begin for y ∈ ПР_Eq [ x [ k -1]] do

if y = s then write (s, x[k -1]…, x[1]);

else begin x[k]: = y;

back_tracking (k + 1);

end;end;

{Головная процедура поиска с возвратом} begin x[1] : = f;

back_tracking(2);

end.Заключение

Разработан трехэтапный алгоритм поиска в произвольном ориентированном графе всех путей, оптимальных в смысле асимметричного транзитивного критериального отношения предпочтения, в том числе путей, имеющих совпадающие критериальные оценки. Теоретически доказана корректность алгоритма. Проведенные численные эксперименты показали, что предложенный метод эффективно работает на ориентированных графах любого типа в достаточно большом диапазоне размерности. Предложенный алгоритм с минимальными изменениями может быть использован для решения произвольной дискретной задачи динамического программирования.