Показатель работоспособности литейных форм и стержней из синтетических песчаных смесей с учетом физических параметров

Литейная форма, как конструкция, в процессе заливки металлом и формировании отливки испытывает значительные термомеханические нагрузки (большой градиент температур, металлостатическое давление, напряжение усадки и т. д.), которые вызывают различные напряжения и разрушения формы и способствуют возникновению в отливках ряда дефектов.

Литейная форма должна гарантировать качество поверхности, бездефектность (трещины, раковины), массовую и геометрическую точность отливок. После охлаждения отливок в процессе выбивки и очистки формы и стержни должны ра-зупрочняться, обеспечивая низкую прочность и легкость выбивки стержней из отливок и разрушение форм.

При получении отливок в разовых формах из синтетических смесей имеют место две противоположные тенденции: первая – обеспечить параметры смеси по физико-механическим и нормативно-технологическим требованиям в соответствии с регламентом на изготовление отливок при формообразовании и в процессе заливки и охлаждении отливки. Вторая, напротив, обеспечивать разрушение форм и стержней в процессе выбивки и очистки отливок. Эти две противоположные тенденции литейных форм можно прогнозировать, оценивая их термомеханические параметры, как конструкции, способной сопротивляться термомеханическим воздействиям на всех технологических переделах.

Литейная форма со стержнями при заливке сплавом должна быть рассмотрена как квазихруп-кая, сложная иерархически организованная система элементов разных масштабов. Эта система эво- люционирует в процессе заливки и адаптируется к приложенным воздействиям, а ее элементы способны к самоорганизации.

Формы и стержни, независимо от вида связующего, следует считать кластерами с фрактальной структурой, так как их малые элементы являются геометрическими фрактальными объектами, которые обладают свойствами самоподобия, а также масштабной инвариантности, то есть такие, некоторые фрагменты структуры которых повторяются на разных масштабах.

Фрактал (лат. fragere – ломать, разбивать) Fr – геометрическая структура, состоящая из множества точек в n -мерном пространстве, обладающая свойствами самоподобия, дробной фрактальной размерностью и недифференцируемостью. Фрактальная размерность или размерность Хаусдорфа – Безиковича – количественная характеристика множества точек в n -мерном пространстве, показывающая, на сколько плотно точки заполняют подпространство, когда их число становится очень большим [1, 2].

Для синтетических песчаных смесей (СПС) разработана программа для определения фрактальной размерности песков разного генезиса и состава смесей.

Величина Fr позволяет оценить влияние разветвленной поверхности наполнителя на физикомеханические свойства смесей и ее вклад в формирование структуры и показатель работоспособности форм и стержней. Чем больше величина Fr, тем более разветвленная поверхность наполнителя и тем больше площадь адгезионно-когезионных контактов при формировании структуры и прочности форм и стержней. Фрактальная размерность колеблется в зависимости от состава смеси в пределах 1,9–2,7.

В соответствии с кинетической концепцией разрушение твердых тел под воздействием термомеханических нагрузок рассматривается как процесс последовательного разрыва напряженных межатомных связей тепловыми флуктуациями.

Термофлуктуационный разрыв связей обусловлен ангармоничностью тепловых колебаний атомов. Уровень ангармонических межатомных связей количественно характеризуется величиной параметра Gr_L [3, 4].

Ангармонически колеблющиеся атомы и группы атомов вносят существенный вклад в тепловое расширение, в деформацию, теплопроводность, и разрушение твердых тел, особенно при высоких температурах и большом градиенте температур при заливке жидким сплавом.

Сильное различие в потенциалах внутри- и межмолекулярного взаимодействия в связующих приводит к тому, что ангармонизм для межцепных колебаний, которые определяются ван-дер-ваальсовыми связями между цепями, значительно больше, чем внутрицепных, контролируемых ковалентными связями вдоль цепей.

Ангармонизм межмолекулярных ван-дер-ваальсовых сил в большей степени выражен в песчано-глинистых смесях (ПГС), где коэффициент Gr_L изменяется в пределах 9,1–9,4 в зависимости от вида глинистого минерала, меньшая величина соответствует каолиновым глинам, а большая относится к смесям с монтмориллонитовыми глинами. Коэффициент Gr_L для SiO₂ равен 1,8–1,85.

Разрушение форм и стержней при статическом приложении нагрузки в существенной степени связано с концентрацией напряжений около дефектов, случайно распределенных по объему материала. Учет влияния этого фактора на прочность может быть осуществлен количественно на основе статистической теории хрупкой прочности, теории под названием гипотезы «слабого звена» – теории статистической прочности В. Вейбулла [5, 6].

Суть теории в том, что тело (конструкция) считается составленной из большого числа структурных элементов, каждый из которых имеет свою локальную прочность. Предполагается, что разрушение конструкции в целом происходит, когда выходит из строя хотя бы один структурный элемент.

В случае неоднородного напряженного состояния (при наличии градиента напряженности сжатия и растяжения, возникающих в оболочке при завивке металла) разрушение форм (стержней) будет менее вероятно, чем при однородном напряженном состоянии, характеризующимся равенством максимальных напряжений при двух видах напряженного состояния.

Это связано с тем, что область с большими напряженностями занимает лишь часть объема, в то время как наиболее слабый элемент может располагаться во всем объеме случайным образом.

Вероятность Р разрушения конструкции оп- ределяется по уравнению

Р = 1 - exp ( - В ) ,

где В – риск разрушения. В определяют по формуле

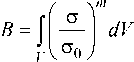
где V – объем растянутой части формы (стержня); ст - локальные напряжения в произвольной точке формы (стержня); ст0 - константа смеси, имеющая размерность напряжения; m – показатель, учитывающий неоднородность прочностных свойств смеси в различных участках формы или стержня.

Чем меньше m , тем больше неоднородность прочностных свойств смеси и влияние градиента напряжений на прочность формы (стержня). Зная распределение напряжений в форме (стержне) можно определить B , а затем найти математические ожидания предела ее прочности:

ст B = j e ^- B d ст . (3) 0

С учетом фрактальной размерности наполнителя смесей Fr, коэффициента неоднородности прочностных свойств смесей m в различных участках формы (стержня) и параметра Грюнайзена GrL получены выражения для определения показателя работоспособности (эксергии) Rb литейных форм и стержней из синтетических песчаных смесей.

Для оболочковой формы на связующем – син- тетические смолы и кварцевом песке получено выражение Rb:

1 m

^ст ВР

V p

2 ^П h пр J

Ф ( r = b )ln Fr

Rb оболочковая форма

CTfl Ф     + ст’ и0 (r=b)      umax p lg GrL =

^ст ВР

V p

^{2 n} h пр J

1 m

ln Fr

ст^, ста +p

И0 rh

^Ф( r = b )

lg Gr L =

1 m

Vp ho (2 a + ho)    . _ стВР —---------- In Fr lgGrL, (4)

Антошкина Е.Г., Смолко В.А.

внесены соответствующие изменения и получено уравнение:

Rb = форма из ПГС

ств Всж

- 1 сж2 ( m + 1 )( 2 m + 1 )

1 m ln Fr

^-|р gh

аЕ (To - T)

lg Gr L ,     (5)

, h 1 b

2 1 1 -v ln —

I a

где cB  - предел прочности смеси при неодно- cж родном сжатии, рассчитанный из рассмотрения состояния смеси, соответствующее трехточечному изгибу, МПа.

Показатель работоспособности Rb сплошного стержня определяется из выражения

Rb = сплошной стержень

° ВР

^{3 (} m + 1 ) V p h o ^{( 2} b ^- h o ) T m

V ЗИ b ²

аЕ (Тo — Тi)

4 (1 -v)

^-|р gh|

ln Fr

lg Gr_L ,    (6)

где ст _ВР - предел прочности смеси при разрыве, МПа.

Для оболочкового стержня показатель работоспособности Rb рассчитывается в данном случае по уравнению

° ВР

Rb оболочковый стержень

^а ВР

V p

^{2 п} h пр J

^A

^U 0

—

V p

^{2 п} h пр J

1 m

^Ф( r = a )^ln Fr

аА Ф и0    (r=а)

- |о‘ max с

lg Gr L =

1 m

ln Fr

а‘„ max с

lg Gr L =

Ф, A

( r = a )

° ВР

V p h o ( 2b - h o )

2 V ЗИ J

1m ln Fr

x

а Е ( T o - T ) 2 ( 1 -v ) ln b a

2 p ghb ²

I i i b a 2 + b 2i b I ( b - a ) - 1 + ln- + --- _Tln- ^v ( a b ² - a ² a J

x lg Gr L , (7) где V _p – объем рабочей части, м³; m – показатель, учитывающий неоднородность прочностных свойств смеси в различных участках формы (стержня); Fr – фрактальная размерность; Gr_L – коэффициент Грюнайзена; p - плотность, кг / м³; а - коэффициент линейного расширения смеси, град^–1; Е – модуль

упругости смеси, МПа; h 0 – высота сечения образца, м; v - коэффициент Пуассона; а - внутренний радиус оболочковой формы, м; b – внешний радиус, м; V _ЗИ – объем рабочей части образца при трехточечном изгибе, м³; Т 0 – температура на внутренней поверхности оболочки, К; Т 1 – температура на внешней поверхности оболочки, К.

Для расчета показателя работоспособности оболочковых форм и стержней на смоляных связующих, а также для стержней и форм из ПГС разработана программа Sint exe.

Показатели работоспособности должны быть в пределах Rb 1,5–3,0 в зависимости от конструкции формы и стержня , что обеспечит изготовление форм и стержней и предотвратит их разрушение в процессе транспортировки на конвейерах, рольгангах и других транспортных операциях и будет гарантировать получение качественных отливок.

Разработанная методика оценки служебных свойств форм (стержней) с учетом фрактальной размерности, ангармонизма и неоднородности прочностных характеристик смесей, позволяет на стадии инженерных расчетов, разработки технологического процесса формообразования и заливке, установить показатель работоспособности формы, как конструкции. Определить оптимальный состав синтетической смеси для форм и стержней, толщину оболочки формы (стержня), в случае отверждения их в оснастке и в зависимости от вида сплава, температуры заливки и геометрических параметров, прогнозировать возможность получения качественных отливок в формах, выдерживающих термомеханические напряжения в процессе заливки их металлом, формирование отливки и в дальнейшем разупрочнение смесей при выбивке и очистке отливок.