Показатели асимметрии в задачах изучения поведенческой активности пользователей продукта

Современное состояние исследований социально-экономических систем представляет собой процесс взаимного проникновения концепций, принципов, моделей и методов из смежных наук, что расширяет возможности для понимания явлений, происходящих в мире природы и человека [1, 2]. В условиях цифровизации рыночной экономики особую степень важности и актуальности приобретают задачи построения прогностических моделей эволюции рынков товаров и услуг, основанные на изучении поведения потребителей. Разумеется, принятие решений по развитию продуктов, позиционированию их

ГРНТИ 06.35.51

Алексей Николаевич Кисляков – кандидат технических наук, доцент, доцент кафедры информационных технологий Владимирского филиала Российской академии народного хозяйства и государственной службы при Президенте Российской Федерации.

Статья поступила в редакцию 03.04.2020.

на рынке, брендированию и т.п. должно сопровождаться не только маркетинговыми исследованиями, но и более обширными исследованиями состояния рынков на предмет стабильности развития.

В этой связи, целю работы является разработка методики оценки устойчивости функционирования рынков товаров и услуг на основе результатов анализа поведенческой активности пользователей продуктов. Разработанная методика позволяет создавать математические модели и автоматизированные интеллектуальные системы поддержки принятия решений в целях повышения эффективности ведения хозяйственной деятельности в изменяющихся условиях.

Материалы и методы

Наиболее распространенными на сегодняшний день являются регрессионные прогностические модели, лежащие в основе большинства моделей интеллектуального анализа данных и машинного обучения, при создании которых возникает необходимость математического описания модели на основе обучающей выборки с большим количеством признаков-факторов и апробации созданной модели на основе тестовой выборки. Однако, зачастую возникают ситуации, когда при выполнении регрессионного анализа поведения клиентов модель хорошо работает на тестовой выборке, но показывает неудовлетворительные результаты на тестовых данных даже при кросс-валидации.

В этом случае сложность состоит не в переобучении модели, а в том, что в тестовой выборке существуют неочевидные закономерности, которые не учитываются при построении модели. Избежать данной ситуации позволяет ряд методов, таких как, например, ковариативный сдвиг, удаление смещенных признаков [3] и т.д. Однако, в большинстве случаев индикация и интерпретация именно этих закономерностей позволяет не только оценить качественные характеристики построенной модели, но и выявить основные направления развития продукта и отношения покупателей к нему, а также оценить устойчивость рынка продуктов с аналогичными характеристиками на основе изучения поведенческой активности его участников. При этом, реакция покупателей может зависеть от множества случайных факторов, нарушая баланс интересов участников рыночных отношений [4]. Это явление называется информационной асимметрией, и выражается в разной степени информированности групп «продавцов» и групп «покупателей» – пользователей продукта о состоянии рынка, что определяет различные поведенческие настроения и намерения участников рынка [5, 6].

Методы изучения явления информационной асимметрии [7] в контексте случайной изменчивости в поведении участников взаимодействия социально-экономической системы тесно связаны с вопросами изучения эволюционных процессов в биологических и природных системах, начиная с работ К. Присона, который изучал фундаментальные основы изменчивости в математических регрессионных моделях, до более поздних прикладных исследований в кристаллографии, где были разработаны метрики для оценки характеристики псевдосимметрии кристаллов, и целого ряда работ по биостатистике [8, 9], раскрывающих вопросы устойчивости эволюционных процессов на основе показателей асимметрии признаков биологических особей [10].

Однако математического аппарата теории статистики и возможностей построения и анализа регрессионных моделей в этом случае недостаточно. Теория графов в этом смысле обладает более обширными возможностями с точки зрения описания механизмов возникновения асимметрии, а также возможностей визуализации процессов. Одним из ключевых показателей, характеризующих явление нарушения симметрии в социально-экономических, живых и природных системах является флуктуирующая асимметрия [8,9]. Применительно к социально-экономическим системам асимметрия представляет собой случайные отклонения от устойчивого состояния системы, вызванные неспособностью эволюции социально-экономического системы точно следовать «программе», заложенной в экономической модели. Существуют показатели асимметрии [9], которые используются для характеристики стабильности развития системы и характеризуют степень вариативности (изменчивости) развития процесса в пределах нормы реакции системы.

В биостатистике реализационной изменчивостью характеризуются отличия между разными результатами реализации одной и той же наследственной программы [10]. Механизмы эволюции живых и социально-экономических систем в этом смысле схожи, ввиду того, что биологические, природные и социально-экономические системы являются открытыми, динамическими и стохастическими [11]. Поэтому при анализе асимметрии необходимо учитывать степень изменчивости признаков внутри групп элементов системы: так, модель взаимодействия участников рынка зависит от условий реализа- ции одной и той же экономической модели в различных изменяющихся условиях. В благоприятных условиях внешней среды система развивается симметрично относительно всех субъектов взаимодействия – участников рынка, т.е. наблюдается симметрия и однородность признаков при описании процесса. Эта симметрия может быть выявлена при сравнении признаков внутри гр упп элементов системы на основе тестовой и обучающей выборки для регрессионной модели, путем сравнения на основе интегрального показателя симметрии.

Следует отметить, что относит е льно груп п элементо в системы и механизм о в их взаи м одействия симметрия м ожет быть двухсторо н ней, центр а льной, тра н сляционно й , функцио н альной и т .д. и зависит от контекста использования да н ного дово л ьно широк о го поняти я . Мы в дан н ой работе с осредоточимся на формах проявления асим м етрии при наблюдении двух вар и антов разв и тия одног о и того же процесса (р и сунок 1), что является н еобходим ы м при исс л едовании качества рег р ессионны х моделей.

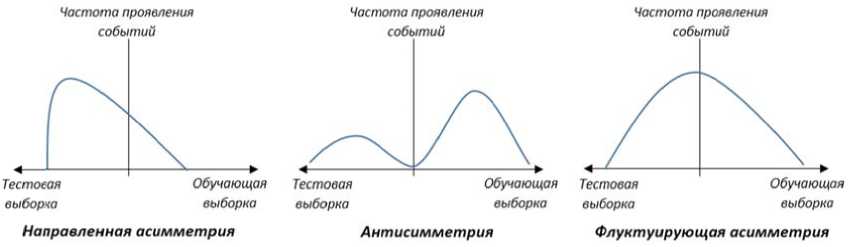
Р и с. 1. Формы проявления асимметрии

При рассмотрении указанных форм прояв л ения асим м етрии при м енительно к моделям в заимодействия участ н иков рынка очевидно, что в случ а е направле н ной асимм е трии реги с трируется п реобладание определ е нных признаков сдел к и только в одной из г рупп собы т ий. Это ха р актерно в случае неверного раз б иения всего множеств а событий н а тестовую и обучаю щ ую выбор к у. В случа е антисимметрии мог у т встречаться как отк л онения в с т орону тес т овой, так и в сторону обучающей выборки, и эти откло н ения встречаются ча щ е, чем одн о родное состояние пр и знаков вза и модейств и й. Это характерно дл я моделей «власти пр о давцов» и л и «власти покупателе й » [7], когд а наблюдается дисбаланс в отношениях участников рынка, описа н ие призна к ов которы х выходит з а рамки п о строенной модели, т.е. и меются скрытые факт о ры, оказы в ающие влияние на пр о цесс и не у ч тенные в м одели.

Наконец, в случае флуктуирую щ ей асимм е трии наиб о лее часто н аблюдаетс я и преобл а дает явление устойч и вого однородного сос т ояния при з наков сде л ок в тестовой и обу ч ающей вы б орке, при э т ом сильн ы е отклонения встреча ю тся горазд о реже, чем слабые. Та к им образо м , чем мень ш е показатель асимметрии, тем устойчивей р азвитие си с темы, чем у способств у ют: благо п риятные у с ловия развития бизне с а, здоровая конкурен т ная среда; « гибкость» социально - экономиче с ких услов и й ведения хозяйственной деятельности, кото р ая выража е тся в сбалансированн о сти бизне с -процессов; устойчивые механиз м ы регулирования отк л онений кл ю чевых показателей эффективнос ти бизнеса.

Для оце н ки показателя асимметрии исполь з уется след у ющее выр а жение [10] :

2 _ 2i=i^(di-t^-Md ) _ Sz=i d ;-t л _ ^2(d i ^-d t ) a , Ma , ^1 , ^d n-1 ^d n ^{1 L} d i +d t

где ad - показатель асимметрии, который рассчитывается как дисперсия различий между выборками относительно среднего различия; dz и dt - значение признака для обучающей и тестовой выборки; Ма -среднее различие между выборками по всем показателям; n – общее количество измерений.

Таким образом, с помощью по к азателя ас и мметрии о ц енивается с тепень отк л онения от с реднего в р я ду закономерно повторяющихся реакций с и стемы. Однако, разли ч ные групп ы элемент о в, объединенные общими признаками (клас т еры), могу т вести себя по-разно м у [12, 13]. Х арактеристики взаимодействия кластеров могут быт ь визуализ и рованы с и спользова н ием напр а вленного графа [14]. В этой связи случайная изменчиво с ть морфол о гических признаков социального г рафа взаи м одействия повышается при отклонении от ус л овий опти м ума и/или появлении большего к оличества с лучайных факторов [15].

Результаты и обсуждение

В качест в е примера рассмотри м возможно с ть кластеризации баз ы данных, с о держащей признаки поведенчес к ой активности клиент о в. Выборк а состояла и з ста клие н тов (n = 1 0 0) и неско л ьких признаков. Дан н ая выборка состоит и з идентиф и катора клиента и нес к ольких по к азателей п о каждому из признако в , характеризующих с д елки с эти м клиентом. Каждый из этих кли е нтов являе т ся вершиной сетевого г рафа, а связи между э тими вер ш инами характеризуют с я мерами с хожести с д елок каждой пары клиентов. Методика оценки устойчив о сти структуры взаимо д ействия м е жду участ н иками рынка с использ о ванием показателя ас и мметрии в к лючает ря д этапов.

На пе р вом этапе выполняется разбиени е выборки на тестовую и обучаю щ ую (в каждой по 50 клиентов с векторами признаков сд е лок). Зате м выполняется кластер и зация тест о вой и обу ч ающей выборок на основе иерархических ме т одов, реал и зующих следующие в а рианты об ъ единения [ 14]:

• 1.    Агломеративная кластери з ация начи н ается с n к л астеров, гд е n — числ о наблюден и й: предполагается, ч т о каждое из них пред с тавляет со б ой отдель н ый класте р . Затем ал г оритм пыт а ется найти и сгруппир о вать наиболее схожие между соб о й точки данных; так н а чинается ф ормирован и е кластеров.

• 2.    Ди в изионная кластеризац и я выполн я ется противоположным образом: изначально полагается, что все n точек данных предста в ляют собо й один бол ь шой класт е р, а далее н аименее с х ожие из них разделяются на отдельные груп п ы.

Результаты кластеризации в виде денд р ограмм [1 4 , 16] показ а ны на рис у нке 2, а ха р актеристики качества итеративного процесса разбиения н а кластер ы указаны в т аблице.

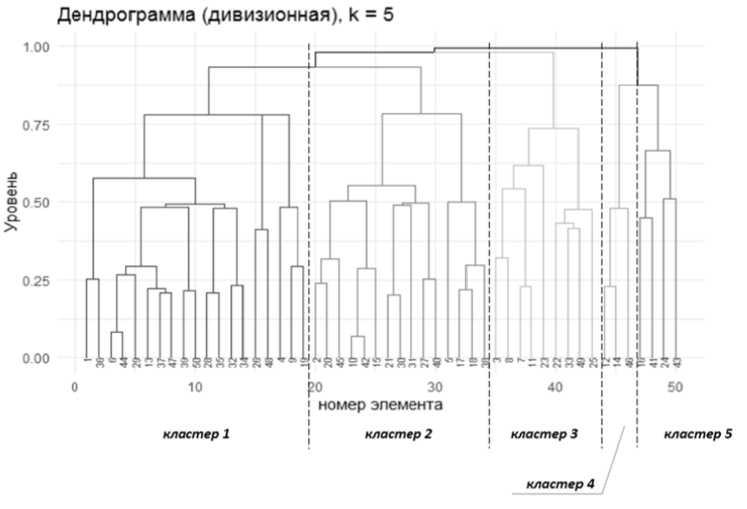
Рис. 2. Прим е р иерархиче с кой кластеризации диви з ионным ме т одом

На следующем этапе рассч и тывается п оказатель асимметри и в соответ с твии с выражением (1) между те с товой и обучающей в ы борками п о каждому из признак о в. Для оце н ки вариат и вности показателя асимметрии необходимо в ыполнить с равнение е го значени й для разли ч ного количества кластеров (рисунок 3). Следует отмет и ть, что по к азатели ас и мметрии р ассчитыва л ись после у порядочения как тесто в ой, так и обучающей выборок п о результатам дивизио н ной и агл о меративно й кластеризации.

Из рисунка 3 видно, что порядок значений показателя асимметрии в обоих случаях схож и составляет 5,5-6,0 % для сравниваемых алгоритм ов иерархической кластеризации, однако в случае агломе-ративной кластеризации наблюдается незначительное снижение показателя асимметрии до 4,0-4,5% для 4-6 кластеров. Это объясняется тем, что в соответствии с результатами и сследований [17] именно такое количество кластеров оптимально для разбиения данной выборки и более ярко выражено для алгоритма агломеративной кластеризации. Для оценки оптимального количества кластеров использовались следующие показатели: сумма квадратов расстояний между объектами внутри кластера и средняя ширина силуэта [13, 17]. В этой связи показатель асимметрии может быть полезен не только при оценке однородности выборки, но и при оценке оптимального количества кластеров [18].

Таблица

Характеристики качества процесса кластеризации

Показатель	Т ип выборк и
	обуча ю щая выбор к а				т естовая вы б орка
номер итерации разбиения	2	3	4	5	2	3	4	5
количество э лементов в выборке n	50	50	50	50	50	50	5 0	50
	Дивизи о нная класте р изация
сумма квад. р асст. между наблюд. в класт.	9,51	7, 4 6	5,94	5,30	10,2 0	8,22	7,47	6,23
сред. расст. м ежду наблюд. внутри к л аст.	0,60	0, 5 4	0,49	0,47	0,63	0,57	0,54	0,50
среднее рас с тояние между кластерам и	0,75	0, 7 4	0,70	0,70	0,74	0,73	0,72	0,71
средняя ши р ина силуэта	0,19	0, 2 3	0,22	0,24	0,15	0,19	0,16	0,19
количество э лементов в кластере № 1	43	34	19	19	40	18	1 0	10
количество э лементов в кластере № 2	7	9	15	15	10	22	2 2	16
количество э лементов в кластере № 3	0	7	9	9	0	10	8	8
количество э лементов в кластере № 4	0	0	7	3	0	0	1 0	6
количество э лементов в кластере № 5	0	0	0	4	0	0	0	10
	Агломе			р а тивная клас т е		ризация
сумма квад. р асст. между наблюд. в класт.	9,64	8,15	6,54	5,88	9,15	8,44	7,52	6,36
сред. расст. м ежду наблюд. внутри к л аст.	0,61	0, 5 5	0,51	0,49	0,59	0,57	0,54	0,50
среднее рас с тояние между кластерам и	0,67	0, 6 7	0,68	0,69	0,74	0,73	0,73	0,73
средняя ши р ина силуэта	0,09	0,11	0,15	0,16	0,20	0,16	0,16	0,19
количество э лементов в кластере № 1	21	21	13	13	24	24	2 4	24
количество э лементов в кластере № 2	29	20	20	20	26	11	7	7
количество э лементов в кластере № 3	0	9	9	9	0	15	1 5	9
количество э лементов в кластере № 4	0	0	8	6	0	0	4	6
количество э лементов в кластере № 5	0	0	0	2	0	0	0	4

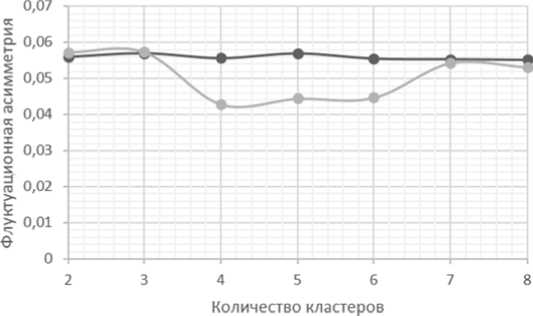
—•—Дивизионная кластеризация —•— Агломеративная кластеризация

Р и с. 3. Результаты расчета показателя а симметрии д ля различного количест в а кластеров

Кроме того, исследования показали, что при неверной интерпретации кластеров в тестовой и обучающей выборке показатель асимметрии может как увеличиваться, так и снижаться, что дает возможность оценить правильность интерпретации признаков групп разбиения. Однако, для определения формы про- явления асимметрии необходимо провести дополнительное исследование изменения значения показателя асимметрии при различных вариантах разбиения групп на кластеры. Резул ьтаты таких экспериментов, проведенных с использованием метода Монет-Карло [19] для 5 кластеров приведены на рисунке 4 в виде статистической гистограммы распределения вероятностей появления различных значений показателя асимметрии. Случайное переупорядочение выполнялось для тестовой выборки.

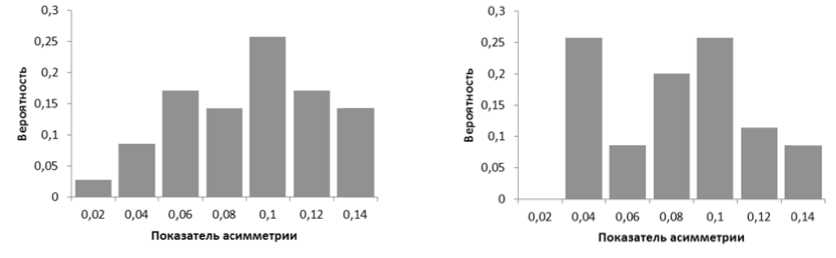
а                                            б

Рис. 4. Функция плотности вер о ятности рас п ределения показателя ас и мметрии п р и различны х вариантах разбиения тестовой и обучающе й выборок д л я случая дивизионной (а) и агломера т ивной (б) кл а стеризации

Функции плотности вероятн о сти распр е деления показателя ас и мметрии п ри различных вариантах разбиени я тестовой и обучающей выборо к , показанн ы е на рису н ке 4, позв о ляют сдел а ть выводы о форме п р оявления асимметри и : в случае дивизион н ой класте р изации на б людается н аправленная асимметрия в сторону увеличе н ия значен и я показате л я асиммет р ии, получ е нного при р азбиении на 5 кластер о в, равного 0,057. Это о значает, ч т о результа т кластериз а ции позво л яет улучш и ть разбиение выборок, снизив при этом показ а тель асим м етрии.

В сл у чае агломеративной к ластеризац и и наблюд а ется случ а й проявле н ия антиси м метрии, при этом зна ч ения показателя асим м етрии, пол у ченное пр и разбиении на 5 класт е ров, равно е 0,044 совпадает с од н им из наиболее вероя т ных интер в алов значе н ий показателя асимме т рии, но су щ ествует еще один инт е рвал значений показателя асим м етрии, в к о тором вер о ятность и м еет практи ч ески схожее значение и данный интервал так ж е смещен в сторону увеличения з начения п ок азателя ас и мметрии.

В слу ч ае наиболее рациона л ьного раз б иения дол ж на наблю д аться флу кт уирующа я асимметрия, значение показателя которой б у дет совпа д ать с инте р валом, им е ющим наи б ольшую в е роятность, и функция р аспределения вероят н остей буде т иметь си м метричный вид. Резул ь таты иссл е дований позволяют с д елать следующие выв о ды:

• 1.    По к азатель асимметрии п р и однород н ой выборке остается о тноситель н о стабиль н ым при качественной кластеризации массив а данных п о нескольки м признака м .

• 2.    Фл у ктуирующая асиммет р ия наблю д ается при н аиболее р а ционально м варианте разбиения на кластеры при сбалансированны х однородн ы х выборках, но на практике встр е чается дос т аточно редко и являетс я наиболее идеальным случаем.

• 3.    По к азатель асимметрии п о зволяет оц е нить качес т во кластер и зации и в ы явить фор м у нарушения симметр и и в выборках, а также п ри оценке о птимальн о го количес т ва кластер о в.

• 4.    Раз р аботанную методику следует пр и менять в целях повы ш ения эфф е ктивности разработки и примене н ия регрессионных мод е лей и алго р итмов кла с теризации.

• 5.    Ис с ледованные свойства показателя асимметрии позволя ю т сделать в ывод о п о лезности его примене н ия в целях оценки устойчивости с труктур в з аимоотношений на р ы нке товаро в и услуг при анализе р е зультатов кластериза ц ии потреб и телей по вектору приз н аков.

Заключен и е

Наиболее актуальная проблема исследований эволюционных процессов на р ынках товаров и услуг в условиях цифровизации, безусловно, требует исследования не только поведенческой активности пользователей продукта, но и исследования другой стороны процесса – анализа популярности групп продуктов по признакам. Разработанная методика позволяет решить и такую задачу, а математиче- ский аппарат статистики и теории графов обладает универсальными подходами, позволяющими решать задачи на стыке многих областей знаний и более эффективно применять регрессионный и кластерный анализ для исследований явлений в сложных системах и создания математических моделей описания процессов, протекающих в них.

Благодарности

Исследование выполнено при поддержке гранта Российского фонда фундаментальных исследований (РФФИ) № 18.07.00170.