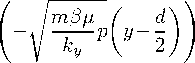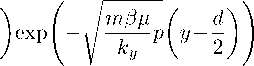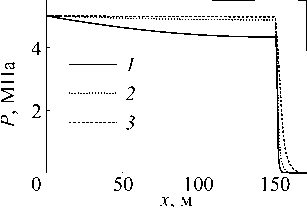Поле давления в пласте с трещиной гидроразрыва конечной длины
Автор: Филиппов А.И., Давлетбаев А.Я., Гареев Р.Р., Губайдуллин М.Р.
Журнал: Вычислительная механика сплошных сред @journal-icmm
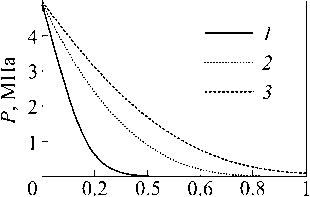
Статья в выпуске: 1 т.18, 2025 года.
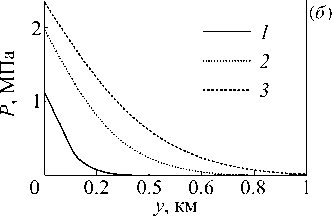
Бесплатный доступ
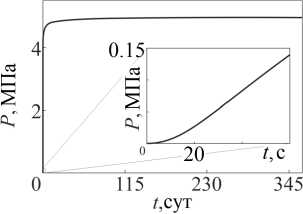
На основе аналитико-численного подхода исследовано поле давления в слоисто неоднородном идеально перфорированном пласте при плоском течении жидкости к вертикальной трещине гидроразрыва. Информация о поле давления имеет важное значение для нефте- и газодобычи, гидрогеологии, совершенствования технологии извлечения углеводородного сырья из нефтяных и газогидратных месторождений путем закачки химически активных или радиоактивных растворов. Для построения аналитического решения в главном приближении использован асимптотический метод. Приведено решение задачи для случая, когда в области влияния на состояние породы нагнетательных скважин в окрестности вершины трещины поддерживается критическое давление, соответствующее при некоторых условиях ее самопроизвольному росту. На основе алгоритма численного обращения изображений Лапласа-Карсона создана программа и осуществлены расчеты пространственно-временных распределений давления в трещине и окружающей породе-коллекторе. Показано, что перепад давления в трещине сравнительно быстро становится близким к давлению нагнетания, а градиент давления стремится к нулю. При этом основные изменения давления в направлении развития трещины сконцентрированы в зоне, размеры которой существенно меньше размеров зоны возмущений, ориентированной поперек трещины. Установлено, что в коллекторе градиенты давления по пути продвижения трещины намного больше градиентов в боковых по отношению к трещине областях пласта. Вследствие этого создаются благоприятные условия для роста трещины. Представленные результаты позволяют определить время достижения в вершине трещины критического давления, при котором начинается процесс автогидроразрыва.
Фильтрация, поле давления, трещина автогидроразрыва, асимптотический метод
Короткий адрес: https://sciup.org/143184125
IDR: 143184125 | DOI: 10.7242/1999-6691/2025.18.1.1
Текст научной статьи Поле давления в пласте с трещиной гидроразрыва конечной длины
Наблюдение за эволюцией месторождений нефти и газа в процессе длительной эксплуатации представляется весьма важным для оптимизации процесса добычи и учета полученных сведений при разработке новых продуктивных горизонтов как для повышения эффективности извлечения углеводородов, так и для избегания/устранения возникающих экологических проблем [1, 2] . Необходимость мониторинга все более осознается в процессе накопления фактической информации, анализ которой порождает новые теоретические задачи [3] .
Одна из таких задач заключается в изучении искусственных и естественных трещин в процессе освоения месторождения. Неконтролируемое развитие трещин существенно изменяет условия в породном пласте и влечет за собой экологическую опасность, особенно при добыче сланцевого газа из сравнительно неглубокозалегающих пластов.
Результаты исследования месторождений свидетельствуют о возможном появлении трещин в пространстве между нагнетательными и эксплуатационными скважинами. Процесс получил название автогидроразрыва пласта (автоГРП) [4, 5] . Главной причиной образования трещин является величина давления в нагнетательной скважине, необходимая для поддержания достаточно высокого уровня пьезопроводности — способности пласта-коллектора передавать давление. Присутствие трещин приводит к обводнению эксплуатационной скважины и уменьшению количества нефти в продукции при ее достаточно высоком содержании в зоне разработки. Таким образом, детальное изучение процесса автоГРП позволит понять причины и условия его возникновения и развития.
При этом важное место отводится задачам фильтрации, которые в рассматриваемом случае осложнены необходимостью учета как наличия трещин, так и возможности их продвижения. Задачи с подвижными границами являются нелинейными даже при использовании линейных уравнений пьезопроводности, а их решение и численная реализация сталкиваются со значительными трудностями.
Решение задач фильтрации такого рода требуется для совершенствования главного подхода к исследованию трещин автоГРП [6, 7] — трассерных технологий, которые основываются на растворении в закачиваемой в пласт воде специальных добавок (трассеров) и последующем измерении их концентрации в продукции соседних добывающих скважин. Улучшение интерпретации данных измерений побуждает к решениям задач конвективной диффузии, в которых важнейшим этапом является определение полей скорости фильтрации, возникающих от действия полей давления.
В данной статье решается задача нахождения поля давления в пласте-коллекторе с трещиной конечной длины. При этом учитывается возможность роста трещины при достижении критического давления P A в окрестности ее вершины. Отметим, что представления о критическом давлении, основанные на экспериментальных исследованиях и численном моделировании, позаимствованы из работы [8] .
Построение аналитического решения задачи потребовало модификации асимптотического подхода, возможности которого пока мало реализованы в теории фильтрации. Асимптотические методы исторически
Статья опубликована в открытом доступе по лицензии CC BY 4.0
послужили основой многих открытий в области небесной механики и практически во всех разделах физики, а также активно развивались математиками [9 –14] . Примерами успешного применения асимптотических методов авторами данной статьи могут служить задачи сопряжения математической физики (см. публикации [15 –19] ).
Используемый здесь подход включает: дополнение задачи асимптотическим параметром, полученным из физических соображений; последующее представление параметризованной задачи в виде бесконечной последовательности задач для коэффициентов асимптотического разложения, решение которых может быть найдено хорошо известными методами, например, методом интегральных преобразований.
-
2. Постановка задачи
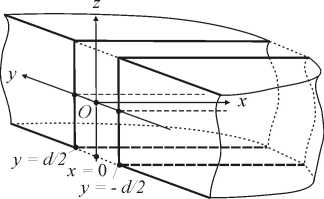
Рис. 1. Ближняя к скважине зона горизонтального пласта с вертикальной трещиной гидроразрыва, локализованной в слое ( - d/2)
На рисунке
1
показана ближняя к скважине зона горизонтального пласта с вертикальной трещиной гидроразрыва:
(
-
d/2)
На рисунке 2 схематически изображена геометрия задачи фильтрации в направлении трещины гидроразрыва, имеющей толщину d и конечную длину L и расположенной около ствола нагнетательной скважины. Трещина окружена проницаемой средой, в которую осуществляется закачка жидкости для поддержания заданного давления. Среда имеет такие же характеристики, как реальный пласт-коллектор.
|
.У п У = d/2 |
Л |
( б ) |
|||
|
t У = dft |
p. |
( а ) |
|||
|
x = 0 P |
X |
x = 0 P |
X |
||
|
x = L |
x = L |
||||
|
у = - d/2 |
у = - d/2 |
||||
Рис. 2. Геометрия задачи фильтрации в пласте с трещиной гидроразрыва переменной длины L в горизонтальном сечении пласта ( а ) и вспомогательная геометрия для построения аналитического решения ( б )
Предполагается, что в системе выполняются условия глобального термического и химического равновесия. Вследствие этого, как известно [13, 15] , для исследования глобальных неравновесных механических процессов применима теория нестационарных физических полей давления, в рамках которой фильтрующаяся жидкость не обладает аномальными свойствами, является ньютоновской, а скорость фильтрации и градиент (изменение на единицу длины) давления связаны законом Дарси для анизотропной среды. При таких допущениях движение жидкости описывается уравнением пьезопроводности, вывод которого приводится в [1, 2] .
Условия формирования осадочных пород способствуют возникновению анизотропии [1, 2] , причем проницаемость вдоль пласта чаще всего намного превышает поперечную. Процесс закачки в трещину гидроразрыва гранулообразного материала (пропанта) приводит к анизотропии проницаемости. Принято допущение, что компоненты тензора проницаемости и сжимаемость сред не зависят от величины давления. Учет анизотропии в рассматриваемой задаче предоставляет дополнительные возможности для исследования течений с сильно отличающимися значениями градиента давления в различных направлениях. Для упрощения задачи предполагается также, что пористая среда и трещина обладают трансляционной симметрией по оси Oz .
Необходимо найти поля давления P(x,y,t) в трещине, заполненной пропантом, и P 1 (x,y,t) в окружающем слое-коллекторе. Его свойства — компоненты проницаемости, пористость и вытесняющую способность, соответственно, обозначим как k x , k y , m , β .
Математическая постановка задачи фильтрации к трещине гидроразрыва (Рис. 2а ) включает уравнение пьезопроводности с компонентами тензора проницаемости k px , k py , пористостью m p и вытесняющей способностью β p :
∂P1 ∂2P ∂2P mpвр ^~дГ -kpx dX2 - ky W =0,
t>
0, 0
В расчетной области задачи ft = {t>0, 0 ∂P1 ∂2P1 '■ - kx ^ - ∂2P1 ky Л 2 0. ∂y2 На входе в трещину задаем давление Pw : . . dp. Plx=0 = Pw, (-d/2 = 0, |y| > (d/2). ■=0 На остальных границах S трещины принимаем условия равенства давлений и фильтрационных потоков: P |S = P1|S, — kpy Ъ s , dPi y дУ s ’ В начальный момент времени возмущения давления отсутствуют, а величину естественного гидростатического давления берем за отсчетную: P lt=o = 0, Pilt=o = 0. (5) Для построения аналитического решения область Ω разбиваем на три подобласти (Рис. 2б). Вводим обозначение Pa для поля давления в подобласти Q2 = {t>0, x>L, (-d/2) Рассматриваемая задача является симметричной относительно линии у = 0. Ее математическая постановка существенно упростится, если принять во внимание условие симметрии: ∂P ∂y = 0, y=o ∂Pa ∂y = 0. y=o Тогда можно ограничиться построением решения только в квадранте положительных значений x и y . Решение задачи отыскиваем в виде асимптотических разложений по формальному параметру ε: P = P(0)+eP(1)+...+enP(n)+ 6(n\ Pa = Pi0 + eP^ + ...+EnPa(n)+0^, (7) Pi= Pi0+eP11 +...+enPin + 0(n1. Для реализации асимптотического метода параметризуем задачу (1)–(6) путем замены kpy и kay величинами kpy/e и kay/e как в уравнении (1), таки в граничном условии (4). Этим обеспечиваем построение решения для усредненного по сечению трещины поля давления в нулевом (или главном) асимптотическом приближении [16–19]. В частных случаях найденные таким образом решения совпадают с построенными по «схеме сосредоточенной емкости», которая широко используется в реальных расчетах [15]. Поперечные размеры трещины гидроразрыва чаще всего имеют порядок ~10-2 м, поэтому для практических целей достаточно определять усредненное поле давления. Это позволяет ограничиться построением только главного приближения задачи. Тогда формулировка задачи в симметризованной и параметризованной постановке приобретает вид: ∂P mpβp µ ∂t - k d2P :px dx2 ∂Pa mβµ - k ∂t ax dPi и mβµ ∂t - kx d2Pa dx2 d 2Pi dx2 kpy d2P = e dy2 kay d2Pa 0, t> 0, 0 0<у< (d/2), e dy2 , d2Pi kydy2 = 0, = 0, t> 0, t> 0, x>L, 0 <у< (d/2), 0 P\x=o = Pw , 0 dPi ∂x = 0, |y| > (d/2), P \y=(d/2) = P1|y=(d/2), kpy∂P ε ∂y y=(d/2) = ky x=o dPi ∂y , t> 0, 0 Pa ly=(d/2) = Pi|y=(d/21, kpy ε ∂Pa ∂y P\x=L = Pal px ∂P ∂x P\t=o = 0, ∂P ∂y =k y=(d/2) dPa — kax q ox „ Pa|t=o = 0, y=o = 0, ∂Pa ∂y dPi y ∂y y=(d/2) , t> 0, x>L, , t> 0, Pi\t=o = 0, = 0. y=o 0 3. Асимптотическое представление задачи После подстановки (7) в (8) и несложных преобразований получаем: kpy d2P(0)n dP(0) , d2P(0) , d2P(1) A 9 + mp вр ' 91 kpx A 9 kpy й 9 + s dy2 dt dx2 dy2 +e(mpPpM^kpxddP2kpy''P^ )+- =0 Выражение (17) содержит коэффициенты асимптотических разложений (7) и позволяет построить уравнения для их отыскания. Например, для устранения сингулярности порядка 1/s приходим к уравнению: d2P(0)/ду2 = 0. Аналогичная подстановка асимптотических формул в (12) и (13) приводит к граничным условиям для производной нулевого коэффициента асимптотического разложения: I dP(0)/ду ) I =0 и ( дР(0)/ду ) I =0.Найденному \ / Iy=L \ J ly=0 уравнению и граничным условиям, как нетрудно видеть, удовлетворяют только решения, не зависящие от координатыу: Р(0)= Р(0)(x,t). После осуществленного выше устранения сингулярности минус первого порядка из (17) имеем уравнение для нулевого порядка ε: mp^M^Pt—kpx ^P—kpy ^P-=0, связывающее нулевой и первый коэффициенты асимптотического представления искомого поля давления. Такие уравнения в асимптотических разложениях называются зацепленными. Воспользуемся процедурой расцепления, заключающейся в следующем. Интегрируем уравнение (18), учитывая, что P(0)(x,t) не зависит от у: дР(1) kpy ∂y mpβpµ дР(0) ∂t px д2Р (0)\ я 2 ) y + C. дх2 ) Константу интегрирования C находим из условия ( дР(1)/ду] I = 0, следующего из (16): C = 0. Далее \ I y=0 с помощью равенства kpy (дР(1)/ду}I = ky( дР^/ду] I , вытекающего из (13), получаем ' ' ।y=W2) ' ly=(d/2) расцепленное уравнение для нулевого коэффициента: n дР(0) , д2Р(0) 2kyдР(} mp^'^t kpxдх2 = “d" ду Заметим, что правая часть уравнения (20) содержит след производной из внешней области. Уравнение (20) применимо в интервале 0 (0) 2 (0) (0) YLaь. д Ра 2ky дР1 flip' kax а 9 — 1 а дt дх2 d ду . y=(d/2) Построение аналитических выражений для нулевого коэффициента асимптотического приближения имеет большое практическое значение, так как получаемые приближения составляют главную часть поля давления. Поэтому особую ценность имеют те асимптотические представления, в которых значения первого коэффициента вносят лишь небольшую поправку. Сравнения, убеждающие в этом, чаще всего выполняются на основе вычислительных экспериментов в интересующем диапазоне параметров. 4. Главное приближение Построение остальных уравнений и граничных условий для нулевого коэффициента особых трудностей не испытывает. В результате окончательная постановка задачи в главном приближении приобретает вид: n дР(0) mpβpµ ∂t k д2Р(0) _ 2kyдР^0 'pxдх2 d ∂y , t> 0, 0 дР(0) mβµ ∂t i. д2Ра0) kax дх2 2ky d дР(} ∂y , t>0, x>L, 0<у< (d/2), y=(d/2) dP (0) d^ P (0) d 2p (0) тв^ kx 1ky „ 1 =0, t> 0, 0 P(0)| = Pw, (-d/2) I x-0 dP(0 ∂x = 0, x-0 |y| > (d/2), P(0)| = Pa(0) P(0)= P(0)| , t> 0, 0 1ly-(d/2) Pa0)= P1(0)| t>0, X>L, 1 y-(d/2) . dP(0) . dP(0 , . , . kpx^— = kax^— , t>0, 0 dx dx x-L x-L p(0) 1 =0, Pa°1 =0, p(0) 1 =0. 11-0 lt-0 lt-0 Для упрощения аналитического решения дополнительно пренебрегаем вкладом потоков, ориентированных параллельно рассматриваемой трещине. Такие потоки ожидаемо малы, особенно при значительной протяженности трещины. Эту процедуру осуществляем формальным обнулением kx в уравнении (24) и исключением соответствующих условий из постановки задачи. 5. Построение главного приближения в пространстве изображений При построении аналитического решения начально-граничной задачи (22)–(29) со следом в уравнениях производной из внешней области наиболее эффективным является метод интегральных преобразований Лапласа– Карсона [20]. Переход в пространство изображений осуществляется путем умножения каждого уравнения и условия задачи (22)-(29) на множитель pexp(-pt) и последующего интегрирования по времени t в пределах от ∞ нуля до бесконечности [20], например, P(0)i (р) = Р j exp(-pt)P (0)(t)dt. В пространстве изображений математическая постановка задачи не содержит производных по времени и приобретает более простой вид: трвр^рР(0)i - kpx d 2P(0)i dx2 2kydP^ d ∂y y-(d/2) 0 твцрР(0)-kax d2Pa(0)i dx2 2ky d dp(}i ∂y , x>L, 0 тв^рР^)1 - ky d2P?* dy2 = 0, 0 P(0)i | = Pw , x-0 0 P(0)i= P(0)i 1 , 0 1 y-(d/2) P(0)i = p(0)i | , x>l, a 1 y-(d/2) P(0)ilx-L = ■ kpx ' = kax ■ , 0 x-L Решение уравнения (32) с граничными условиями (34) и (35) представляется как P^ = p(0)i exp 0 Pi0) = Pa(0)iexp mβµ d -1/ k P[y- 2 J у x>L, У>(d/2). Используя (37), (36) и (33), переписываем решение уравнения (30) в виде: p (0)i_ sh(Y(p)(L-x)) sh(Y(p)x) (0)i| 0 P = sh(Y(p)L) Pw +sh(Y(p)L) P L—L, ° , y>W2), где y(p) = mpβpµ kpx 2ky ImfJji p kpxd ky p. Аналогично преобразуем решение уравнения (31) с учетом (38) и первого условия из (36): P^ = p(0)i|^exp(-Ya(p)(x-L)), x>L, y> (d/2) Здесь Ya(p) = mβµ kax 2ky lmfJji p kaxd ky p. Второе условие из (36) имеет особое значение. Подстановка в него выражений (39) и (40) приводит к виду: (ch(Y(p)L) + Ya(p)kax sh(Y(p)L)} P(0)i| = Pw, \ Y (p) kpx J lx —L который удобен для рассмотрения двух следующих случаев, встречающихся на практике. Первый случай отвечает недеформируемой трещине. Такая модель применима к реальным условиям до достижения давлением критического значения Pc, провоцирующего дальнейший рост трещины, и соответствует эксплуатации добывающих и нагнетательных скважин при сравнительно небольших депрессиях (забойное давление в скважине ниже пластового) и репрессиях (забойное давление в скважине выше пластового). В этом случае выражение P(0)i| из (41) представляем в виде: p(0)i | _ = Pw/ fch(Y(p)L) + "-^pkx sh(Y(p)L)} , ' x — L / \ Y\p)kpx J что позволяет записать решение задачи определения поля давления в пласте с недеформируемой трещиной как P (0)i = Pw sh(Y(p)L) sh(Y(p)(L-x)) + (0) a= sh(Y(p)x) ch(Y(P)L)+ ^^pkxsh(Y(p)L); Y(p) kpx / Pwexp(-Ya(p) (x-L) ch(Y (P)L) +'^pYx sh(Y(p)L) Y\p)kpx p(0)i_ p(0)i ___Pw___p P1 =P =sh(Y(p)L)eXP x sh(Y(p)(L-x)) + (0)i P1 = \ , 0 , x>L, y>(d/2) sh(Y(p)x) ch(Y(P)L)+ Ya/Pkax sh(Y(p)L) Y (p) kpx / mβµ d / -v ply- 2) Xх \ ------ , 0 Pwexp(-Ya(p) (x-L)) ch(Y(P)L)+ Ya/Pkaxsh(Y (p)L) Y\P)kpx exp - mβµ d d k p[y- 2 J J, x>L, У>(d/2). Второй случай реализуется при достижении давлением в окрестности вершины трещины критического значения Pc , при котором наблюдается ее дальнейшее развитие. Такие условия имеют место при создании в = Pc, и условие (41) представляется в нагнетательных скважинах высоких репрессий. Для этого случая P(0)i | виде: x—L ch(Y (P)L) + kax (P^ntY^L = Pw, kpx Pc ( , Ya(P) _ I kpxmP 22 ky ymβ где(p) Y(p) V kaxтрвр у ^+d VkXmev Выражение (47) является неявным уравнением в пространстве изображений; его решение позволяет судить о зависимости от времени длины L трещины автогидроразрыва при критическом давлении Pc , что подчеркивает практическую важность уравнения (47). Решение задачи определения поля давления в пласте с растущей трещиной имеет вид: P (0)i = PW \T } fsh(Y (P)(L -x)) +PA sh(Y (P)x)) 0 sh(Y (p)L) Pw P^P = Paexp(-Ya(p)(x-L)), x>L, y> (d/2), P sh(Y(P)(L-XN' slHY (p)x) Pw 0 p(0)i = Pw 1 sh(Y (p)L) D (0)i m/p d x>L, y> (d/2). P1 ’ = PAexP -Ya (P)(X - L) -I k ///У - ^ J Можно показать, что при L → ∞ из полученных выражений следует известное решение для бесконечно протяженной трещины, которое совпадает с представленными в работах [17–19] и других. Таким образом, построено единственное нетривиальное решение задачи для нулевого коэффициента асимптотического разложения поля давления. Найденное решение составляет главную часть фильтрационного поля давления в нефтяном пласте, в котором создана трещина гидроразрыва, заполненная пропантом. Построение выражений для более высоких коэффициентов разложения осуществляется аналогично, а предложенная модификация асимптотического метода важна с общетеоретической точки зрения и может использоваться при рассмотрении широкого круга практических проблем. 6. Обсуждение результатов вычислительных экспериментов Итак, полученные выражения описывают поля давления в пласте с трещиной гидроразрыва в пространстве изображений Лапласа–Карсона, причем их аналитическое представление в пространстве оригиналов, которое могло бы применяться в практических целях, затруднено. По этой причине для расчетов пространственных и временных распределений поля давления в пласте с трещиной гидроразрыва прибегают к численным алгоритмам [21, 22]. Алгоритм Штефеста для обращения преобразования Лапласа [21] основан на стохастическом описании, предложенном Гавером Д.П. [22]. Алгоритм Ден Изегера [22] реализован с помощью гауссовских квадратур. В настоящей работе названные численные алгоритмы адаптированы для обращения преобразования Лапласа– Карсона, а результаты обращения с помощью обоих алгоритмов служат здесь для подтверждения достоверности расчетных данных, которые получены согласно выражениям (42)–(51). Алгоритмы численного обращения открывают широкие возможности применения в научной и инженерной практике отыскания физических полей и параметров процессов в технических системах на основе решений задач, построенных к настоящему времени в огромном количестве, но только в пространстве изображений. Использование указанных алгоритмов позволило создать программу-симулятор для расчетов полей давления в пластах с трещиной гидроразрыва, длина которой как постоянна, так и способна изменяться со временем при превышении критических давлений, при которых происходит разрыв пористой среды. Программа обеспечивает графическую визуализацию расчетных пространственно-временных распределений полей давления, скорости фильтрации и производительности трещин (меры способности трещины пропускать жидкость или газ через себя) в широком диапазоне параметров. При получении представленных данных вычислений участвовали параметры пласта: пористость m = 0.18, проницаемость ky = 1 мД, сжимаемость в = 10-10 1/Па, параметры трещины: полудлина L = 150 м, проницаемость kpx = 100 Д, полураскрытие d/2 = 2.5 мм, а также вязкость жидкости p = 10-3 Па^с. Величина перепада давления скважина–пласт составляла 50 атм. Рис. 3. Профиль давления вдоль трещины (у = 0 м) в разные моменты времени t, сут: 1 (кривая 1), 30 (2), 365 (3) На рисунке 3 приведены результаты расчетов давления в трещине гидроразрыва длиной 150 м и примыкающем коллекторе в зависимости от расстояния до скважины в разные моменты времени после начала закачки. Из анализа показанных кривых, следует, что перепад давления (разность между давлением флюида, вводимого в трещину, и давлением в пласте) в рассматриваемых по длине трещины точках и соответствующие градиенты давления малы в сравнении с градиентами в прилегающем коллекторе. Такое распределение давления благоприятствует развитию трещины при закачке воды в пласт. Рисунок 4 демонстрирует результаты расчетов поля давления после начала закачки в примыкающем коллекторе в поперечном у, км Рис. 4. Распределение давления в коллекторе вдоль оси y при различных расстояниях x от скважины, м: 10 (а), и 151 (б), в разные моменты времени после начала закачки t, сут: 1 (кривая 1), 5 (2), 10 (3) к трещине гидроразрыва направлении на различных расстояниях от поверхности скважины, то есть в трещине и вне ее. Анализ приведенных кривых показывает, что размеры зоны влияния закачки, ориентированной поперек по отношению к трещине, больше ее длины. Сравнение кривых рисунков 3 и 4 позволяет констатировать: размеры зон возмущения по пути эволюции трещины и перпендикулярных ему значительно отличаются. На рисунке 5 представлена зависимость от времени давления в вершине трещины. Приведенная кривая свидетельствует об относительно быстром установлении давления (порядка суток). При этом достигаемая величина давления близка к амплитудному значению. Заметим, что в отсутствие трещины давление на таких расстояниях не имеет столь высоких значений в течение всего времени эксплуатации скважины. Значительное различие давлений в отсутствие трещины на расстояниях порядка ее длины объясняется тем, что наряду с повышенным диссипативным перепадом существенное влияние оказывает гидродинамический напор, связанный с пространственным ускорением потока при Рис. 5. Динамика давления во времени в вершинерадиальном течении в призабойной зоне скважин. трещины: y = 0 м, x = 150 м Кривая на вложенной иллюстрации приведена для оценки времени задержки — временного интервала, по истечению которого давление начинает заметно увеличиваться. Он составляет порядка 10 с. В отсутствие трещины, как показывают вычислительные эксперименты, времена задержки на несколько порядков выше. Отметим, что при использовании программы-симулятора графики такого рода позволяют оперативно, образно говоря, «с помощью курсора на дисплее компьютера», определять время достижения давлением критического значения, при котором начинается процесс неконтролируемого развития трещины (автогидроразрыв). 7. Заключение Итак, на основе асимптотического метода в пространстве изображений Лапласа–Карсона найдено решение задачи определения поля давления в пласте с трещиной гидроразрыва конечной протяженности. На основе алгоритма численного обращения осуществлены расчеты пространственно-временных распределений давления в трещине и окружающем коллекторе. Установлено, что давление в трещине сравнительно быстро становится близким к давлению нагнетания, а основные изменения давления по пути развития трещины сконцентрированы в области, размеры которой существенно меньше размеров зоны возмущений, ориентированной поперек трещины. Показано, что значения градиентов давления в коллекторе в направлении роста трещины намного больше величин градиентов в боковых от трещины зонах коллектора. Это создает благоприятные условия для эволюции трещины. Примененная модель определения полей давления позволяет оценить время достижения в вершине трещины критического давления, при котором начинается процесс автогидроразрыва в области влияния нагнетательной скважины. Описанный аналитико-численный подход и найденные решения открывают новые возможности для исследования полей давления в нефтегазовых пластах с трещинами гидроразрыва.