Полиномиальные решения дифференциальных уравнений в частных производных с постоянными коэффициентами I
Бесплатный доступ
Исследуется существование полиномиальных решений систем линейных дифференциальных уравнений в частных производных с постоянными коэффициентами общего вида.
Полиномиальные решения, гармонические полиномы, линейные уравнения в частных производных
Короткий адрес: https://sciup.org/147158665
IDR: 147158665 | УДК: 517.956
Текст научной статьи Полиномиальные решения дифференциальных уравнений в частных производных с постоянными коэффициентами I
-
1. Введение
-
2. Пространство полиномиальных решений
Предлагаемая вашему вниманию статья посвящена построению и исследованию полиномиальных решений систем линейных дифференциальных уравнений в частных производных с постоянными коэффициентами общего вида. Изучению полиномиальных решений конкретных уравнений в частных производных посвящено много работ. В основном это исследования поли-гармонических [1, 2], поливолновых [3], тепловых [4] и других полиномов [5]. В [6] исследуются базисные системы полиномиальных решений множества различных уравнений, однако при построении решений существенно используется структура дифференциального оператора уравнения. Следует отметить, что работа [7] посвящена такой же проблеме, но только для системы специального вида (несколько уравнений и только одна неизвестная функция). В работе [8] строятся полиномиальные решения полигармонического уравнения с помощью формулы Альманси, в [9] исследуется зависимость полиномиальных решений от коэффициента при старшей производной, а в [10] сделаны первые попытки общего подхода нахождения полиномиальных решений. Существование полиномиальных решений краевых задач для уравнений эллиптического типа исследовал С.М. Никольский [11]. В [15] построены полиномиальные решения неоднородного полигармонического уравнения и уравнения Гельмгольца. В настоящей работе не имеет значения ни структура оператора уравнения, ни тип дифференциального уравнения. В разделе 2 исследуется размерность пространства полиномиальных решений систем дифференциальных уравнений и в теореме 4 предложен метод, сводящий отыскание решений системы уравнений к решению только одного уравнения, но более высокого порядка. В качестве примера применения полученных результатов доказана разрешимость в гармонических полиномах общего уравнения вида B{D)u{x) = и0(х), где и0(х) - гармонический полином.
Рассмотрим линейный дифференциальный оператор порядка q с постоянными коэффициентами вида q цо>^LAD^ LAD>>= 2 A«D“^ (0
j=k \a\=j где L^D)^ 0, aeNg (здесь N0sNu{0}), Da = D“'•■ • D“n и матрицы Aa принадлежат
L(C5,C') - пространству линейных отображений С5 в Cz (s,f е N). Определим множества: к
?к - № = 2 Раха : Ра е С}, И^ - {Г W = 2 pj ^ : W G РЛ 1«1=к /=0
и обозначим Р' = lim Uj[. Очевидно, что все эти множества могут быть наделены естественной £->СО структурой линейного пространства над С .
Карачи к В. В. Полиномиальные решения дифференциальных уравнений________________________8 частных производных с постоянными коэффициентами I
Рассмотрим систему линейных дифференциальных уравнений с постоянными коэффициентами вида
ЬфМх) = /ф, (2)
где будем считать, что /еР(, и е Р5 и х е R". Множество функций - классических решений системы (2) (и ё О'7 (R” ) ) при / = 0 обозначим kerZ(D). Основным средством исследования этого параграфа является следующая полуторалинейная форма на линейном пространстве Р5:
где (.,.) - скалярное произведение в С5. Аналогичная форма была рассмотрена в [12], но на пространстве Рк.
Покажем, что форма (.,.) является скалярным произведением в Р5. Нетрудно проверить справедливость формулы
(3) О, иначе где обозначено х“ = xv ■ • -х“" (ln,! = tn!n\), а порядок на Nq определяется так: a< р <^>^1^1п, at < Pj, где In = {1,2,...,«}. Далее, в соответствии с (3) будем иметь
(p4x),Q4x)} = ^ оДРафЛ а
Полученное равенство позволяет нам утверждать, что форма (.,.) удовлетворяет всем аксиомам скалярного произведения в Р5. Форма (.,.) полуторалинейная
^ЛРЧх) + МНЧхШЦ = ^^Ра + PR^Qa) = а аа
(Пт),1№)) - X £ ^Qa,Pa) = ^РЧхШЦ аа и положительная
^рчх\рчх^=х<раФф=X«!hll2 > °, аа если Ps (х) * 0 .
Введем оператор Tm(L): U^ м U^,, который определяется по оператору ЦП) и при т>к имеет вид min(m,) TmW= £ Ц^, i-k где T^ : 1ф t-> U^ - проектор
т(/)£№)=£ем i=0 /=0
причем Q‘ (x) g Р/ , L^x) ^^^x" и как обычно А* = Qj(). а
Лемма 1. Для любого оператора вида (1) имеет место равенство
Z(n)U^=U^©ker4(Z).
Доказательство. Нетрудно убедиться, что для P4x)eUsm справедливы равенства q т min(m,qr)
Рф)РЧх)^2к^)Р}Чх)= Z 11к(О)РРДх),(4)
i=k j=i i=k/=0
Математика а следовательно, Z(£>)U^ сU^ . Теперь покажем, что для РДхЭеИ^ и Q? фе\Ут_к имеет место равенство
(Т(О)Р^ (х), 0 Ц = (ps (х), Тт ф)^ (х)). (5)
Действительно, из равенства (4), заменяя i ->т-1, а затем, меняя порядок суммирования и обозначая при этом а = max(m - q, 0), b=m-k, получаем min(m,9) m-i b у
^)РДх) = ^ ^LAD)P^x) = ^Lm^D)P^^^ i=k j=0 i=aJ=0
» » ь y=0 i=max(y,a)
Используя очевидное утверждение
Р$Ф е Фр,д5ф е U^ => (p4x),Q4x)\ = ^^Pf ф, $(7)
i=0
находим
^UD)P4x),Q\x)) = X ^‘фф‘ф) = X £ \Lm-j 1=0 /=0 y=max(i,a)
Теперь покажем, что имеет место равенство
(4 ф^ (х), Q*, ф} = ^ (х), ХкФОг to) • (8)
В самом деле, так как РД^ОР^/С*) с Р/, то
= ^ФО^^Ц = {PkAx\L кФЙ ф) •
Используя полученное равенство, находим b ь уф^ф^фу^ £ ^-Мьт-АШх^ 1=0 j=inax(i,a)
и значит, возвращаясь по цепочке (6) назад, получаем min(m,g) т- j ^Ьф^фф‘фу £ ^^Ф'ТЧх^фУ j=k i=0
min(m,i7) и min(m,^) т+к
= S Тдр^фФенАУ 2 Ц^ф,1Дх)2‘нф). j=k i=j j=k i=j
Теперь следует заметить, что в соответствии с определением оператора Ттф т1п(т,у)
Ттф0ф= Е ь,фТи_к^ф = j=k т1п(т,у) m-j+k min(m,) т+к
= X Z р,Ф2‘ф= £ У,Т)Ф0НФ-j=k i=0 j=k i=j
Поэтому, если воспользуемся (7), то будем иметь min(m,<7) т+к
^ф^ь^фу ^У^хУьЧх^^фУУффЧхШфУ j=k i=j что совпадает с (5).
Если теперь предположить, что ЗР‘феХ]‘т_к и Р* ф V Ьф^ХЗ^, а затем обозначить
Hs ф = Тт фР1 ф, то согласно (5) получим
У5 ф, н$ ф^ = уф)ф ф, р‘ (х)} = о,
Карачик В.В. Полиномиальные решения дифференциальных уравнений_______________________________в частных производных с постоянными коэффициентами / откуда сразу следует, что Tm(L)P‘(x) = 0, а, значит, верно включение
Uzm_,0Z(Z))U^CkerZm(Z).
Если в (5) выбрать Q‘(х) е ker Tm(L), то VP\x\^L(P)Ps(x),Q4x)^ = 0 и мы получаем обратное включение ker Tm(L) с k5‘m_k О Z(Z))U^ . Лемма доказана. □
Следствие 1. Из леммы 1, при Дх)е VS‘m_k, следует простое необходимое условие существования решения уравнения (2), принадлежащего U* . Оно имеет вид
I(xV(x) = '£Pi(x')^3i
Доказательство.
В самом деле, пусть условие следствия не выполнено, т.е. пусть ЦтШ^)-^.
Rj(x)
и
^i
TmW(x) = X Uxf^J^ £ У (9)
i=k j=0 i=k /+j Будем говорить, что квадратная матрица ЛДх), элементы которой т,у(х) принадлежат Р = Р1, невырожденная, если полином detZZ(x), как элемент Р отличен от нуля, т.е. det3Z(x) * О в Р. Теорема 1. Если матрица Z(x) - квадратная, а матрица ЬДх) - невырожденная, то для оператора Z(Z)) вида (1) верно равенство Z(Z))Uf„ = \}lm_k (,s = t). Доказательство. Покажем, что в условиях теоремы ker Тт (Z) = {0}, а значит, в силу леммы 1 U^ О Z(Z>)U„ = {0} и теорема будет верна. Пусть Pz (x)g ker Tm(Z). Напомним, что U'OT_fc -область определения оператора Tm(Z). Сначала докажем справедливость утверждения т-к Р^хД^РКх^Р^хД». i=j Действительно, из равенства (9) для оператора Tm(L) следует, что однородный полином наименьшей степени, входящий в Тт (L)Pe (х), будет иметь вид £ k{x)Pj (х) • Следовательно, из верности утверждений det Lk (х) = 0 <=> det £ к(х) = 0, detz.(x) * 0 => ^£к(х)Р*(х) = 0^РЧхД О), (10) которые становятся очевидными, если их рассмотреть над полем частных О = y\x)/Q(x): Р(х), Q(x) е Р} кольца Р, сразу найдем Pj (х) = 0 . Применяя доказанное утверждение т-к раз к произвольному полиному из kerTm(Z), приходим к выводу, что он должен быть нулем. Теорема доказана. С Лемма 2. Имеет место следующее разложение пространства U^.' U^=(kerZ(Z))nU^®Tm(Z)U^. Доказательство. Рассмотрим подпространство и^ = ТД1?)\31т_к пространства U^ и найдем элементы из U^,, которые ортогональны ему. Имеем Математика _________________________________________ (вЧхУ^^ = 0 => ^Чх^Цу^ 0 kerTm(Z)^ = О, и следовательно, в силу леммы 1 и (5) запишем ^L(D)RS (%),Z(D)U^ = 0. Полученное равенство справедливо лишь при Ps(x)ekerZ(D)nU^. Поскольку приведенная выше цепочка утверждений обратима, т.е. R4x) е ker Z(Z)) nU^ =>(К4х)д№>) - О, то лемма доказана. □ Следует отметить, что в силу (5) оператор Tm(L) является сопряженным к оператору ЦОД действующему из U„ в U^, а именно С (О) = Tm(L). Определение!. Систему полиномов Pi(x\...,Pk(x') с коэффициентами из некоторого линейного пространства над С, удовлетворяющую условию Vi = l,k, deg7)(x) = m, назовем линейно независимой по старшему члену, если для любых аъ...,ак из С выполнено равенство deg(a]P1 (х) + • • • + акРк (х)) = т. Из данного определения следует, что если полиномы Д (х),...,РДх) однородные степени т , то линейная независимость по старшему члену совпадает с линейной независимостью. Теорема 2. Максимальное число линейно независимых по старшему члену полиномиальных степени т решений однородного уравнения (2) - Nm(n,k) находится по формуле / т + н-1 ) N^n^-sX -Z I и -1 J ^m-k-vn-XA , , + dimPm-dirnPm_1, И — 1 J (И) в которой обозначено i>m Доказательство. Установим, что т dim (12) ' /=о Для этого докажем следующее утверждение. Если {Р^ (х): a g Л} - базис в пространстве ker HD) о U^_], а {Pj (х): Д е 5,degP^(x) = ти} - максимальная система линейно независимых по старшему члену полиномиальных степени т решений однородного уравнения (2) (к этой системе нельзя добавить полинома степени т из ker£(Z))nU^, чтобы она осталась линейно независимой), то система полиномов ^Рд^х\Рр^ху.аеА,РеВ^ является базисом в пространстве kerZ(D)oU^. Действительно, если некоторый полином Q4x)e kerZ(Z))nU^ нельзя представить как линейную комбинацию полиномов этой системы, то система ^Qs (х), Рр (х): Р^В} линейно независима по старшему члену, поскольку в противном случае Эс е С,Эс^ е С, cQ4x^ СрР= (х) е kerЦП^гл U^„ Дей а это означает, что Зса е С, сОНх^^СрР^Х^^сЛ^У (ЗеВ а^А что противоречит допущению о непредставимости полинома Q4x). Однако линейно независимость по старшему члену системы ^Qs(x),Pp(x): р£ В} тоже невозможна в силу максимальности Карачик В.В. Полиномиальные решения дифференциальных уравнений _______________________________в частных производных с постоянными коэффициентами / системы {Z^ ф: ^еВУ Итак, система полиномов ф® (х), Р^ (х): а е А,/3 g В} - базис в пространстве ker L(D) nU’r Поэтому dim f ker L{D) nU^ = Nm (n, k) + dim ^ker L{D} n U^_] ^j. Отсюда по индукции устанавливается справедливость (12). Из общих свойств линейного оператора T^L) находим dim(zm(Z)Uzw_A) = dimUzm_ft - dim kerTm(L\ а поэтому из леммы 2 с учетом (12) следует, что ^ Nt (n,k) = dim U^ - dim U^.^ + dim ker Tm (L). ;=0 Выписывая аналогичное равенство при т = т -1, а затем, вычитая получившееся равенство из имеющегося, будем иметь Wm(n,£) = dim U^, -dimU^ -dimU^ +dimU^_, + + dim ker Tm (L)- dim ker Tm_x (L). Нетрудно заметить, что т + п -1 п-1 dimll^ -dimU^_] =dimP^ =sdimP^ =5 а значит найдем fm+и-Л fm-к+п-У N (n,к) = s\ -Z + dim ker7m(Z)-dim kerZm_](Z). (13) n —1 J и —1 ) Как отмечалось в следствии 1, если в выражении ЬфР*(х) отбросить все члены, порядок которых выше т, то получим Tm(L)Pl(xy Поэтому, если обозначить ^S=Ui>m^’ то для Р1 (х) е U^ будем иметь ШРЧх^-ТтЩР\х^^5. Если Р'(х) ekerZm(Z), то L(x)P\x)g W5 и значит Р'(х)&У^. Верно и обратное. Если P\x)gV^,to L(x)P‘(x) е W5 и значит Tm(L)P! (х)g Ws , а это означает, что Tm(L)Pl(x) = 0, т.е. ^(х) g kerTm(L). Значит, kerZm(Z) = V^ и из равенства (13) следует утверждение теоремы. Доказательство завершено. □ Пример!. Пусть 8к(х,у) и Rk(x,y) - некоторые полиномы, не имеющие общих делителей в кольце С[х,у] полиномов над С. Рассмотрим два дифференциальных уравнения: 8кфх,ОуМх,у) = 0, Rk^Dx,DyW^ = 0. Существуют ли полиномиальные решения этих уравнений, общие для обоих из них и как много таких решений [7]? Определение 2. Полиномиальное решение дифференциального уравнения с однородным степени к оператором Z^Z^Z^) будем называть простым решением, если степени каждого монома, входящего в это решение, либо по х, либо по у меньше к . Запишем рассматриваемые уравнения в виде системы (8кфхф?У ЦВхФуМх,у)= к(х,у) = 0. (14) фкФхФу) ) Найдем Nm - число линейно независимых однородных полиномов степени т , которые являются решениями обоих рассматриваемых уравнений. Для этого воспользуемся теоремой 2 для системы (14) полагая s = l, t=n=l, q = k и значит в этом случае L ф у) = С (х, у) = (Sk( х, у), Rk (х, у)). Математика Найдем число Хт = dim К^ = ^^(х) е U2_t: Z(x)J*2(x) е (Jj>m Р('| • Используя равенства ^к (х, у) + Rk(x,y))\ = Sk (х, у)Рт_к (х, у) + Rk (х, y)Qm_k (х, у) = О \Vm-kVx,y)) и учитывая, что полиномы 8к(х,у) и Qk(x,y) не имеют общих делителей, можем утверждать, что полином Рт_к(х,у) должен делиться на полином Rk(x,y) и выполнено равенство Qm-k (х> У)= ~^к (%> У^Рщ-к (х> У^Рк ^Х’ У) ■ Поэтому т - к > к и поскольку полином Pm_k^x,y^!Rk^x,y^ имеет степень т-2к и может быть выбран произвольно, то таких однород-ных полиномов от двух переменных будет , а значит ( т-2к + Х Ли — = , Следовательно, из равенства (11) получаем ( ту1) , Г2 т-к +В (т-2к + 1 + откуда Nm = 0 для т > 2к, Nm = 2к-т-\ для 2к > т > к и Nm = т +1 для к > т > 0. Таким образом, все полиномиальные решения, общие для рассматриваемых уравнений - простые. Предложение 1. Если матрица £(х) символа оператора системы (2) квадратная, а матрица Lk (х) символа оператора младших производных этой системы невырожденная, то решение системы (2) существует при любой правой части /(х) е\Ут_к и максимальное число линейно независимых по старшему члену полиномиальных степени т решений однородной системы (2) имеет вид ^щ + и-1) (m-k-vn-V Nm(n,k) = s\ -5 л-1 ) ( л-1 J Существование решения системы (2) сразу следует из теоремы 1. Значение N^n,^ получается из теоремы 2, если учесть, что в данном случае Lk(x) У 0 => Lk(x) у О и значит полином низшей степени, входящий в Е(х)Р‘(х), будет иметь вид Lk(x)P{(х), где Р, (х) - однородный полином низшей степени, входящий в Р((х) и 1<т-к. Поэтому включение Z(x)Pz(x)e[J(mP,s (5 = /) возможно лишь при Р1 (х) = 0, а значит V^ = {0}. Замечание 1. Если квадратная матрица Lk(x) невырожденная, то используя предложение 1 и п+1 п+т п+т+1 и известное комбинаторное тождество + ++ = находим I П I П I n + l J ™ т<г + п_2Л ^^(Л-1Л) = 5^ /=о z=o\ п 2 ) I-к + п-2\ (т + п-1\ (т-к + п-\ = 5 -5 = N>,kY л-2 ) (^ л-1 ) ( л-1 Например, максимальное число линейно независимых однородных степени т гармонических полиномов от л переменных равно максимальному числу линейно независимых гармонических полиномов до степени т включительно от л -1 переменной. Пример 2. Подсчитаем число линейно независимых по старшему члену полиномиальных степени т решений системы уравнений вида: М» "«Ху - V^ = 0, U^-Uyy-V^ 0, возникающей при исследовании некоторых задач термоупругости. Перепишем систему в виде D^-D1^ Ь1 -D2 ^ХХ УУ Карачик В.В. Полиномиальные решения дифференциальных уравнений_______________________________в частных производных с постоянными коэффициентами / Для этой системы имеем Г = s = 2, и = 2, £ = 1, q = 2 и кроме этого det Lx (х, у) = det Ц (х, у) = 0, но det Цх, у) Ф 0. По аналогии с примером 1 обозначим Лт = dim V^. Нетрудно видеть, что Л 2 2 (лй)^^ х х у I Lu^ pt = 0=0 для 0т_гфу),Рт_х = хР^г,Qm_x = -yRm_2. В силу произвольности йт_2(х,у) будем иметь Лт = т~1 |. Поэтому и значит Nm = 3 для т > 2 и Nm = 2 для т = 0,1. Теорема 3. Для любого оператора ЦО) вида (1) верно равенство ЦО)Р5 =Р' 0kerZ(x). Доказательство. Положим Р5ф е Р5, ()‘ф е Р'. Если обозначить k +I = т, то из равенства (8) нетрудно получить ^кф)рцхшЦ=^мМ^Ц- Здесь уже можно считать, что числа к,1 и т независимы, поскольку при тФк + l мы имеем очевидное тождество 0 = 0. Поскольку Ps(x) = ^m7^(x) и 0z(x) = ^/0/z(x), то, суммируя это равенство по I и т и полагая к = 1, получаем ^Д ф)Р$ ф, Q‘ ф} = (р5ф, Цф^ ф). Если полученное равенство просуммировать по / от к до q, то найдем ^ЦО)Р8фф‘ф^ = ^фДф^ф^. Отсюда сразу следует, что для оператора ЦО): Р5 н> Pz справедливо равенство Дф) = Цх): Pz м Р5. Проводя рассуждения, аналогичные сделанным в конце доказательства леммы 1, приходим к равенству ЦО)Р$ = Pz О kerZ(x), завершающему доказательство теоремы. Имеет место утверждение аналогичное предложению 1. Предложение 2. Пусть матрица Еф символа оператора системы (2) квадратная. Тогда если det Цх) Ф 0, то полиномиальные решения иф е Р5 системы (2) существуют для любой правой части /фсPzЦ-t). Это утверждение следует из того очевидного факта, что если deti(x)^0, то однородная система ЕфР'ф = 0 имеет только нулевое решение Р1ф = 0, т.е. kerZ(x) = {0}. Тогда из теоремы 3 следует, что ЦО)Р5 = Pz. Пример 3. Рассмотрим известную систему уравнений Ляме 50 . — Aи, + Ц"•"” - /ф) i = ^n, ОХ, где <Эи - объемное расширение, имеющее вид 0М = div и . Запишем эту систему в виде [13] Еци = Ам + р,Ои = / (х), (15) где О = й\аЦОХх,...фХп)Кй\а%фч,...ф:(п), а матрица А состоит из одних единиц, т.е. А = (1). . Обозначим через Е единичную матрицу. Убедимся, что для любого ц е С, но цф-\ верно равенство Ефп =Р". Для этого воспользуемся предложением 2 и покажем, что Математика det Е (х) * 0 . Подсчитаем det Еи (х). Продифференцируем det Ец (х) по параметру р. Это воз можно в силу полиномиальной зависимости det£p(x) от р. Воспользуемся правилом диффе ренцирования определителей. При дифференцировании первого столбца определителя detEM(x) будем иметь Э//(х1,х2,...,х,7) = х2 det рх2 ... рх„ ^+|х|2 ... рх2хп 2 , 12 'И ВЧхп ... рхп + \х\ Если продифференцировать к -й столбец определителя det Е^ (х), а затем переставить в нем 1-ю и к -ю строки, а затем 1 -й и к -й столбцы, то получим АДхк,х2,...,хк_х,хх,хк^х,...,хпУ Таким образом, можно записать (detE^x)) =ЛДХ],х2,...,х^ + ЛДх2,:1ч,...,х^ + --- + ХДх,,,х2,„^ (16) Исследуем зависимость полинома А^ (х) от р. Если продифференцировать этот полином по р, то нетрудно заметить, что его производная будет равна нулю: при дифференцировании первого столбца мы получим нулевой столбец, а при дифференцировании / -го столбца (2 < z < и) мы получим первый столбец, умноженный на xz. Значит полином АДх) не зависит от р. Поэтому Аи(х) = X2 det 1 вч Ч А^+И2 • рхп рх2хп = 4)(х) = х2 х„ рхгхп . 2 < .2 .. //Xn + |x| Подставив найденное значение Ац (х) в (16), находим Это означает, что det£A(x) = //|x|2"+5(х), (17) где В^ - некоторый полином. Для того, чтобы его найти достаточно положить р-0 в (17). Будем иметь | х |2'7 = det Ео (х) = В(х). Таким образом, detE^x) = (1 + р) | х I2" , а значит det E/Z(x)^ О при рф-\. Хорошая операторная матрица А-Е возмущается хотя и не малой, но очень плохой матрицей pD, для которой rankZ)(x) = l и поэтому она мало влияет на действие оператора А • Е: число однородных степени т полиномиальных решений однородной системы (15) при всех рф-\ одинаково и совпадает с числом однородных гармонических полиномов степени т умноженным на число переменных и. Где искать решения однородной системы (2) устанавливает следующее утверждение. Предложение 2. Имеет место равенство Ps = (ker L{D} n Ps) Ф Е(х)Р'. Доказательство проводится аналогично доказательству леммы 2 с той лишь разницей, что вместо леммы 1 надо использовать теорему 3. Определение 3. Будем говорить, что вектора £ц)(х) из Р' (i е /т) полиномиально незави симы, если 2 ^(х)40(х) = 0 => Vz 6 Im, Д (х) = О, 1=0 где /)(х)еР. Рангом матрицы Цх) назовем максимальное число ее полиномиально независимых столбцов. Карачи» В.В. Полиномиальные решения дифференциальных уравнений_______________________________в частных производных с постоянными коэффициентами I Предположим, что матрица Цх) обладает следующим свойством: если ранг матрицы Цх) равен г , то г ее первых строк и столбцов полиномиально независимы. В противном случае мы можем переставить уравнения системы (2) и перенумеровать ее неизвестные так, чтобы это свойство было выполнено. Лемма 3. Существует замена переменных и = Аф)$ с невырожденной матрицей А(х), приводящая систему (2) к виду "dia^Rm(D),...,R(r\D)) о" 8(x) = f(x). v Тф) О, Доказательство. Рассмотрим матрицу Еф как оператор, действующий из О5 в О1, где 0s = < ^ Са8аф: Са е Cs,Sa(x) е СП и О - поле частных кольца Р^Р1 из теоремы 1. Тогда понятие полиномиальной независимости из определения 3 становится эквивалентным обычной линейной независимости в О5. Пусть ранг матрицы Еф равен г . Выберем в пространстве ЕфО5 следующий базис: е,(х) = (о,...,О,/?(/)(х)Д^^ где ielr, R^x) и Т дф (j = r + l,...,Z) - полиномы по х, выбранные таким образом, чтобы существовало полиномиальное решение w(x) = A^(x) системы уравнений Z(x)w(x) = еДх). Такие е,ф и решения А8ф существуют, поскольку можно решить первые г уравнений системы Е(х)н(х) = е,(х) с ^'\х) = 1 в 0s, затем выписать полный вектор Z(x)Af(x) и положить значение Т^ф при y = r + l,,..,z в векторе в(ф равным j-й координате вектора Z(x)A^(x). Тогда Л*(х) будет решением системы Ефиф = е,(х) с построенным е,(х). Если теперь домножить эти е,- ф и Л ■ (х) на общий знаменатель всех дробей, входящих в них, то получим е, (х) е Pz, Л;(х)еР5. Определим Af (х) для значений z = г + l,...,s, требуя, чтобы они были линейно независимыми полиномиальными решениями в 0s системы Z(x)w(x) = 0. Это тоже можно сделать, поскольку ранг матрицы Z(x) равен г . Теперь составим матрицу Л(х) = ^Af(x),...,A^(x)). Она неособенная, поскольку все вектора Af (х) по построению линейно независимы в О8. Матрица Л(х) обладает свойством Обозначим через 3, j символ Кронеккера. Теорема 4. Пусть матрица Z(x) - квадратная, невырожденная, тогда всякое полиномиальное решение системы (2) может быть записано в виде Математика u(x) = ^3w(D)Pu4x\ (18) 1=1 где 9^'Чх) - полиномы из Рх, удовлетворяющие уравнению Цх)ЗиЧх) = КиЧх)е(, в котором е, =(5Xi,...,3sj)T, R^\D)P^'\x) = /Дх) и R^(x), Р^Чх^еР. Доказательство. Нетрудно непосредственно проверить, что полином м(х), определяемый по формуле (18), действительно удовлетворяет системе (2) W) = X Ьф^Чп^Чх) = f еДиЧО)РиЧх^ = £ ej^ - № Z—1 J-l Z = 1 Покажем, что любое полиномиальное решение системы (2) может быть записано в виде (18). Пусть м(х) g Р5 - решение системы (2). По условию теоремы ранг матрицы Z(x) равен 5 . Воспользовавшись леммой 3, с помощью замены переменных и = A(D)w систему (2) в случае s = t запишем в виде diag(^^.D),...,/?(^D)^^ Так как detA(x)^0, то на основании предложения 2 по полиному w(x) всегда можно найти полином w(x) е Р' такой, что u(x) = A(£>)w(x). Вводя обозначения и(х) = A(Z))w(x) = <9(n(Z))w1(x) + 3b4DHW = £ 9V4D)PU4x\ i=i Теорема доказана. □ Рассмотрим другой пример использования полученных результатов. Пример 4. Пусть дифференциальный оператор с постоянными коэффициентами Вф) = X baD\ k<\a\ Задача!. Найти полиномы и0(х)еГ такие, что существует решение уравнения B(D)w(x) = w0(x), принадлежащее множеству У. Для решения задачи 1 воспользуемся предложением 2. Верно следующее утверждение. Теорема 5. Задача 1 имеет решение при любом полиноме ы0(х) g У. Доказательство. В соответствии с леммой 2 и формулой Альманси (см. например [16]), полином S(x) можно единственным образом представить в виде В(х) = Я(х) + ||х||25(х), где Н(х) - некоторый гармонический полином, причем в силу условия задачи И(х) Ф 0 и Н(х) = Н(х). Разделим множество У на два множества У^ и У^ - четных и нечетных гармонических полиномов по некоторой переменной х-. Обозначим через Н^°Чх) и Н^Чх) четную и нечетную по х- компоненты полинома Я(х) = Н^Чх)* Н^ЧХ). Используя результаты [10] нетрудно доказать, что для каждого Н^ е У имеют место равенства со HW(x) = £ (-D^?+Z'^Чх\ i - 0,1, 5=0 Карачик В.В. Полиномиальные решения дифференциальных уравнений _______________________________в частных производных с постоянными коэффициентами / где х = (хх,...,х^_А,х}_х,...,х„) и ^^(л):5еNoj — некоторая система полиномов, обладающая свойством нормируемости [17], Ь^Х^Н^х), (19) где обозначено A^.^A-Z)2. Ясно, что Н^Хх) = Xj)HqXx) и Hq°Xx) = H(x)\x 0, Н^Хх) = Н'хХхХ=0 . Поэтому полином Hw(x) определяется однозначно с помощью Н(х)^х.=0 , а Н^ф с помощью Н'хХх\х,=о • Значит Vw = f^ (-1)5x^Xf^ i = 0,1, 5=0 где р(0 при / = 0,1 два экземпляра пространства полиномов от переменной х. Вычислим множества Н^ф)У^ . Имеют место равенства Н<°Хп)У<п = ^ (-1)' П^’Н^ф)^ Н/х^А^^0 = 7=0 7 5=0 ,2s 2/+jJ Q5 qq '^У’М/1 - z ln^‘% X VZU- 7=0 5=0 co ( oo д' ^h<«4iV'-I ИГхГН) £ ^«."W" v2Zl- 5=0 (/=0 Xя)- , Проводя аналогичные вычисления для Н^ф)У^ будем иметь 00 00 00 со Н^фУ^^Х^^ У х 7=0 7 5=0 7=0 5=7+1 2s—27—1,! од да Л^^ х(-1Г' ^---н^фХпР^ =У У (-l)s+1^+1Чэ х (2/ + 1)! 1 0)Г J 7 (2/ + 1)! 5=0 7=0 ЛЦ) (2/ + 1)! н^ф)р№ сФ. или в общем виде <х> ( оо д7+1—/ 5=0 (/=0 (2/ + 1)! Сходимость рядов, входящих в полученные соотношения, очевидна, поскольку эти ряды представляют собой конечные суммы. Используя эти равенства, нетрудно найти Нф)У = (H^XD) + H^XDW^ + ^G)) = (Н№(В)У№ + НтфХХХ + 4HkXXDy№ + H№XDyVh = f (-1Г х2Х 'Xn f У У ylr^'Hi^^vA + s-0 (/-0 7-0 Uz + O! ) oo ( 1 oo д/+1—z s=0 (/=0 /=0 + 1 <Л J Ясно, что H{D)V aV поскольку М1ф)У -Нф^У = {0}. Поэтому оператор Нф) дейст вует из У в себя Нф}: V -> У . Из (19) следует, что У изоморфно р2 . Поэтому оператор Нф) порождает следующий матричный оператор: Математика Аф): <Р0), JG)J Афф 00 д/ У^Лн^ф) со _у_^Л_Н^ф) ( Й(2/ + 1)! 1 Найдем образ оператора Аф). Для этого, в соответствии выписать полином det А(х) . Имеем у_^Ш_н«ф) (2/ + 1)! ' со д/ с предложением 2, необходимо V det Аф = ^||x||2/’!^(0)(x) + V/=o ) м=о Предположим, что det^(x) = O в Р. Поэтому коэффициенты полинома det^(x) равны нулю, а значит, равны нулю и коэффициенты полинома det Аф при х е С" 1. Будем считать, что х е С” . Вспоминая определение полиномов, Н^\х) записываем н^ф^ф^-’н^ф, / = 0,1 /=о и поэтому из (20) легко найдем deU(x) = (я(0)(х))2 -^Нтф^ где z2 = -1 и значит йе1АфЦн№ф + Нтф^Н№ф-Нтф"\ „ . Таким образом, вспоминая, что Нф = Н^ф + Н^ф, будем иметь det Аф = Нф,...,i||х||,...,хп)Нф ||х||,...,хп). Нетрудно видеть, что аргументы у полиномов Нф справа удовлетворяют условию ||х||2 = х2 + ■ • • + х2 = 0, хеСп. Рассмотрим полином Тф = НфНф, где Нф = Нф,...,-Хр...,хп). В силу сделанного предположения det^(x) = O будем иметь ||х||2 =0=>xv = ±z||x|| => Тф = 0 . Теперь, применяя теорему Гильберта о нулях полиномов [14], получаем (Ml" = 0 =>Тф = O^apeN, а^ф, Трф = 6(х)|]х||2. Из факториальности кольца многочленов над С и неприводимости над R многочлена ||х||2 (и > 2) будем иметь (зем ^x)^||2o/x)jU(3CW Я(х)=н2д2(х)), что противоречит согласно предложению 3 при Тф) = А включению Нф, Нф g V . Это означает, что наше предположение detH(x) = O неверно. Воспользовавшись предложением 2, найдем Аф)р2 = р2. Отсюда, вспоминая определение оператора Аф), сразу получаем Нф)У = V и значит Вф)У = V. Теорема доказана.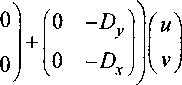
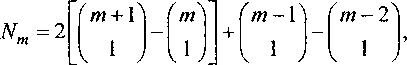
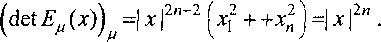
Z(x)A(x) = (Z(x)Af(x),...
ЬфА8 (х), ЕфАДх W, ■ -ДфА8 (х)) =
' Rm(x) .
0 0 ... б''
= (е1(х),.„,ег(х),0,...,0) =
0
. R^^x) 0 ... 0
= 1^ф,
• ^(х) 0 ... 0
• Т(гф 0 ... 0?
где Тф = (ТуДх)).^ . Поэтому, если
и = Аф)5,
то Еф> = Еф^Аф^З - Е№ф)9 = /ф. Ут-
j=r+U
верждение леммы доказано.
Список литературы Полиномиальные решения дифференциальных уравнений в частных производных с постоянными коэффициентами I
- Zweiling, К. Grimdlagen einer Theorie der biharmonishen Polynome/K. Zweiling. -Verlag Technik, Berlin, 1952. -128 p.
- Бицадзе, А.В. К теории гармонических функций/А.В. Бицадзе//Труды Тбилисского университета. -1962. -Вып. 84. -С. 35-37.
- Miles, E.P. Basic sets of polynomials for the iterated Laplace and wave equations/E.P. Miles, E. Williams//Duke Math. Journ. -1959. -V. 26, №1.-P. 35-40.
- Watzlawek, W. Warmpolynome-Modell fur besondere Losungssysteme bei linearen partiellen Differentialgleichungen/W. Watzlawek//Berichte Math.-Statist. Sekt. Forschungszentrum Graz. -1983.-Vol. 211.-P. 1-34.
- Hile, G.N. Polynomial solutions to Cauchy problems for complex Bessel operators/G.N. Hile, A. Stanoyevitch//Complex Variables. -2005. -V. 50, 7-11.-P. 547-574.
- Bondarenko, B.A. Базисные системы полиномиальных и квазиполиномиальных решений уравнений в частных производных/B.A. Bondarenko. -ФАН, Ташкент, 1987. -127 с.
- Pedersen, P. A basis for polynomial solutions to the systems of linear constant coefficient PDE's/P. Pedersen//Advances Math. -1996. -Article № 0005. -V. 117. -p. 157-163.
- Карачик, В.В. О решении неоднородного полигармонического уравнения и неоднородного уравнения Гельмгольца/В.В. Карачик, Н.А. Антропова//Дифференциальные уравнения. -2010. -Т. 46, №3.-С. 384-395.
- Karachik, V.V. Continuity of polynomial solutions with respect to the coefficient of the higher derivative/V.V. Karachik//Indian Journal of Pure and Applied Mathematics. -1997. -V. 28, № 9. -P.1229-1234.
- Карачик, В.В. Построение полиномиальных решений дифференциальных уравнений с постоянными коэффициентами/В.В. Карачик//Дифференциальные уравнения. -1991. -Т. 27, №3.-С. 534-535.
- Никольский, СМ. Граничная задача для полиномов/СМ. Никольский//Труды математического института РАН. -1999. -Т. 227. -С. 223-236.
- Стейн, И. Введение в гармонический анализ на евклидовых пространствах/И. Стейн, Г. Вейс. -М.: Мир, 1974. -331 с.
- Карачик, В.В. О полиномиальных решениях уравнений Ляме/В.В. Карачик//Математические труды. -2002. -Т. 5, № 2. -С. 155-169.
- Ленг, С Алгебра/С. Ленг. -М.: Мир, 1968. -564 с.
- Карачик, В.В. О решении неоднородного полигармонического уравнения и неоднородного уравнения Гельмгольца/В.В. Карачик, Н.А. Антропова//Дифференциальные уравнения. -2010. -Т.46, № 3. -С. 384-395.
- Карачик, В.В. Об одном представлении аналитических функций гармоническими/В.В. Карачик//Математические труды. -2007. -Т. 10, № 2. -С. 142-162.
- Karachik, V.V. Normalized system of functions with respect to the Laplace operator and its applications/V.V. Karachik//Journal of Mathematical Analysis and Applications. -2003. -V. 287, № 2. -P. 577-592.


