Полиномиальные решения дифференциальных уравнений в частных производных с постоянными коэффициентами II

L ( D ) u ( x ) = f ( x )                                          (1)

квадратная и невырожденная. Выберем в теореме 4 из [1] в качестве векторов ^ i ) ( x ) столбцы присоединенной (взаимной) к матрице L ( x ) матрицы L v ( x ). В этом случае V i , R ⁽ i ) ( x ) = det L ( x ) и значит для того, чтобы, воспользовавшись тео^емой 4 из [1], записать п^оизвольное полиномиальное ^ешение системы (1), мы должны найти полиномы P ^{( i )} ( x ) , кото^ые удовлетво^яют у^ав-нению det L ( D ) P ⁽ i ) ( x ) = f i ( x ). Таким образом, решение системы (1) с квадратной, невырожденной мат^ицей, сводится к отысканию полиномиальных ^ешений линейных диффе^енциальных у^авнений вида

L ( D ) u = ^ a _a D ^a u ( x ) = f ( x )                             (2)

k <|a|< q где aa e R, f e P - пространство полиномов и x e Rn. Следует отметить, что уравнение (2) является частным случаем системы (1) при s = t = 1 и, следовательно, к нему применимы все результаты, полученные в [1]. Такой подход к пост^оению полиномиальных ^ешений системы уравнений (1) при s = t является универсальным, но увеличивает порядок дифференциального у^авнения из (1), делая его ^авным степени полинома det L(x) .

Исследуем способы пост^оения полиномиальных ^ешений у^авнения (2). Для этой цели введем следующее необходимое понятие.

Пусть L 1 , L₂ - линейные операторы, действующие на функции f ( x ), принадлежащие множеству X такому, что L_kX с X ( к = 1 , 2) и определенные в некоторой области Q с R n .

Определение 1. Упорядоченную систему функций { f_k ( x ) : к е N ₀ , f_k е X } назовем f -нормированной относительно ( L 1 , Р) в области Q с основанием f ₀( x ), если всюду в этой области

L i f о ( X ) = f ( X ) ; Ц f_k ( X ) = L 2 fk - 1 ( x ) , к е N , x е Q.

Основное свойство f -нормированной системы функций относительно (L1, L2) в области Q состоит в том, что ряд u (x) = ^”=0 fk (x) формально удовлетворяет в Q уравнению L1 u (x) - L2 u (x) = f (x).

Важным частным случаем введеного понятия является L 2 = I , где I - единичный оператор. Тогда f -нормированную относительно ( L , I ) систему функций { f_k ( x ) : к е N ₀ } будем называть f -нормированной относительно L . В этом случае в Q имеют место следующие равенства [10]:

Lf ) ( x ) = f ( x ) ; Lf k ( x ) = f k - i ( x ) , к e N , x е Q.                        ( * )

Более того, если V к , WLf_k ( x ) = LWf_k ( x ) в Q , тогда нетрудно установить, что система функций { w ^k f_k ( x ) : к е N ₀ } будет f -нормированной относительно ( L , W ) в Q .

Пример 1. Пусть L ( D ) линейный дифференциальный оператор первого порядка

д

L (D) = £ ак (x)—, к=1       дxk где ак (x) - аналитические в Q функции, {^к (x): к е N0} - некоторая f -нормированная относительно L(D) в Q система функций и те

W f ( D ) = Z ( - 1) ^кФк ( x ) L ^k ( D ) .

• к = 0

Тогда, существует такая область Q с Q , что для любой аналитической в Q функции F ( x ) справедливы равенства:

L ( D ) W 1 ( D ) F ( x ) = F ( x ) , L ( D ) W ₀( D ) F ( x ) = 0

для x е Q . Оператор W f ( D ) является обобщением известных рядов Ли.

Это утверждение сразу следует из соответствующих результатов по обобщенным рядам Ли [11], если заметить, что при ф _к ( x ) = ф^{к ,!} ( x ) = ^ ( x )/ к !, где L ( D) ф (x ) = 1, система функций { ^ _к ( x ) : к е N ₀ } будет 1-нормированной относительно L ( D ) в Q .

В дальнейшем будем предполагать, что X = Р , Q = R n , и операторы L j ( j = 1 , 2) - дифференциальные операторы в частных произвольных с постоянными коэффициентами. Относительно существования f -нормированных относительно L j ( D ) систем полиномов, в силу теоремы 1

из [1], можем утверждать, что они всегда существуют.

Пример 2. Пусть L(D) = De, где в е N0. Уравнение (2) с таким оператором L(D) - про стейшее из всех возможных. В соответствии с равенствами

D “ x^ex

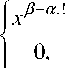
a < в, в $ a система {xkв+a,!: к е N0}, в которой в $ a является 0-нормированной относительно оператора

De системой полиномов, имеющей основание xa,!: Dвxkв+a,! = x(к 1)-в+а,! и Dвxa,! = 0. Кроме того, система полиномов {xa,!: ае N0,в ^ а} составляет базис в kerР(D) nР , поскольку если Dв x“ = 0, то в ^ а.

Ве^немся к у^авнению (2). Для пост^оения его полиномиальных ^ешений воспользуемся основным свойством f -но^ми^ованных систем функций, кото^ое в данном случае выглядит так: п^едположим, что опе^ато^ L(D) как то ^азбит на сумму опе^ато^ов L1(D) и L2(D) и {fk (x): k е N0} - f -нормированная относительно оператора L1(D) система полиномов, тогда фо^мальное ^ешение у^авнения (2) может быть записано в фо^ме то

и ( x ) = £ ( - 1) ^k L ^ (D ) f k ( x ) .                                    (3)

k = 0

Основная п^облема, кото^ую необходимо ^ешить в дальнейшем, состоит в подбо^е опе^ато-^ов L ₁( D ) и L ₂ ( D ) таким об^азом, чтобы ^яд из (3) был не фо^мальным ^ешением у^авнения (2), а его полиномиальным ^ешением и по возможности наиболее общим.

Необходимы некоторые приготовления. Рассмотрим Г0 = {ае N0 : аа Ф 0,| а |= k} - множество индексов оператора Lk (D) младших производных из (2). Обозначим T = Гj-1 \ Г j для j е In-1 и Tn = Гn-1, где множество Г j определяется рекуррентно по формуле Г j = min Г j-1, а операция min задана над множествами B с N0 следующим образом: j min B = {в е B :Vае B, в;< а}. Выберем последовательность натуральных чисел ]k, ..., k } так, t                          j so чтобы множества T были не пусты и Г0 = ^ Tk. Очевидно, что i Ф j ^ Tk, n Tk =0 . Из опре-i=1

деления последовательности { k i } видно, что k s = n . Определим символ MinL k как вектор в — единственный элемент множества T_n . Тогда, каждому множеству T_k i (0 <  i <  s_o ) соответствует в_к. -я компонента вектора в так, что Г _k i - 1 = — = Г _k i - 1 при условии, что k ₀ = 0.

Пример 3. Пусть

L ( D ) =

d ⁵

d ⁵

d ⁵

d x 1 d x 2 d x ₃ d x 4   d x 1 d x 2 d x 3   d x 2 d x ₃d x 4

d ⁶

⁺ d x 46 ’

тогда

Г ₀ = { (1 , 2 , 1 , 1) ; (1 , 2 , 2 , 0) ; (2 , 0 , 2 , 1) } , Г 1 = Г ₂ = { (1 , 2 , 1 , 1) ; (1 , 2 , 2 , 0) } , Г ₃ = { (1 , 2 , 1 , 1) } .

Поэтому T 1 =Г ₀ \ Г 1 = { (2 , 0 , 2 , 1) } , Т ₂ =Г 1 \ Г ₂ = , T 3 =Г ₂ \ Г ₃ = { (1 , 2 , 2 , 0) } , Т ₄ = Г ₃ = { (1 , 2 , 1 , 1) } . Поэтому в нашем случае в = (1 , 2 , 1 , 1), k 1 = 1 , k ₂ = 3 , k ₃ = 4 и Г ₀ = T 1 и T 3 и T ₄, а, следовательно, s_o = 3.

Пусть p е N . Рассмотрим уравнение

K^p ( D ) и ( x ) = ( K 1 ( D ) + K ₂( D ) ) ^p u ( x ) = 0 , в кото^ом K ₁( x ) и K ₂( x ) одно^одные полиномы степени k и к^оме этого полином K ₁( x ) по отношению к x_t имеет минимальную степень большую чем в ₁ , а полином K ₂ ( x ) - однороден по x l степени в ₁ . Определим множества полиномов Л ^ r следующим рекуррентным соотношением:

Л m , r = ( ker K ^r ( D ) n P s ) \ Л m , r - 1 , r >  1 ; Л ^ _д = ker K ( D ) n P_s , в котором s = m + k ( p - 1), а P s - множество однородных полиномов степени s .

Лемма 1. Всякий полином ^ _p ( x ) е Л m _p может быть записан в форме

3 ( m )

^, ( x ) = E ( - 1)

i = 0

Гi + p -1) ■

.^{i       p}     I K 1 ( D ) u i + p - 1 ( x ) ,

V P — I 7

где 3(m) = m + (p - 1)в, a {ui(x): ie N0} - некоторая 0-нормированная система полиномов отно сительно оператора K2(D), удовлетворяющая условию ui (x) e Pm+ik.

Доказательство. Во-первых, необходимо отметить, что по теореме 1 из [1] для любого основания u о ( x ) e ker K ₂( D ) n P _m существует 0-нормированная относительно K ₂( D ) система полиномов такая, что u i ( x ) e P _{m +} ik . Определим полином S^ n^p ) ( x ) следующим равенством:

S np ) ( x ) = ( n ⁺ p -4 K П ^{+ 1} ( D ) u n + p - 1 ( x ) ■

V p — 1 7

Пусть полиномы У _г ( x ), 1 <  r <  p определяются из равенства 3 ( m )     i + + r -

У г ( x ) = E ( - 1) i           I K 1 ( D ) u i + r - 1 ( x ) ■                                (5)

£0 I r-1 7

0сно, что yp (x), найденный по этой формуле, совпадает с (4). Тогда для r > 1 можно запи- сать

)     ..++r-

K(D)Уг(x) = (K1(D) + K2(D)) E (-1)i      Л  IK1(D)ui+r-1(x) = i=0       I r-1 7

8 ( m )

= E (-1) i i=0

V

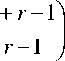
8 ( m )

Ki+1(D)ui+r-1(x) + E (-1)i i=0

(

Г i + r -1) i

I K i ( D ) u i + r - 2 ( x ) =

V r-1 7

3 ( m ) + 1

= E (-1)i-1

i = 1

V

i + r - 2 r - 1

3 ( m )

Ki(D)ui+r-2(x) + E (-1)i i=0

Г i + r -1) ;

I K 1 ( D ) u i + r - 2 ( x ) =

V r -1 7

( - 1) ^{3 ( m )}

3

Г i + r - 2) ■

_Л bK1 (D)ui+r-2(x) =

V r-1 7

8 (m)      (; + r - 27

= (-1)3(m)S((m)(x) + E (-1)i I          IK1 (D)ui+r-2(x) = (-1)3(m)S(rm)(x) + yr-1(x)■ i=0       V r 2 7

Аналогично, при r = 1 можно найти

3 (m)

K(D)y(x) = (K 1(D) + K2(D)) E (-1)iKi(D)ui(x) = E (-1)iK 1+1(D)ui(x) + i=0

3 (m)                           3 (m)                           3 (m)—1

+ E (-1)iKi (D)ui-1(x) = E (-1)iK\+1(D)ui (x) - E (-1)iK\+1(D)ui (x) = i=1                                  i =0

= (-1)³⁽m) S^m)(x)■

Далее следует заметить, что для r < p верны рассуждения snp)(x) = 0 ^ K 1n+1( D) un+p-1( x) = 0 ^

^ 0 = K2^p-r (D)Kn⁺¹(D)un+p-1(x) = K1ⁿ⁺¹(D)un+r-1(x) ^ Sn(^r)(x) = 0.

Поэтому для выполнения условий

K(D)УГ (x) = yr-1(x), 2 < r < p; K(D)У1(x) = 0, необходимо, чтобы S(p7)(x) = 0. Поскольку степень полинома un+p-1(x) по переменной xl равна m + (n + p -1)el, а оператор K 1n+1(D) снижает степень полинома по переменной xl не меньше чем на el +1, то степень полинома K 1n (D)un+p-1(x) по переменной xl не больше, чем m + (n + p -1)Pl - n(Pl +1) = m + (p -1)Pl - n . Если n выбрано так, что m + (p -1)Pl < n, то Snp)(x) = 0. Поскольку 3(m) = m + (p-T)Pl, то S(p,m)(x) = 0. Кроме этого, общая степень полино-

Карачик В.В.                        Полиномиальные решения дифференциальных уравнений в частных производных с постоянными коэффициентами II ма Д, (x) равна m + k(р -1). Далее, так как K (D)Ф(x) = $р_i(x) ^ 0 для i = 0,1,..., р _1 (первый член в сумме (5), через которую представляется полином ^р_i (x)) обладает наибольшей по xl степенью и равен up _ i _1 ^ 0) и Kp (D )#р (x) = 0, то справедливо включение ^р (x) е Л mm р .

Убедимся, что линейная независимость полиномов u01)(x) и u02)(x) (это основания соответствующих 0-нормированных систем) приводит к линейной независимости полиномов и(^ix) и ир2)1(x). Действительно, если полиномы ир1._1(x) и ир2_)1(x) линейно зависимы, то Ba,ве R , au(р_1(x) + виР2)1(x) = 0 ^ Kр_1(D)(auр1_1(x) + вир2)1(x)) = 0 ^ au01)(x) + ви02)(x) = 0, т.е. полиномы и01)(x) и и02)(x) линейно зависимы. Противоречие. Значит, и(2,(x) и ир2_)1(x) линейно независимы. Из этого, в свою очередь, следует линейная независимость полиномов ^Р\ x) и $р2( x), поскольку в сумме (4) только первые слагаемые ир^x) и ир2)1(x) имеют старшую степень по переменной xl, и они линейно независимы. Следовательно, dim Л ;m, р > dim (ker K 2( D) n Vm).

Если обозначить

1_Л = dim ^ (ker KA (D) \ ker K^ (D)) Q Vs), где s = m + k(р_ 1), тогда, используя предложение 1 из [1], нетрудно получить ( s _ k (Л _ 1) + n _ 1^ ( s _ kA + n _ 1^

Л =                        I _           1 I.

V n _ 1      ) V n _ 1    )

0сно, что 1р = Лmm р . Так как подстановка Л = р в предыдущее равенство дает lp

^ s _ k (р _ 1) + n _ 1

_

V

n _ 1

^ s _ kp + n _ 1

, n _ 1

^ m + n _ 1

_Vn _ 1

_

(m _ k + n _ 1

n _ 1

= dim(ker K₂( D) n V_m),

то неравенство (7) превращается в строгое равенство. Поэтому, если выбрать в (4) вместо и₀(x)

базисные полиномы из ker K₂(D) n V_m , то полиномы $_р (x) будут базисом в Л^s_{m р} . 4тобы завершить доказательство остается заметить, что почленная линейная комбинация двух 0 -нормированных относительно одного и того же оператора систем полиномов будет также 0-нормированной системой полиномов относительно этого же оператора. Лемма доказана. □

Предложение 1. Пусть операторы K1(D), K2(D) и K(D) такие, как описаны в лемме 1. Тогда для любой 0-нормированной относительно оператора K (D) системы полиномов {^- (x): i е N0}, удовлетворяющей условию ^i (x) е Vm+ik , и натурального числа n существует 0-нормированная относительно оператора K2(D) система полиномов {ui (x): i е N0} такая, что m+sPi      i+ + sA

^s (x) = ^ (_1)i       I Ki (D)Ui+s (x)                               (8)

i=0        V ^s )

для s = 0,1,^, n .

Доказательство. Поскольку ^_n (x) е V_m+kn и ^_n (x) - элемент множества {^- (x): i е N₀}, то по лемме 1 найдется 0-нормированная относительно оператора K₂(D) система полиномов {ui(x): i е N₀} такая, что выполнено равенство (8) при s = n. Принимая во внимание, что по лемме 1 верны равенства K(D)^_s(x) = ^_s_1(x) для s > 1 и K(D)^₀(x) = 0 завершаем доказательство.

□

Предложение 2. Пусть K(D) = K1(D) + K₂(D). Если оператор K1(D) не однороден и наименьшая степень производных, входящих в него, больше а - порядка однородного оператора

K2(D), то всякое полиномиальное степени m решение уравнения K(D)v(x) = 0 может быть записано в виде m v (x) = £ (-1) iKi (D) Ui (x),                                      (9)

i=0

где {ui (x): i e N₀} - некоторая 0-нормированная относительно оператора K₂(D) система полиномов такая, что ui (x) e Pm_+ia.

Доказательство. Заметим, что формула (9) совпадает с формулой (3), записанной для уравнения K(D)v(x) = 0 (L1 = K2, L2 = K1), если Kl (D)ul (x) = 0 при l > m. Последнее же очевидно выполняется и значит (9) задает решение уравнения K(D)v(x) = 0 . Согласно предложению 1 из [1] имеем равенство dim(kerK(D) nUm) = dim(ker K2(D) n Um), где Um - пространство полиномов степени m [1]. Поскольку линейная независимость полиномов u01)(x) и u02)(x) (основания соответствующих 0 -нормированных систем) ведет к линейной независимости по старшему члену полиномов v(1)(x) и v(2)(x) из (3), то базис в ker K2(D) n Um порождает по формуле (9) базис в ker K(D) n Um. Разложим по этому базису v(x) - произвольное полиномиальное степени m решение уравнения K(D)v(x) = 0. Имеем v(x) = £ j «jv(j)(x). Тогда, если обозначить ui (x) = £ j ajuij) (x), то будем иметь mm v (x) = £ av (j)( x) = £ a £ (-1) iK’ (D) u,(- j)(x) = £ (-1) iKi (D )£ aju^ j)(x) = . j                       j       i=0                                   i=0                     j

= £ (-1)iKi(D)ui(x), i=0

причем K₂(D)u₀(x) = K₂(D)£ j. aju0 j)(x) = 0 и

K2(D)ui (x) = K2(D)£ jj)(x) = £ aju ^j)(x) = ui-1(x). jj

Искомая 0-нормированная система {ui (x): i e N₀} полиномов относительно оператора

K₂(D) построена. Доказательство завершено. □

Рассмотрим дифференциальные операторы Is (D) и Ji (D), определяемые равенствами so

Is (D) = £ Ji (D),  Ji (D) = £ aaD^a.

i=s                        aeTki

Пусть {p^j)(x): i e N₀} при j = 1,^, N_m набор 0-нормированных относительно оператора

Is (D) систем полиномов, удовлетворяющих условию ti-i^j)(x) e P_m+ik с основаниями г?0^j)(x), образующими при j = 1,^, N_m базис среди полиномиальных степени m решений уравнения Is (D)v(x) = 0. Очевидно, что по теореме 1 из [1] такие системы всегда существуют.

Введем полиномы u j (x), определяемые из равенства a (m)

uj(x) = £ (-1)i(L(D) - Is(D))'tii^{( j})(x),                               (10)

i=0

где      a( m) = m + 31( m) + + 3_s-1( m)      и      3j (i)      определяются рекуррентно:

3j(i) = m + P_k, (i + J1(i) + + 3j-1(i)) для j > 1, а J1(i) = m + в_к1i. 0сно, что a(m) = a(m)m=1 m , поскольку        J1( m) = m + в_к1m = (1 + в_к1) m = J1( m )m=1 m        и        по        индукции

5j (m) = m + Pkj (m + ^^(m) + — + 5j-1 (m)) = 5j (m)m=1 m .

Карачик В.В. Полиномиальные решения дифференциальных уравнений в частных производных с постоянными коэффициентами II

Теорема 1. Максимальная система линейно независимых по старшему члену полиномиальных степени m решений однородного уравнения (2) (f (x) = 0) может быть определена в виде {Uj (x): j = 1, .... N_m}, где Uj (x) находятся из (10).

Доказательство. Пусть J₀(D) = L(D) - Lk (D). Разложим оператор L(D) в следующую сумму операторов:

5-1

L(D) = E Ji (D) + I, (D).

i=0

Обозначим

Ki( D) = Jt (D), K 2( D) = Ji+i (D) + - + Js-i (D) + I, (D), где s > l > 1 и s > 1. Заметим, что полиномы K 1(x) и K2(x) удовлетворяют всем требованиям леммы 1 и поэтому мы вправе использовать предложение 1. Воспользовавшись равенством (8) s -1 раз при l = 1, ..., s -1 устанавливаем, что для произвольной 0-нормированной относительно оператора J 1(D) +-----+ Js-1(D) + Is (D) системы полиномов {wi (x): i е N0}, удовлетворяющих ус ловию wi (x) е Pm+ik и натурального n найдется 0-нормированная относительно оператора Is (D)

система полиномов {^- (x): i е N₀} такая, что

Wi (x) = E (-1)^|ils-1

'р-.is-1

Pil11

I 1 J

'¹i¹s-¹'

V is-1 J

J i-c D)-J^( D ^ i_{s ч}( x),

где i = 0,..., n , | ilj = i + i1 +-----+ ij, причем | i 1₀= i, а суммирование ведется по всем i1,..., i_s-1 из N₀

удовлетворяющим неравенствам ij<m +1ilj-1 0k_j , jе I_s-1. Отсюда нетрудно получить, что

Yi (m)

wi (x) = E (-1) k E k = 0          l i l s-1 = k

<1 .1 Л l i1

V i J

l П s-1

I 1

V s-1 J

J i4 D)-J^

(D )A+k (x),

где Yi (m) = 51(m) +-----+ 5_s4(m) и, следовательно, поскольку

E •         •     J 1(D) Js-1(D) =    E i i , • ,    , •         । 1(D) Js-1(D) = lisГ=k V i1 J V is-1 J                            i1 +-+ts-1= k i!i1!      (i + i1 + - + is-2)!is-1!

= у   (i+i^+^+i,-¹)!Ji1(D)-Ji D) = (i+k)!   у   —k^_Ji D)-Ji^s-D) =

,1+...E-1=k     i-i1!-is-1!       1           s-1           i!k! ^-E-1=k Ч'-is-1!              s- i + kY

=    . I (J 1( D) + - + Js-1( D)) k,

V i J будем иметь

Wi (x) = ^Yj^m     k f i + k 1 (J 1(D) + - + Js-1(D))^k^.+k(x).                     (11)

k=0 V k J

Если L(D) = L_k (D), то вычисляя

Y0^{( m})

u(x) = W0(x) = E (-1)k(J 1(D) + - + Js-1(D))k^k(x), k=0

можно перейти к доказательству после формулы (13). Если же оператор L(D) имеет степень больше k , то воспользуемся предложением 2, а именно формулой (9), при

K 1( D) = J 0( D), K 2( D) = J 1( D) + - + Js-1 (D) + Is (D).

По этой формуле для любого u (x) - полиномиального решения однородного уравнения (2) найдется соответствующая 0-нормированная относительно оператора L(D) - J0(D) система полиномов {wi (x): i е N0}, которая в свою очередь может быть задана системой {^- (x): i е N0}, та- кая, что u (x) = E (-1) jJ0 (D)Wj (x). .j=0

Подставляя сюда wj (x) из (11) и учитывая при этом, что Yi (m) < Ym(m) для i < m (увеличивая верхний предел в сумме из (11) мы добавляем в сумму лишь нулевые члены) и а(m) = m + ym (m), получим m            Ym(m)     ( j + p, u (x) = E (-1) jJ 0 (D) E (-1) k       I (J 1( D) + - + Js-1( D)) k^i+k (x) =

.j=0                k=0

Om)

= E (-1)i E , IJ0^j (D)(J 1(D) + - + Js-1(D))^ (x)■ i=0       j+k=i V ^k)

Отсюда сразу находим

a( m)

u(x) = E (-1)i(J0(D) + J 1(D) + - + Js-1(D))iA(x)■                     (13)

i=0

В силу леммы 1 линейная независимость полиномов г?® (x) и ^(2) (x) — оснований соответствующих 0-нормированных систем влечет за собой линейную независимость полиномов w01)(x) и W (x) из формулы (11), а из этого следует линейная независимость полиномов u(1)(x) и u(2)(x), находимых по формуле (12), поскольку в сумме (12) первые слагаемые w01)(x) и w02) (x) имеют наибольшую степень, а они линейно независимы. Поэтому, учитывая что в соот ветствии с предложением 1 из [1] Nm (n, k) - максимальное число линейно независимых по старшему члену полиномиальных степени m решений однородного уравнения (2) равно числу базисных полиномиальных степени m решений уравнения Is (D)v(x) = 0, т.е. Nm(n, k) = Nm, то система полиномов {u, (x): j = 1, —, Nm} является максимальной системой линейно независимых по старшему члену полиномиальных степени m решений однородного уравнения (2). Доказа тельство теоремы завершено. □

Замечание 1. Значение а(m), вычисленное для некоторых конкретных примеров оказыва ется довольно завышенным, поскольку в теореме оно служит лишь для доказательства того, что u j (x) - полином.

Пример 4. Пусть L(D) = L2 (D) = А. Используя теорему 1, найдем связь между гармоническими полиномами от n переменных и гармоническими полиномами от n -1 переменной. В соответствии с определением вектора в = MinL2 найдем в = (0,—, 0,2), ki = i и поэтому P_k, = 0, 81(m) = m . Выберем s = 2 и поэтому 1₂(D) = А = А-d²/dx1², а(m) = 2m . 4тобы использовать теорему 1 мы должны найти такие 0 -нормированные относительно А системы полиномов, чтобы их основания образовывали базис в ker АпP_m.

По формуле (11) из [1] находим максимальное число линейно независимых однородных сте-

I m+n-1 I | m-2+n-1 I пени m гармонических полиномов от n переменных Nm(n,2) = I     I-I I (s = t = 1, m           I n-1 ) I n-1 )

Vm = {0}). Проверим, что системы полиномов {hsj (.x)xm-s,!: i e N0}, где j = 1,—,Ns (n -1,2), s = 0,—, m , xc = (x2,—, xn) и

IT

hs j(x) =

Hs (x),

(2,2) i (n -1 + 2 s, 2) i

(a, b)k = a(a + b)(a + kb - b) - обобщенный символ Похгаммера (при соглашении (a, b)0 = 1), а система полиномов {Hs(xc): j = 1,—,Ns(n-1,2), s = 0,—,m} образует базис в однородных гармо- нических полиномах степени s от n -1 переменной являются 0 -нормированными относительно А . Действительно, поскольку А||x||mHS(x) = m(m + 2s + n-2)||x||m 2 Hs(x), где Hs(x) - однород ный гармонический полином степени s , то вычисления показывают что

AhSjj (x) =

2i (2i + 2s + n - 3) ц_|pi-2 (2,2)i(n -1 + 2s, 2)i^l|x|1

H/( x) =

II xГ -² (2,2) i-i( n -1 + 2 s, 2) i-i

hs (x) = Ahi-j x).

Кроме этого, AhS j (x) = 0. Значит, системы полиномов {Д j (x)xm s,!: i e N0} являются 0- нормированными относительно оператора А. Рассмотрим основания этих систем hS j (x)xm-s,! = xm-s,!Hsj (x) при j = 1,..., Ns (n -1,2) и s = 0,..., m . Поскольку mm

0 = AP(x) = AУ xm-SPs (x) = У xm-s APs (x) ^ APs (x) = 0 ^ Ps (x) = У Cs, H (x) ^ s=0                s=0                                                 j mm

^ P (x) = У xm-SPs (x) = У xm-s У Cs, jHS( x) = У (m - s)! Cs, jxm-s,! Hj( x), s=0                   s=0         j                     s, j то основания систем hS, j(x)xm-s,! образуют базис в ker AnPm. Поэтому по теореме 1 произвольный однородный гармонический полином от n переменных степени m может быть представлен как линейная комбинация полиномов вида (10)

a(m)                                [(m-s)/2]                     II x|²i xm-s,!

^u(,)=-^(a-a)...x>= £ (-i)D(2,2),(n_;+2s,2),Hs⁽-=

[(m - s) / 2]

= У  (-1)i i=0

2i  m-s-2i,!

^xll   ^x1

(2,2) i (n -1 + 2 s, 2) i

Hs (x) = Gm _ s (x) Hs (x),

где обозначено

[ k / 2]

G (x) = У (-1)i i=0

|| x|²i xk^-2i'^!

(2,2) i (n -1 + 2 s, 2) i

а H_s (.x) - произвольный гармонический полином от n -1 переменной.

Итак, для того чтобы из однородного гармонического полинома от n -1 переменной Hs (.x) получить однородный гармонический полином от n переменных Hm (x) необходимо его умно жить на полином Gm _ s (x) из (14). Если взять базисные гармонические полиномы {Hsj (.x): 0 < s < m} степени m от n -1 переменной, то система полиномов {Gmm-s(x)Hsj(.x): 0 < s < m} будет базисом в однородных степени m гармонических полиномах от n переменных. Это соответствует замечанию 1 из [1].

Рассмотрим неоднородное уравнение (2), в котором f (x) - однородный полином степени l.

Теорема 2. Любое полиномиальное степени l + k решение уравнения (2) может быть представлено в виде

а( k+1)

u (x) = У (-1)i (L(D) - Is (D))i^. (x),                              (15)

i=0

где система полиномов {^- (x): i e N₀} - некоторая f -нормированная система полиномов относительно оператора I_s (D), удовлетворяющая условию ^i (x) e T^>_{1+k (}i₊₁₎.

Доказательство. Заметим, что если иметь в виду формулу (13) из теоремы 1 при m = k +1, то достаточно доказать представление хотя бы одного частного решения уравнения (2) в виде (15). Действительно, если {wi(x): ie N₀} - некоторая 0-нормированная система полиномов, задающая по теореме 1 произвольный полином u₀(x) e ker L(D) n T^>_1+k по формуле (13), то система

{wi (x) + $i (x): i e N₀} такая, что wi (x) + ^i (x) e T₊k₍i₊₁₎ будет f -нормированной системой полиномов относительно оператора Is (D), т.е.

Is (D)(Wi (x) + ^ (x)) = Wi -1( x) + A-1( x); Is (D)(Wo( x) + t%( x)) = Is (D W x) = f и, значит, будет верно представление вида (15)

uo(x) + u (x) = £ )(-1) i (L(D) - Is (D))W (x) + i=0

a (k+l)                                        a (k+1)

+ £ (-1)i (L(D) - Is (D))^ (x) = £ (-1)i(L(D) - Is (D))i(wi (x) + A(x)). i=0                                            i=0

Пусть {^- (x): i e N₀} - система полиномов f -нормированная относительно оператора Is (D), удовлетворяющая условию ^i(x) e T_+k(i₊₁). Очевидно, что такая система существует. Тогда для полинома u(x), определяемого по формуле (15), аналогично (6) будем иметь

L(D)u (x) = (L(D) - Is (D) + Is (D)) £ ) (-1)i (L(D) - Is (D))^ (x) = i=0 a (k+1)                                          a (k+1)

= £ (-1) i (L(D) - Is (D)) i/- (x) + £ (-1) i (L(D) - Is (D))'^-1(x) + f (x) = i =0

a (k+1)                                          a (k+1 )-1

= f (x) + £ (-1) i (L(D) - Is (D))iм (x) - £ (-1)i (L(D) - Is (D))iм (x) = i=0

= f (x) + (-1)^a(k+l) (L(D) - Is (D))"⁽k⁺l⁾⁺X(k+1) (x).

Поэтому, если выполнено равенство

(L(D) - Is(D))“(k+l)+X(k+1) (x) = 0, то формула (15) будет задавать полиномиальное решение уравнения (2). Равенство же (16) легко следует из определения величины а(m), так как для того, чтобы было выполнено равенство

(L (D) - Is (D) )а(m )+Х (m)( x) = 0, не имеет значения является ли система {^- (x): i e N0} 0-нормированной или нет, а важно лишь включение ^i (x) e Tm+ik (см. лемму 1 и теорему 1). Доказательство завершено. □

Приведем более простой способ построения решения неоднородного уравнения (2) с полиномиальной правой частью f (x), вытекающий из теоремы 2. Пусть полином f (x) представляется в форме f (x) = £а faxa,!, а полиномы ^а (x) при тe N0 имеют вид а (|ст|)

^Т (x) = £ (-1) iLi (D) x^e+CTJ

,

i=0

где в eA = ^min— min Г_о : п e SV, Г₀={а e N q : a_a ^ 0,| a |= k}, a_a - коэффициенты оператора ^ п(1) п(n-1)^{1                                  J}

L(D), S_q - симметрическая группа, а оператор L(D) определяется равенством

L (D) = £ (a_a I ap) D^a.

а * в

Базисность системы полиномов {^Т(x): в ^ Т,Тe N0} устанавливает следующее утвержде- ние.

Предложение 3. Пусть u(x) - некоторое полиномиальное решение уравнения (2), тогда найдутся такие числа С_Т, что имеет место равенство

u^(x) = £ (^fa^{1 a}p)^z+в^(x) ⁺£ cg^g^(x).                        ⁽¹⁷⁾

a                P^g

Доказательство. Пусть р е Л. Разделим обе части уравнения (2) на коэффициент ар, поскольку ар Ф 0. Очевидно, что перенумерацией переменных можно добиться того, чтобы Р = MinLk . Согласно определения so имеем J_s (D) = D^p. Воспользуемся примером 2. По нему система полиномов {x^kp+а,!: kе N₀,р ^ а} является 0-нормированной относительно оператора

D^p, т.е. D^px^kp+а,! = x^(k 1)^р+а,! и D^px“' = 0, и имеющей основание х“'. Эти основания составляют базис в ker L(D) n Р. Поэтому на основании теоремы 1 система полиномов

(?У(x) :| с |= m,Р ^ с}, находимых по формуле, являющейся частным случаем формулы (10), об-

^азует максимальную систему линейно независимых по ста^шему члену полиномиальных степени m решений однородного (f (x) = 0) уравнения (2). Далее, так как система полиномов

{x⁽k+1)^р+а,'-^ k е N₀} является x“' -нормированной относительно оператора D^p, то по теореме 2

полином ^_а+р (x) является решением уравнения

^ (а_а/ар)D^au(x) = x^a,!, k<|а|< q

• а, значит, уравнения (2) при f (x) = apx^а,!. Поэтому полином следующего вида ^_а(f_a/ар)ia_a+р(x) является частным решением уравнения (2) для заданного f (x). Доказатель-

• ство завершено. □

Пример 5. Множество Л для двух основных операторов математической физики D^ - Д и Д совпадает с множеством индексов Г(L) = {ае N0 : а_а Ф 0} их ненулевых коэффициентов. Если L(D) = D^ - Д, тогда можно положить р = (2,0, _, 0) и поэтому L(D) = -Д . В этом случае решение (17) при f (x) = 0 может быть преобразовано к известной форме [12]

то

то

и(x) = £ t^2k,!Д^kp(x) + £ t^2k+1'д^kQ(x), k=0                k=0

где P(x) и Q(x) - некоторые полиномы от x е Rⁿ.