Поляризация вакуума квантованного скалярного поля при ненулевой температуре на фоне кротовой норы с бесконечно короткой горловиной

Интерес к эффекту поляризации вакуума, в сильных гравитационных полях связан, в основном, с исследованием ранней Вселенной и построением самосогласованной модели испарения черных дыр. Этот эффект описывается полуклассической теорией гравитации

G^ = W^ren,                             (I)

где hT^ren вакуумное среднее оператора тензора энергии-импульса квантованных полей. Отметим, что вакуумные флуктуации квантованных полей рассматривались в качестве материи, обеспечивающей существование кротовых пор в работах [1 -4] .

Основная трудность теории полуклассической гравитации состоит в том, что эффекты квантования гравитационного поля игнорируются. Популярное решение этой проблемы — это предел большого числа, материальных полей, при этом вкладом гравитационного поля можно пренебречь по сравнению с вкладом в правую часть уравнений ( I) других квантованных полей. Другая проблема. такой теории заключается в том, что эффекты поляризации вакуума, определяются, как правило, топологическими и геометрическими свойствами пространства-времени в целом и выбором

* Работа выполнена в рамках реализации программы развития Научно-образовательного математического центра Приволжского федерального округа, соглашение Я⁹ 075-02-2022-882.

квантового состояния, в котором вакуумные средние вычисляются. Это означает, что вычисление функциональной зависимости (TViren от метрического тензора, который должен быть определен из уравнений ( I ), представляет огромную трудность. Только в некоторых пространствах-временах с высокой степенью симметрии для конформно инвариантных полей (T_vv iren такие вычисления были проделаны, а. уравнения ( I ) решены [5 -9] .

Численные вычисления (T^ren обычно чрезвычайно трудоемки [10-17]. В некоторых случаях (T^viren определяется локальными свойствами пространства-времени, и можно приблизительно вычислить функциональную зависимость (T^viren от метрического тензора. Одним из наиболее широко известных примеров такой ситуации является случай весьма, массивного поля. В этом случае масса поля m много больше 1/1, где 1 — характерный масштаб кривизны пространства- времени

1 ml

(П)

и (T^ren можно разложить по этому малому параметру [18 -24] .

Также были проведены приближенные вычисления (T^} для безмассовых квантованных полей, пекопформпо связанных с кривизной пространства-времени. Примерами таких вычислений в статических пространствах Эйнштейна ( R_vv = Kg^ являются приближения Пэйджа, Брауна и Оттевилла. [25 -27] . Эти результаты были обобщены на. произвольные статические пространства-времена Занниасом [28] . Другой подход к получению приближенных выражений для (T^} для конформно связанных с кривизной безмассовых полей в статических пространствах-временах был предложен Фроловым и Зельниковым [29] . Их расчеты основывались, главным образом, на. геометрических аргументах и общих свойствах тензора, энергии-импульса, а. не па. теории поля. Позднее, с использованием методов квантовой теории поля, Андерсоном, Хичкоком и Самуэлем были получены выражения для (у²i и (T^i квантованного скалярного поля в статических сферически-симметричных асимптотически плоских пространствах-временах [10] . Опи предполагали, что поле может находиться в вакуумном квантовом состоянии с пулевой или ненулевой температурой, может быть массивным или безмассовым и иметь произвольную константу связи £ поля с кривизной. Их результат был представлен в виде суммы двух частей: численной и аналитической

(Tviren

µ

( v inumeric

+ ^(Tv i analytic -

(Ш)

Аналитическая часть этого выражения сохраняется. Опа имеет след равный следу конформной аномалии для конформно инвариантного поля. По этой причине было предложено использовать (TVianaiytic ^как приближение для (T^iren. Аналогичный результат был получен Гровсом, Андерсоном и Карлсоном [30] в случае безмассового поля со спином равным 1/2 в статических сферически симметричных пространствах-временах.

В [31] (TViren получен для массивного скалярного поля с произвольной связью с гравитационным полем точечного глобального монополя. В этой работе использовалось приближение Швингера-Девитта, до второго порядка, малости по параметру ( II) .

Подчеркнем, что единственным параметром размерности длины в задаче (I) является план-ковская длина 1Р1. Это означает, что характерный масштаб 1 кривизны пространства-времени (который соответствует решению уравнений (I)) может отличаться от 1Р1 только при наличии большого безразмерного параметра. В качестве примера, такого параметра, можно рассмотреть число полей, поляризация которых является источником искривления пространства-времени1. В случае массивного поля существование дополнительного параметра 1/m размерности длины не увеличивает характерный масштаб кривизны пространства-времени 1, который соответствует решению уравнений (I)2. Для безмассовых квантованных полей таким параметром могут быть константы связи поля с кривизной пространства-времени [4]. Другой возможностью введения дополнительного параметра, в задачу (I) является рассмотрение ненулевой температуры квантового состояния для квантованного поля. Известно (см., например, [32]), что в высокотемпературном пределе (когда. T ^ 1/l, T — температура теплового квантового состояния) (Тф) для такого теплового состояния пропорциональна четвертой степени температуры T.

В этой работе получено приближенное выражение для (ф2)геп квантованного скалярного поля в пространстве-времени кротовой поры с бесконечно короткой горловиной в предположении о том, что поле является безмассовым, имеет произвольную связь со скалярной кривизной просранства-времени и находится в тепловом квантовом состоянии с произвольной температурой.

На протяжении всей работы будут использоваться система единиц, в которой ~ = c = G = кв = 1

1.    Неперенормированное выражение у2^

Метрика, статического сферически симметричного пространстве-времени кротовой поры с бесконечно короткой горловиной, аналитически продолженная в евклидово пространство, имеет вид ds2 = dT2 + dp2 + (|р| + a)2(d62 + sin2 6 dp2),                         (1.1)

где т — евклидово время (т = -it, где t координата, соответствующая времениподобному вектору Киллипга, который всегда, существует в статическом пространстве-времени).

Вакуумное среднее оператора ф² квантованного скалярного поля ф может быть вычислено с использованием метода раздвижки точек [33, 34] из евклидовой функции Грина G e (x; x) следующим образом

(^{ф (x}, ^x)iunren    GE ^(x,X),                                     (l-^)

где G e (x,X) удовлетворяет уравнению

[□x - №)] G e (x,x) = - ^(=4, V |g^(x)|

(1.3)

□_x = g^^v (x)V_MV_v вычисляется для метрики ( 1.1 ). £ — константа, связи скалярного поля ф с

кривизной R пространства-времени. В пространстве-времени ( 1.1) можно записать

5(т - T)5(r, г)5(П, П) ^2

5⁴(x, X) V g^(x)

как

. Дельта-функция 5(П, П) может быть разложена по полиномам Лежандра Pi

∞

5(П, П) = X Yim №т(П) = - X(2l + 1)Pi(cos Y),                (1-4)

l,m                          l=0

~

~

~.

где cos y = cos 6 cos 6 + sin 6 sin 6 cos(ф — ф).

В этой работе предполагается, что поле находится в вакуумном состоянии с ненулевой температурой, определяемом по отношению к времениподобному вектору Киллипга. В этом случае функция Грина является периодической по т — Тс периодом —, где T — температура поля. В этом случае 5(т — Т) имеет вид

∞

5(т - Т) = T X

ein2nT (т—Т)

(1.5)

n= — ^

Тогда.

GE (x; X)

∞

^T          in2nT (т -

4П ^ e n=-^

∞

) X(21 + 1)P(cosY)gnl(р,Р) = i=o

T ^∞

— 52 ⁽²l ^{+ 1)p}i^(cos y) gol⁽р^{,р) +}

4n -‘^ i=o

T∞             ∞

+ 2П X cos[2nnT(т — Т)] X (21 + 1)Pi(cos7) gnl(р,р), n=1                   i=o

(1.6)

где gni(p,p) удовлетворяет уравнению

d2         2 d(|р| + a) d dр‘2 (|р| + а) dр dр

(2nnT)2 +   +   + №

5⁽р, ^р) (|р| + a)² .

(1.7)

Используя результаты работы [35] , получим при р> р, n = 0

K_v ( k(a + ри I_v ( k(a ^gnl(р,^р ) = p        ==

( а + р )( а + р )

(8^ — 1)Iv (x)Kv (x) + x^Iv (x^Kv (x) + Iv (x)K^ (x)^ (8^ — 1)K2(x) + 2xKv (x)Kv (x)

Kν

V ⁽a ^{+ p)(}a ⁺ р)

(1.8)

Представим gni (р, р) в виде

gni ⁽Р, ^р) = gM ⁽Р, ^{р) +} gn ⁽р^,р),

(1.9)

где

gM ⁽р, ^р) =

g^O,р) =

K_v ^k(a + р) J Iv ^k(a + р) J

V ⁽a ⁺ р^{)(а +} p )

(8^ — 1)Iv (x)Kv (x) + x^I_v (x)Kv (x) + Iv (x)K_v (x)^

(8^ - 1)K2 (x) + 2xK(x)K(x)

K^(a + р)^ K^(a

VTa+g^Ia+p)

Решение уравнения (1.7) при n = 0, р > р имеет вид

goi ⁽р, Р) = gM ⁽р, ^{р) +} goi ⁽р,р),

(1.Ю)

где

g ₀ ^M _i ( р, р ) =

(р + а) ^(l+1)(р + а)

21 + 1

,

gI ⁽р^,р ) =

a2i+1(1 - 8£)(р + а)

l-1(р + a)-i-1

2(21 + 1)(1 — 4^ + 1)

В дальнейшем будем считать 9 = 9, примет вид

р = ф. В этотI случае cos(y) = 1 ii Pi (1) = 1- Тогда. ( 1.6 )

∞

GE ( x ; x )

T∞              T∞

52 ^{(21 +} 1) goi ⁽р, ^{р) +}     52 ^{cos[ 2nnT (}'

4п                     2п

i=o

∞

(т — Т)] X (21 +1) gnl(р,^p). (ТИ) i=o

Представим Ge (x; X) в виде где Ge0(x; X) есть первая сумма в (1.11), a GEn(x; X) последняя двойная сумма в (1.11). Представим также каждое из этих слагаемых в виде

G _E0 (x; X) = GM₀(x; X) + G E ₀ (x; X). n = 0.

GEn (x; X) = GMn (x; X) + GEn(X; X). n = 0.

(1.13)

а определения GM (x; X). G E0 (x; X). GM_n(x; X) и GEn(x; X) даны ниже. Определим

GMn^(T,p;^т,р)

∞∞

_2п X cos [^{2nnT(т - т)}] X ⁽²l ⁺ 1) gM ⁽р. ^р).

(1.14)

Используя теорему суммирования для функций Бесселя

1 = 0

[36] и выполнив суммирование по n в

(1.14) , получим при т

GMn(p; р)

- тр = 0

T

4п²(р — р)²   4п(р — р)

T2

+ 12

T ⁴п²(р - р)²

----180----+ О((р - р) )

(1.15)

Тогда определение GEn(T. р; т.р) имет вид

GEn^(T. р; ^т.^р)

T∞             ∞

^- 2n X ^cos [^{2nnT (т - т)}] X ⁽²l ^{+ 1)}дП1⁽р.^р) = n=1                    1=0

х

~                ~      K k(a + р) K k(a-

- X cos ■  /(т - 5) 1 X (2l + 1)   ^k

2n n=1               E            .

(8€ - 1)IV(ka)Kv(ka) + ka^Iv(ka)Kv(ka) + Iv(ka)Kv(ka))

х

(8€ - 1)K2(ka) + 2kaKV(ka)Kv(ka)

(1.16)

Следовательно

GEn^(T. р; ^т. ^р) = GMn⁽p; ^{р) +} GEn ^(т. р;^т. ^р =

T                         p

T

4п²(р - р)²   4п(р — р)

T2

+ 12

T ^               ~      K k(a + р) K k(a

--^X cos h 2nnT(т - T) 1 X (2l + 1)---.

2п П=1             E         Vla + kXaT^

х

(8€ - 1)IV(ka)Kv(ka) + ka(l(,(ka)Kv(ka) + Iv(ka)K0(ka))              з

(8€ - 1)K2(ka)+2kaK0(ka)K_v(ka)                ^р р^

(1.17)

Используя (1.10) обозначим

∞∞

GMo(p. р) - - E(2l + 1) gM (р. р) =   Е(р + a)^-(1+1)(P + a)l =

4п                    4n

1=0

1=0

T

4п(р - р).

(1.18)

∞∞

GEo(p.Р) - E E(21 + 1) gli (р.р) = -4n                       8n

a21+1(1 - 8€)(р + a)

1-1(р + a)-1-1

1 = 0

1=0

(l - 4€ + 1)

.

(1.19)

Тогда.

GM (р,р) = GMo(Р,Р) + GMn(p,Р) =

T ²

4п²(р - р)^{2 +} 12

р       + о((р - р)=).

(1.20)

GE(т. р.т.р)

T∞

^GE0^(p. ^{р) +} GEn^(T. ^р.^т. ^р) = ~T~ E 8n

1=0

a²¹⁺¹(1 - 8€)(р + a)^-1-1 (р + a)^-1-1 (l - 4€ + 1)

T∞             ∞

^-2n X ^cos [^{2nnT(т - т)}] X ⁽²l⁺ 1)

n=1                    1=0

K ( k(a + р) IK ( k(a + р

V ^{(a + p)(a + p)}

х

(8€ - 1)IV(ka)Kv(ka) + ka(^I0(ka)Kv(ka) + Iv(ka)K0(ka) (8€ - 1)K2(ka) + 2kaK0(ka)Kv(ka)

Окончательно

G e (т, р, т,р) = GE (т,р,т,р) + GM (р,р).

(1.22)

Тогда, выражение ( 1.6 ) можно переписать в виде

G e (т,р; т, р)

1         T ²    T ⁴п²(р - р)²

4п²(р - р)^{2 +} 12 -     180

T ^у a²¹⁺¹(1 - 8€)(р + a) ¹ 1(р + a) ^{1 1}

8П1=           (i - 4€ + 1)

T∞

- — 'У cos |_2ппТ(т - T)J

х

х

∞

X(2l +1)

1 = 0

(8€ - 1)I_v(ka)K_v(ka) + ka^I_v(ka)K_v(ka) + I_v (ka)K_v(ka) (8€ - 1)K2(ka) + 2kaK0(ka)K_v(ka)

х

K^k(a + p)) K_v\k(a + p) уУ+УУ+У

+ O((p - p)3).

(1.23)

Отметим, что GM(p, p) совпадает с соответствующей функцией Грина пространства-времени Минковского.

2.    Перенормировка hф2i и анализ результата

В методе регуляризации раздвижкой точек процедура, перенормировки состоит в вычитании из G e (xⁱ,xⁱ) контр члена G ds [34] , который в пространстве (1.1) для х^г - xⁱ = 5^г_р (р - р) равен

GDS = 4п2(р - р)2 ’ и нахождению предела совпадающих точек. Все расходимости GE совпадают с расходимостями GM. Поэтому вводом

GM ren = lim (GM р ^ р

^- GDS ) .

(2.2)

Тогда в области р > 0

^a (^ф iren ^a GE ren ^a

т ² 48n²

∞

— У 16п2

1=0

( M lim GE ren ρ→ρ

(1 - 8€)

I aT

⁺ G^E) =

τ

(1 - 4€ + 1)(x +1)21+2   2п2(х +1)

+ lim GE = р М'

∞∞ xx (i+D х n=1 1=0

х

(8€ - 1)Iv (Tn)Kv (тп) + тЦ!^ (Tn)Kv (тп) + Iv (rn)K _v (тп) (8€ - 1)K2(тп) + 2тпК 0(тп)^(тп)

х

х [к!/^тп(х + 1))] , x = р/a,

т = 2nTa.

(2.3)

В продело р ^ то и 2) Tx + yoli-vy (ф iren - 12 + 4n (€ - 1/4) р2 .

(2.4)

При T = 0

^a (^ф iren

1 у ~  ^{(8€ - 1)!}v⁽y^)Kv⁽y^{) +} yh ⁰⁽y^)Kv⁽y^{) +} Iv⁽y^)K0(y))

2п2(Г+Х О dy 1=0 V----------------------------------------

[ Ку^у(1 + x)^ , x = р/a, У = ka, v = 1 + 1/2

(8€ - 1)K2(y) + 2yK0(y)Kv(y)

(2.5)

результат совпадает с результатом работы [35] . В силу симметрии результат справедлив и в области р < 0.

0.5

0.4- о.з-

0.2-

0.1-

0.5              1              1.5

|--Т= 0.01: -"Т= 5;-""С = 10|

а2<ф2>, ^=у

0.31

0.2- *

0.1-

0—---------------------,-----------,-----------,

0.5           1           1.5           2

х

^ттоЖ^ч^бГПННИ]

2   2

а <ф >,

5 = 0

Рис. 1. Графики функции ( 2.3) для £ = 1/5,1/8 и т = 2nTa = 0.01, 5,10 от x = p/a.

0.3

0.2

0.1

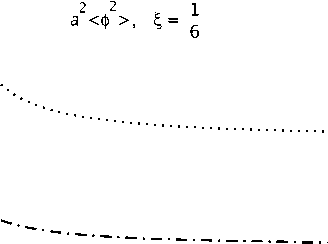
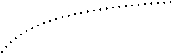
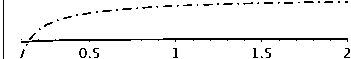
-0.1-

I---т = 0.0L -■ т = 5 •■■■т = 10

0.5         1         1.5         2

х

|--Т=0.01;-' Т= 5;“"Т = 10

Рис. 2. Графики функции (2.3) для £ = 1/6,0 и т = 2nTa = 0.01, 5,10 от x = p/a.

Заключение

Получено выражение и проведены численные расчеты квадрата, вакуумных флуктуаций h^2iren квантованного скалярного поля в пространстве-времени кротовой поры с бесконечно короткой горловиной в предположении о том, что поле является безмассовым, имеет произвольную связь со скалярной кривизной и находится в тепловом квантовом состоянии с произвольной температурой.

Работа выполнена в рамках реализации программы развития Научно-образовательного математического центра Приволжского федерального округа, соглашение № 075-02-2022-882