Поляризационные эффекты при отражении света от границы одноосного кристалла

Отражение электромагнитных волн от границы с анизотропной средой рассматривалось неоднократно (см. например [1]). Тем не менее детальные исследования поляризационных эффектов при отражении света от таких границ не проводились. Данная работа восполняет частично этот пробел. При отражении от границы двух изотропных сред поляризация волны никогда не сохраняется (за исключением двух тривиальных случаев s - или p -поляризованной падающей волны). Плоскость поляризации после отражения всегда прижимается ближе к границе раздела сред [2]. В случае анизотропных сред в отраженной волне всегда присутствуют обе s - и p -поляризации, что допускает возможность сохранения векторов Джонса при отражении. Чтобы определить, при каких условиях это выполняется, были получены и исследованы граничные условия для плоских электромагнитных волн в случае одноосного кристалла с осью, параллельной границе раздела кристалла и изотропной среды.

Граничные условия

Пусть электромагнитная волна падает под углом падения 6 на границу раздела изотропной среды и одноосного кристалла, как показано на рис. 1. На рис. 2 показаны направления волновых векторов в плоскости падения OXZ для волн в изотропной среде (обозначены как E) и для обыкновенной и необыкновенной волн в анизотропной среде (обозначены как D). Для волн, распространяющихся «сверху вниз», используется индекс «+», а для бегущих «снизу вверх» используется индекс «-».

Запишем проекции векторов напряженности электрического поля Е и напряженности магнитного Н на границу раздела в изотропной среде. Направления векторов для разных поляризаций выбираются так, как показано на рис. 3 и 4, таким образом, чтобы при нормальном падении направления напряженностей электрических полей в падающей и отраженной волнах совпадали.

Суммарные проекции полей записываются отдельно для каждой составляющей: для падаю-щей p -поляризованной волны (см. рис. 3) и s -поляризованной волны (см. рис. 4).

E px = cos 6 ( E P + EP )	H px = 0	Esx = 0	H„ = n cos 6 ( Es p - Es ) sx                s      s
E py = 0	H py = - n ( Ep- E p )	E sy = ( E s - E S )	H y = 0
E pz = sin 6 ( E p - E p )	H pz = о	E sz = 0	Hsz = n sin 6 ( E p P E s )

Мухин Ю.В., Гатауллина Ю.Р., Кундикова Н.Д.

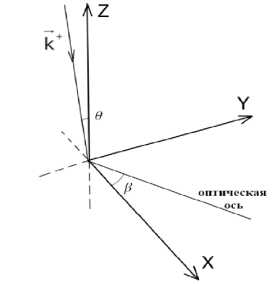
Рис. 1. Граница раздела OXY содержит оптическую ось кристалла, расположенную под углом β к оси OX

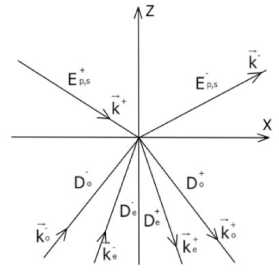
Рис. 2. Расположение направлений волновых векторов в плоскости падения OXZ

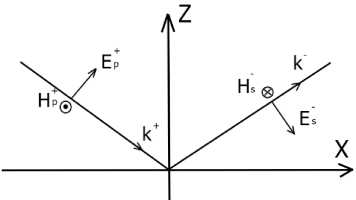
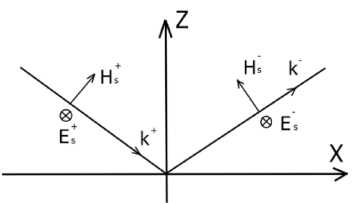
Рис. 3. Падающая p- поляризация                       Рис. 4. Падающая s- поляризация

Для записи проекций полей в одноосном кристалле удобно пользоваться индукцией электрического поля вместо напряженности. Это обусловлено поперечностью поля D по отношению к волновому вектору. Введём также обозначения углов, связанных с ориентацией полей и волновых векторов, упрощающие вид формул:

sin O e = n sin O / n e                 cos Y _e = cos в sin O _e               cos a _e = sin в sin O _e

sin Oo = n sin O / je!             cos Yo = cos в sin Oo              cos ao = sin в sin 0o имеют показатели преломления ne

e,   1 — n¹

e

—

sin² O cos² в

и n o = ^FI • Здесь n - по-

Перпендикулярные и параллельные оптической оси составляющие электрического E и магнитного H полей необыкновенной и обыкновенной волн выражаются тогда через индукцию электрического поля D следующим образом.

Для необыкновенной волны:

F - sin Ye ++           p   _ cos Ye ++ E e\\ =       D e            E e 1 =       D e e                    e i H eW = 0               „  _ D + H e 1 ne Для обыкновенной волны:	E e, = ^in ^ e D —         E e 1==^ D e 1                            b 1 H eW = 0              H _D; H e 1 ne
E oW = 0               F _D^ E o 1 e 1	EoW = 0                 F  _—o_ Eo 1 = e1
D +                  D + Ho\\ = sin Yo Y-         H o 1 = cos Yo Л- 4 e 1                   ^11	Ho\\ = sin Yo ro-       Ho 1 = cos Yo ro n e 1                  V e 1

Индексы «е» и «о» обозначают компоненты необыкновенной и обыкновенной волн, которые казатель преломления изотропной среды.

Граничные условия заключаются в непрерывности тангенциальных составляющих электрического и магнитного полей на границе раздела. Остается только «сшить» все полученные выражения в четыре граничных условия:

Для электрического поля, параллельного оптической оси:

cos в cos 9 ( E p + E - ) + sin в ( E S + E S ) = "'A' ( D e + D e ) S

Для магнитного поля, параллельного оптической оси:

- n sin в ( E p - E p ) + n cos в cos 9 (E S - E ) = snb( D_o " + D_o " )

Для электрического поля, перпендикулярного оптической оси:

- sin в cos 9 ( E p + E - ) + cos в ( E S + E ) = cos e s sin “ e ( D e + D — ) + c° ^ ( D p + D J )

Для магнитного поля, перпендикулярного оптической оси:

COSfZ n cos в(Ep - Ep) + n sin в cos 9(Ep - Es) =----e (Dp ne

- D e- ) - CC^ J ( D . _ D - )

Матрица отражения

Полученная выше алгебраическая система уравнений позволяет вычислить различные амплитудные коэффициенты отражения для разных поляризаций. В уравнениях (1)–(4) можно избавиться от компонент индукции электрического поля D и получить элементы матрицы отражения M , связывающей компоненты электрического поля в отраженной волне с компонентами электрического поля в падающей:

E

1 —

p

pp

sp

Ге⁺ )

Ep

— M

( e⁺P

Ep

к

e;)

rss   F+

ss A Es )

F+ к Es )

Здесь элементы матрицы отражения M даются выражениями:

rpp

E p    A i p C 2 - A 2 p C i

E p   B 2p C i - B i p C 2

, при E S = 0;

r sp

^E   B 2s C - B i s C 2

E S   A i s C 2 - A 2 s C i

при Ep— 0;

r ps

E S

F ⁺

Ep

A i p^B2 p   A 2 p^B1 p       77+ а

—-—-----—-, при E = 0;

B i p C 2 — B 2 p C i          ^s

r ss

es

es

B i s A 2 s — B 2 s A i s A i s C 2 — A 2 s C i

, при E p — 0.

Где введены следующие обозначения:

A i p , s = a 3p , s d i^e2 - ^aip , s d 3 ^e 2 ^- a 2 p , s d i^e3

A 2 p , s ^{— a} 4 p , s^d i ^e 2 ^{— a} i p , s d 4 ^e 2 ^{— a} 2 p , s^d i ^e 4

C i — C 3 d i e 2   c i d 3 e 2   c 2 d i e 3

B i p , s ^— b 3p , s d i ^e 2 ^- b i p , s d 3 ^e 2 ^- b 2 p , s d i ^e 3

B i p , s ^— b 3 p , s d i ^e 2 ^- b i p , s d 3 ^e 2 ^{- b} 2 p , s d i ^e 3

C 2 — c 4 d i e 2 — C i d 4 e 2 — C 2 d i e 4

a _i — cos 9 cos в ; a _{2 p} — - n sin в ; a _{2 s} — n sin в ; a ₃ — - a _i; a _{4 p} — — n cos в ; a _{4 s} — - a _{4 p} ;

bip   ai; bis        ; b2p   a2s; b2s     nai; b3p     ai; b3s        ; b4p nn к                • Q                    R               sin ye       sin Yo b4s — -nai; ci — sin в; c2 — -nai; c3 — cos в; c4 — nai; di —----- ; e2 — —-;=-

^1^±

7 sin a cos Yp     cos a 7   - cos a     sin a cos y d3 —----e-----; e —----J; d4 —------e; e4 —----J=—J .

Sv         SL        ne4F

В отсутствие поглощения и полного внутреннего отражения матрица M должна обладать определёнными свойствами. Во-первых, она должна быть вещественной матрицей. Помимо этого, по аналогии с линейными эрмитовыми операторами квантовой механики, она обязана быть симметричной. Симметричность M подтверждалась прямыми выкладками и вычислениями.

Мухин Ю.В., Гатауллина Ю.Р., Поляризационные эффекты при отражении света Кундикова Н.Д. от границы одноосного кристалла Эффект сохранения поляризации

В изотропных средах поляризация света никогда не сохраняется при отражении от их границ раздела. На границе с анизотропной средой ситуация совсем иная. Представим отраженную в изотропной среде волну в виде

f s-) p	=	r pp	Г 7 sp	( Е +1 E	= r	( Е +1 Ep	.                                        (5)
Е — V Es 7		г V rps	г ss 7	Е + V s 7		F + V ES 7

Алгебраическая система уравнений (5) может иметь нетривиальное решение только в случае равенства нулю детерминанта:

det

pp

— r

sp

= 0

ps

ss

—

Решение системы уравнений (5) и нахождение коэффициентов r аналогично решению задачи о расщеплении двукратно вырожденного уровня, разобранной в [3].

^r 1,2 = ^0,5 ( r pp + r ss ± w ) , w = J( r pp - r ss ) ² + ⁴ I r ps | 2

Выражения для векторов Джонса J падающей волны имеют при этом следующий вид:

J =

E +

Е +

Es 7

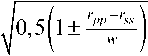
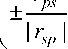
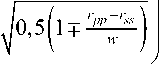
Наглядно представить поляризацию электрического поля удобно с помощью годографов нормированных векторов Джонса: точек или линий на поверхности сферы единичного радиуса в используемой системе координат. Волновые векторы при этом будут лежать в плоскости падения перпендикулярно векторам Джонса. В зависимости от угла падения 6 годограф вектора Джонса для одной из поляризаций прочерчивает на поверхности сферы линию от экватора (нормальное падение) и до полюса, где угол падения света 0 = 90°. Для различных положений оптической оси, разных углов β , получаются разные линии на сфере. На рис. 5 и 6 приведены годографы векторов Джонса J для сохраняющихся поляризаций: рис. 5 - для углов в < 45°, рис. 6 - для уг лов 45° < в < 90°.

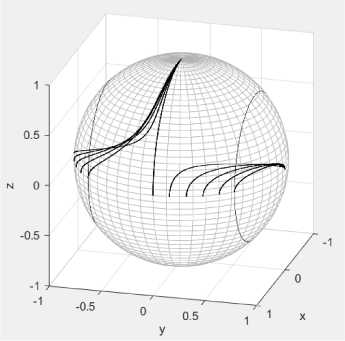
Рис. 5. Годографы вектора Джонса для углов β от 0° до 45° с шагом 9°. ^w = 1,7; Де^ = 1,55

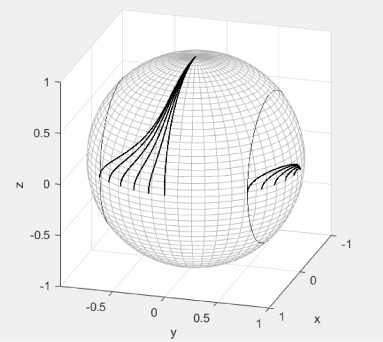
Рис. 6. Годографы вектора Джонса для углов β от 45° до 90° с шагом 9°. ^^ = 1,7; лДТ = 1,55

На рис. 6 видно, что для 45° < в < 90° плоскости сохраняющихся поляризаций могут принимать лишь ограниченные положения: ни одна из линий годографов на рис. 6 не пересекает вертикальные окружности на сфере, параллельные плоскости падения, в то время как для углов в < 45° каждая из линий пересекает эти окружности. Вертикальные окружности на рис. 5 и 6 соответствуют плоскостям поляризаций, составляющим угол в 45° с плоскостью падения. Данное свойство не зависит от оптических параметров кристалла, но может быть пояснено с помощью рис. 7, на котором показаны графики зависимости от угла падения 0 двух коэффициентов матрицы отражения при в = 10°.

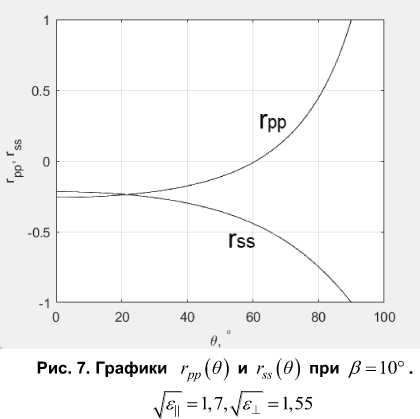
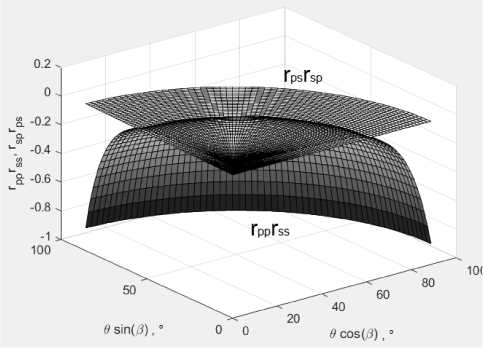
Рис. 8. График зависимости r _pp r _ss и r _ps r _sp в координатах O sin в и 0 cos в . ^ ^ = 1,7,^ Д 7 = 1,55

Кривые на графике имеют точку пересечения, которая присутствует для всех углов в <  45 ° • Это пересечение соответствует равенству модулей компонент векторов Джонса для сохраняющихся поляризаций, и значит, расположению плоскости поляризации под углом 45° к плоскости падения. Для углов 45 ° <  в <  90 ° такое пересечение кривых отсутствует, именно поэтому положение плоскостей сохраняющихся поляризаций в этом случае ограничено областями, показанными на рис. 6.

Угол Брюстера

Для границы двух изотропных сред угол Брюстера соответствует нулевому отражению p-поляризованного света. На границе с анизотропной средой p-поляризованный свет всегда будет давать s-поляризованную составляющую в отраженной волне. Поэтому сам термин и условия «Брюстера» следует относить здесь уже к другой поляризации, которая, очевидно, будет определяться углом в оптической оси к плоскости падения. Если условия Брюстера выполнены для одной поляризации, то ортогональная ей поляризация должна сохраняться.

Таким образом, условия Брюстера являются частным случаем сохраняющихся поляризаций с нулевым коэффициентом r в системе уравнений (5). Чтобы это было возможным, необходимо равенство нулю детерминанта матрицы отражения в (5): r pp r ss - r_psr_sp = 0.

На рис. 8 показаны зависимости rpprss и rpsrsp от угла падения 0 и угла в , взятых в поляр ных для этих переменных координатах: 0 sin в и 0 cos в . Пересечение двух поверхностей как раз и соответствует выполнению условий Брюстера. При выполнении условия вектор Джонса падающей волны приобретает вид

Г 1    )

— г 1г

^ ps / ss у

Условия Брюстера являются частным случаем сохранения поляризации при отражении. Другими словами, на линиях, изображенных на рис. 5 и 6, должны быть точки, соответствующие Брюстеровским поляризациям.

На рис. 9 показана макушка сферы единичного радиуса со следами годографов сохраняющихся векторов Джонса, на которых отмечены точки, соответствующие условиям Брюстера. Оказывается, что эти условия реализуются между углами Брюстера для

Мухин Ю.В., Гатауллина Ю.Р., Кундикова Н.Д.

коэффициентов преломления n e ( в = 0 ) =

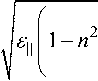
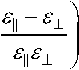
sin² О

и no = ^ Д Т • Брюстеровская

поляризация оказывается при этом близкой к p-поляризации с небольшой примесью s- поляризации на уровне нескольких процентов, но которая зависит уже от параметров кристалла.

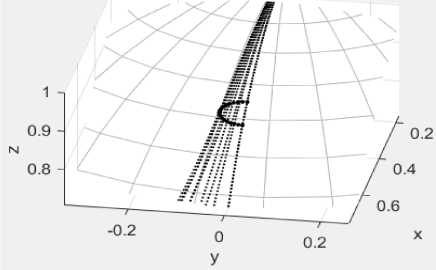
Рис. 9. Годограф векторов Джонса для углов Брюстера. Д= = 1,7, ^Js T = 1,55

Заключение

В настоящей работе были получены и исследованы граничные условия для плоских электромагнитных волн на границе раздела изотропной среды с одноосным кристаллом. Получены элементы матрицы отражения связывающей компоненты электрического поля в отраженной волне с компонентами электрического поля в падающей волне. Показана возможность сохранения поляризации при отражении от границы с анизотропной средой и получены условия для реализации этого эффекта. Исследована возможность существования эффекта Брюстера на границе с такой анизотропной средой. Брюстеровские поляризации оказываются близкими к p -поляризациям с небольшой примесью s -поляризаций.