Поляризационный тормозной эффект в импульсном лазерном поле

Тормозной эффект (ТЭ) в электромагнитном поле состоит в поглощении/вынужден-ном излучении фотона/фотонов электроном, рассеивающем на мишени (атоме/ионе). Это явление является фундаментальным излучательным процессом, который, в частности, используется для нагрева плазмы лазерным излучением. Существуют два механизма ТЭ (как и спонтанного тормозного излучения): обычный, когда фотон поглощается/излучается непосредственно рассеивающимся электроном, и поляризационный механизм, при котором взаимодействие с излучением осуществляется через электронный остов мишени, а энергия поля поглощается/излучается налетающим электроном.

ТЭ в монохроматическом поле изучался в ряде работ на протяжении последних нескольких десятков лет [1]. В связи с активным развитием технологии генерации лазерных импульсов с заданными параметрами [2] приобретает актуальность вопрос исследования ТЭ в импульсном электромагнитном поле.

Данная статья имеет целью обобщить описание поляризационного однофотонного ТЭ [3] на случай импульсного лазерного излучения.

Сечение (по отношению к потоку электронов) поляризационного однофотонного ТЭ при рассеянии квазиклассического электрона на многозарядном ионе заряда Z >>  1 с

• (с) Астапенко В. А., Кротов Ю. А., Сахпо С. В., 2025

@ Федеральное государственное автономное образовательное учреждение высшего образования

«Московский физико-технический институт (национальный исследовательский университет)», 2025

электронным остовом в монохроматическом поле с частотой ш и амплитудой Fo в кра-мерсовском пределе ш >>  “c_oui = mv³/Ze² (т, v - скороств и масса электрона) имеет вид [1]:

''  ■     ,'А ()2^^{,(ш)|2 F}2

где а(ш) - динамическая поляризуемоств мишени.

В дальнейшем рассмотрим резонансный случай, когда частота лазерного излучения близка к одной из собственных частот перехода в электронном остове иона ш ~ шо, шо - частота дипольно-разрешенного перехода в ионном остове. Тогда с учетом влияния лазерного поля на электронный переход в остове резонансная поляризуемость иона дается следующим выражением [4]:

«(ш, Ио) = ( ^ /о “ ^о — “ ⁺ i^y ,                      (2)

у 2тш /   (“о — ш)2 + у2 + Ио здесь /о - сила осциллятора перехода, у - константа затухания, Ио - резонансная частота

Раби, которая равна по определению

Ио = \ОЕ';

Выражение (1) справедливо в приближении точечного иона, когда можно пренебречь проникновением внешнего электрона в электронный остов. Мы также пренебрегаем возможным спин-орбитальным расщеплением Ар£ и доплеровским уширением Ад резонансного перехода, полагая, что частота Раби достаточно велика: Ио >>  A _Fs , A_d.

Подставляя резонансную поляризуемость (2) в сечение (1), получаем

^м =

4^F / Ze³ V 3^3 тиКш²

/о   “(шо — ш + iy )

2Z (шо — ш)² + у ² + Ио

Fo2.

Вероятность фотопроцесса за все время действия импульса лазерного излучения может быть представлена в виде [5, 6]:

W = Г Л^ш)^^doy J о         d“dS где

dN ph = с |F (ш,т )|² d“dS  4л²    Кш

• - число фотонов, составляющих лазерный импульс, в заданном частотном интервале d“, прошедших через элемент площади dS за все время действия импульса т, F(ш, т ) - фурье-образ напряженности электрического поля в импульсе.

В формулу (5) входит сечение фотопроцесса по отношению к потоку фотонов, которое связано с сечением по отношению к потоку электронов (1) следующим равенствами:

^^(ph)(“) = а^(е)(ш)    = а^(е)(ш) —^е^ 8лКш,                          (7)

JPh          сЕо гДе je,ph ~ плотность потока электронов и фотонов соответственно, Ne - концентрация электронов. С учетом (7) из (4) получаем

(p^{h) a} pol

(ш) =

X)

^3/2_Ne    ^е6/о²⁽“о ^{— ш)2} +у²

4 К с т² иш                   ²

(шо — ш)2 + у2 + И0j

Энергия, поглощенная в результате тормозного эффекта по поляризационному каналу, равна

∞

KE_p oi (г ) =

щУ72     ' S )^^{F (ш,г )|2 d}^-

(2^) 00

Равенство (9) следует из формул (5) - (6).

Выражение для энергии, поглощенной по обычному (статическому) каналу тормозного эффекта KE_ord, следует из (9) с заменой сечения поляризационного ТЭ на сечение статического ТЭ, которое в рассматриваемых приближениях равно [1]:

'           3 ( I'     - ^{Л 2}

•6

hcm2 vw3

(Ю)

Введем отношение, которое характеризует роль поляризационного канала и конечной длительности лазерного импульса в тормозном эффекте за все время действия импульса:

R(r, Ш с ) = ^Е^^^ ,                (Ц)

KEord(r ^от,шф где шс - несущая частота лазерного импульса. С учетом предыдущих формул отношение (11) равно

R(r, ш_с) =

/ m \²ш3^ |a(ш)|²ш|F(ш,г,Ш c )|²dш

Ze²)        00^ IF (w,r,w_c)|²dw

В резонансном случае равенство (12) с учетом выражения для поляризуемости (2) пе репишется в виде ш3 j ш-1----——ш) +1-----|f(ш,г,шс)|2dш

R(г,шc') =

/0 \2   о      [(шо -ш)2 +д2 + По]

2z)                 .0^ IF(ш,г,ш c )|²dш

В монохроматическом пределе г ^ от из (13) следует

R(r ^ от, ш_с) =

( Ш^У

(шо - Ш с )² +1²

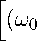
2 •

-Ш с )² +1² + Q2J

Применим полученные формулы для описания резонансного поляризационного тормозного эффекта при рассеянии квазиклассического электрона на литие-подобном ионе кислорода О⁵⁺, инициированного лазерным импульсом с длительностью г и несущей частотой, близкой к собственной частоте электронного перехода 2s ^ 3р в рассматриваемом ионе: Ш с х шо = 3.037 ат. ед. (86.2 эВ), /о = 0.26.

Отметим, что имеет место следующая связь между температурой плазмы и зарядовым числом наиболее представленного в плазме иона: Т = 0.025Z ². Исходя из этого равенства нетрудно убедиться, что при Z = 5 выполняется условие квазиклассичности движения электрона: р = Ze²/Hv = 4.47 > 1. Отношение частоты излучения к кулоновской частоте порядка 10, так что выполняется условие крамерсовского приближения. Таким образом, в рассматриваемом случае выполнены критерии приближений, для которых справедливо выражение для сечения ТЭ (1).

В атомных единицах для перехода 2s ^ 3р в ио не О5+ справедливо соотношение которое вытекает из определения частоты Раби (3). В дальнейшем рассматриваем достаточно сильное лазерное поле Fo > 0.01 ат. ед. Оценка показывает, что в этом случае можно пренебречь спин-орбитальным расщеплением Зр-уровня, поскольку для него △fs ~ 7 • 10-4 ат. ед. и соответственно Qo(F0 > 0.01 ат. ед.) >> Afs- Константу затухания у положим равной коэффициенту Эйнштейна Из^ для рассматриваемого перехода: 7 = ИзР25 « 10-6 ат. ед.

Рассчитаем по формуле (13) зависимость отношения R от несущей частоты, длительности и амплитуды лазерного импульса с гауссовской огибающей. Результаты расчета представлены на рис. 1-4.

На рисунках 1, 2 представлены зависимости R от несущей частоты для различных длительностей и амплитуд лазерного импульса, а также случай монохроматического лазерного поля (14). Видно, что для коротких импульсов отсутствует спектральный провал на собственной частоте резонансного перехода, который появляется с увеличением длительности, так что для т = 24 фс спектральная характеристика отношения (13) приближается к монохроматическому пределу (14). Из приведенных зависимостей следует, что в околоре-зонансной области частот вклад поляризационного канала в ТЭ доминирует над вкладом статического (R >>  1), за исключением узкого интервала вблизи собственной частоты перехода для длинных импульсов.

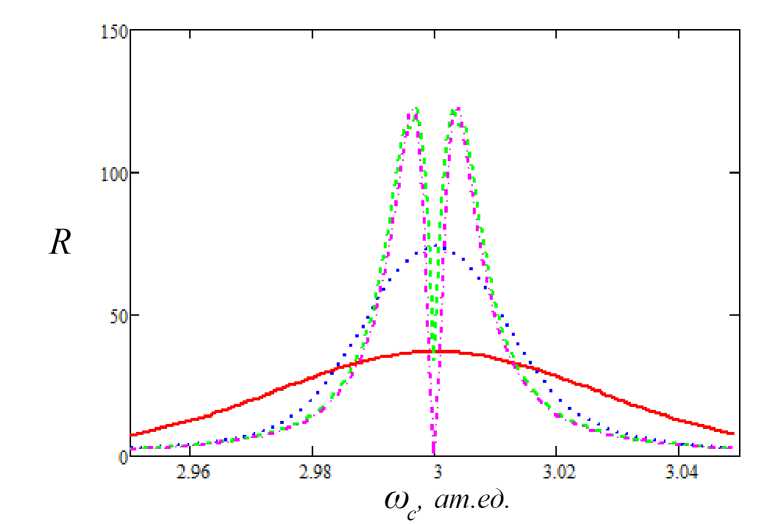
Рис. 1. Зависимость отношения R (формула (13)) от несущей частоты лазерного импульса для различных длительностей: сплошная кривая - т = 0.72 фс, пунктир - т = 2.4 фс, штриховая кривая - т = 24 фс, штрих-пунктир соответствует монохроматическому пределу (14); амплитуда напряженности электрического поля Fo = 0.05 ат. ед.

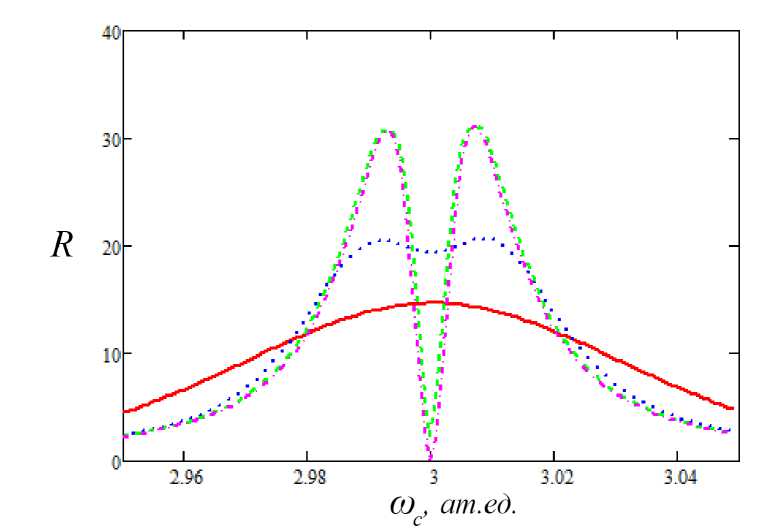
Рис. 2. То же, что на рис. 1, для F0 = 0.1 ат. ед.

Из сравнения рисунков 1 и 2 следует, что с ростом амплитуды лазерного импульса спектральный провал углубляется, а боковые максимумы раздвигаются. Последнее обстоятельство следует из вида резонансной поляризуемости в сильном поле (2).

На рисунках 3, 4 приведены зависимости отношения энергий R от длительности импульса для различных несущих частот и амплитуд импульса. Видно, что при относительно большой отстройке несущей частоты от собственной частоты резонансного перехода в этих зависимостях имеется максимум, который сдвигается в область меньших длительностей с ростом частотной отстройки. Кроме того, с ростом амплитуды лазерного импульса (рис. 4) максимум в зависимости R(r ) возникает и для резонансной несущей частоты ш_с = шо = 3 ат. ед., в то время как при ш_с = 3.02 ат. ед. максимум сглаживается.

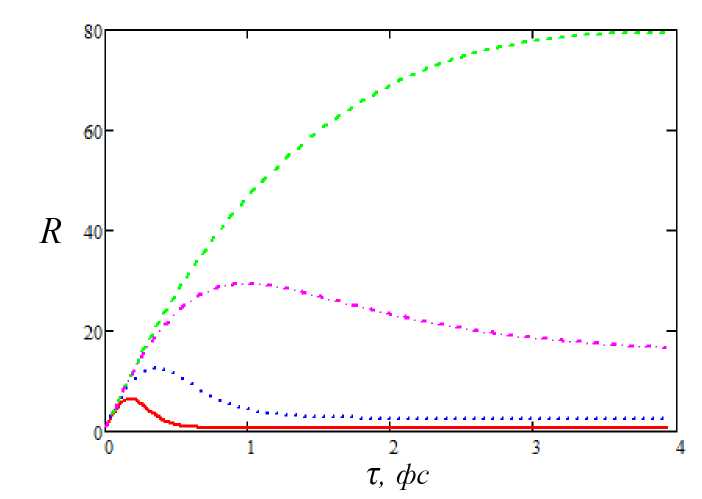
Рис. 3. Зависимость отношения R (формула (13)) от длительности лазерного импульса для различных несущих частот: сплошная кривая - ш_с = 2.9 ат. ед., пунктир - ш_с = 2.95 ат. ед., штриховая кривая - ш_с =шо = 3 ат. ед., штрих-пунктир - ш_с = 3.02 ат. ед.; амплитуда напряженности электрического поля F q = 0.05 ат. ед.

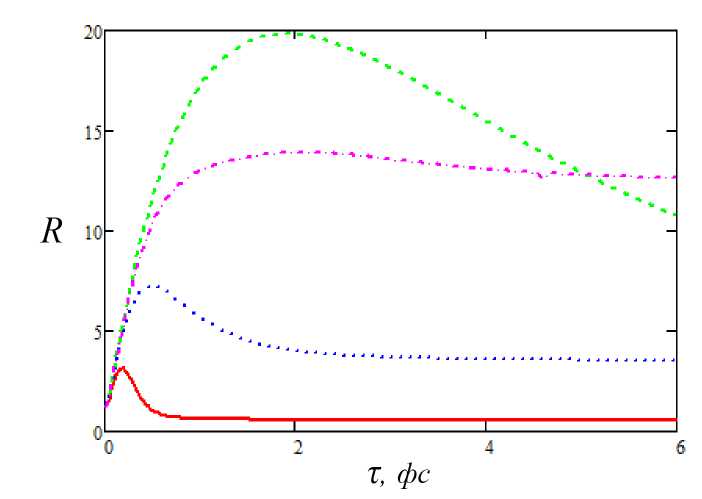
Рис. 4. То же, что на рис. 3, для F q = 0.1 ат. ед.

Таким образом, с помощью выведенных выражений, описывающих поляризационный тормозной эффект в поле лазерных импульсов, установлены его специфические черты, отличающие от аналогичного процесса в монохроматическом электромагнитном поле.