Полнофакторные модели точности выполняемых размеров многоинструментной обработки на станках-автоматах токарной группы

Введение . Основы теории проектирования и оптимизации многоинструментной обработки, базирующейся на учете силового взаимовлияния инструментов многоинструментной наладки, заложены в работе А.А. Кошина [1]. Однако им рассмотрены лишь два класса простейших плоских многоинструментных наладок, которые реализуются на станках-автоматах с кулачковым управлением.

Вопросы проектирования контурной траекторной обработки на станках с ЧПУ рассмотрены в работе В.И. Гузеева [2]. Однако они посвящены лишь одноинструментной обработке.

Н.Д. Юсубовым на базе проведенной классификации многоинструментных наладок современных токарных автоматов разработан комплекс матричных моделей точности выполняемых размеров, включающий модели искажения размеров и модели полей рассеяния размеров при обработке партии заготовок, где впервые учтена податливость технологической системы по всем координатным осям и допускается произвольное пространственное расположение инструментов наладки [2].

Модели погрешности обработки, сформированные в работах [2], учитывают лишь плоскопараллельные перемещения подсистем технологической системы вдоль координатных осей декартовой системы координат X , Y , Z . Такой подход к моделированию процесса образования погрешностей обработки допустим для деталей, имеющих габаритные размеры одного порядка по всем координатным направлениям.

Однако на практике нередки случаи, когда обрабатываются детали с габаритными размерами, существенно различающимися в разных направлениях. Например, длинные валы (преобладающий линейный размер), диски и фланцы (преобладающий диаметральный размер). В этих случаях существенный вклад в погрешность обработки могут вносить повороты обрабатываемой заготовки, особенно по направлениям преобладающих габаритных размеров.

На необходимость учета угловых перемещений заготовки под действием сил резания указывалось еще в работах А.П. Соколовского, В.С. Корсакова, Д.Д. Медведева и др. [3-23]. В них предложены даже простейшие аналитические зависимости для расчета этих угловых перемещений.

Однако все эти зависимости носят частный характер, включают в себя ряд параметров, определение которых на практике сопряжено с непреодолимыми трудностями. Например, центр поворота шпинделя вообще является виртуальным объектом, который невозможно практически замерить. Самое главное - эти модели не согласуются с общими законами механики упруго деформируемых систем. Поэтому они не могут быть использованы для построения единой теории точности обработки при учете возможных угловых перемещений подсистем технологической системы.

Полнофакторная модель искажения выполняемых размеров одноинструментной односуппортной обработки. Для описания перемещений тела в пространстве с учетом всех шести степеней свободы зададим его положение двумя параметрами (рис. 1):

• -    точка O ( x 0 ; y q ; z q ) , принадлежащая телу;

• -    вектор l единичной длины, принадлежащий телу и направленный, например, вдоль

преобладающего направления.

Все плоско-параллельные перемещения тела характеризуются перемещениями точки О . Угловые перемещения тела описываются поворотами вектора l вокруг точки О .

Перемещения тела происходят в результате воздействия силы F , приложенной в точке A ( x , y , z ), также принадлежащей телу.

Пусть вектор r = ( r_x , r_y , r_z ) - плоскопараллельное перемещение точки О . Вектор to = ( to _x , m _y , m _z )- угол поворота тела, а формально - вектора l , задающего ориентацию тела в пространстве, относительно точки О . Здесь r x , r y , r z - перемещения вдоль осей координат, to x , to _y , to _z - углы поворота вокруг соответствующих осей координат.

Тогда полное перемещение и точки A

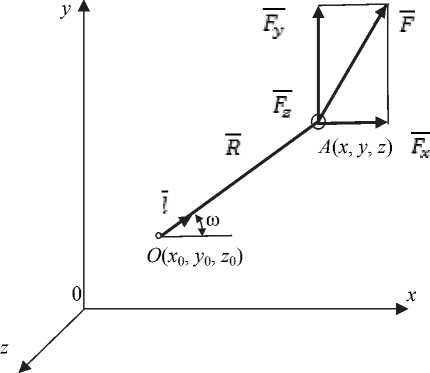
Рис. 1. Расчетная схема перемещений тела под действием приложенной силы при учете шести степеней свободы

складывается из плоско-параллельного и углового перемещений:

и = r + р, где второе слагаемое описывает именно угловые перемещения точки A p = toxR.

его

Вектор R задает ориентацию точки A (точки приложения силы F ) относительно точки O . Именно относительно этой точки и рассматриваются угловые перемещения точки A :

R = OA = { x - x q ; y - y q ; z - z q } .

Плоско-параллельное перемещение точки O под воздействием силы F с учетом податливости наложенных связей определятся, в соответствии с уравнениями, указанными в работе [1, 2], как:

r = eF.

Угловые перемещения точки A , обусловленные поворотом направляющего вектора l , определяются как векторное произведение ю х R . Если воспользоваться представлением вектора R

в виде матрицы a ₀ =

^{z — z} 0

^{— (} У ^— У 0 )

^{— ( z — z} 0 ) 0

—

x 0

—I

У ^— У о

■ ( x — x ₀) , то непосредственно выполнить векторное

0 ,

умножение юх R невозможно (умножение вектора на матрицу). Поэтому сначала определим противоположный вектор R хю (здесь умножается матрица а0 на вектор ю). С учетом матрицы имеем R хю = а06а0F . Поскольку справедливо соотношение: юх R = — R хю, выражение для угловых перемещений точки A примет вид:

Р = ^— a 0 ^ a 0 ^F .                                                                                ⁽⁵⁾

Для суммарного перемещения точки A (плоско-параллельное перемещение r базовой точки O и перемещение р вследствие поворота вокруг точки O) после различных преобразований получаем:

u = ( e — а 0 ^ а 0 ) F ,

где e - матрица координатной податливости e =

6 xx

вости 6=

^{6 yx} l^ zx

6 xy

⁶ УУ

6 yz

6 xz

^{6 yz}

6 zz J

.

exx

exy

exz

e yx

( e zx

e_yy e_yz ; 6 — матрица угловой податли-

eyz   ezz

Это уравнение описывает упругие перемещения тела от воздействия силы F при учете всего комплекса факторов, характеризующих податливость связей, фиксирующих положение тела в пространстве. Можно назвать это перемещение полнофакторным. Матрица e в этом уравнении характеризует податливость связей, ограничивающих плоско-параллельное перемещение тела. Тогда произведение трех матриц — а 0 6 а 0 можно трактовать как эффективную матрицу угловой податливости для точки A . Она характеризует податливость связей угловых перемещений точки A относительно точки O .

Поэтому полагаем, что уравнение (6) может быть положено в основу полнофакторной модели погрешности обработки. Для этого преобразуем сначала аналитические модели упругого контактного взаимодействия систем тел [1, 2] до уровня полнофакторных.

В модели контактного взаимодействия системы двух тел [1, 2], учитывающей только плоско-параллельные перемещения, при трансформации ее в полнофакторную модель, произведя ма- тематические выкладки, получим:

w = [ ( ^e 1 ^{— а}0 1 ⁶ 1 ^а0₁ ) + ( e 2 ^{— а}0₂ ⁶ 2 ^а0₂ ) ] P ,

где P - сила резания; e 1 и e 2 - матрицы координатной податливости соответственно тела 1 и тела 2 для плоско-параллельных перемещений; 6 1 и 6 ₂ - матрицы угловой податливости соответственно тел 1 и 2 для угловых перемещений; а ¹ _{0 1} и а₀ ² ₂ - матрицы, задающие координирующие векторы точки A приложения силы P для первого и второго тела соответственно;

O 1 ( x 0 , y 0 , z 0 ) и O 2 ( x 2 , y 2 , z 0 ) - базовые точки тел 1 и 2 (точки, относительно которых рассматриваются угловые перемещения остальных точек каждого тела).

Для плоско-параллельных перемещений вводилось понятие объединенной матрицы податливости e₁₂ = e 1 + e ₂ [5]. Из уравнения (7) видно, что для случая полного учета перемещений по всем шести направлениям степеней свободы общую объединенную матрицу податливости ввести невозможно, так как эффективные матрицы угловой податливости для заданных точек каждого тела представляют собой произведения из трех матриц. Поэтому можно использовать лишь уже введенную объединенную матрицу податливости для плоско-параллельных перемещений e ₁₂ , с учетом которой уравнение (7) преобразуется к виду:

w ^{= | e} 12 ^- ( a O 1 ^ 1 a O 1 ^{+ a}O₂ ^ 2 ^aO₂ ) ] P .                                                                 ⁽⁸⁾

Полнофакторная модель искажения выполняемых размеров многоинструментной двухсуппортной обработки. Рассматривая систему трех тел (применительно к двухсуппортным наладкам) с 6 степенями свободы для каждого тела и вводя характеристики податливости по каждой степени свободы, плоско-параллельная модель упругих перемещений [1, 2] трансформирована в полнофакторную:

w 1 ^=| e 01 — ( a \ ^ 1 a \ ⁺ a O ₀ ^ 0 a O ₀ ) ] P ^{1 + |} e 0 — ^aO ₀ ^ 0 ^aO ₀ J P ² ;                                      ⁽⁹⁾

w 2 ^=| e 02 ^- ( ^aO ₂ ^ 2 ^aO ₂ ^{+ a}O ₀ ^ 0 ^aO ₀ ) ] P ^{2 +|} e 0 ^{- a}O ₀ ^ 0 ^aO ₀ ] P ¹ .                                      ⁽¹⁰⁾

Здесь e0 и ^0 - матрицы плоско-параллельной и угловой податливостей тела 0 соответственно; e01 и e02 – суммарные матрицы плоско-параллельных податливостей контактирующих тел (под- системы 01 и 02); ^0, ^1 и ^2 - матрицы угловых податливостей контактирующих тел; P1 и P2 - векторы сил, приложенных соответственно к телам 1 и 2; a000 , a101 и a022 – матрицы, задающие координирующие векторы точки приложения сил P1 и P2 относительно базовых точек O0 , O1 и O2 , вокруг которых осуществляются угловые перемещения контактирующих тел. A1 и A2 – точки приложения сил P1 и P2 соответственно; w1 и w2 – искажения размеров с учетом как плоско-параллельных, так и угловых перемещений.

Полнофакторные модели полей рассеяния выполняемых размеров многоинструментной двухсуппортной обработки. По характеру силового взаимодействия Н.Д. Юсубовым выделены два предельных случая многоинструментных наладок [1, 2]: оппозитные (рис. 2) и сопозит-ные (рис. 3). В оппозитной наладке все составляющие сил резания одного суппорта направлены против соответствующих составляющих сил резания другого суппорта. Такие наладки традиционны для токарно-револьверных и токарных многошпиндельных автоматов с кулачковым управлением. В сопозитной наладке все соответствующие составляющие сил резания обоих суппортов направлены в одну и ту же сторону. На современных станках с ЧПУ токарной группы в равной мере используются оба вида наладок.

Основными факторами появления полей рассеяния выполняемых размеров в обоих случаях являются: колебания припуска, непостоянство механических свойств заготовок в пределах партии, разброс жесткости станков [1, 2]. Они предопределяют рассеяние определяющих факторов – координатных составляющих сил резания и податливости технологических подсистем (матриц податливости).

Механизм формирования поля рассеяния в двухсуппортной оппозитной наладке более сложен, нежели при односуппортной обработке. Разброс жесткостей технологической системы jF G jN

£ , £

и прочностных свойств материала заготовки C F е C n

v , v

опреде-

ляет масштаб интервала рассеяния искажений размеров w1 и w2 . Влияние же колебаний припус- ков tF G

A t    A t

^_7"; t + ~

на суппортах неоднозначно. Поскольку силы резания на про д ольном и

поперечном суппортах направлены друг против друга, колебания припуско в A t 1 и A 1 2 могут привести к изменению баланса сил. В результате этого и нтервалы рассеяния выполняемы х размеров имеют 3 варианта расположения [1, 2].

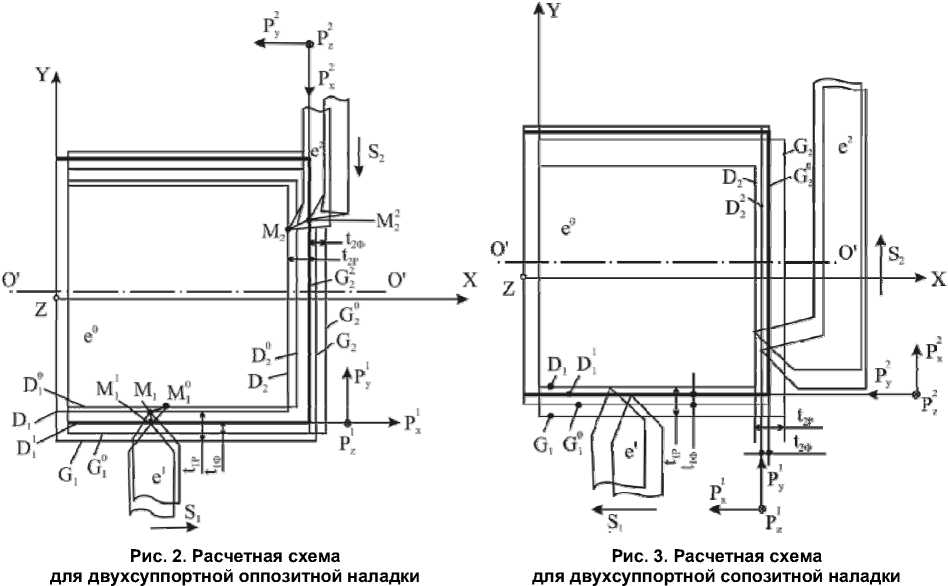
Вариант I характеризуется преобладающим влиянием продольного суппорта , т. е. перемещения от действия сил продольного суппорта настолько больше пер е мещений о т сил поперечного суппорта, что весь интервал рассеяния искажений расположен на положительной полуоси:

w max >  0; w min >  0 ^{. (11)}

Вариант II характеризуется преобладающим в л иянием поперечного суппорта , т. е. перемещения от действия сил поперечного суппорта настолько больше пере м ещений от сил продольного суппорта, что весь интервал рассеяния искажений располож е н на отрицательной полуоси:

w max <  0; w min <  0 ^{. (12)}

Вариант III характеризуется сбалансированностью влияния продольного и поперечного суппортов. Номинальное искажение выполняемого размера располагается в окрестности нуля, а интервал рассеяния искажений включает в себя начало координат:

w max >  0; w min <  0 ^{. (13)}

Ориентация поля рассеяния относительно номинала определяется с о отношени е м глубин резания на суппортах. Так, в варианте I припуск на продольном суппорт е максимальный, а на поперечном – минимальный. Максимум величины интервала рассеяния достигается при максимальной прочности материала заготовки и максимальной податливости технологической системы.

В итоге анализа всех вариантов расположения поля рассеяния сформи р ована еди н ая модель поля рассеяния размеров, выполняемых с продольн о го суппорта в двухсу п портной о п позитной наладке (см. рис. 2).

e 01 ti pt   e0t 2 pt + ^{( (} a O 1 ^ 1 a O 1 + a O ₀ ^ 0 ^aO ₀ ) t i p t ) + a O ₀ ^ 0 a O ₀ t 2 pt <

<_ ^e 01 ^A t i p A t ⁺ e 0 ^A t 2 p A t

^{+ ( -}

(арх ^i арх + ao ^o an )A t p\t an ^o an A to pM v O]^1 O1 O 0^0 O0 1 £^A t O0^0 O0 2 r A t

при ^to e 01 t i P t ¹ - e 0 t 2 p t + e 01 A t i P A 1 ⁺ e 0 A t 2 p A 1 +

+

^{+to (} a O 1 ^ 1 a O 1 ⁺ a o₀ ^ 0 ^aO ₀ ) t i ^pt ^{+ a}O₀ ^ 0 ^aO ₀ t 2 ^pt

;

+ (aOx ^1 aOx + aO0 ^0 aO0 )Ati pAt aO0 ^ 0 aO0 At2 pAt e01 t1 pt   e0 t2 pt + ( (aO1 ^1aO1 + aO0 ^0 aO0 )t1 pt ) + aO0 ^0 aO0 t2 pt < e01At1 pAt + e0A12 pAt   -(aox ^1aO1 + aO0 ^0 aO0)At1pat - aO0 ^0 aO0 At2 pat

A w 1 = <

to

1,^1     *11.         2

при I ^{1 +} I e 01 ^A t 1 p a t ⁺ e 0 ^A t 2 p A t ⁺

^{+ (1 +} 2)    ^{( a}O _x ^ 1 ^a O _x ^{+ a}O ₀ ^ 0 ^aO ₀ ^{) A} t i ^p A t   ^aO₀ ^ 0 ^aO ₀ ^A t 2 ^p A t

;

e ₀₁ A t 1 p A _t + e ₀ A 1 2 p A _t +   ⁽ a O_x ^ 1 ^aO_x ⁺ a O ₀ ^ 0 a O ₀ ^{) A} t 1 ^p A t   ^aO₀ ^ 0 ^aO ₀ ^A t 2 ^p A t <

< e 01 t 1 ^p_t    e 0 t 2 ^p _t + ^{( (} a O 1 ^ 1 a O 1 + a o₀ ^ 0 a o ₀ ) t 1 ^pt ) + a o₀ ^ 0 a o₀ t 2 ^p _t

12    1    2

при ^-to e 01 t 1 p t ^- e 0 t 2 p_t ⁺ e 01 ^A t 1 p A t ⁺ e 0 ^A t 2 p A t

— I

^to ( ^aO 1 ^ 1 ^aO 1 ⁺ a O₀ ^ 0 ^aO₀ )t i ^pt ^{+ a}O₀ ^ 0 ^aO₀ t 2 ^pt

^{+ (} a O _x ^ 1 a O _x ⁺ a o₀ ^ 0 a o₀ ^{) A} t i ^p A t

_

+

-

a O₀ ^ 0 a O ₀ ^A t 2 ^p A t .

Здесь введены вспомогательные векторы:

P t ¹ =

p A t =

^x p1^-1 У p1 z p1 C 1 t 1 ^Px S 1 ^Px V 1 ^Px

x x „1 -1 У „1 z „1 C1t1PyS1PyV1Py Py x p1-1 y p1 z p1

C 1 t 1 ^Pz S 1 ^Pz V 1 ^Pz P_z

- 1

;

y ₁ z ₁

CPx1S1Px V1Px yz 11

p t =

x_P 1 t 1 ^y C_P 1 S 1 ^y V 1 ^y

^X _P1 ^-1 У _P1 z _P1 x 1 t 1 ^Pz C 1 S 1 ^Pz V 1 ^Pz PP

;

xp 2 ^{- 1 y}p2 PyPy _{P y} t ₂ S ₂

x p2 ^{- 1} У „2 P_xP_x

2 t ₂ S ₂ x

C 2 t ₂ z

p A t =

X ₇ -1 У ₇

P ² S 2 Pz ²

z ₂

V2Py z2

V2Px z2

V ₂ ^Pz

.

xp 2 ^{- 1} y_p 2 z_p 2 x 2 C 2 t 2 ^Py S 2 ^Py V 2 ^Py PP

2 ^y 2 x ₂ C ₂ t ₂ ^x S ₂ ^x PP

^Pz ^{2 P}z ² x_{Pz 2} C_{Pz 2} t ₂ S ₂

z ₂

V2Px z V2Pz2

.

Вектор p_t характеризует степень влияния глубины резания t , вектор p _{A t} - степень влияния колебаний припуска A t , to = е + v - величины суммарного разброса свойств технологической системы. Величина силы резания как функции от параметра t определяется известной формулой p_t = c i t^x i s y v z i = x ; y ; z .

Аналогична модель поля рассеяния размеров, выполняемых в оппозитной наладке с поперечного суппорта:

A w 2 = •

2            i           2       2        0        0         2x 0       0 i e 02 t 2 pt e 0 t i pt + ( ( a O 2 ^ 2 a O 2 + a O 0 ^ 0 a O 0 ) t 2 pt ) + a O 0 ^ 0 aOt ti pt — ( an ^?an + an ^o an ) A t o p\an ^o an A t p\t — e02 2 p A t + e 0 ^ t i p A t + ( v O 2^ 2 O 2 O 0^0 O 07 2 lAt O 0^ 0 O 0 i 2A t ) 2 при to e 02 t i p t - e 0 t i p t + e 02 A t 2 p A t + e 0 A t i p A t + Г, 2,2.0, 0,.^. 0, 0.T T +to ( aO 2 ^ 2 aO 2 + aO 0 ^ 0 aO 0 ) t 2 pt + aO 0 ^ 0 aO 0 t i pt + + - ( aO 2 ^ 2 aO 2 + aO 0 ^ 0 aO 0 ) A t 2 p A t - aO 0 ^ 0 aO 0 A t i p A t ; 2122002001 e 02 t 2 pt   e 0 t i pt + ( ( aO 2 ^ 2 aO 2 + a O 0 ^ 0 a O 0 ) t 2 pt ) + aO 0 ^ 0 aO 0 t i pt — ( an ^9 an + an ^o an ) A t2 p\ao ^o ao A t i p\t e 022 p a t + e 0u t i p a t     v O 2^ 2 O 2 O 0^ 0 O 0 ' 2 ^A t O 0 ^0 O 0 i ^A t —                  + 2                                  2 (17) fl to 1 при 1 i + V 1 e 02 A t 2 p A t + e 0 A t i p A t + V 2 ;l                      j + (i + 1) - ( aO2 ^ 2 aO2 + aO0 ^ 0 aO 0 ) A t 2 p A t - aO 0 ^ 0 aO 0 A t i p A t ; e 02 a 1 2 p A t + e 0 a t i p A t   - ( aO 2 ^ 2 aO 2 + aO0 ^ 0 aO 0 ) A t 2 p A t - aO 0 ^ 0 aO 0 A t i p A t — _2 _ '                 2_               " — emt7 p 2 - ent i p f + ( - ( a 2 L2 a 2 + a 0 En a 0 ) t2 p 2 ) + a 0 En a 0 L p f 02 2 t 0 1 tO 22 O 2 O 00 O 02 tO 00 O 01 t 21     2   1 при -to e 02 t 2 pt - e 0 t i pt + e 02 A 1 2 p a t + e 0 A t i p a t - -to - ( aO2 ^ 2 aO2 + aO0 ^ 0 aO 0 ) t 2 p 2 + aO0 ^ 0 aO 0 t i p t + Г 2      2      0      0                 0       0           T + ( aO 2 ^ 2 aO 2 + aO 0 ^ 0 aO 0 ) A t 2 p A t aO0 ^ 0 aO 0 A t i p A t .

В сопозитной наладке (см. рис. 3) противодействия сил резания нет. Поэтому интервал рассеяния искажений имеет единственное положение – положительное. Максимум достигается при наибольших припусках на обоих суппортах, максимальной прочности заготовки и минимальной податливости технологической системы, минимум – в противоположной ситуации. В итоге, для полей рассеяния размеров, выполняемых в сопозитной наладке, получаем для продольного и по- перечного суппортов соответственно:

A w =to 6 oi t i p t + e 0 t 2 p t

+ e 0i ^A t i p A t + e 0 ^A t 2 p A t

+

+^{to - (} a O , ^ i a O , + aX ^ a O ₀ ) t i p t ■ + ^{- ( a}O , ^ 1 a O + ^aO₀ ² 0 a O₀ ^{) A} t i ^p A t

a X ^ 0 a X t 2 ^p 2

+

a O₀ ^ 0 a 00 ^A t 2 ^p A t ;

^A w 2 =^ e 02 t 2 p t + e 0 t i p + e 02 ^A t 2 p A t + e 0 ^A t i p A t +

^{+to (} a o 2 ^ 2 a o 2 + a o 0 ^ 0 ^aO ₀ ) t 2 ^pt ^aO₀ ^ 0 ^aO₀ t i p i

+

+

^{( a}0₂ ^ 2 ^a0₂ + aO₀ ^ 0 ^a O₀^{) A} t 2 p A t aO₀ ^ 0 a 00 ^A t i ^p A t

Подавляющее большинство реальных многоинструментных наладок не обладает такой однородностью в направленности сил резания [1, 2]. Поэтому для неоднородн ы х по направлению наладок нет единой схемы расчета полей рассеяния. С х ема расчета поля рассеяния определяется отдельно для каждого координатного направления, так как одна наладка в н аправлении одного выполняемого размера может быть оппозитной, а в направлении другого выполняемого размера – сопозитной. Если наладка в рассматриваемом направлении оппозитна, применяется модель (14), (17), но только ее часть в направлении рассматриваем о го размера; для сопозитной – модель (18), (19), также только ее часть в направлении рассматриваемого размера.

Итак, используя две специальные модели для одно р одных по направлениям наладок: (14), (17) для оппозитных и (18), (19) для сопозитных наладок и п ринцип систематики н еоднородных наладок по направлениям выполняемых размеров, можно расчетным путем определить величины полей рассеяния для всего класса двухсуппортных развернутых наладок.

Экспериментальное определение податливостей элементов технологической системы. Эксперимент предполагал измерение статической п о датливости. Для определения соответствующей податливости в направлениях x , y , z проводилось нагружение последовательн о й силой, после чего определялись перемещения в этих и других направлениях технологической системы (рис. 4). Нагружение и разгрузки элементов системы происходили постепен н о. Наличие стыков и трение элементов технологической системы вызывают несовпадение кри в ых нагрузки и разгрузки.

а) по оси Х подсистемы 0 от P y

б) по оси X подсистемы 1 от P x

Рис. 4. Фрагмент проведенного эксперимента по определению комплексной податливости подсистем 0 и 1

Замеры проводились на токарном станке INDEX V 160 с ЧПУ в Германии в Аахенской Высшей Технической Школе в лаборатории «Металлорежущие станки» на кафедре «Металлорежущие станки». Оборудование состоит из датчиков измерения силы (Kraftmessung – Kraft m essquarz Kistler Typ 9102 vorgespannt), усилителя нагружения (Ladungsverstaerker Kistler Typ 5004), измерения перемещений (Wegsensoren Solarton Typ AX / 1/SH), усилителя результатов измерения (Messverstaerker HBM Typ MGCplus, Empfindlichkeit 100 µ m / V oder 10 µ m / V ), сигналпринима-теля (Signalaufnahme (National Instruments High Speed USD Carrier Typ Ni USD 9162, National Instruments Messkarte Typ Ni 9215, Filter: KEMO Typ VBF 8; Lowpass 10 Hz DC) и персонального компьютера (Laptop HP Compaq nx 8220, Sofware: Ni LabView).

Полученные значения позволили охарактеризова т ь податливость технологической системы в соответствующих осевых направлениях (рис. 5). На рис. 5 даны уравнения регрессии и достоверности. Для определения угловой податливости на г ружение производилось момент о м сил, а угловые перемещения определялись по линейному перемещению двух точек в одной плоскости (см. рис. 4).

В табл. 1 показаны значения поворотного момен т а и углов поворота и последовательность определения угловых податливостей для подсистемы 0 и 1. Угол поворота θ подсистем определяется по формуле [7]

θ = arctg( d ₂ - d ₁)/ L ), (20) где d ₂ – упругое перемещение точки 1, мкм; d ₁ – упругое перемещение точки 2, мкм; L – расстояние между точками 1 и 2, мм.

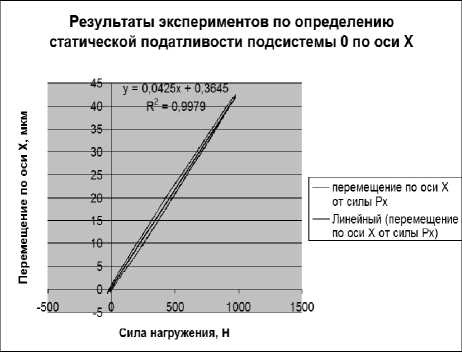
Рис. 5. Фрагменты результатов экспериментов по определению матрицы статической e податливости для плоско-параллельных перемещений подсистемы 0

Таблица 1

Момент M, N·m	Перемещение, mkm		Расстояние между точкой 1 и 2, mm	Угол, в р а дианах 10-3, rad	Угол , в градусах 10-3, град	Угловые податливости, 10-6 rad/N·m
	Точка 1	Точка 2
0	0	0	46,5	0	0	0
17,7	0,0131145	0,0084182	46,5	–0,100995699	–5,786627278	–5,70597E-06
35,4	0,0258645	0,0166082	46,5	–0,199060212	–11,40531004	–5,62317E-06
53,1	0,0386145	0,0247982	46,5	–0,297124722	–17,02399258	–5,59557E-06

Угловые податливости подсистемы 0

В табл. 2 и 3 приведена в качестве примера часть результатов экспериментов по определению комплексной податливости в соответствующих направлениях.

Таблица 2

Элементы матрицы статической e податливости для плоско-параллельных перемещений подсистемы 0 токарного станка INDEX V 160 с ЧПУ

Податливость	Значение, мкм/Н
ex 0 x – податливость в направлении оси Х от силы Px ;	0,0425
e x 0 y – податливость в направлении оси Х от силы Py ;	–0,0063
ex 0 z – податливость в направлении оси Х от силы Pz	–0,0047

Таблица 3

Элементы матрицы статической ξ угловой податливости подсистемы 1 токарного станка INDEX V 160 с ЧПУ

Податливость	Значение, рад/н ⋅ м
ξ 1 xx – податливость в направлении оси Х от силы Px ;	0,5 × 10 - 6
ξ 1 xy – податливость в направлении оси Х от силы Py ;	0,1 × 10 - 6
ξ 1 xz – податливость в направлении оси Х от силы Pz	0,5 × 10 - 6

Выводы

Предложены полнофакторные модели искажения и поля рассеяния выполняемых размеров многоинструментной обработки на станках-автоматах токарной группы, учитывающие податливость технологической системы по всем 6 степеням свободы и позволяющие тем самым учитывать угловые перемещения в технологической системе.

Разработана методология определения комплексной характеристики податливости технологической системы – матрицы координатных податливостей, характеризующие податливость подсистемы по координатным осям и их взаимовлияния и матрицы угловых податливостей, характеризующие сопротивляемость поворотам вокруг координатных осей и их взаимовлияния, и экспериментально определена комплексная характеристика податливости технологической системы – для каждой из подсистем комплекс из двух матриц.

На базе разработанных моделей имеется возможность выявлять степень влияния на точность обработки комплекса технологических факторов, включая структуру многоинструментной наладки, деформационные свойства подсистем технологической системы, режимы резания.

Разработанные модели позволяют прогнозировать точность обработки для заданных условий (структура наладки, свойства технологической системы, условия обработки), создавая методологическую базу САПР многоинструментной токарной обработки.