Полосно-пропускающие фильтры на плоско-поперечных сдвигах н-волноводов, выполненные по SIW-технологии

Современные микроэлектронные технологии позволяют создавать многослойные интегральные микросхемы с возможностью включения в их структуру трехмерных элементов, в частности прямоугольных волноводов и объемных резонаторов на их основе. Такая технология производства получила название SIW (Substrate Integrated Waveguide) – интегрированный в подложку волновод, который представляет собой волноводно подобную структуру, созданную двумя рядами металлических цилиндров, соединяющих две металлические пластины и ограничивающих диэлектрическую подложку. С помощью SIW-технологии непланарный волновод может быть изготовлен в планарной форме.

Преимущество SIW-технологии заключается в том, что она сохраняет все положительные качества классических волноводов: возможность передачи больших мощностей, малые потери, полностью экранированную структуру, высокую добротность резонаторов, – приобретая свойства микрополосковых структур: малые линейные размеры и вес, низкую стоимость и упрощенную технологию производства.

Важная особенность SIW-технологии состоит в том, что имеется возможность размещения всех элементов на одной диэлектрической подложке, включая пассивные компоненты, активные элементы и даже антенны. SIW-технология может быть успешно использована для создания таких устройств, как фильтры, направленные ответвители, фазовращатели, усилители, антенны и фазированные антенные решетки [1].

Фильтры, выполненные на классических волноводах, широко применяются в антенной технике и измерительном оборудовании. Одним из важных преимуществ фильтров, выполненных на волноводах, является минимальный уровень потерь, а следовательно, высокая добротность, особенно в сантиметровом и миллиметровом диапазоне длин волн [2; 3].

Хорошо известно, что применение волноводов сложного сечения позволяет существенно улучшить характеристики многих СВЧ-устройств. Например, по сравнению с прямоугольными волноводами П- и Н-волноводы обладают широкой полосой одномодового режима, а также меньшими массогабаритными характеристиками и малым волновым сопротивлением [4; 5].

Популярным подходом при построении волноводных полосно-пропускающих фильтров является применение плоско-поперечных неоднородностей в виде тонких диафрагм, стыков, сдвигов [6; 7]. Реализация фильтров на сдвигах волноводов в классическом исполнении, особенно на волноводах сложного сечения, трудно выполнима технологически, и поэтому она не имела широкого практического применения. В настоящее время с появлением SIW-техноло

гии и возможности интеграции в многослойные структуры волноводных элементов изготовление фильтров на плоско-поперечных сдвигах волноводов приобретает высокую актуальность.

Как показано в работе [1], существует возможность эффективно использовать при синтезе устройств, реализованных по SIW-технологии, в качестве начального приближения результаты синтеза для их цельнометаллических аналогов (устройств-прототипов). Таким образом, в данной работе осуществляется переход от классической структуры волноводного фильтра к фильтру, реализованному по SIW-технологии.

Процедуры анализа и синтеза полосно-про-пускающего фильтра на цельнометаллическом Н-волноводе реализованы с применением авторских алгоритмов [4–7], основанных на строгих электродинамических методах: методе частичных областей с учетом особенности электромагнитного поля на ребре, методе интегральных уравнений и вариационном методе.

1. Электродинамический анализ одиночных и связанных плоскопоперечных неоднородностей в гребневых волноводах

Рассматривается произвольная волна с порядковым номером p из спектра собственных волн волноводов сложного сечения с воздушным заполнением, падающая на плоско-поперечную неоднородность в положительном направлении оси z [4]. Потери энергии волн в металле не учитываем. Векторное электрическое поле в волноводе падающей на неоднородность волны имеет следующий вид:

^E pa ( x , y , z ) = Г e x E pX ( x , y ) + e y E pay ( x , y ) +

_Ia                                       (1)

+ e_zE_p^a_z ( x , y ) ] e - j ^Y zz^z .

Постоянная распространения p -волны в волноводе у pa будет действительной величиной для распространяющихся и мнимой для нераспростра-няющихся типов волн: у pa = - j у pa =

V ( k ² - k p )

у pa = k p - k ² , k — волновое число свободного пространства; k_p – критическое волновое число волны p . Временная зависимость выбрана в виде e j ^ш t ; b = I , II — номер волновода; a = h , e — индекс обозначающий принадлежность к классу Нили Е-волн соответственно. Полное электрическое поле в возбуждающем ( I ) и возбуждаемом ( II )

волноводах является суперпозицией электрического поля основной волны, электрических полей распространяющихся при данном значении рабочей частоты Н- и Е-волн и электрических полей не распространяющихся высших типов Н- и Е-волн, возбуждаемых вблизи неоднородности [6].

Коэффициенты отражения rqbpa и прохождения tqbpa всех волн находятся из условия равенства электрического поля EjI (x, y) = Ej11 (x,y) = Ejp (x,y) на апертуре неоднородности с учетом ортогональности собственных векторных функций вол- новодов:

1 + rpp = J E p(x, y) PpaE pa(x, y) ds, s rqp=j ep (x, y) p qa eqa (x, y) ds,                   (p)

s tqpa =j ep (x, y) p qIa e ^a (x, y) ds, s где Ejp(x,y) — неизвестное векторное электрическое поле на апертуре неоднородности s; pq — нормировочный множитель, определяемый из условия ортогональности собственных векторных функций. Интегрирование в выражениях (2) производится только по апертуре неоднородности s.

Используя условие непрерывности касатель- ных составляющих магнитного поля на отверстии неоднородности s, получаем интегральное уравнение, преобразуя которое [6], имеем в вариационной форме выражение для комплексной нормированной проводимости G + jB в месте неоднородности, учитывающее появление волн, распространяющихся и не распространяющихся в обе стороны от неоднородности:

G + jB =

MIh

IIa IIa         Ih Ih p pp 1 / in pn 1

n = 1

M IIh               M Ie    2

+Z’ nXIh + Z kiXk + n=1             k=1  Y k

M^IIe ,2            f      ®

₊ y ^w^ie₊ i- У у^Ihw^Ih-

+ / - He Wpk + j     /    Y n Wpn k=1 Yk            I n=MIh +1

да                               да p

- - Y i.IhWp? + - k^^wk + n=MIIh +1              k=MIe +1 Y k

^1 ■ IIe

да 2 ^k

— IIe Wpk k=MIIe +1 Y k

Ia Ia p pp ,

где ba Wpq

О pa

А2 = J E р (x, У ) 15ba (x, У ) ds V s ) f к 2 —:--. а = е. „ ba , с Y р /У ра, a = h. ba р q ,

рассеяния, которая может быть представлена в виде четырехклеточной матрицы, связь между элементами которой и коэффициентами отражения r_q^b_p^a и прохождения; t_q^b_p^a падающих на неоднородность волн определяется соотношениями, приведенными в [4].

Используя формулы для матриц рассеяния каждого из соединяемых многополюсников, по-

Комплексная проводимость G_p + jB p в месте неоднородности ( z = 0) нормирована на волновую проводимость падающей в I -м волноводе волны и представляет функционал, стационарный относительно малых вариаций векторного электрического поля E p ( x , у ) на апертуре неоднородности. Представленный функционал (3) не содержит ограничений ни на форму волновода, ни, что особенно важно, на форму апертуры неоднородности.

Представляя неизвестное векторное электрическое поле E_р ( x , у ) в отверстии неоднородности s в виде

N

E р ( x , У ) = ^ Uip Q i ( x , У ),                     (4)

i = 1

где U_ip – неизвестные коэффициенты разложения поля p -й волны; Q_i ( x , y ) – электрические собственные векторные ортонормированные функции, удовлетворяющие граничным условиям на контуре апертуры неоднородности, и решая методом Галеркина интегральное уравнение, получаем систему линейных неоднородных алгебраических уравнений относительно неизвестных коэффициентов разложения U_ip [4], знание которых позволяет вычислить электрическое поле (4) на апертуре неоднородности.

Зная E р ( x , у ), рассчитываем комплексную нормированную проводимость в месте плоско-поперечной неоднородности для каждой из падающих на неоднородность волн. Знание величины комплексной проводимости, рассчитанной для каждой из электромагнитных волн, падающих на неоднородность, позволяет проанализировать влияние плоско-поперечной неоднородности на характер прохождения волны в волноводном тракте.

Используя теорию цепей, можно представить плоско-поперечную неоднородность в волноводе сложного сечения в виде многополюсника с числом М входов и выходов, равным числу падающих на неоднородность волн в каждом волноводе. Такой многополюсник описывается нормированной обобщенной многоволновой матрицей лучаем матрицу рассеяния в случае каскадного соединения двух и более многополюсников.

Если плоско-поперечные неоднородности располагаются близко друг от друга и соединяются короткими отрезками волноводов, то взаимодействие соответствующих многополюсников происходит как по распространяющимся волнам, так и по высшим нераспространяющимся волнам.

Аналитические выражения для электромагнитных полей и критические волновые числа для волноводов со сложной формой поперечного сечения были получены на основе метода частичной области с учетом особенности поведения электромагнитного поля вблизи ребра [5].

• 2.    Синтез полосно-пропускающих фильтров на плоско-поперечных сдвигах

Процедура синтеза полосно-пропускающего фильтра осуществляется в два этапа. На первом этапе производится аппроксимация частотной характеристики фильтра с применением полиномов Чебышева; далее осуществляется расчет соответствующих проводимостей плоско-поперечных сдвигов для формирования резонаторов и четверть волновых связей с заданными параметрами, и наконец, определяются геометрические параметры волноводного фильтра. Этот этап можно назвать этапом радиотехнического синтеза.

Однако за счет того, что в волноводе существуют критический режим работы, многомодовый режим, взаимодействие неоднородностей по всему спектру волноводных мод в области ближнего поля, а также за счет того, что волновод – это линия передачи с дисперсией, эффективно использовать прототип фильтра на сосредоточенных элементах во всем рабочем диапазоне частот не удается. Таким образом, на втором этапе необходимо дополнительно применить алгоритмы прямого многопараметрического синтеза, взяв результаты первого этапа в качестве начального приближения.

В качестве базовой модели полосно-пропус-кающего фильтра выбираем модель каскадного соединения проходных резонаторов [2; 3], в которой каждый резонатор представлен отрезком регулярной линии передачи между двумя неоднородностями. Для аппроксимации АЧХ-фильтра будем использовать характеристику Чебышева.

Для фильтра нижних частот:

L ( Q ) = 10 lg[1 + h ² T ^C Q )], n = 1,2,3,..., (5) где T n ( x ) — полином Чебышева первого рода степени n .

Переход к другим значениям граничной частоты и другим видам фильтров, в частности к по-лосно-пропускающим фильтрам, производится с помощью замен частотной переменной Q :

1 I ГО ® 0 W I ГОо го

W = ®п 2 "^rom ,                             (6)

® 0

®0 = V ГОП1ГОП2, где W – относительная ширина полосы пропускания; Гоо — центральная частота; Гоп1, Гоп2 — нижняя и верхняя частоты среза ППФ.

Так как на СВЧ все элементы фильтров на сосредоточенных постоянных заменяются эле- ментами на распределенных постоянных, то основы синтеза фильтров с сосредоточенными постоянными легко могут быть распространены на фильтры с распределенными постоянными, если определять параметры звеньев фильтра через их добротности.

Выражение двусторонней нагруженной добротности i -го звена приводит к единому уравнению для последовательной и параллельной цепей.

Q i

g_i 2 W ^,

где g_i – единая переменная, имеющая смысл сопротивления элемента эквивалентной цепи фильтра низких частот.

Для Чебышевских фильтров с нечетным числом звеньев и заданным допуском на рассогласование в полосе пропускания |г| max нагруженные добротности рассчитаны и приведены в таблицах [3] с целью облегчения инженерных расчетов.

Вместе с тем [2] нагруженную добротность проходного резонатора, ограниченного, к примеру, такими плоско-поперечными неоднородностями, как сдвиги, можно выразить через параметры эквивалентной схемы (рис. 1)

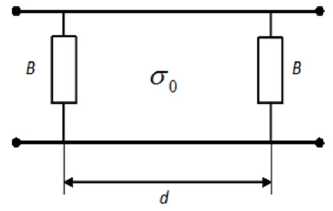
Рис. 1. Эквивалентная схема проходного резонатора

Q = B0L 1 + B O i ⁱ 2          4

Y o d i

^{1 -} ( ^ro kp / ^го 0 )

где B _{0 i} – реактивная часть проводимости i -го резонатора при их каскадном соединении и

Y o d = ГОо d / V f — электрическая длина резонатора на резонансной частоте.

Используя условие резонанса структуры, опи сываемой схемой на рис. 1,

B i (ГОо) = 2ctg Y oh ( ro o ) d i ,                             (9)

определяем

Y oh ( ro o ) d i = arctg — 2— + k п ,    k = 1,2,...    (10)

B i ^{( ro} 0 )

Таким образом, имеем два уравнения (8) и (9), при совместном решении которых и рассчитанных Qi можно определить реактивные проводимости B0i и длину проходных резонаторов на частоте Гоо .

В качестве длины резонатора часто используют значения электрической длины Y _oe (ГОо ) d i ~ п , т. е. d i ~ Ло / 2.

В результате

Q i

B O i   1 + B O i

arctg-- + к п

B i (гоо)

^{1 —} ( ^ro kp / ^ro 0 )

Так из решения этого трансцендентного урав- нения находятся B0i и из уравнения (11) – дли- ны резонаторов di =

,             arctg------ + к п

2      1 h >2 I         B i (ГОо)

^k 0 ^- ( ^koe )

длины соединительных отрезков между резонаторными звеньями:

d i ( i + 1) = (2 m - 1) Л ⁰- - k Л ⁰ + d i +^ ^{+ 1} .       (13)

На заключительном этапе осуществляется попытка найти размеры каждой i -й неоднородности, при которых мнимая часть ее шунтирующей проводимости на частоте Гоо была с определенной точностью равна B _{0 i} . Для сдвигов

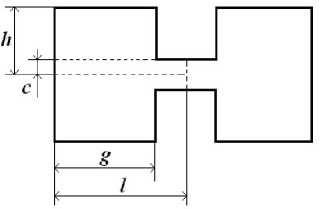
Рис. 2. Поперечное сечение Н-волновода

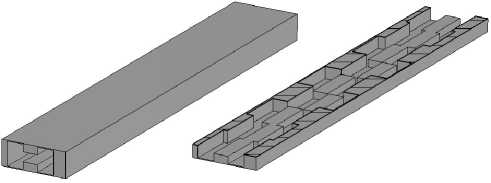
Рис. 4. Полосно-пропускающий фильтр на сдвигах Н-волно-водов в цельнометаллическом исполнении

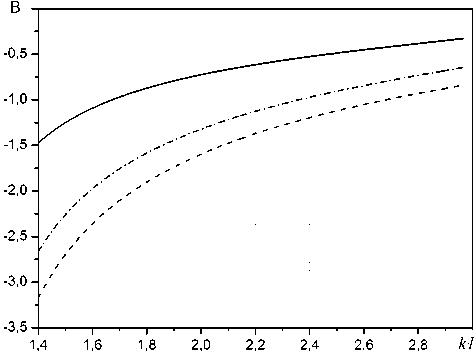
Рис. 3. Зависимость мнимой части проводимости В плоскопоперечного сдвига Н-волноводов от kl

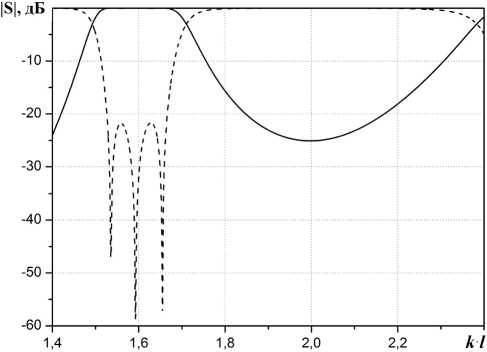
Рис. 5. Зависимость модулей S-параметров полосно-пропуска-ющего фильтра на сдвигах Н-волноводов в цельнометаллическом исполнении от kl

в волноводе сложного сечения приходится синтезировать размеры, используя зависимость В о i = В о i ( to o , L i ), где L i — вектор геометрических параметров i -й неоднородности.

• 3.    Результаты синтеза полосно-пропускающих фильтров

В качестве примера рассмотрим Н-волновод с размерами (рис. 2): g / 1 = 0.843, h / 1 = 0.25, c / 1 = 0.1. Для реализации процедуры синтеза фильтра проведем исследования проводимости В сдвига двух Н-волноводов вдоль горизонтальной оси. На рис. 3. представлена зависимость В от нормированного волнового числа kl для различной величины сдвига (сплошная линия — dx / 1 = 0.2; пунктирная линия — dx / 1 = 0.6; штрих-пунктирная — dx / 1 = 0.4). Из рис. 3. видно что проводимость В сдвига вдоль оси 0 х отрицательна, что говорит о ее индуктивном характере. С ростом kl проводимость плавно возрастает, а с увеличением значения dx / l – уменьшается.

По выше изложенной методике проведен синтез полосно-пропускающего фильтра на Н-вол-новоде.

На рис. 4 представлен внешний вид синтезированного полосно-пропускающего фильтра. Зависимость модулей S-параметров приведена на рис. 5 (S11 – пунктирная линия, S21 – сплош- ная линия). Геометрические размеры фильтра (длина резонатора – pi /l и величина сдвига – dxi /l) приведены в табл. 1.

Из графиков на рис. 5 видно, что полученный полосно-пропускающий фильтр обладает достаточно широкой полосой пропускания (10 ^), и широкой полосой запирания.

Для перевода полученной структуры фильтра в SIW-структуру необходимо заменить все вертикальные стенки волноводов решеткой металлических штырей, а также изменить заполнение с воздушного на диэлектрическое, введя соответствующие коэффициенты пересчета рабочей частоты [1]. При этом одной из основных характеристик, определяющей размеры поперечного сечения конечного устройства, является толщина диэлектрических слоев подложки в создаваемой многослойной интегральной микросхеме по технологии LTCC (Low Temperature Co-Fired Ceramic). В данном примере была использована подложка с толщиной 0.508 мм и диэлектрической проницаемостью б = 2.33. Для построения Н-вол-новода понадобится три диэлектрических слоя. При этом в зазоре между гребнями Н-волновода будет проходить один слой и по одному слою на толщину гребней. Диаметр металлических штырей выберем 0.16 мм, расстояние между штыря-

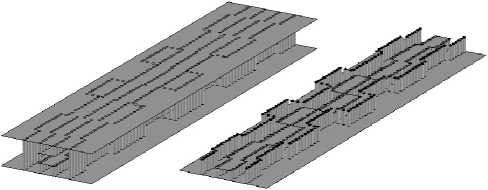
Рис. 6. Полосно-пропускающий фильтр на сдвигах Н-волно-водов в SIW-исполнении

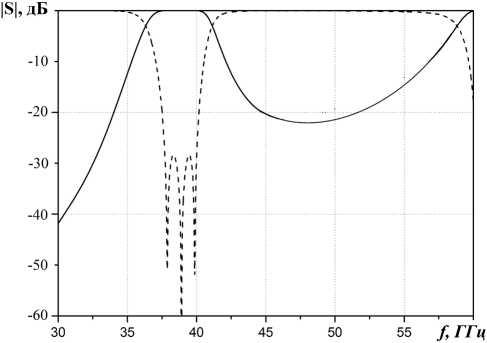
Рис. 7. Зависимость модулей S-параметров полосно-пропуска-ющего фильтра на сдвигах Н-волноводов в SIW-исполнении от частоты ми – 0.28 мм. Полученная структура фильтра, реализованного по SIW-технологии, представлена на рис. 6. Итоговые поперечные размеры Н-волновода составили – l = 3.6 мм, g = 2.802 мм, h = 1.524 мм, c = 0.508 мм.

Таблица 1

Размеры цельнометаллического фильтра

Для расчетов характеристик полученного SIW-фильтра было проведено компьютерное моделирование в пакете CST Microwave Studi o . Результаты компьютерного моделирования представлены на рис. 7 и практически полностью повторяют АЧХ цельнометаллического фильтра-прототипа (рис. 5). Необходимо отметить, что применение сеточных методов даже сегодня при наличии мощных ЭВМ является весьма трудоемким и длительным процессом и потому оправдано только на последнем этапе синтеза для проверки и более детального анализа получаемых результатов. Геометрические размеры фильтра приведены в табл. 2.

Таким образом, в данной работе решена задача электродинамического анализа и синтеза полосно-пропускающего фильтра на плоско-поперечных сдвигах Н-волновода в классическом цельнометаллическом исполнении и в виде SIW-структуры для интеграции в многослойные микросхемы. Полученные результаты подтверждают возможность применения при создании SIW-устройств в качестве начального приближения результатов синтеза их цельнометаллических аналогов.

Работа выполнена при поддержке Федерального государственного бюджетного учреждения «Российский фонд фундаментальных исследований». Грант «мол_а № 12-07-31003», руководитель Земляков В.В.

i	1	2	3	4
pi / l	0.483	0.497	0.485	0.529
dxi / l	0.043	0.033	0.126	0.050

Таблица 2

Размеры SIW-фильтра

i	1	2	3	4
pi , мм	2.572	2.936	2.554	2.752
dxi , мм	0.273	0.081	0.628	0.277