Полу эмпирические уравнения как способ отражения знаний при изучении физики

Согласно современным представлениям, любая наука становится серьезной лишь в том случае, если ее основные положения могут быть сформулированы на языке математики. Хорошо известно, что наиболее интенсивно математика используется в физике. Физика, как и другие естественные науки, наука экспериментальная, поэтому и математический аппарат используется в первую очередь для описания экспериментальных данных. Существенно, что некоторые возникающие при этом проблемы характерны не только для физики, но и для других наук. Предмет настоящей статьи - одна из такого рода проблем.

Для описания взаимосвязи между различными физическими свойствами используются формулы трех типов. Во-первых, это соотношения, получаемые на основе строгих физических теорий. Во-вторых, интерполяционные формулы, вид которых определяют, исходя из чисто математических соображений, например полиномом или рядом Фурье. Такого рода формулы используют в тех случаях, когда о природе явления, обусловливающего данную зависимость, нет никакой информации. Назначение формул - запись совокупности экспериментальных данных в компактной форме, т.е. замена таблиц. И наконец, в-тре-тьих, так называемые полуэмпирические формулы, имеющие промежуточный характер между первыми двумя. Формулы этого рода применяют в тех случаях, когда отсутствует строгая теория явления, как, например, в случае перехода кристалл-расплав. Формулы выбираются таким образом, чтобы при максимальной математической простоте по возможности точно описывать определенную совокупность экспериментальных данных. С другой сто роны, одну и ту же совокупность данных с учетом экспериментальных ошибок можно описать формулами различного вида. Поэтому вид полуэмпирической формулы определяют исходя из каких-либо теоретических соображений качественного характера. Проиллюстрируем такой подход на примере формулы для расчета энтропии однокомпонентного вещества в конденсированных состояниях.

Физикам хорошо известно полуэмпири-ческое уравнение Ван-дер-Ваальса для реальных газов. Это уравнение получено на основе уравнения Менделеева-Клапейрона, которое для модели идеального газа является строгим.

Существует, однако, и другое (менее известное) уравнение, являющееся для идеального газа столь же строгим, как и уравнение Менделеева-Клапейрона, - это уравнение Сакура-Тетроде:

На его основе было получено полуэм-пирическое соотношение для определения связи между энтропией и параметром беспорядка в конденсированных состояниях вещества следующим образом (см.: Ивлев В.И. К определению энтропии твердых тел и их расплавов // Журнал физической химии. 1987. Т. 61, №4. С. 1122).

Статистические теории агрегатных состояний базируются на функциях распределения, аргументом которых является энергия. Однако разность энергий не является главным различием между упорядоченным кристаллическим и сильно разупо-рядоченным жидким состояниями - изменение внутренней энергии при переходе от одного вещества к другому в одном и том же агрегатном состоянии или же в одном и том же веществе при изменении внешних факторов может быть одного порядка или даже превосходить изменение внутренней энергии при плавлении. Принципиальное различие между двумя конденсированными состояниями заключается в характере пространственного размещения атомов, точнее говоря, в степени разупорядоченности этого размещения. Отсюда следует, что при расчете термодинамических характеристик, например энтропии агрегатных состояний, энтропии плавления, имеет смысл искать пути, не связанные с введением в расчетные формулы энергии межатомного взаимодействия, а опирающиеся на пространственные, объемные соотношения.

Формально нетрудно перейти к функциям распределения, аргументом которых будет объем. В квазиклассическом случае статистический вес состояния определяется соотношением некоторый характеристический объем. В дальнейшем задача сводится к определению должным образом величин д$ и Э1и. Эти величины являются параметрами модели, которые сначала определим для случая, имеющего точное решение, т.е. для идеального газа, а затем проведем анализ возможности применения модели к одноатомному кристаллу.

Формулу (1) можно переписать в виде

S = N In

V

NVq

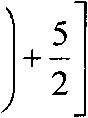
где VQ - так называемый квантовый объем,

7 V/2 2лй2

mkT ,

Вводя обозначение va е V/N и

ДГ = ^1. (2ЛЙ)5

где ApAq - фазовый объем; s - число степеней свободы.

Разделив числитель и знаменатель на Ар, получим

получим

S = Nln

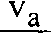
АР ^лй)⁵ / Aq

или в расчете на один атом

определив тем самым число состояний отношением двух величин, имеющих размерность объема в степени s/З. Энтропию системы тогда можно вычислить по формуле

8=1п(ДГ) = 1п(Л9/Эт)5/3,   (4)

в которой Д9 = ДхДуД/ , а

₉ <^2л^'

ДРхДРуЛР;

s = S/N = ln -^

С точки зрения термодинамики все агрегатные состояния равноправны, следовательно, наиболее общие формулы для расчета термодинамических функций вещества во всех агрегатных состояниях должны, в идеале, иметь одинаковую структуру. Тогда искомая нами формула для расчета энтропии конденсированных состояний вещества должна иметь под знаком логарифма, как и в выражении (9), отно-

^ЖЖШ^Я^Ш № 4,2000 шение объемов или величин, имеющих размерность объема.

Расчет по формуле (9) дает энтропию.

стремящеюся к бесконечности при стремлении температуры к нулю, что физически абсурдно. Чтобы устранить эту нефизичность. запишем формулу для расчета энтропии однокомпонентного веще- ства:

S = Nkln(l + va /vm).      (10)

Для полностью упорядоченного состояния вещества (идеальный кристалл при Т —> 0) энтропия, определенная формулой (10), в соответствии с требованиями статистической физики также стремится к

где т] - некоторый коэффициент, определя емый сортом вещества и типом его кри сталлической решетки.

Заменивв (9)г наv ,получим

S = In 1 + -* '

< Vm )

Для кристаллов в гармоническом приближении квадрат амплитуды тепловых колебаний пропорционален температуре:

2 2Т

Of = (TqT , где Оо - константа. В этом случае выражение (10) можно записать в виде нулю.

Расчеты показывают, что для газово- s = ln(l + ocTJ)

го состояния выполняется неравенство vAm » I, так что формулы (8) и (10) для этого состояния вещества дают практически одинаковые результаты. Следовательно, для наиболее разупорядоченного состояния вещества - газового - формула (10) с достаточно высокой точностью применима.

В газах атомами равномерно используется весь «предоставленный» им объем. В кристаллах же атомы (молекулы) большую часть времени проводят вблизи положений равновесия (узлов решетки), так что «эффективно используется» лишь часть объема, определяемая величиной амплитуды тепловых колебаний. В реальных кристаллах вплоть до температуры плавления относительная среднеквадратичная амплитуда тепловых колебаний о = Аг/г0

(г0 - минимальное межатомное расстояние, Дг-средняя амплитуда колебаний атома) имеет достаточно малые значения (о < 0,14-0,15), что позволяет определить «эффективно используемый объем» из соотношения при а = х0Оо-

При очень низких температурах для прироста энтропии твердого тела в модели Дебая справедливо соотношение

AS _ 4л4

Nk 50 q

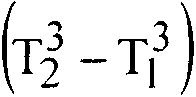
где ©d - температура Дебая.

Соотношение (12) в пределе % о-3 « 1 дает

Д5 = Хоао(т₂³-Т|³),       (15)

что совпадает с выражением (13), если положить

3   4л4

а = %о°о =—г 5®d

При высоких температурах выполняется условие аТ3 » 1

Тогда изменение температуры от Т( до Т, приведет к изменению функции s на величину v30=Tla3’         <П)

As = 31n —

Именно 1 акой характер температурной зависимости энтропии дает теория твердого тела в гармоническом высокотемпературном приближении.

Формула (12), имея достаточно простой вид, приводит к физически правильным результатам в трех предельных случаях: газ, кристалл при низких температурах. кристалл при высоких температурах.

Чтобы проверить применимость формулы (12) к кристаллам в области промежуточных температур, мы провели расчеты параметра 5 по уравнению (2) с использованием известных температурных зависимостей энтропии. При отсутствии таких данных энтропию рассчитывали по теплоемкости численным интегрированием, используя формулу

S = WdT       (|8)

О 1

Чтобы исключить подгоночный параметр /о. рассчитывалась величина а2 _Т0Г exp(S/R)-l ' а02 " Т [exp(S0/R)-l_ где а02 - значение параметра беспорядка при некоторой температуре То и соответствующем значении энтропии So. В расчетах было принято То = 300 К.

Расчеты были проведены для ряда металлов с кубическими кристаллическими решетками и некоторых ионных крисгаллов. Сравнение результатов наших расчетов с экспериментальными данными, а также с расчетными данными, полученными на основе различных теоретических моделей, говорит о том, что температурная зависимость параметра беспорядка и температурная зависимость согласуются достаточно хорошо.

Таким образом «сконструированная» нами формула (11), имея достаточно простой вид, приводит к физически правильным результатам и может быть использо- вана для описания как газового, так и конденсированного состояний.

ПРИМЕНЕНИЕ СОВРЕМЕННЫХ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ ДЛЯ ИССЛЕДОВАНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ СЕЛЬСКОХОЗЯЙ СТВЕНКОГО ПРОИЗВОДСТВА

ТА.Певцова, доцент кафедры ИВТ МГУ им. Н.П.Огарева

Появление персонального компьютера в 80-90 гг. стало грандиозным достижением научно-технического прогресса, который вызвал к жизни новые науки и новые информационные технологии. В настоящее время во всех развитых странах современные информационные технологии (СИТ) прочно внедряются в различные сферы человеческой деятельности: промышленность, сельское хозяйство, производство, экономику, торговлю, культуру, науку, образование, учебный процесс и т.д. Современные информационные технологии в основ ном применяются для выполнения трудоемких математических расчетов, для обработки, хранения и передачи больших объемов информации по каналам телефонной. кабельной и спутниковой связи, для работы в информационной сети Интернет и глобальной информационной сети WWW.

Переход экономики к рыночным отношениям и проводимые в стране и регионах реформы актуализировали многие экономические проблемы как в промышленности, так и в сельском хозяйстве. Важнейшими проблемами в сельском хозяйстве являют-