Полуаналитический метод решения уравнений газовой динамики в переменных Эйлера

В работе [1] описан метод решения системы уравнений механики сплошной среды, записанной в лагранжевых переменных, который отличается от традиционных методов тем, что конечными разностями заменяются только производные по пространственным переменным. В результате такого подхода уравнения в частных производных сводятся к системе обыкновенных дифференциальных уравнений на пространственной сетке. Для малого временного интервала было найдено приближенное аналитическое решение этой системы уравнений. Полученное аналитическое решение дает возможность описать динамику рассматриваемой системы во всем требуемом временном интервале. Применение данного метода для решения задач газовой динамики и расчета упругопластических течений в твердых телах показало, что данный метод обеспечивает высокую точность выполнения законов сохранения и характеризуется высокой устойчивостью решения, что обусловлено отказом от аппроксимации конечными разностями производных по времени.

Поскольку применение лагранжевых переменных для решения задач газовой динамики ограничено характером течений рассматриваемой системы, то возникает необходимость обобщения метода [1] на случай решения задач в эйлеровых переменных. В данной работе приводится описание применения метода [1] к решению задач газовой динамики в эйлеровых переменных, тестирование его на стандартных задачах путем сравнения результатов расчета предлагаемым методом с решениями, полученными базовым методом крупных частиц (МКЧ) [2], различные модификации которого широко используется для решения многих прикладных задач [3, 4].

Описание метода для эйлеровых координат

Рассмотрим систему уравнений газовой динамики в эйлеровых координатах в одномерном случае (законы сохранения массы, импульса и энергии):

8р ^ = о д t     д x

д(pv)  д(Pv2) __дР д t       дx       дx

d( pU) + d( PUv) = _p dv

S t        d x         S x

Здесь и далее p - плотность, v - массовая скорость, U - внутренняя энергия единицы массы,

P – давление. Данную систему уравнений следует дополнить начальными и граничными усло- виями.

Чтобы данная система уравнений обеспечивала выполнение второго закона термодинамики, в ней применяется неравновесное давление, которое учитывает конечное время релаксации физической системы к равновесию [5]. Следствием конечного времени релаксации к равновесному состоянию является то, что при уменьшении объема газа с конечной скоростью он в каждый момент времени не находится в равновесии, и тогда неравновесное давление может быть представлено в виде

P = р 0 + S P , (4) где P ⁰ - равновесное давление, которое находится через уравнение состояния P ⁰ = P⁰ ( p , U ) , S P = c² Sp - неравновесная добавка, обусловленная локальным изменением массовой плотности среды при сжатии, c - скорость звука. Локальное изменение плотности определяется как Sp = рт _ге1 , где T rel = § / c - время релаксации к равновесию, ^ - характерный линейный размер рассматриваемого объема среды. Поскольку изменение плотности среды связано с изменением объема соотношением p / p = - V / V , то из сказанного выше следует, что при сжатии среды неравновесная добавка к давлению имеет вид при V <  0:

S P = -p c ^ V / V . (5)

Адиабатическое расширение среды происходит за счет убыли внутренней энергии, причем максимальная скорость убыли внутренней энергии определяется свойствами самой среды и реализуется при равновесном процессе. Примером может служить разлет газа в пустоту [5], который является равновесным процессом (энтропия сохраняется). Таким образом, в случае расширения среды, когда V >  0, величина S P = 0 .

Для численного решения уравнений (1)–(3) на занятую область наносится неподвижная сетка x 1 , x ₂,.. . x i ,.. .x₇ . Массовая скорость среды v_t определена в узлах, а центрах ячеек определяются термодинамические характеристики среды p i _{+ 1 / 2}, m i _{+ 1} / ₂, P i _{+ 1} / ₂, U i _{+ 1} / ₂.

Для построения численной схемы проинтегрируем уравнения (1) и (3) в интервале от xi до xi+1, а уравнение движения (2) - в интервале от xi-1/2 до xi+1/2. Для малых интервалов интегри- рования можно записать соотношения:

^x i + 1

m i + 1/2 = j p ^dx = p i + 1/2 £+1/2 , ( ^mU ) i + 1/2

xi

x + 1

x i + 1/2

= j p U dx , ( mv ). = j p v dx ,

xi

^x i - 1/2

где i i _{+ 1/2} = x i _{+ 1} - x i есть объем ячейки с единичной поперечной площадью.

Сумма диагональных элементов тензора скоростей деформации определяет скорость относительного изменения объема и, соответственно, массовой плотности при сжатии или разрежении. В плоской геометрии разностный аналог этого выражения будет иметь вид:

^(V v ) i + 1/2 =f

d v )     _ v + 1 ^{- v} i _ V + 1/2

.

^{d x} ) i + 1/2     i^i + 1/2      ^i + 1/2

Таким образом, имеем Vi+1/2 = vi+1 -vi. Данное выражение характеризует изменение объема массы в ячейке только за счет процессов разрежения или сжатия без потоков массы через границы ячейки.

В результате интегрирования уравнения (1) получим:

^d m i + 1/2 S t

^-( J i + 1 ^- J i ) ,

где потоки массы через границы ячеек вычисляются как в [2]:

\pi-1/2,  vi> 0  _           F Pi+1/2,  vi+1

Ji = Vpl            ^J Ji+1 = Vi+1|

Lpi+1/2,  vi < 0              lpi+3/2,  vi+1

mi .-.,  1 ""aTvi = -( Pi+1/2 - Pi-1/2 )-(Ii+1/2 - Ii-1/2

где потоки импульса через границы x i _{- 1/2} и x i _{+ 1/2} вычисляются аналогично потокам массы:

I i - 1/2

= ^V i - 1/2

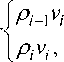
^V i - 1/2 >  ⁰

^V i - 1/2 <  ⁰

г                  J pivi, i+1/2 = Vi+1/2 1

L ^p i + 1 ^V i + 1 ,

^V i + 1/2 >  ⁰

^V i + 1/2 <  ⁰

v i ± 1/2 = ^0,5 ( ^V i ± 1 ^{+ V} i ) , P i = m i ⁴¹/^{2 +} m i ^1/2 , ^m i = ^0,5 ( ^m i + 1/2 ^{+ m} i - 1/2 ) . x i + 1 ^- x i - 1

Результат интегрирования уравнения (3) может быть представлен в виде

^d( mU ) i +1/2 _ p i                                                z.x

-----7-----= -Pi+1/2 (vi+1 - vi) - (^i+1 - +),                            (8) ot где потоки внутренней энергии вычисляются аналогично потокам массы или импульса:

~      \ ^p i - 1/2 ^U i - 1/2 ,   ^V i >  ⁰ ~           / ^p i + 1/2 ^U i + 1/2 , ^V i + 1 >  ⁰

^ = Vi * 1                         , ^7+1 = V/                                .

l ^p i + 1/2 U I + 1/2 ,   ^V i <  ⁰              l ^p i + 3/2 U I + 3/2 ,   ^V i + 1 <  ⁰

Уравнения (6)–(8) представляют собой систему обыкновенных дифференциальных уравнений на всей пространственной сетке. Будем интегрировать эту систему на некотором временном интервале от t n до t n _{+ 1}.

Полагая, что в интервале tn < t < tn+1 потоки массы через границы ячеек постоянны, решение уравнения (6) и новая плотность запишется в виде mi+1/2 (tn+1 ) = mi+1/2 (tn ) + (Ji-+1 - Ji ) At, pi+1/2 (tn+1 ) = mi+1/2 (tn+1)/6i+1/2*            (9)

Чтобы получить систему дифференциальных уравнений для скорости, продифференцируем уравнение (7) по времени, полагая, что потоки массы, импульса и неравновесная добавка (5) по- стоянны в рассматриваемом временном интервале, то есть

^ = 0, d l i + iZ! = 0, d ^ P i + L/l = 0.

S t ²           S t             S t

Выразим также частную производную от давления по времени через субстанциональную производную:

d P i °1/2 d t

= P i + 1/2

/ 5 P ⁰ )

v ------        .

I   ⁵ x J i + 1/2

Полную производную по времени в (10) представим в виде

P i + 1/2 = ( C ² p )._+1/2 =-0 + 1/2 ( V + 1 - V i ),                            (11)

где Q i _{+ 1/2} = p i _{+ 1/2} с 2 н _1/2/ ^ i _{+ 1/2} , ^ i _{+ 1/2} - эффективный объем ячейки, который учитывает, что при ее сжатии возмущается лишь слой. Таким образом, следуя [1], эффективный объем ячейки будет определяться выражением

6 + 1/2 =

с A t , V i + 1 - V i <  0

6 + 1/2 , ^V i + 1 ^{- V} i ^ ⁰"

С учетом сделанных замечаний и выражений (10) и (11) получим d2 V;   _   9v-

—+ 2y —i- + ^2 V = L, at2        dt где

1 dm    2    1 z                x         1 Fz                       z / 8P)/

Yi =--57, t»i =—< Qi+1/2 + Qi-1/2 ), Li =— (Qi+1/2 Vi+1 + Q-1/2 Vi-1 ) + l V^- I     -l V^- I mi dt        mi                         miL                          V  dx /i+1/2  I  dx)j-1/2 J

Для построения разностной схемы для вычисления входящих в последнее выражение производных удобно представить vdP/дх = d(vP)/дх — Pdv/дх. Тогда имеем dP

v— I  =—— dx Ji+1/2   2^i+1/2

[ vi + 1 ^{( P} i + 3/2    ^P i + 1/2 ) ^{+ v} i ( ^P i + 1/2

—

dP I               1 Г / T->         71                /7-7

^— P i — 3/2 ) ] •

v— I     =—---- L ^v i ⁽ P i + 1/2 ^{— P} i — 1/2 ^{) + v} i — 1 ^{( P} i — 1/2

.  ^d x J i — 1/2    2 5 — 1/2

Здесь также уместно привести разностную аппроксимацию для вычисления неравновесной добавки к давлению:

5 P i + 1/2 =

^{— (} c P ) i + 1/2 ⁽ v i + 1 ^— v i ) ’   v i + 1 ^— v i < ⁰

.

0,                       Vt _{+ 1} ^— v i > 0

Таким образом, выражение (12) представляет собой систему дифференциальных уравнений, решение которой позволит найти поле скоростей во всех узлах эйлеровой сетки. Для решения (12) необходимо задать начальные условия: vi (tn) = vin и (dvi / dt)n , которое находится из уравнения (7), где все величины в момент времени t должны быть известны. Подставляя (6) в (7), можно записать второе начальное условие в виде где

n d v i |

dt J

--77+{^{( P} i + 1/2 ^{— P} i — 1/2 ^{) + (} ^ i + 1/2 m i ( t v )

—

¥ i — 1/2 ) }   ,

I 0, ¥ i + 1/2 = ]      z

[ P i + 1 ^{( v} i + 1

—

v i + 1/2 >  ⁰

x                 _n, i—1—1/2 = vi)vi+1/2, vi+1/2 < 0

P i — 1 ⁽ v i — 1 ^— v ) v i — 1/2 , v i — 1/2

0,

v i — 1/2

> 0

.

< 0

Для малого временного шага можно получить простое аналитическое решение системы (12).

Полагая в (12) найденные для момента tn величины yi, Ю2, Li постоянными на шаге интегрирования, можно решение (12) записать в виде где

v i ( t n + 1 ) = v n ⁺

1 — e ^—

';At C (QAt) + у S^QAtl

,

Q2 = ю2 — z 2, Q = ^021, C (QAt ) =

cos ( QA t ) ,   Q ² >  0

V          ,    ,  S(QAt) = ch (QAt), Q2 < 0

sin ( QA t ) , Q ² >  0

sh ( QA t ) ,   Q ² <  0

.

Для решения уравнения (8) воспользуемся методом разделения по физическим процессам, для чего представим искомое решение в виде где 3Uf+1/2

—

U + 1/2 ( t ) = C i + 1/2 + - 1/2 + Cm, приращение внутренней энергии за счёт работы сил давления, 8 U^< O + 1V’ ₂

- прираще-

ние внутренней энергии за счёт конвекции.

Уравнение для 3CP + 1/2 запишем в виде ^д е ттР   _

^{3 U} i + 1/2 = ^— d t

m i + 1/2

^P i + 1/2 V + 1/2 ,

Отметим, что в уравнении (15) не учитываются потоки массы и энергии, что соответствует описанию в переменных Лагранжа. Подставляя выражение (14) в уравнение (8) и учитывая (15), запишем уравнение для 3Ci°01v/v2 в виде д (m UConvA

V              ) i + 1/2

S t

^—(^ i + 1

—

n

U i + 1/2 *

Уравнение (16) записано в переменных Эйлера.

Начальные условия для уравнений (15), (16) имеют вид 5 C P.1/2 ( t n ) = З и^ ^ ( t n ) = 0.

Интегрируя по времени выражение (11) от t_n до t < t_n^_x и учитывая (4), запишем выражение

P i + 1/2 ( t ) - P + 1/2 ( t n ) + 5 P i + i/2- Q i + i/2 ( V ( t ) - V ( t n ) ) i _{+ 1/} 2

Подставляя (17) в (15), получим после интегрирования выражение

.

SUi+m - n    ■ mi+1/2 L

- P (tn )AV + Q ^

!++

где ^AV i + 1/2 = V + 1/2 ^A .

Интегрирование уравнения (16) с учетом (6) приводит к выражению

A t n

5 U i + 1/2 ^- _n+1 { L ^P i + 3/2 ⁽ U i + 3/2 - U i + 1/2 ) v i + 1 J_{v <0}-L ^P i - 1/2 ^{( U} i - 1/2 ^- U i + 1/2 ) v i J„ _>0 } . ⁽¹⁹⁾ m i + 1/2 ¹ v ^{+ 1} vi ’

Таким образом, здесь приведен полный набор формул для описания динамики газа или жидкости в одномерной геометрии. Выражения (9) с приведенными в (6) потоками позволяют определить массы и плотности вещества в ячейках в новый момент времени. Выражение (13) позволяет вычислить новое поле скоростей, а выражения (14), (17) и (18) – внутренние энергии в ячейках. Новые равновесные давления и температура находятся с помощью уравнения состояния.

Основным приближением, которое было сделано при интегрировании системы (1)–(3), является постоянство Q _/+1/2 на шаге интегрирования A t . Это приближение выполняется, если на шаге интегрирования относительное изменение объема мало, то есть

A t

v i + 1 ^- v i ^ i + 1/2

< ^ H ,

где £н - некоторая малая величина. Данное условие позволяет найти величину шага интегриро- вания рассматриваемой системы. В случае состояний среды, близких к покою, или в случае глад- ких течений сформулированный выше критерий для выбора временного шага работать не будет. Поэтому для выбора временного шага при интегрировании уравнений применяется комплексный критерий, включая условие Куранта:

A t - min

^ H ^ i + 1/2 X v i + 1 ^- v i l

£ c ^

c

,

где £ _C ~ 1/3 - характерная константа в условии Куранта, £ _H ~0,01. Условие (20) проверяется для всех ячеек. Обычно оба условия дают близкие значения временных шагов, однако в области распространения ударных волн первое условие будет определяющим.

Точность интегрирования рассматриваемой системы можно повысить, решение (13) осуществить в два этапа. На первом этапе по формуле (13) для момента времени t_{n + 1/2} - t_n + A t /2 находится поле скоростей v i^{n + 1/2}, L n ^{+ 1/2}, а также потоки массы и энергии через границы ячеек. На втором этапе по формуле (13), в которой вместо L n подставлено L n ^+1/2 , находим v in . По формулам (9) и (18) вычисляются новая масса, плотность и внутренняя энергия через потоки для мо^мента t n + 1/2 .

Тестовые расчеты

Для верификации полуаналитического метода в эйлеровых координатах были решены одномерные задачи о распаде произвольного разрыва, о распространении стационарных ударных волн различной интенсивности и проведено сравнение полученного решения с аналитическим и решением, полученным базовым методом крупных частиц.

Задача 1. Распад произвольного разрыва. В некоторой области, ограниченной отрезком [0;1] (см), находится газ, в начальный момент времени ( t - 0 ) разделенный контактной границей на две подобласти. Показатель адиабаты у - 5/3. Геометрия сетки: N - 800 равномерно распределенных точек вдоль оси x .

Начальные распределения параметров газа вдоль пространственной координаты x равны

Р 1 = 3,87 кг/м³; T₁ = 611,5 К; U₁ = 0 м/с; Р₁ = 1,4 - 10 6 Па; x < 0,5 см;

р ₀ = 2,58 кг/м³; T 0 = 91,7 К; U ₀ = 0 м/с; P 0 = 1,4 - 10 5 Па; x > 0,5 см.

На рис. 1 представлены распределения параметров на момент времени t = 4,5 мкс. Решение, полученное полуаналитическим методом (ПА метод), совпадает с аналитическим решением [6], что говорит о высокой точности метода. Исходя из графиков, видно, что в момент времени, отличный от нуля, влево начинает распространяется волна разрежения, вправо - ударная волна. Решение, полученное численными методами, имеет «размытие» в области контактного разрыва. Решение, полученное базовым МКЧ, дает небольшой скачок параметров на фронте ударной вол- ны.

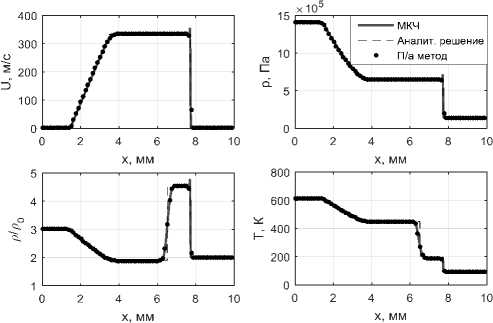
Рис. 1. Распад произвольного разрыва. Распределения скорости, давления, безразмерной плотности и температуры на момент времени t = 4,5 мкс

Задача 2. Распространение сильной ударной волны (УВ). В некоторой области, ограниченной отрезком [0;1] (см), находится газ (показатель адиабаты у = 5/3), начальные значения параметров которого равны:

р ₀ = 1,29 кг/м³, T 0 = 300 К, U 0 = 0 м/c, P 0 = 2,29 - 10⁵ Па; 0 < x <  1 см .

Через границу ( x = 0 ) в расчетную область втекает стационарный поток с параметрами:

P = 10 P o , U i , T , р.

Параметры U_x , T , p рассчитываются из соотношений на разрыве (соотношения Ренкина-Гюгонио). Геометрия сетки: N = 800 равномерно распределенных точек вдоль оси x .

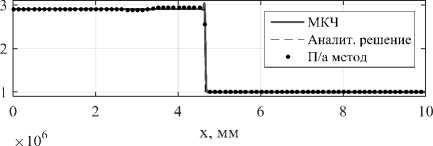
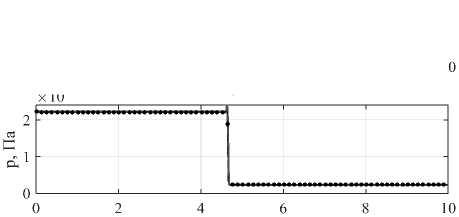
На рис. 2 представлены распределения параметров падающей сильной ударной волны на момент времени t = 3 с. На рис. 3 представлены распределения параметров отраженной ударной волны на момент времени t = 9 с. Полуаналитический метод дает хорошее совпадение с точным решением как для падающей, так и для отраженной ударных волн, в отличие от МКЧ. Решение, полученное базовым методом крупных частиц, имеет сильные осцилляции при отражении ударной волны от жесткой стенки. Это говорит о том, что МКЧ нуждается в введении дополнительных слагаемых, обеспечивающих устойчивость решения, не всегда имеющих физическую обоснованность. Одним из способов обеспечения устойчивости решения МКЧ является введение искусственной вязкости [7], в которую входят эмпирические константы. Использование таких слагаемых делает метод не универсальным. В то же время полуаналитический метод не требует введения никаких искусственных добавок.

Задача 3. Распространение слабой УВ. В некоторой области, ограниченной отрезком [0;1] (см), находится газ (показатель адиабаты у = 5/3), начальные значения параметров которого равны:

р ₀ = 1,29 кг/м³, T 0 = 300 К, U ₀ = 0 м/с, P 0 = 2,29 - 10⁵ Па; 0 < x < 1 см .

Через границу ( x = 0 ) в расчетную область втекает стационарный поток с параметрами

P = 1,5 P 0 , U 1 , T , р.

Параметры U ₁, T₁, p рассчитываются из соотношений на разрыве. Геометрия сетки: N = 800 равномерно распределенных точек вдоль оси x .

X, мм

Рис. 2. Распространение сильной ударной волны. Распределения безразмерной плотности и давления на момент времени t = 3 мкс

X, мм

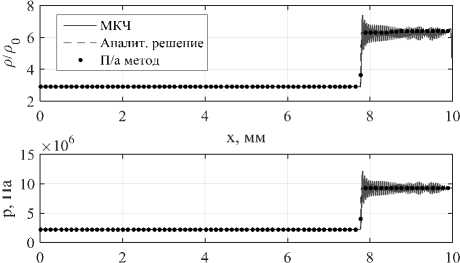
Рис. 3. Распространение сильной ударной волны. Распределения безразмерной плотности и давления на момент времени t = 9 мкс

На рис. 4 представлены распределения параметров падающей ударной волны на момент времени t = 6 мкс. На рис. 5 представлены распределения параметров отраженной ударной волны на момент времени t = 24 мкс.

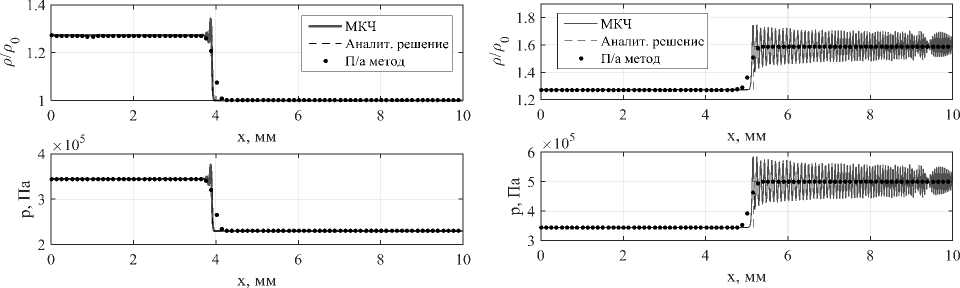
Рис. 4. Распространение слабой УВ. Распределения          Рис. 5. Распространение слабой УВ. Распреде- безразмерной плотности                            ления безразмерной плотности и давления на момент времени t = 6 мкс                и давления на момент времени t = 24 мкс

Исходя из полученных графиков для слабой ударной волны, видно, что решение, полученное базовым методом крупных частиц, не совпадает с аналитикой и показывает сильные осцилляции, то есть метод не устойчив при описании распространения слабых ударный волн. В свою очередь решение, полученное рассматриваемым методом, полностью совпадает с аналитическим, что говорит об универсальной применяемости данного метода для решения различных прикладных задач.

Заключение

В данной работе представлен полуаналитический метод в эйлеровых координатах для решения задач гидрогазодинамики. Представлены результаты верификации данного метода на одномерных задачах и сравнение с другим численным методом. Предложенный в данной работе метод показывает высокую точность для ударных волн различной интенсивности, что делает метод универсальным и применяемым для различных прикладных задач.

Данный метод применим для расчетов в многомерном случае, поскольку в этом случае описанный здесь алгоритм решения задачи сохраняется полностью.