Получение корректной информации о механическом состоянии глазного яблока на основе показаний анализатора реакции глаза (ORA)

RUSSIAN JOURNAL OF BIOMECHANICS

В анализаторе реакции глаза ( ORA ), используемом для измерения внутриглазного давления и оценки вязкоупругих свойств роговицы, последняя подвергается быстрому нестационарному воздействию узкой осесимметричной струи сжатого воздуха. Выдаваемая ORA информация основывается на статистическом сопоставлении получаемых данных с результатами измерений внутриглазного давления аппланационным тонометром Гольдмана без анализа реализуемых в устройстве физических процессов. Для такого анализа нами была разработана математическая модель, в которой роговица рассматривается как вязкоупругое тело Фойгта, а склеральная область как нульмерный объект, упруго откликающийся на изменения внутриглазного давления. Настоящая работа посвящена дальнейшему развитию этого подхода, концентрируясь на учете конкретных особенностей работы прибора при оценке реальных механических характеристик глазного яблока по предоставляемым ORA показателям. Установлено соответствие между давлением в камере, использованным при тарировке прибора, и действующим на роговицу давлением. Показано, что для глаза с нормальными упругими характеристиками методика, реализуемая ORA , дает величину внутриглазного давления, совпадающую с показанием тонометра Гольдмана, если параметр вязкоупругости роговицы (время релаксации ее деформаций) не слишком велик. Для больших значений этого параметра предложен алгоритм уточненного расчета внутриглазного давления. Расчеты показывают, что поправки, вносимые учетом влияния индивидуальных значений механических характеристик глазного яблока на внутриглазное давление, хотя и приводят к некоторому уточнению, сопоставимы с ошибками самого процесса измерения, дающего лишь грубую оценку этой величины. То, для чего прибор незаменим, – возможность определения параметра вязкоупругости роговицы, для расчета которого предложены два алгоритма. Этот параметр зависит только от механических свойств роговицы, что отличает его от традиционно используемого для оценки ее вязкоупругих свойств непосредственно определяемого ORA корнеального гистерезиса, который зависит также и от давления. Можно ожидать, что параметр вязкоупругости, имеющий отчетливый физический смысл, окажется эффективным и для диагностики.

Введение                                         применяемых в клинике для оценки механического со стояния глаза [1]. В этом устройстве глаз подвергается

Анализатор реакции глаза (ORA), разработан-    быстрому (несколько десятков миллисекунд) воздей- ный фирмой Reichert, – один из популярных приборов,    ствию узкой осесимметричной струи сжатого воздуха

Эта статья доступна в соответствии с условиями лицензии Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0)

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0)

переменного давления с фиксированием таких параметров нагружения, при которых центральный участок роговицы приобретает форму, близкую к плоской. В отличие от обычного пневмотонометра, в котором отслеживается момент уплощения, достигаемый в процессе повышения давления в струе, а последующее прекращение воздействия не контролируется, в ORA поддерживается контролируемое падение давления с фиксацией момента второго уплощения. Получаемая информация используется как для оценки внутриглазного давления, так и для вычисления некоторых дополнительных показателей.

Непосредственно ORA не измеряет ни внутриглазное давление, ни какие-либо физически определенные характеристики механических свойств глазной оболочки. Физическая интерпретация выдаваемых прибором параметров основывается на статистической обработке результатов и их сопоставлении с данными как измерений внутриглазного давления аппланационным тонометром Гольдмана [1–3], так и эмпирических исследований механических и структурных свойств глазной оболочки [4-6]. Такая интерпретация, как правило, приблизительна и имеет ограниченную область применимости. Между тем отчетливое понимание физического смысла выдаваемых прибором показателей важно как для научных исследований, так и для повышения информативности клинического обследования, что создает научную базу для совершенствования методов диагностики и оценки результатов лечения.

Для обоснованного понимания получаемых результатов необходима физически корректная и хорошо воспроизводящая данные измерений математическая модель с небольшим количеством определяющих параметров. Имеющиеся в литературе численные расчеты, основанные на громоздких конечно -элементных моделях [7; 8], содержат множество констант, в первую очередь упругих. Эти константы определяются, как правило, в измерениях на трупном материале с осреднением результатов по многим глазам. Между тем они очень значительно меняются от пациента к пациенту [9] и никогда заранее не известны для обследуемого глаза. Вязкоупругие свойства роговицы зачастую моделируются по данным опытов с характерными временами, существенно большими, чем у процессов, исследуемых ORA . Сочетание расчетов методом конечных элементов с применением техники параметрического анализа [8] не приводит к достаточно надежным результатам в силу использования моделей, хотя и многопараметрических, но не верифицированных в полной мере для изучаемых процессов.

Последовательная механическая теория реакции глаза на быстрое нестационарное воздействие разработана нами в цикле работ [10-12]. Была исследована деформация глазного яблока, роговица которого, рассматриваемая как вязкоупругое тело Фойгта, подвергается возрастающему, а затем убывающему внешнему давле- нию. Кривая «внешнее давление - время» считалась симметричной, что соответствует процессу, реализуемому в ORA. На основании математического моделирования удалось получить ряд важных выводов, касающихся физического смысла характеристик, которые могут быть определены при таком нагружении. Однако, чтобы разрабатывать рекомендации для интерпретации показаний прибора в клинике и оценивать границы его информативных возможностей, необходимо проанализировать, каким образом эти показания получаются непосредственно в приборе и по возможности учесть конкретные особенности его работы. Именно такой подгонке «идеальной» модели к реальности, с которой имеет дело клиницист, посвящена настоящая работа.

Математическая модель и абстрактная постановка задачи

Используемая модель и постановка задачи о деформировании глазного яблока под действием внешнего давления, приложенного к ограниченной области роговицы, подробно рассмотрены в [10-12]. Здесь ограничимся общей характеристикой принимаемых допущений и краткой оценкой полученных результатов.

Роговица моделируется изотропной и однородной материальной поверхностью, не сопротивляющейся изгибу. Такое представление, позволяющее описать основные особенности ее реального механического поведения, дает возможность ограничиться небольшим числом параметров, определяющих связь тангенциальных усилий с деформациями в касательной плоскости. Для моделирования рассматриваемых быстрых процессов достаточно полагать эту связь линейной, но дифференциальной: с учетом зависимости усилий не только от самих деформаций, но и от их производных по времени (скоростей деформаций). В осесимметричной постановке сохраняются лишь главные компоненты соответствующих тензоров, и определяющие соотношения, в пренебрежении объемной вязкостью, принимают вид [10; 11]:

Еi +TSi = Ат[T-VcTj -T0(l-Vc)] , (1) Ec здесь пара индексов i, j принимает значения 1,2 и 2,1;-T =(i = 1,2) касательные усилия в главных (меридиональном и перпендикулярном к нему окружном) направлениях; s. (i = 1,2) - деформации в направлениях главных осей, отсчитываемые от начального состояния не нагруженной извне роговицы, в котором она имеет форму сферического сегмента с T = T2 = То; коэффициенты E* = 5Ес и vc имеют смысл упругих модулей (модуля растяжения и коэффициента Пуассона) роговицы как двумерной упругой поверхности при медленных процессах ( 5 - средняя толщина роговицы, а Ес - ее средняя жесткость); т - время релаксации деформаций роговицы (т = ц / Ес, где ц - фойгтовская вязкость). Точкой обозначена производная по времени.

Внешнее давление p_c ( r , t ) предполагается распределенным в ограниченной апикальной области роговицы симметрично относительно оси глаза с максимумом в апексе. Вид этого распределения задается как функция координаты в соответствии с данными, имеющимися для ORA [7]. Изменение этого давления со временем определяется изменением единственного параметра, за который для определенности берется внешнее давление в апексе Pj = p_c ( 0, t ) (наибольшее по поверхности роговицы), далее называемое давлением в струе.

Склеральная область рассматривается как нульмерный упругий объект, механические свойства которого характеризуются склеральной жесткостью E [13]. Правомерность пренебрежения возможной вязкоупругостью склеры обоснована в [12]. Суммарный объем подроговичной и склеральной областей, как всегда в задачах тонометрии, считается постоянным.

Оценки показывают, что в рассматриваемом диапазоне параметров инерционными эффектами можно пренебречь [10] и процесс может рассматриваться как ква-зистатический. Соответствующая система уравнений равновесия приведена в [12].

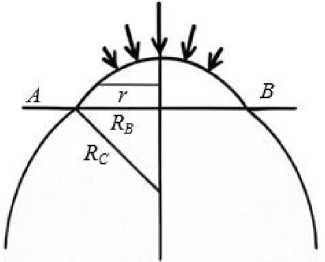
Геометрические характеристики роговицы (рис. 1, а ) принимались равными R_c = 8 мм, R_b = 5,8 мм, что соответствует стандартным для человеческого глаза значениям. Для средней толщины роговицы принималось ее нормальное значение 5 = 0,5 мм. Упругие константы E и E , а также параметр вязкоупругости т варьировались. Для коэффициента Пуассона роговицы (как двумерного объекта)’ принималось значение v_c = 0,45.

Первоначально расчеты проводились для процесса столь медленного, что его можно считать чисто упругим: т = 0 [10]. Было показано, что при некотором внешнем давлении (давлении уплощения) роговица в центральной области становится практически плоской.

Нестационарный процесс описывался в предположении, что т <<  t_c , где t_c - характерное время нагружения – разгрузки. Это допущение, мотивированное анализом экспериментальных кривых, позволило рассмотреть характеризующие этот процесс величины как поправку к стационарному (чисто упругому) решению [11].

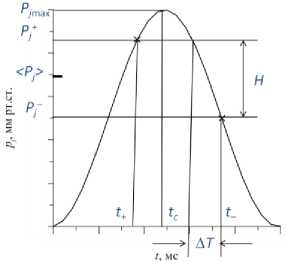
Изменение давления в струе p со временем t задавалось кривой, симметричной относительно некоторой вертикальной оси (рис. 1, б): p повышалось от нуля до максимального значения p , а затем симметрично падало снова до нуля.

Анализ процесса в такой максимально прозрачной и физически ясной постановке позволил сделать вывод об адекватности предложенной модели и получить ряд существенных результатов [11; 12]. Однако для отчетливого понимания физического смысла выдаваемых ORA данных необходимо учесть как конкретные особенности работы этого прибора, так и способ получения предлагаемых параметров.

Оценка физического смысла получаемых ORA данных

При сравнении проведенного ранее абстрактного анализа с показаниями ORA следует иметь в виду, что давление на поверхности роговицы в приборе не измеряется [1]. На дисплей выводится зависимость от времени другой величины – давления в камере, при котором выбрасывается струя в данный момент.

б

Рис. 1. Постановка задачи: а – плоскость AB отграничивает роговицу от склеральной области, r – радиальная координата, R – радиус роговицы, R – радиус основания роговичного сегмента, стрелки показывают область действия

внешнего давления; б - кривая p_} ( t ) , рассмотренная в абстрактной постановке задачи, и основные характеризующие

ее параметры: p + и p - - давления в струе при первом и втором уплощении, соответственно; <  p_ >= ( p + + p- )/2 -среднее давление уплощения; p – наибольшее прилагаемое к роговице давление;

H - корнеальный гистерезис; A T - время запаздывания второго уплощения по сравнению с первым; крестиками обозначены моменты уплощения

Будем обозначать это давление p . Измеряется оно в некоторых условных единицах ( arbitrary units, a.u. ), корректный перевод которых в какие-либо конвенциональные единицы, как будет понятно из дальнейшего, разработчиками не предлагается.

Рассмотрим сначала особенности работы прибора, не учтенные при первоначальном абстрактном анализе. Во-первых, не может существовать струи с малым (тем более нулевым) давлением. Воздействие начинается с некоторого конечного давления, величина которого не сообщается. Более того, неизвестно, одинаково ли оно во всех случаях. Во-вторых, поведение кривой р, ( t ) не задается полностью заранее: оно зависит от момента первого уплощения, происходящего при некотором давлении p, = р, + . Вскоре после достижения этого уплощения возрастание давления в струе начинает замедляться, достигая в некоторый момент времени t_c некоторого максимального значения p . Постоянство времени начала перехода к замедлению поддерживается лишь приблизительно. Затем начинается уменьшение давления, причем процесс разгрузки осуществляется таким образом, что нисходящая ветвь кривой оказывается приблизительно симметричной восходящей относительно оси t = t_c . При некотором давлении р, = р,- <  р, + происходит второе уплощение. Выдаваемая на дисплей кривая р, ( t ) имеет вид, сходный с расчетной кривой р_} ( t ) (рис. 1, б) . Однако не следует забывать, что это зависимости от времени разных величин. В различных модификациях прибора выдаваемая на дисплей кривая р, ( t ) может начинаться и заканчиваться при разных значениях p , что определяется не оговариваемым в описаниях выбором начала отсчета этой величины.

Как кривые р, ( t ) , выдаваемые ORA , так и расчетные зависимости р_/ ( t ) , имеют достаточно протяженные практически прямолинейные восходящий и нисходящий участки в окрестности точек перегиба. Анализ кривых р, ( t ) , как представленных разработчиками [1], так и полученных в разных конкретных приборах, показания которых доступны авторам, продемонстрировал, что поддерживается наклон этих участков в диапазоне к = 54 - 76 a.u. /мс (для восходящей ветви. Для нисходящей ветви наклон приблизительно равен —к . Первое уплощение всегда достигается на таком практически прямолинейном восходящем участке, тогда как второе может как находиться на прямолинейном нисходящем участке, так и попадать в область, где кривая р, ( t ) приобретает заметную вогнутость.

Данные, выдаваемые ORA, можно разделить на две группы. К первой относятся кривая р, (t) с нанесенными на ней точками, соответствующими уплощениям. По этим точкам могут быть определены времена t и давления р , при которых уплощения происходят. Это реальные физические характеристики, хотя и разной степени применимости. Если времена первого и второго уплощений t+ и t_ имеют понятный физический смысл и измеряются в миллисекундах, то связь измеряемых в условных единицах соответствующих уплощениям давлений в камере р + и р — с давлениями, испытываемыми роговицей, остается неясной и подлежит выяснению.

Вторую группу составляют величины, которые прибор вычисляет по р + и р — : внутриглазное давление по Гольдману, корнеальный гистерезис, роговично-компенсированное давление и фактор резистентности роговицы. Именно поиск возможного соответствия этих четырех характеристик различным как патологиям, так и состояниям глаза после лечебного или иного воздействия составляет содержание множества медицинских исследований, использующих ORA [14-19]. Все эти величины прибор предоставляет в миллиметрах ртутного столба.

Метод вычисления названных параметров, реализуемый прибором, - не вполне физический, а, как свойственно многим медицинским разработкам, статистический. На основании данных, полученных для группы нормальных глаз, методом линейной регрессии была статистически установлена [1; 2] линейная зависимость обоих давлений уплощения, измеренных в условных единицах, от внутриглазного давления р , измеренного для тех же глаз тонометром Гольдмана:

р. + = B ⁺ + k ⁺, р. - = B ’ + к ^— р_с (2)

причем коэффициент пропорциональности в обеих зависимостях (2) оказался по данным разработчиков [1; 2] практически одним и тем же: к⁺ = к ^— = к = 6,22 a.u. /мм рт. ст. Это позволило как рассчитывать р₀ по измеренным р * и р ^— , так и формально представлять давления р в условных миллиметрах ртутного столба: 1 «мм рт. ст.» = 6,22 a.u. Отчетливого физического смысла такой пересчет не имеет. В некоторых последующих публикациях равенство коэффициентов к ⁺ и к ^— подвергалось сомнению, и значения для них подправлялись (тоже на основе статистических данных) [3]. Мы далее следуем базовой работе [1].

Из четырех показателей, выдаваемых ORA , только корнеальный гистерезис H, введен как измеряемая в каждом конкретном опыте физическая величина:

н * = р * + р ^— (3)

Однако упомянутый выше способ его пересчета в миллиметры ртутного столба все равно основан на статистических данных.

Для выдаваемого прибором давления по Гольдману подбирается линейная комбинация p + и p - , наилучшим образом статистически соответствующая этой величине. Как известно, тонометр Гольдмана при стандартной обработке результатов измерения не всегда дает правильное истинное внутриглазное давление. Поправки к его показаниям рассчитываются по большей части на основе корреляции ошибки с центральной толщиной роговицы - параметром, который относительно легко измерить [3; 20; 21]. Дополнительные (к давлению по Гольдману и гистерезису) показатели: роговично-компенсированное давление и фактор резистентности роговицы -стремятся учесть эту корреляцию [3; 22]. Они рассчитываются тоже как некоторые линейные комбинации p + и p - , для которых статистически обосновывается в первом случае минимальная, а во втором максимальная зависимость от центральной толщины роговицы. Отчетливо определить их физический смысл затруднительно. Поскольку по p + и p - можно построить только две независимые комбинации, эти две дополнительные величины - функции двух остальных: давления по Гольдману и гистерезиса.

Для установления соответствия между давлением в камере p (измеряемым в неизвестных условных единицах) и давлением, действующим на роговицу, p_] будем исходить из двух основных допущений. Во-первых, будем предполагать, что это соответствие однозначно. Во-вторых, примем, что для нормального по механическим характеристикам глаза прибор правильно определяет давление по Гольдману, которое в этом случае равно истинному давлению. Понадобятся также эмпирические формулы (2) с k⁺ = k- = k , причем будем считать, что они справедливы и при медленном нагружении, когда глаз может рассматриваться как чисто упругий ( т = 0 и p, ⁺ = p, ^-), с тем же коэффициентом к и некоторым заранее неизвестным свободным членом В_о. Однако общий вид и границы применимости этих формул, как показано ниже, следуют из наших расчетов, и из эмпирики берется лишь значение коэффициента к = 6,22 a.u. /мм рт. ст. Нормальный глаз, как показано в [13], характеризуется упругими константами Е_с = 0,3 и E_s = 10 МПа.

Зависимость давления уплощения pjf от истинного давления p в случае упругой роговицы, полученная в [10], практически линейна и описывается формулой pff = p?о + коpо,                   (4)

где pjf 0 = 0,68 мм рт. ст., а к0 = 1,11. В соответствии с принятыми допущениями имеет место формула p.0 = B0 + kpG •                    (5)

Здесь   p 0   — значение   p, , соответствующее p_jf .

Поскольку давление, определяемое тонометром Гольдмана для нормального глаза, полагается совпадающим с истинным давлением ( p_G = p₀ ) получаем из (4) и (5), связь между давлениями p ⁰ и p , которая в соответствии с основным допущением выполняется для любых давлений p и p ,

• p, = B + к 1 p_] ,                    (6)

где

B = B 0 - k 1 p ? 0 ,                    (7)

а k = k / k₀ = 5,60 a.u. /мм рт. ст. Свободный член B_o (а следовательно, и B ), как и свободные члены B⁺ и B ^- в (2), зависит от точки отсчета давлений. Проблема оценки значений параметра B будет рассмотрена в следующем разделе. Если давление p, дано в условных «миллиметрах ртутного столба», коэффициент k j в формуле (6) пересчитывается: к = 0,90 «мм рт. ст.»/мм рт. ст. Второе слагаемое в выражении для B (7) равно 0,61 «мм рт. ст.», и им с практической точностью можно пренебрегать. В дальнейшем считается, что B = B _o, а кавычки при обозначении условных миллиметров ртутного столба опускаются.

В соответствии с (6) введенный нами гистерезис H = p ⁺ - p ^- (в миллиметрах ртутного столба) связан с гистерезисом, выдаваемым прибором, H, = p, ⁺ - p - соотношением H, = 0,9 H .

Основными для измерений являются два близких к линейным участка кривой p, (t) (или pj (t)): восходящий и симметричный ему нисходящий. Характерное время длительности каждого из них t приблизительно на порядок больше характерного времени вязкоупругости т, которое является и характерным временем затухания влияния начальных условий. Поэтому в первом приближении, достаточном для обсуждаемых расчетов, как тот участок кривой p, (t) который предшествует выходу на линейное возрастание, так и тот, который описывает переход с линейного возрастания на линейное убывание, несущественны для определения давлений уплощения. Наиболее существенны два симметричных отрезка прямых, разделенных некоторым не представляющим интереса промежутком времени. Время запаздывания AT (см. рис. 1, б) от длины этого промежутка не зависит, тогда как абсолютные значения времен утрачивают определенный физический смысл. Величина AT ценна тем, что она может быть измерена непосредственно на кривой p, (t), выдаваемой прибором (корнеограмме). Если давление первого уплощения p+ (или p +) всегда попадает на линейный участок, то давление второго уплощения p- (или p-) может оказаться в нижней части правой ветви кривой p, (t) где абсолютная величина наклона уменьшается. Поскольку формы и восходящего, и нисходящего участков кривой (за вычетом только области их сопряжения) известны заранее, определяясь конструкцией устройства, время запаздывания AT определяется по известным p + и p - и таким образом не несет дополнительной информации по сравнению с ними. Если p-попадает на прямолинейный участок, выполняется формула AT = (p,+ - p, ) / к где к = Ap, / At - абсолютная величина наклона прямолинейных участков. Если же не попадает, зависимость более сложная.

При расчетах удобно пользоваться непрерывной симметричной кривой p} (t) подбирая ее таким образом, чтобы наклон практически прямолинейных участков соответствовал поддерживаемому прибором. Мы будем использовать для кривой    p, (t)    значение к = 56 a.u. /мс, которое реализуется в доступном нам конкретном устройстве. Абсолютная величина наклона кривой p} (t) в линейных участках в этом случае равна 10 мм рт. ст./ мс. Такой наклон можно получить, например, зафиксировав длительность приложения нагрузки и подбирая ее максимальное значение p . Можно варьировать и длительность процесса. Для расчета необходимых при анализе показаний прибора величин p + , p- и AT эти вариации практического значения не имеют. В дальнейшем используется принятая в [11; 12] общая форма зависимости p} (t):

На рис. 2 центральная зеленая сплошная линия изображает зависимость давления уплощения от истинного давления при медленном нагружении (т = 0). Она практически прямая и описывается уравнением (4). Сплошные линии над зеленой соответствуют зависимостям от p давления первого уплощения, пунктирные под ней -аналогичным зависимостям для второго уплощения. При τ ≠ 0 кривые удаляются от прямолинейности тем дальше, чем больше τ. При малых τ (порядка 0,5 мс и меньше) и в области не слишком малых давлений ( p₀ >  15 мм рт. ст.) можно приближенно рассматривать их как прямые, параллельные центральной линии и одна другой.

В области малых и умеренных значений τ приближенно выполняется не зависящее от τ соотношение p_Jf =< p j >= (< p * > — в )/ k 1 ⁽ где < p j >= ⁽ p j ⁺ p — )/^{2 и} <  p. >= ( p. ⁺ + p. - ) / 2), которые позволяют при известном значении B из соотношения (4) рассчитать истинное давление p , для которого в пренебрежении слагаемым p_{jf 0} имеет место формула:

pо ~ Г < pj >= 7(< p* >- B)■          (9)

kk

В области малых и умеренных т с той же степенью точности гистерезис (т.е. н = p+ — p- ) не зависит от истинного давления p , определяясь только характерным временем вязкоупругости τ. При τ, существенно превышающем 0,5 мс, отклонением кривых от pj( t) = - /'ax

sin t

—

tc 1

2 J

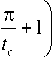
для которой теперь будем требовать p m ax / t_c ~ 6,4 мм рт. ст./мс. При этом условии функция (8) с хорошей точностью обеспечивает выбранный наклон в достаточно обширной окрестности точек перегиба. Для определенности выбирается значение t_c = 12,5 мс (как и в [11; 12]), что соответствует p_Jm ах ~80мм рт. ст. Таким образом, можно без изменений использовать те из результатов, полученных нами ранее [12], в которых принималось это значение p_jm^ .

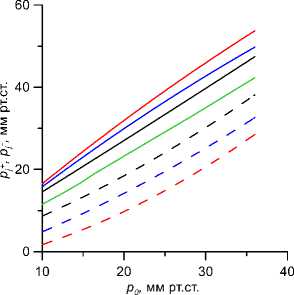
Рис. 2. Зависимость давлений уплощения от истинного давления p ₀ при Е_с = 0,3 МПа, E_s = 10 МПа. Зеленая сплошная линия соответствует давлению уплощения p_jf при т = 0, сплошные линии над ней - давлению первого уплощения p ⁺ (снизу вверх т = 0,5; 1,0; 1,5 мс), пунктирные под ней - давлению второго уплощения p ^- (сверху вниз т = 0,5; 1,0; 1,5 мс) прямолинейности и параллельности пренебрегать уже нельзя, причем с ростом т давление второго уплощения существенно быстрее удаляется от статического, чем

Расчет механических характеристик глаза по данным, предоставляемым ORA

Рассмотрим сначала показания прибора для нормального глаза, упругие характеристики которого находятся вблизи значений Е_с = 0,3 и E_s = 10 МПа [13, при разных значениях характерного времени вязкоупругости т (см. формулу (1)), отражающего соотношение между жесткостью и фойгтовской вязкостью роговицы. Эта величина введена нами в [10; 11], и статистические данные о ее нормальном значении пока отсутствуют.

давление первого. В этом случае использование формулы (9) становится недопустимым, а H перестает быть характеристикой только материальных свойств роговицы, существенно завися от давления р ₀.

Проведенное рассмотрение позволяет определить область значений параметра вязкоупругости τ, при которых приближенно справедливы формулы (2) с k⁺ = k- = k , а истинное давление р₀ определяется по давлениям уплощения независимо от т: т меньше или порядка 0,5 мс. Изучение конкретных показаний прибора указывает на то, что во многих случаях параметр т остается в области таких (умеренных) значений. Можно предположить, что и для популяции, изучавшейся в [2], величина τ в среднем находилась в этом диапазоне, для которого справедливо использованное выше допущение о прямолинейности и параллельности линий p + ( p_G ) и р, ^- ( Pg )■ В этом диапазоне в случае нормального по упругим характеристикам глаза ( E_c и E_s вблизи 0,3 и 10 МПа соответственно) выполнена и использованная выше формула (5). Будем пока рассматривать именно глаза, удовлетворяющие обоим этим условиям.

Вернемся к формуле (6), определяющей связь давлений р, и Pj , для которой осталось неоцененным значение константы B , определяемое выбором начальных значений р, , заложенным в программное обеспечение конкретной модификации прибора.

Переопределим давление р, по формуле р ‘ = р, - B . Штрих далее опускаем. Тогда из (9) получаем для такого переопределенного давления соотношение:

P G =< Р * >= ( Р + + Р - ) / 2, (10)

где pG - давление по Гольдману, выдаваемое прибором, а давления р + и р- даны в условных миллиметрах ртутного столба. Формула (10) соответствует заявленному словесно разработчиком утверждению, что внутриглазное давление по Гольдману определяется как среднее двух давлений уплощения [1]. По определенным давлениям р + и р- рассчитываются (так, как указано выше) и две дополнительные характеристики: роговично-компенсированное давление и фактор резистентности роговицы [23].

Теперь соотношение (6) принимает вид:

Р * = ^0,9 P j ,                     (11)

где давления измерены в миллиметрах ртутного столба. Таким образом, при рассмотренном переопределении давления р , соответствующем специальному выбору начала его отсчета (разному для разных модификаций прибора), это давление оказывается пропорциональным давлению, приложенному к роговице.

В соответствии со сформулированным выше основным допущением полученная для достаточно узкого диапазона механических характеристик глаза формула (6) и следующая из нее при переопределенном давлении р формула (11) остаются справедливыми и для значений E , E и т, в этот диапазон не попадающих.

Рассмотрим теперь более общий случай, когда глаз остается нормальным по упругим константам ( Е_с = 0,3 , E_s = 10 МПа), но т существенно превышает 0,5 мс, и формула (9) несправедлива. Формула (11) верна и в этом случае. Поскольку стандартные алгоритмы расчета давления по Гольдману р и гистерезиса H не учитывают зависимость от τ, по формально выдаваемым прибором значениям этих величин в соответствии с формулами (3) и (10) могут быть восстановлены давления р + и р, ^-, а затем из соотношения (11) давления р ⁺ и р ^- а также их полусумма <  р . > и разность H . Истинное давление теперь не пропорционально <  р . >, а зависит как от <  р . >, так и от т.

а                                                  б

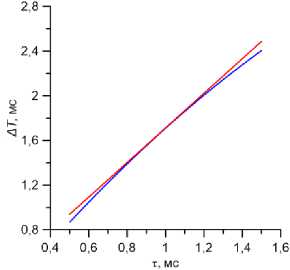
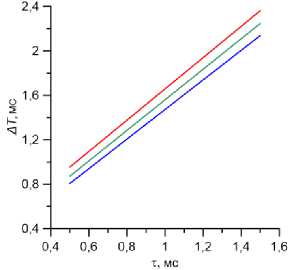
Рис. 3. Зависимость времени запаздывания AT от времени релаксации деформаций т для нормального (а - Ес = 0,3 и Es = 10 Мпа при р0 = 12; 32 мм рт. ст.) и очень жесткого (б - Ес = 0,9 и Es = 40 Мпа при р0 = 12; 20; 32 мм рт. ст.) глаза при истинных давлениях (снизу вверх)

Зависимости <  p_j >, H и времени запаздывания A T от р₀, т и упругих констант подробно исследовались в [12]. В частности, в этой работе показано, что для нормального по упругим константам глаза время запаздывания A T от р₀ практически не зависит (рис. 3, а ), и определяется, таким образом, только параметром τ. Как уже упоминалось выше, время A T может быть снято непосредственно с кривой р. ( t ) (корнеограммы). Поэтому для такого глаза можно оценить истинное давление (с учетом зависимости от т) по кривым р_а ( < р. > , т ) (или Ро (< Р- >, т) ) и A T (т) . Параметр т может быть также рассчитан (не прибегая к непосредственным измерениям на корнеограмме) по гистерезису и среднему давлению уплощения, определенным по показаниям прибора. На рис. 4 представлены (сплошные кривые для нормального глаза) зависимости н ( < р. > ) при разных т, полученные численным исключением истинного давления р₀ из зависимостей H (т, р ₀) и <  р_ >  ( т , р ₀), рассчитанных в [12]. При известных н и <  р >  определяется кривая, на которую попадает соответствующая точка, и выбирается значение т, соответствующее этой кривой.

После того как параметр вязкоупругости τ одним или другим способом определен, можно выбрать кривую р о ( < Р _j > , т ) (или р ₀ (< р * >, т)) (рис. 5, а ), соответствующую этому т, и найти истинное давление р .

Таким образом, использование непосредственно получаемых ORA параметров р + , р - и A T , из которых лишь два независимых, позволяет в предположении нормальности глаза по упругим свойствам ( E_c = 0,3 и E_s = 10 МПа) рассчитать как характерное время вязкоупругости т, так и уточненное истинное давление р (по сравнению с рассчитываемым прибором на основании статистических данных). С возрастанием т истинное давление p , соответствующее каждому измеренному

• < р. >  (или <  р. > ), увеличивается. Различие в значениях p , определяемых при разных τ (из реально наблюдаемого диапазона) для одного и того же <  р. >  больше для низких давлений и меньше для высоких, не превышая 2 мм рт. ст. Выбор средней кривой на рис. 5, а, уменьшит ошибку до 1 мм рт. ст.

Отдельную задачу составляет учет влияния упругих констант, которых в первом приближении две: роговичная и склеральная жесткости E и E соответственно. Перейти от выдаваемых прибором величин к р + и р- (и следовательно, к <  р. >  и H) по формулам (3), (10) и (11) по-прежнему возможно. Расчеты зависимостей величин <  р. >  и H от E_c и E_s выполнены в [12], но найти еще и упругие константы лишь по двум независимо определяемым параметрам нельзя. Для корректного определения всех четырех характеристик

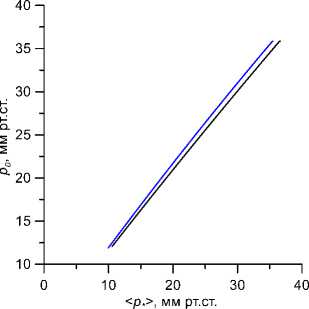
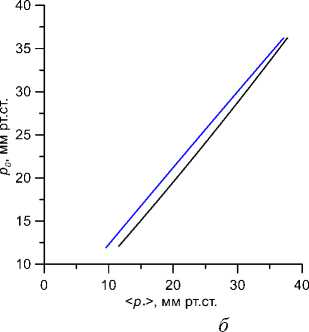
а

Рис. 5. Зависимость истинного давления р ₀ от выдаваемого ORA среднего давления <  р, > («давления по Гольдману») для нормального ( а - E c = 0,3 и E s = 10 МПа при т = 0,6) и очень жесткого ( б - Е_с = 0,9 и E_s = 40 Мпа при т = 1,4 мс) глаза при различных временах релаксации деформаций (снизу вверх)

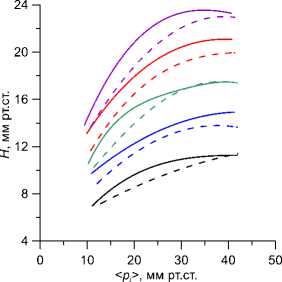
Рис. 4. Зависимость гистерезиса н от среднего давления <  р. >  для нормального ( Е_с = 0,3 и E_s = 10 МПа - сплошные линии) и очень жесткого ( Е_с = 0,9 и E_s = 40 МПа - пунктирные линии) глаза.

Каждая пара линий одного цвета (сплошная и пунктирная) соответствует одному и тому же значению времени релаксации деформаций т: снизу вверх т = 0,6; 0,8; 1; 1,2; 1,4 мс механических свойств и механического состояния глазного яблока: (Ec, Es, т и p0) необходимы дополнительные измерения. Однако определенные выводы можно сделать, опираясь только на данные ORA.

На рис. 3-5 наряду с зависимостями для стандартного глаза показаны аналогичные кривые для глаза с очень жесткими роговицей и склерой: Е_с = 0,9 и E_s = 40 МПа. Значительное увеличение жесткости глазных тканей происходит с возрастом и особенно заметно для глаз с глаукомой [5; 24-27]. В отличие от нормального глаза (см. рис. 3, а ), для жесткого (см. рис. 3, б ) влияние давления на зависимость A T ( т ) становится более заметным: значения τ при 12 и 32 мм рт. ст. различаются на величину порядка 1 мс при малых A T и порядка 2 мс при больших. При том же значении A T параметр т оказывается теперь больше, чем значение этого параметра для нормального глаза. Разница составляет примерно 0,2 мс при низком давлении и уменьшается с его возрастанием. При очень высоком давлении эта разница практически исчезает. Таким образом, использование зависимости A T ( т ) для нормального глаза при нахождении параметра τ для глаза жесткого приводит к занижению, хотя и не слишком значительному, значения этой величины, тем большему, чем ниже давление. К некоторому занижению значения τ приводит и использование соответствующих нормальному глазу сплошных кривых на рис. 4 вместо пунктирных, построенных для глаза жесткого.

Что касается кривых р0 (< р* >), то они при переходе от нормального к жесткому глазу меняются совсем незначительно. Это связано с тем, что роговичная и склеральная жесткости влияют на эту зависимость разнонаправленно [12], и, таким образом, их влияние имеет тенденцию к взаимной компенсации. Для жесткого глаза разница между истинными давлениями р , соответству ющими одному и тому же < р* > при разных т, немного больше, чем для нормального, но остается небольшой, достигая при низких давлениях 3 мм рт. ст.

Заключение

Анализатор реакции глаза ( ORA ) разрабатывался в первую очередь как тонометр. Предполагалось, что по измеряемым в этом приборе характеристикам двух уплощений (при нагружении и разгрузке) можно получить более адекватную информацию об истинном внутриглазном давлении, чем в обычном пневмотонометре, где используется информация только о первом уплощении [1]. Так как из двух измеряемых давлений уплощения может быть получено две независимых величины, был введен в дополнение к истинному давлению второй параметр: корнеальный гистерезис, который обычно истолковывается как мера вязкоупругости роговицы.

Физически содержательная модель нагружения глаза быстропеременным давлением, приложенным к роговице, разработана и исследована в наших публикациях [11; 12]. В настоящей работе параметры этой первоначально абстрактной модели максимально приближены к характеристикам ORA . В результате сопоставления с приведенными в литературе данными статистической

Signal

• -    ^^,0

• - 72 ь

• ■ ^п ¹ I ' I ' I ¹ I ¹ I I I ' I ¹ I I I ¹ I ¹ I ' I ' I ¹¹1

113.2 И 10.3 Irtq                    tof

TIME lOPcc lOPg CH CRT                              ORA

Рис. 6. Информация, выдаваемая при конкретном измерении ORA (воспроизведено с дисплея конкретного прибора). По оси абсцисс - время (в мс). Зеленая кривая представляет зависимость от времени давления p * , измеренного в условных единицах. Синие квадратики на ней указывают моменты уплощения. Остальные линии характеризуют интенсивность оптического сигнала, отраженного от поверхности роговицы: красные -непосредственно измеренную, синие - после заложенной в программное обеспечение процедуры сглаживания. Внизу слева - рассчитанные прибором показатели: роговично-компенсированное внутриглазное давление ( IOPcc ), внутриглазное давление по Гольдману ( IOPg ), корнеальный гистерезис ( CH ) и фактор резистентности роговицы ( CRF) . Вверху слева - оцененный прибором показатель формы волны WS . Для идеальной формы отраженного сигнала WS =10

обработки конкретных измерений установлены соотношения, связывающие показания, выдаваемые прибором, как с давлением, непосредственно действующим на роговицу, так и с физически содержательными характеристиками механических свойств и механического состояния глазного яблока.

В публикациях [11; 12] было показано, что величина корнеального гистерезиса зависит не только от вязкоупругих свойств роговицы, определяемых характерным временем релаксации деформаций (параметром вязкоупругости) τ, но и от внутриглазного давления и, в меньшей степени, от упругих свойств глазных тканей. Поэтому в настоящей работе мы рассмотрели возможность эффективной оценки с помощью ORA наряду с истинным внутриглазным давлением не гистерезиса, а параметра τ, непосредственно отражающего вязкоупругие свойства роговицы.

Рассмотрено механическое поведение при обследовании ORA глаз двух типов: нормальных, для которых упругие константы имеют средние для здоровых глаз значения, и обладающих очень жесткими склерой и роговицей, что наблюдается, в частности, при глаукоме [5; 27].

Для нормального глаза с учетом статистических данных выдаваемое прибором «давление по Гольдману» верно отражает истинное давление в глазу, если параметр вязкоупругости меньше или порядка 0,5 мс. Этот параметр для такого глаза может быть эффективно оценен по информации, предоставляемой прибором. В случае, если он выходит за пределы умеренных значений (что, как показано нами ранее [12], для многих глаз имеет место), поправка к показанию прибора может быть рассчитана. Расчеты показывают, что результат при этом меняется не слишком существенно: как правило, не более, чем на 2 мм рт. ст. Столь же незначительна поправка к значению показателю давления для глаза с повышенной жесткостью, лишь в исключительных случаях достигая 3 мм рт. ст.

Проведенное рассмотрение носит идеализированный характер. Определение давлений уплощения p + и p- в ORA осуществляется с не слишком высокой точностью. Одна из причин этого несомненна и отмечалась разработчиками [1]: оптический сигнал (рис. 6), по данным которого эти давления определяются, размыт и имеет нерегулярную форму. В связи с этим в поздних модификациях прибора выдается некоторый показатель формы волны (WS, waveform score) [28], и рекомендуется выполнять несколько измерений, выбирая то, для которого WS наилучший. Разброс измеряемых величин при повторных измерениях оказывается весьма значительным. Имеются и другие факторы: в их числе не вполне точная повторяемость прилагаемого струйного воздействия и особенности исполнения измерений, присущие их конкретному исполнителю и пациенту. Ошибка выполняемых прибором измерений за- частую превосходит поправки, вносимые учетом влияния конкретного значения параметра τ или повышенной жесткостью глазных тканей. Таким образом, «давление по Гольдману», определяемое ORA, дает вполне адекватную, хотя и не слишком точную оценку величины истинного внутриглазного давления.

Параметр вязкоупругости τ, определяемый по данным, предоставляемым ORA , представляет собой реальную характеристику вязкоупругих свойств роговицы и поэтому может оказаться более представительным диагностическим критерием, чем корнеальный гистерезис, который зависит не только от этих свойств, но и от других величин, в первую очередь от внутриглазного давления. Возможность оценки этого параметра представляется наиболее существенной ценностью ORA , тогда как невысокая точность определения истинного давления не дает этому прибору заметных преимуществ при тонометрии. Оценка значений параметра τ для нормальных глаз и при патологиях потребует специальных исследований.

В настоящей работе рассмотрение проводилось в предположении, что механические свойства роговицы эффективно характеризуются единственным упругим и единственным вязкоупругим параметрами. Такое допущение недостаточно в случае, если роговица сильно неоднородна пространственно, что возможно как в силу индивидуальных особенностей (например, при заметном превышении ее толщины в центральной области над средним значением этой величины) или вследствие патологий, так и в результате хирургического вмешательства, например, после лазерной коррекции зрения. Для статического нагружения влияние такого рода неоднородности было исследовано в рамках разработанного нами общего подхода в [29]. Не рассмотрена возможная ситуация, когда роговица сильно ослаблена в сравнении со склерой. Исследование таких случаев предполагается выполнить в дальнейшем.