Полулинейные модели соболевского типа. Неединственность решения задачи Шоуолтера - Сидорова

Обширный класс моделей математической физики основан на полулинейных неклассических уравнениях или системах уравнений в частных производных, неразрешенных относительно производной по времени [17, 24]. Такие уравнения принято называть уравнениями соболевского типа [1,4,5,16,38,40]. Уравнения представленного класса и начальные задачи для них не удается исследовать классическими методами в следствие возможного вырождения оператора при старшей производной, поэтому для их исследования требуется развитие новых и модификации уже известных методов исследования [31, 34, 35, 41, 42]. Представленная работа носит обзорный характер и содержит полученные ранее результаты исследований научной школы, созданной и возглавляемой профессором Г.А. Свиридюком, по изучению нелинейных уравнений или систем уравнений, фазовые пространства которых имеют особенности ( k -сборку Уитни). Рассмотрим математические модели, основанные на уравнениях или системах уравнений соболевского типа:

– системе уравнений распределенного брюсселятора [2, 18, 37]

– системе уравнений Плотникова [22, 23]

Г V t = V ss - W ss ,

[ 0 — v + w _ss + 5w — ew ³ ,

– уравнении Хоффа [12]

(A + A)v t — a i v + a 2 V³ + ... + a k v^

Все перечисленные выше системы уравнений будут рассмотрены в цилиндре Q х R + , где Q С R n - ограниченная область с границей д^ класса C ^го , с однородным граничным условием Дирихле

v(s,t) — 0, w(s,t) — 0, (s, t) G д^ х R+, в случае систем уравнений (1), (2), или с граничным условием Робена

∂v∂w

(тт- + Av) — 0, (——+ Aw) — 0, (s,t) G д^ х R+,

∂n∂n в случае системы уравнения (3), или с однородным граничным условием Дирихле

v(s, t) — 0, (s,t) G дfi х R+, в случае уравнения (4).

Математические модели (1), (5); (2), (5); (3), (6) и (4), (7) описывают процессы, протекающие в различных предметных областях (более подробно о процессах, моделируемых приведенными задачами, будет сказано в первой части статьи), но принадлежат к одному классу полулинейных моделей и будут исследованы в рамках абстрактного полулинейного уравнения соболевского типа

Li — Mu + N(u), ker L — { 0 } .                         (8)

Вектор-функцию u G C 1 (R + ; U), которая удовлетворяет (8), будем называть решением уравнения. В силу вырожденности уравнения (8) решение задачи Коши

u(0) — u o                                        (9)

для него не существует при произвольном начальном значении u o G U [19,36]. В работах [13, 27, 36, 39] было предложено рассматривать неклассические начальные условия, которые позволяют учесть возможное вырождение оператора L . Рассмотрим начальное условие Шоуолтера – Сидорова

L(u(0) — u o ) —0,                                   (10)

которое является обобщением условия Коши и эквивалентно ему в случае невырожденного уравнения (kerL — {0}). Рассмотрение условия (10) позволяет избежать трудностей изучения задачи Коши, однако возможна неединственность решения задачи (8), (10) [3, 19, 27]. Метод фазового пространства Г.А. Свиридюка [25,28] позволяет найти пути решения перечисленных проблем. Он заключается в редукции исходного сингулярного уравнения к регулярному u1 = F (u), определенному не на всем пространстве, а на некотором специальным образом построенном его подмножестве M, понимаемом как фазовое пространство (многообразие). Дальнейшее изучение структуры (простоты или наличия особенностей) фазового многообразия M позволяет не только находить достаточные условия существования решения задачи (8), (9), но и исследовать вопрос единственности решения задачи (8), (10).

К настоящему времени метод фазового пространства успешно применен к исследованию уравнения (8) в случае (L,p) -orpaHU4eHHoro, (L,p) -секториального и (L,p) -радиального оператора M [14,15,19,32], а также в случае s -монотонного и р -коэрцитивного оператора N и фредгольмового оператора L [19, 26]. Перечисленные классы уравнений описывают широкий спектр неклассических моделей математической физики. В линейном случае ( N = O ) применение метода фазового пространства позволило разработать теории вырожденных (полу)групп операторов и показать, что фазовое пространство основного уравнения совпадает с образом разрешающей (по-лу)группы операторов [30].

В обзорной статье [19] были приведены условия для абстрактного уравнения (8), при которых фазовым многообразием уравнения служит простое гладкое банахово многообразие, из чего следует единственность решения задачи (8), (10). Совсем иная ситуация получается в случае, когда фазовое многообразие уравнения (8) лежит на многообразии, содержащем особенность, например, k -сборку Уитни [3, 33, 34]. Будем говорить, что уравнение G(q, u) = 0 определяет k -сборку Уитни над открытым множеством U С U , если существуют функции g ₀ , g 1 ,..., g k Е C ^го (U ; R) такие, что это уравнение эквивалентно уравнению

0 = g o (u) + g i (u)q + ... + g k (u)q ^k + q ^k+1 V u Е U ‘ .

В этом случае проекция u o на M вдоль ker L может иметь несколько образов, и соответственно задача (8), (10) будет иметь несколько решений. Этот феномен был впервые отмечен в [27].

Исследование случая, когда фазовое многообразие уравнения (8) лежит на гладком банаховом многообразии, имеющем особенности, началось с работы [3] для математических моделей реакции-диффузии. Г.А. Свиридюком и его ученицей Т.А. Бокаревой [3] были найдены условия существования особенностей типа k-сборок Уитни фазового пространства уравнений класса реакции-диффузии, а также было показано, что фазовое пространство системы уравнений распределенного брюсселятора (1) в случае 61 = 0 содержит 1-сборку Уитни (1-сборку Уитни также принято называть складкой). Г.А. Свиридюком и его учеником В.О. Казаком [32] были найдены условия, при которых фазовое многообразие уравнения Хоффа (4) является простым банаховым многообразием. Позже в работе Г.А. Свиридюка и его ученицы И.К. Три-неевой [33] были найдены условия на параметры уравнения Хоффа, при которых фазовое многообразие содержит 2-сборку Уитни. В работе Г.А. Свиридюка и его ученицы А.Ф. Гильмутдиновой [11] было показано, что фазовое многообразие системы уравнений Плотникова может содержать особенности типа k-сборок Уитни, и найдены условия существования нескольких решений для задачи Шоуолтера – Сидорова. В работах Н.А. Манаковой и О.В. Гавриловой [9, 20] было продолжено исследование особенностей фазового многообразия моделей (1) и (2) и найдены условия при которых существует одно или несколько решений задачи Шоуолтера – Сидорова.

Статья содержит обзор работ Г.А. Свиридюка и его последователей по изучению морфологии фазовых пространств уравнений соболевского типа, выявлению особенностей фазового многообразия основного уравнения, из которых следует неединственность решения задачи Шоуолтера – Сидорова, и состоит из 2 основных частей. В первой части приведены условия на параметры изучаемых моделей, при которых фазовые многообразия являются простыми, из чего вытекает единственность решения задачи Шоуолтера – Сидорова. Во второй части приведены условия, при которых фазовое многообразие рассматриваемой модели содержит особенность ( k -сборку Уитни), из чего вытекает неединственность решения задачи Шоуолтера – Сидорова.

• 1.    Простые фазовые многообразия. Единственность решения

  • 1.1.    Вырожденная модель деформации двутавровой балки

В Q х R + рассмотрим вырожденное уравнение Хоффа (4), моделирующее выпучивание двутавровой балки, находящейся под постоянной нагрузкой. При этом искомая функция v = v(s,t) , (s, t) G Q х R + , моделирует отклонение балки от вертикали, параметры a i G R \ { 0 } , i = 1,...,к, характеризуют свойства материала балки, параметр A G R + характеризует нагрузку на балку. Рассмотрим условие Шоуолтера -Сидорова

(A + A)(v(s, 0) - v o (s))=O, s G Q,                       (11)

с краевым условием (7) для уравнения (4).

О

Введем пространства H =W2 (Q), Y = W2 1 (Q), X = L2(Q), B = L2k (Q), построим операторы

(Lv, u) = У (Avu

-

V v • V u)ds,

V v,u G H ,

Ω

(Mv, u) = a 1

vuds,

Ω

^ v,u G H ,

(N(v),u) = y"(a ₂ v ³ + ... + a _{k - 1} v ^{2k 3} + a _k v ^2k 1 )uds Ω

V v, u G B.

В силу предложенного построения операторы L,M G L (H; Y) , причем оператор L фредгольмов, при этом при всех значениях a 1 G R \{ 0 } оператор M L -ограничен, а оператор N G C ^го (H; Y) , если к = 1, 2 при n = 4 или к = 1, 2, 3 при n = 3 или k G N при n = 1, 2 .

Обозначим через {^к} собственные функции однородной задачи Дирихле для оператора (—A), занумерованные по неубыванию, а через {vk} соответствующие им соб- ственные значения. Построим множество

M =

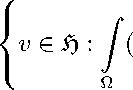
a 1 + a ₂ v ²

+ ... + a k v ^{2k 2} )v^ _k ds = 0, A = v k

Теорема 1. [32] Пусть k = 1, 2 при n = 4 или k = 1, 2, 3 при n = 3 или k E N при n = 1, 2. Тогда

• (i)    если ker L = { 0 } , то фазовым пространством уравнения (4) служит все пространство H ;

• (ii)    если ker L = { 0 } , все коэффициенты a i E R \{ 0 } , i = 1,...,k , одного знака, то фазовым пространством уравнения (4) служит простое многообразие M , моделируемое подпространством H 1 = { v E H : (v, ^ _k ) = 0, A = v k } ;

• (iii)    если все коэффициенты a i E R \{ 0 } , i = 1,..., k , одного знака, то существует и притом единственное решение задачи (4), (7), (11).

• 1.2.    Модель Плотникова

В полуполосе (a, b) x R + рассмотрим систему уравнений Плотникова (3) с краевым условием

(u s — Au)(a, t) = (u s + Au)(b, t) = 0, t E R ₊ ,                     (12)

и начальным условием Шоуолтера – Сидорова

v(0) = v o .

Математическая модель (3), (12) является одной из моделей фазового поля в рамках мезоскопической теории в предположении, что время релаксации равно нулю. Параметры в и 5 характеризуют фазовый переход. Здесь u = col(v,w) , v = v(s,t) , w = w(s,t) , (s,t) E (a, b) x R ₊ , параметры A, 5 E R ₊ ,e E R .

Введем банахово пространство H = W 21 (a, b) x W 21 (a, b), гильбертово пространство X = L 2 (a, b) x L 2 (a, b), скалярное произведение которого определим как

b

b

[u,Z] = J vids + [

wnds = (v,i) + (w,n),

a

a

где Z = col(i, n), а через ( • , • ) обозначим скалярное произведение в L 2 (a, b) . Обозначим через Y пространство, сопряженное к X относительно двойственности [ • , • ]. Построим линейные операторы L, M : X ^ Y :

[Lu, Z]

b vξds,

a

v,Z E X;

bb

[Mu, Z] = — j v s i s ds — A (v(a)i(a) + v(b)i (b)) + j w s i s ds + A (w(a)i(a) + w(b)i (b)) —

b

— j w s n s ds - X (w(a)n(a) + w(b)n(b)), v, Z E H. a

Отметим, что оператор L E L (X; Y) , а оператор M E C l(X; Y) , dom M = H . При этом оператор M L -секториален.

Обозначим через { ν _k } собственные значения спектральной задачи

— ^ ss = v^, s E (a,b),

^s(a) = A^(a), ^.(b) = —A^(b), занумерованные по неубыванию, а через {ϕk} соответствующие собственные функции, ортонормированные в смысле скалярного произведения (•, •). Построим нелинейный оператор

b

[N (u),Z ] = J (v + 5w — ew3)nds a и положим dom N = B = L4(a,b) x L4(a,b). В силу предложенного построения при всех фиксированных значениях параметров в, 5 E R оператор N E C^(B; B*).

Построим пространство X _a = X 0 ф х а , где x a = L 4 (a, b) x { 0 } , X ? = { 0 } x W 2¹ (a, b) , тогда выполняются плотные и непрерывные вложения

H ֒ → X α ֒ → B ֒ → X ֒ → Y .

Построим фазовое многообразие M, которое примет вид bb

M = ^{{ u E X a :} /^vnds = /(w . , . - ^5wn ■ B^ws ■ xHaw) ■ w(^b)ⁿ(b)) } . aa

Теорема 2. [11] Для всех фиксированных значений параметров в, X E R + , 5 E (0, v 1 ),

• (i)    фазовым пространством уравнения (3) служит простое банахово C ^∞ -многообразие M ;

• (ii)    для любого u 0 ∈ X α существует единственное решение задачи (3), (12), (13).

• 1.3.    Вырожденная модель распределенного брюсселятора

В Q x R + рассмотрим вырожденную систему уравнений распределенного брюссе-лятора (1), моделирующую периодическую химическую реакцию, которая в случае

е2 = 0 примет вид | vt = a?Av + Bi — (в2 + 1)v + v2w,                      (1 5) [ 0 = a2Aw + B2v — v2w, с граничным условием (5) и начальным условием Шоуолтера – Сидорова

v(0) = v o .

Здесь функции v = v(s,t) и w = w(s,t) описывают концентрации реагентов, члены a 1 Av, a 2 Aw характеризуют диффузию реагентов (в силу закона Фики), а 1 , a ₂ G R \{ 0 } — коэффициенты диффузии, параметры в 1 , в 2 G R описывают концентрации исходных реагентов, которые предполагаются постоянными.

Аналогично параграфу 1.2 введем в рассмотрение банахово пространство H = О ¹            о ¹

H 1 х H 2 = W 2 (Q) х W 2 (Q), гильбертово пространство X = L 2 (Q) х L 2 (Q), скалярное произведение которого определим как [u, Z] = (v,^) + (w,n), где u = (v,w(Z = (C,n), при этом ( • , • ) - скалярное произведение в L 2 (Q). Обозначим через Y пространство, сопряженное к H относительно двойственности [ • , • ]. Построим линейные операторы L,M : H ^ Y следующим образом:

^[Lu,z] = ^(v,<), ^{u,z G} H,

^{[Mu,Z ]} = ^{- a} 1 ⁽v s i ,^ S i ) ^{- a} 2 ⁽w S i ,n s i ), ^{u,Z G} H.

В силу задания операторы L, M обладают свойствами L G L ( H , Y), M G L ( H ; Y).

Замечание 1. Заметим, что здесь и далее выполняется соглашение Эйнштейна о суммировании по повторяющимся индексам.

В силу предложенного построения при всех фиксированных значениях параметров a 1 , a ₂ G R \{ 0 } оператор M будет L -секториальным. Далее построим нелинейный оператор

[N(u), Z ] = (в 1 - (в + 1)v + v 2 w, <) + №v - v ² w, n)

и положим dom N = B = L 4 (Q) х L 4 (Q), B * = L 4 (Q) х L 4 (Q). Для всех фиксированных значений параметров в 1 , в 2 G R, n <  4, оператор N G C ^ro (B; B * ) .

О1

Построим пространство X _a = X 1 ф X a , где X 0 = { 0 } х W 2 (Q), X a = X ^a х { 0 } , X ^a = L 4 (Q). Следует отметить, что при n <  4 справедливо плотное и непрерывное вложение

H ^ в ^ X ^ в * ^ Y.

Построим фазовое многообразие M , которое примет вид

M _£ 2 = { u G X a : (a 2 W s i ,n s i ) + (v 2 w,n) = (e 2 v,n) } .

Теорема 3. [9] Для всех фиксированных значений параметров a 1 G R \{ 0 } , а ₂ G R + , в 1 ,в 2 G R, n <  4,

• (i)    фазовым пространством системы уравнений (15) служит простое C ^го - многообразие M ε ₂ ;

• (ii)    для любого u ₀ G X _a существует и единственно решение (5), (15), (16).

• 1.4.    Вырожденная модель распространения нервного импульса

В цилиндре Q х R+ рассмотрим вырожденную систему уравнений Фитц Хью -Нагумо (2) в случае 61 = 0, которая примет вид j 0 = a1Av + e12W — в1ГУ,

[ w t = a 2 Aw + e 22 W — в 2Г У — w 3

с граничным условием (5) и начальным условием

w(0) = w ₀ .                                   (18)

Математическая модель (2), (5) моделирует распространение волн возбуждения, лежащих в основе передачи нервных импульсов в биологической системе. Здесь w = w(s, t) — функция, описывающая динамику мембранного потенциала, v = v(s, t) - медленная восстанавливающая функция, связанная с ионными токами, а 1 ,а ₂ G R \{ 0 } , в ₁₁ , в ₁₂ , в ₂₁ , в 22 G R — фиксированные параметры, характеризующие: в 11 , в ₁₂ — порог возбуждения и его скорость, α 1 – электропроводность среды, α 2 – реполяризацию среды.

О 1            о 1

Введем банахово пространство H = H 1 х H 2 = W 2 (Q) х W 2 (Q), гильбертово пространство X = L 2 (Q) х L 2 (Q). Обозначим через Y пространство, сопряженное к H относительно двойственности [ • , • ]. Построим линейные операторы L, M : H ^ Y следующим образом:

^[Lu,z] = (w,^, ^{x,z G} H ,

^{[Mu,Z ]} = ^{- a} 1 ⁽v S i ^,Z S i ) ^{- a} 2 ⁽w s i ,n s i )•

В силу построенной конструкции L G L ( H , Y), M G L ( H , Y). Отметим, что для всех фиксированных значений параметров а 1 ,а ₂ G R \{ 0 } оператор M L -секториален.

Далее построим нелинейный оператор

[N(x), Z ] = (в^ - e il V, €) + ^22 W - e 21 V - W 3 , П)

и положим dom N = B = B i х B 2 = L 4 (Q) х L 4 (Q), B * = B * 1 х B 2 = L 4 (Q) х L 4 (Q) . При всех фиксированных значениях параметров в 12 , в 22 , в 11 , в 21 G R, n <  4, оператор N G C ^ro (B; B * ) .

Построим пространство X _a = X 0 ф X a , где X 0 = W 2¹ (Q) х { 0 } , X a = { 0 } х Х ^а , X ^a = L 4 (Q). Следует отметить, что при n <  4 справедливо плотное и непрерывное вложение

H ^ X a ^ B ^ X.

Построим фазовое многообразие

M _£ 1 = { x G X a : (a i V s i ,< S i ) + (в1^,<) = (в 12 w,<) } .                (19)

Теорема 4.  [20] Для всех фиксированных значений параметров a2 G R\{0}, в21,в22 G R, а1,в11,в12 G R+, n < 4,

• (i)    фазовым пространством системы уравнений (17) служит простое C ^го - многообразие M ε ₁ ;

• (ii)    для любого u ₀ G X _a существует и единственно решение (5), (17), (18).

• 2.    Фазовые многообразия с особенностями. Неединственность решения

  • 2.1.    Вырожденная модель Хоффа

В Q х R+ рассмотрим уравнение Хоффа (4) в случае k = 2 с краевым условием (5) и начальным условием (11). Пространства H, Y, X, B и операторы L, M, N были построены в п. 1.1. Построим проектор I — Q = (•,^1), где ^1 G kerL, ||^1||L2(Q) = 1, и множество

M = { v G B : (Mv + N (v), ^ _i ) = 0 } .

Замечание 2. Здесь и далее будем рассматривать только такие собственные функции фк спектральной задачи с однородным условием Дирихле для оператора (—А), которые соответствуют однократным собственным значениям νk, т.е. таким, для которых выполняется условие dimker(v I + А) = 1.

Построим подпространство B ^± = { v ^± G B : (v ^± ,^ 1 ) = 0 } и представим вектор v = qV 1 + v ^± , тогда множество M C ^ -диффеоморфно множеству

M q = < (q, v ^± ) G R x B : q ³ || ^ i || B + 3q 2 j ^ ^ v ^± ds+

Ω

+q ^У ^ i (v ^± ) 2 ds + а а₂ 1 ^ + У ^ 1 (v ^± ) 3 ds = 0

.

Выделим во множестве M подмножество

M ‘ = { v G B : (M^ i + N V ^ i , ^ i ) = 0 } П M.

Множество M ^′ C ^∞ -диффеоморфно множеству

M q = \ (q, v ^± ) G R x B ^± : 3q ² || ^ i || B + 6q j ^ i v ^± ds+

I                                  ) ^Q                            (21)

+3 У ^ ! (v ^± ) ² ds + a ₁ a -¹ = 0/ П M ‘ .

Ω

Теорема 5. [33] Пусть 1 <  n <  4 , a _i a ₂ < 0, A = v _i . Тогда

• (i)    любой вектор £ G ker L \{ 0 } не имеет (M + N V ) -присоединенных векторов, если v G M \ M ‘ ;

• (ii)    любой вектор £ G ker L \{ 0 } имеет точно один (M + N V ) -присоединенный вектор, если v G M ‘ \ B ^± .

Рассмотрим уравнение Хоффа (4) при k = 2 в случае Q = (0, l) :

Avt + vsst = aiv + a2v3, s G (0, l), t G (0, T)•

Для нашего случая задача Шоуолтера – Сидорова примет вид:

A (v(s, 0) — vo(s)) + (vss(s, 0) — vo(s)) = 0, s G (0, l).

Построим фазовое многообразие уравнения

M = {v G B : (aiv, ^i) + (a2v3, ^i) = 0}.

Уравнение, определяющее множество M, является кубическим уравнением общего ll вида aq3 + bq2 + cq + d = 0, здесь a = ||^i HB, b = 3 J ^1 v1 ds, c = 3 J y^v1 ds + a1a-1,

l d = J y1(v1)3ds, p =

3ac — b ² 9a ²

_ 1 / 2b ³ e = 2 \27a 3

—

b + d Y Res ( 3a ²    a

r, v ¹ ) = p ³ + e ² ,

l

R(q,v ^{± )} = Vll^i Il B + +6q

/ 0

^v ¹ ds + 3

l

I ^ 1 (^{v ± ) 2}

ds + a i a2 •

Построим множества

B + = {v g B ¹ : Res(q,v ¹ ) > 0 } ,

B - = {v g B ¹ : Res(q,v ¹ ) < 0 } .

Теорема 6. [10] Пусть a ₁ a ₂ < 0, A = v ₁ . Тогда

• (i)    множество M r образует 2-сборку Уитни;

• (ii)    для любого v ₀ G B ¹ П B - существуют три решения задачи (7), (22), (23); (iii) для любого v ₀ G B ¹ П B + существует одно решение задачи (7), (22), (23).

• 2.2.    Модель Плотникова

В полуполосе (a, b) х R + рассмотрим математическую модель Плотникова (3), (12) с условием Шоуолтера – Сидорова (13). Пространства H , X , B , X _α , Y и операторы L, M и N были построены в п. 1.2. Рассмотрим случай, когда 5 = v ₁ , где v ₁ - первое собственное значение спектральной задачи (14).

Если положить v = v1 + ry1, w = w1 + qy1, то фазовое многообразие M, построенное в п. 1.2, определяется системой из двух уравнений bb

J v ^ n ^ ds = J(w ^ n^" — v ₁ w^±n^± + в (w ^± + qy ₁ ) 3 П ^± )ds+

+A(w ¹ (a)n ¹ (a) + w ¹ (b)n ¹ (b)),

в 1r = fwi1 + q^1)3^1ds, a где вместо n сначала подставлено n1, а потом y1. Здесь числа r, q G R, а y1 - собственная функция задачи (14), отвечающая собственному значению ν1 и нормированная в смысле L2(a, b); векторы v1 G B1, w1, n1 G H1, где B1 = {v G B1 : (v, y1) = 0}, H1 = {w G H2 : (w,^1) = 0}.

Перейдем к рассмотрению второго соотношения в (25), которое представим в виде

b

b

b

q ³ || ^ 1 |l L 4 + 3q 2 IУ 3 w¹ds + 3q J y 1 (w ¹ ) ² ds + J ^(w ¹ ) ³ — в ¹ r = 0.

aaa

Уравнение (26) является кубическим уравнением общего вида aq3 + bq2 + cq + d = 0, где a = H^iIlL^Q), b = 3 Jw±^1 ds, c = 3J(w±)M ds,

ΩΩ d = j ^i(w±)3ds - e2ir,p = 3ac 2 b , e = 1 f^b^ - ^ + dA ,       (27)

q                            9a ²          2 \27a ³    3a ² a/

Res(q, w ^± ) = p ³ + e ² .

Как хорошо известно из формул Кардано, уравнение (26) имеет от одного до трех действительных корней, причем оно имеет точно два корня, если вдобавок к нему выполняется

R(r, w ^± )

= г2|И^ + 2r

b j ^lw±ds +

b j V2(w±)2

= 0.

a

a

Введем в рассмотрение множество P = { u G M : R(r, w ^± ) = 0 } .

Для удобства дальнейшего рассмотрения введем следующие множества:

H 0 = { w G H 2 : R(r,w ^± ) = 0 } ,

H + = { w G H 2 : R(r, w ^± ) > 0 } , H ₂ = { w G H 2 : R(r, w ^± ) < 0 } .

Теорема 7. [11] При любых в, X G R ₊

• (i)    множество M образует 2-сборку Уитни;

• (ii)    для любого v ₀ G B 1 П H - существует одно решение задачи (3), (12), (13);

• (iii)    для любого v ₀ G B 1 П H + существуют три решения задачи (3), (12), (13).

• 2.3.    Вырожденная модель распределенного брюсселятора

В Q х R + рассмотрим вырожденную систему уравнений распределенного брюссе-лятора (1) в случае 6 1 = 0 , которая примет вид

Г 0 = a i Av + в 1 - (в 2 + 1)v + v ² w, [ w t = a ₂ Aw + e 2 v — v ² w,

с краевым условием (5) и начальным условием

w(0) = w ₀ .

Пространства H , X , B , Y и операторы M и N были построены в п. 1.3. Отличительной особенностью данной задачи является задание оператора

^[Lu,z ] = ^(w,n⁾, ^{u,z G} H .

Отметим, что для всех фиксированных значений параметров a 1 ,a ₂ G R \{ 0 } оператор M будет L -секториальным.

О 1

Построим пространство X _a = X ^¹ ф X a , где X a = { 0 } х X ^a , X ^ = W ₂ (fi) х { 0 } , X ^a = L 4 (^). В силу свойств оператора N и получившихся вложений справедливо N G C ^ (X a ; Y) .

Построим фазовое многообразие

M _£ 1 = { u G X a : (a i V s i ,^) = (в 1 - (в + 1)v + v ² w,() } .             (30)

Возьмем произвольную точку u = (v,w) G X _a , представим u = (v ¹ + q^ k ’W ¹ ), где v ¹ G H t , w¹ G (X ^a ) ¹ , H ^ = { v G H 1 : (v ¹ , V k ) = 0 } , (X ^a ) ¹ = { w ¹ G X ^a : (w ¹ , V k ) = 0 } . Тогда множество (30) может быть определено следующим образом

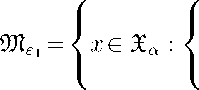
^(a 1 L Л¹ ) = ^(в - № + l^{)v ±} ,( ^{± ) +} +(^ + q^ k ^w ¹ ,C 4

- №,V k ) = ((v ¹ + q^ k ) ² W^V k )

При этом первое соотношение в (31) получено в случае, когда подставлено £ = £ ¹ в (30), а второе соотношение в случае £ = V k .

Рассмотрим второе соотношение (31) и, преобразуя его, получим:

q ² J* w¹ Vkds + 2q J(v¹ ) 2 w¹

ΩΩ

V k ds + j (v ¹ ) 2 w¹V k ds + У в 1 V k ds = 0.       (32)

Ω

Ω

Заметим, что уравнение (32) является квадратным уравнением вида ar ² + br + c = 0 ,

где

a = У w¹V k ds, b = 2 У (v ¹ )²w ¹ v k ds, c = У (v ¹ ) 2 w ¹ V k ds + У e 1 V k ds.

Ω

Ω

Ω

Ω

Построим функционал Res(v ¹ ) : H ¹ ^ R :

2 W ¹ V k ds + j в 1 V k ds

Ω и рассмотрим множество

(H ¹^ = { v ¹ G H ¹ : Res(v ¹ ) > 0 } .

Для любого v ¹ , принадлежащего множеству (H ¹ ) + , уравнение (32) будет иметь два различных решения вида

— 2 J (v ¹ ) ² w ¹ V k ds — д/Res (v ¹ )

q - =

q + =

2 w ¹ V ³ _k ds

Ω

— 2 J (v ¹ ) ² w ¹ V k ds + д/Res (v ¹ )

² J ^{w 1} V k ^ds

Ω

Построим множества

9№             I ^(aiv ^s1 ’^ ^s1 ) = ^(e - ^(e 2 ^{+ 1)v 1 + (v 1 +} q - V i ^{) 2 w 1} ,(

M , 1 _ -1« ^{G X a} .| v = q _ (v ^G )V k + v ¹                             /'

™           J ^(a i ^v1 ’^)=^{(e — (e} 2 ^{+1)v 1 +(v 1 +}q + V i ^{) 2 w 1 ,}< ^{1 )}, 1

M„ + =|^{u G X a} .| v = q _{+ (} v ± )V k + v ¹                             /■

В том случае, когда начальные значения лежат во множестве M _{£ 1} \ (M _{£ 1 +} U М _{£ 1} _ ), их принято называть точками складки Уитни фазового пространства. Наличие в фазовом многообразии особенностей предполагает, что уравнение может иметь несколько решений или не иметь их совсем. Построим множества

(H ^ ) _ = { v ^± G H ^ : Res(v ^± ) < 0 } ,

(H ^ ) o = { v ^± G H ^ : Res(v ^± ) = 0 } .

Теорема 8. [9] Для всех фиксированных параметров a ₁ ,a ₂ G R \{ 0 } , в 1 ,в 2 G R, n <  4,

• (i)    фазовое пространство M _{£ 1} _ U M _{£ 1 +} содержит 1-сборку Уитни;

• (ii)    для любого u ₀ G (H ^ ) ₊ x (X ^a ) ^± существует два решения задачи (5), (28), (29);

• (iii)    для любого u ₀ G (H ^ ) ₀ x (X ^a ) ^± существует одно решение задачи (5), (28), (29);

• (iv)    для любого u ₀ G (H ^ ) _ x (X ^a ) ^± задача (5), (28), (29) не имеет решения.

• 2.4.    Вырожденная модель распространения нервного импульса

В Q x R + рассмотрим вырожденную систему уравнений Фитц Хью - Нагумо (2) в случае е ₂ = 0 , которая примет вид

Г V t = a i Av + в 12 W - в11 v, [ 0 = a ₂ Aw + в 22 w — в ₂₁ v — w 3

с граничным условием (5) и начальным условием

v(0) = v o .

Пространства H, X, B, Y и операторы M и N были построены в п. 1.4. Отличительной особенностью данной задачи является задание оператора lLu,zI = (v,z),u,z G H.

Отметим, что для всех фиксированных значений параметров a ₁ , a ₂ G R \{ 0 } оператор M L -секториален.

Построим пространство X _a = X ° ф X a , где X 0 = { 0 } x W jj Q), X a = X ^a x { 0 } . Для всех фиксированных значений параметров e ij G R, i, j = 1, 2, n <  4, оператор N G C ^ (X a ; Y) .

Построим фазовое многообразие

M _£ 2 = L G X a : - (v,() = f-^в 2² W + 1- W 3 ,() + f^²W si ,( s?) ) .      (36)

β 21      β 21              β 21

Рассмотрим случай в 22 = a ₂ v ₁ , положим

О

X ^a± = { v ^± G X ^a : (v ^± ,^ ₁ ) = 0 } , H 2 = { w ^± G W 2¹ (Q) : (w ^± ,^ ₁ ) = 0 } .

о

Если v G X ^a1 и w G W 21 (fi) представить в виде v = v ¹ + r^ 1 и w = w ¹ + qv 1 , где r, q G R, то множество

/             /

/ - v ¹ < ds^s = J ( ^—|1 w ¹ ^ ^{± +} ' w ^{1 +}

Ω

M _e 2 = x G X a :

Ω

+^^{(w ±} + qv i ^{) 3} (^±) β 21

— в 21 Г = I (w ¹ + qV i ) ³ V i ds

ds,

Ω

Перейдем к рассмотрению второго соотношения в (37) и, преобразуя его, получим:

q ^{3 ||} V iH L ₄ (Q) + V I w^ds + 3q j (w^fv l ds + j V i ⁽w ^{1 ) 3} ds + ^e 2i r = 0.      (38)

Уравнение (38) является кубическим уравнением общего вида aq3 + bq2 + cq + d = 0, где a = NViC^ b = 3 Jw^lds c = 3 jCw^vlds

ΩΩ r                         3ac — b2      1 7 2b3     bc d\ d = /V1 (w )ds— e2ir,p=^02-,e = 2(27-3— 322 + a).

Res(q, w¹) = p ³ + e ² ,

^R(q.w^r) = q ² ^ v i ^ L 4 (q) + 2q J V 3 ^{w ±} ds + J v ! ^{(w ± ) 2} ds.

Построим множества

H 0 = { w G H 2 : R(q, w¹) = 0 } , H + = { w G H 2 : Res (q, w¹) > 0 } , H- = { w G H 2 : Res(q, w ¹ ) < 0 } .

Теорема 9. [20] При любых а ₁ ,в ₁₁ ,в 1₂ G R, a ₂ , в 21 G R ₊ , в 22 = a ₂ v 1 , n <  4,

• (i)    фазовое пространство M ε ₂ содержит 2-сборку Уитни;

• (ii)    для любого v ₀ G X ^a QH - существует одно решение задачи (5), (33), (34);

• (iii)    для любого v ₀ G X ^a QH + существует три решения задачи (5), (33), (34).

Авторы сердечно поздравляют своего учителя, наставника, профессора Георгия Анатольевича Свиридюка с юбилеем и благодарят его за предоставленные возможности, безграничное терпение, щедрость и заботу.

Работа проводилась при финансовой поддержке Министерства науки и высшего образования Российской Федерации, грант FENU-2020-0022 (2020072ГЗ).