Ползучесть полиэтилена высокой прочности при различных режимах нагружения

Для проведения расчетов на ползучесть элементов конструкций из материалов с реологическими свойствами (противофильтрационные полимерные экраны, облицовки, крепления, нежесткие покрытия в гидротехническом и в дорожном строительстве, силовые и декоративные стержни, балки, пластины и оболочки, в частности трубопроводы в промышленном и гражданском строительстве) необходимо располагать уравнениями механических состояний. Уравнения могут быть построены чисто в феноменологическом плане, либо в их основу могут быть положены механические или физические модели описываемых деформационных процессов.

Обзор литературы

Важным классом конструкционных материалов с реономными свойствами, исследованию которых посвящена литература [1-10], отличающаяся значительным разнообразием подходов к расчету деформаций и времени разрушения, являются полимерные и полимерные композиционные материалы, металлы и сплавы при высоких термомеханических нагрузках, а также при воздействиях среды и некоторых энергетических полей. Ряд материалов, используемых для изготовления элементов конструкций, рассчитанных на длительный срок эксплуатации, испытывает старение, отражающееся на сопротивлении деформированию и разрушению.

Постановка задачи и актуальность исследования

В общем случае полная деформация, развивающаяся при длительном нагружении, является суммой четырех составляющих: мгновенноупругой, мгновеннопластической, вязкоупругой и вязкопластической [1, 2, 11-17].

Разделение полных деформаций на реономные и склерономные в начале процесса нагружения является в определенной степени условным. В данной работе под прямой ползучестью понимается рост деформаций во времени при постоянно снижающихся нагрузках. При нарастании нагрузок от нуля до тех значений, которые по расчету отвечают заданным истинным напряжениям ползучести, возникают малые вязкоупругие и вязкопластические деформации, выделение которых из общей деформации является почти неразрешимой задачей. Однако с этой условностью приходится мириться, и она не мешает составлению уравнения механических состояний. При малых временах нагружения соотношение между составляющими деформации оказывается не совсем правильным, но при этом общий итог должен все же отвечать действительности, с другой стороны, учет всех четырех составляющих деформации, если только опыты не указывают на явное отсутствие каких-либо из них (например, вязкопластической и мгновеннопластической составляющих), придает уравнению состояний большую гибкость, позволяющую удовлетворительно описывать практические любые релаксационные процессы.

Полимерные материалы могут иметь в общем случае как сдвиговую, так и объёмную ползучесть. Однако при плоском напряженном состоянии проявляется, главным образом, сдвиговая ползучесть, протекающая при условии постоянства объёма, которое при линейном напряжённом состоянии полиэтилена высокой плотности (ПЭВП) проверялось в работе [11]. Ввиду этого будем считать, что в наших опытах ползучесть носит преимущественно сдвиговой характер, а объёмная ползучесть имеет место в незначительной степени или отсутствует.

В данной работе построено уравнение механических состояний, в основе которого лежит результат опытов по деформированию тонкостенных трубчатых образцов полиэтилена высокой плотности (степень кристалличности по методу Германса-Вейдингера 58%) при различных кратковременных и длительных режимах нагружения осевой силой и внутренним давлениям [18, 19]. Испытания полимерных материалов проводились в широком диапазоне напряжений, включая предельные напряжения [20].

Описание исследования

Для подбора приближенных законов мгновенноупругого и мгновеннопластического деформирования использовались данные опытов на монотонное нагружение ( со скоростью ^^а ‘/^_т = 0.1 ^ 0.3 МПа/с) с регистрацией и последующим мгновенным разгружением образца. При этом замерялись мгновенноупругие и остаточные (мгновеннопластические) деформации. Опыты проводились при нескольких уровнях интенсивности напряжений и различных видах напряженного состояния. Зависимость мгновенноупругих деформаций от интенсивности напряжений o_t для исследуемых материалов аппроксимировались в следующем виде [21]:

Construction of Unique Buildings and Structures, 2015, №12 (27)

2(1+V) Oi

=----------

■ =₃ E„ (1- ∗∗

где ^ - интенсивность мгновенноупругой деформации.

Зависимость мгновеннопластических деформаций E ^МП материалов от интенсивности напряжений представлена в виде [21]:

mat

E МП ₌ у ( e ° ^∗ -1)

Для исследования вязкоупругой составляющей деформации ползучести ставились опыты на обратную ползучесть (возврат после разгрузки). Член уравнения, описывающий зависимость от времени вязкоупругой составляющей полной деформации, при пропорциональном нагружении записывался в виде:

£ВУ =∫ A(-)A( )к(т-6) de j0    °∗

Эта зависимость требует подобия кривых обратной ползучести. Экспериментальные данные показывают, что условие подобия приблизительно выполняется. Ядро к (т) аппроксимировалось суммой двух экспонент:

К (т)= A_Te"^{T /} Mi + Л₂е ^T/ М2

Подбор постоянных упрощается тем обстоятельством, что при больших временах обратной ползучести графики скоростей в полулогарифмических координатах являются практически прямыми, следовательно, описываются одной экспонентой с относительно большим временем релаксации Д2 . После подбора первой экспоненты определяется вторая с малым временем релаксации.

Точность описания обратной ползучести можно, естественно, повысить путем увеличения числа экспонент в ядре К (T) . Однако, во избежание значительных усложнений расчетов, сохраняем в выражении ядра всего две экспоненты.

Для подбора функции f 1(^ ) использовался график зависимости E ВП_/∫ ^ К (T-0) de относительно — при её аппроксимации: ^{∗ ∗}

^л( ; ∗      ; ∗ ⁾ ”

Вид функции f 2( Ms) установлен путем сравнения результатов испытаний при различных видах девиатора истинных напряжений (Ms – параметр Лоде). Рассеивание экспериментальных данных оказывается довольно значительным (основное отклонение ^/*2 ( Ms) = 0,156 при коэффициенте корреляции z = 0,97) в случае линейной аппроксимации функции f 2( Ms):

A( Us )= a ^- Ьц₅                                    (6)

Обратимся к другому члену уравнения механических состояний, описывающему зависимость от времени вязкопластической составляющей полной деформации. График этой зависимости получен путем вычитания из полной деформации ползучести при стационарном нагружении трех, ранее выделенных, составляющих. Как показывают расчеты, полученные кривые необратимой прямой ползучести приблизительно подобны, что в соответствии с [11] позволяет применить для аналитического описания вязкопластических деформаций соотношение вида:

£   ⁼A(7)A( Us ) В ( T ) dr ,

∗ где: Et - скорость интенсивности вязкопластических деформаций и в(т) - убывающая функция времени.

Интенсивность вязкопластических деформаций определяется при стационарном нагружении интегралом

£ВП =∫"A( S )A(Ms ) В (т) dx .

Функция в(т) находилась по графику скорости вязкопластической деформации при ai =  ∗ . Эта функция была аппроксимирована зависимостью:

В ( x )=Д₃е ⁽ т-т   .

Методика определения функций f 3( — ) иf 4( Bs) остается такой же, как и при определении функций ∗ f 1( or" ) иf 2( Bs). Функция f 3(^) на участке достаточно больших деформаций удовлетворительно аппроксимировалась линейной зависимостью (коэффициент корреляции 0,92)

A⁽ ; ∗ ^)=K( ∗   ⁶ ).

При меньших отклонениях, как и при т < т _∗ , вязкопластические деформации вообще отсутствуют, а ползучесть происходит только за счет вязкоупругой составляющей деформации.

Функция f 4 ( Bs ) аппроксимировалась линейным соотношением вида (основное отклонение ∆ f 4 ( Bs )= 0, 15)

A(Ms)= d. - IBs ^.

Таким образом, выделены и описаны все составляющие полной деформации исследуемого материала. Полное уравнение механических состояний в интенсивностях при стационарном нагружении имеет вид:

2 (1+V) °i ,  / m—

^E‘ ₌2 ₃ E, (1- ) ∗∗     ' ^{(     ∗}

-1)+∫( a - bBs ) c — [ A_Te Bi + A₂e B2 ] d9 +

+∫ ⁽ d ^- IBs ⁾ К ( ^-

8 )[Л₃е ⁽ T-T ⋅ )/ ∝ ] dx .

Уравнение (12) в компонентах девиаторов напряжений и деформаций записывается в следующем виде:

=

(1+V) Sij

Eq (1-

³ Sij ( ) ^{+2 Y (} ∗∗

3 fT           /ст,\пГ   —L          1

e °∗-1)+ ₂ ∫ ( a - bBs ) c ( )[ A_Te Bi + A₂e B2 ] d9 +

+ I ∫ ⁽ d ^- IBs ⁾ К ( ? ^-Z V                  о ∗

8 )[ A₃e ⁽ T-T ⋅ )/ ∝ ] dx ,

где для полиэтилена высокой плотности (ПЭВП) получили:

Eq =960 МПа; a∗∗ =30 МПа; v = 0․48; у=1·10 -4 ;m = 2,5; a∗ = 10МПа; a = 0․6; b = -0․64; c = 0․07; n=4; Л1=8․5⋅10 -4 ; A2 =1․6⋅10 -4 ; Bi = 110с; B2 = 2250с; d = 0․7; I = 0․3; 8 = 1․37; К = 3․4; A3 =11⋅10 -6 ; ∝=1․25⋅104с

В более общем случае пропорционального нагружения первое слагаемое в выражениях (12, 13) сохраняет тот же вид, а второе слагаемое сохраняет формально тот же вид с дополнительным условием, что в качестве

мы должны вносить наибольшее значение интенсивности напряжений на рассматриваемом участке нагружения.

Закон мгновеннопластического деформирования при сложном напряженном состоянии и непропорциональном нагружении формировался в соответствии с обобщенной теорией пластического течения

МП 3 de_t МП Stj de_tj ⁼ 2

где de_t МП ^{∗ =}√^∑ Ае_ц МП² - приращение инварианта Одквиста.

Для случая ступенчатого (нестационарного) режима нагружения применялся обобщённый закон вязкопластического деформирования:

^i ^ВП = £f 3 (^MWtW + ^d^ ^f₃ (^(_к)В(; - 0)d0 (15)

Проверка применимости уравнений (12, 13) механических состояний осуществлялась на нестационарных режимах статического нагружения исследуемого материала (ПЭВП). Режимы настационарного статического нагружения приведены на рисунках 1-3. Здесь же показаны зависимости интенсивности истинных деформаций от времени. Сравнение экспериментальных и расчетных данных проводилось для ПЭВП при девяти режимах нагружения. Оно показывает, что расчет в целом воссоздаёт процесс ползучести при сложном режиме нагружении с удовлетворительной точностью. Исследование источников наблюдаемых расхождений показало, что эти расхождения связаны, прежде всего, с недостаточно точной аппроксимацией функции К(т) . Уравнения механических состояний в виде (12) и (13) дают адекватное описание деформационных процессов рассматриваемого материала при сложных ступенчатых режимах статического нагружения и может быть использовано для прогнозирования деформаций ползучести [23-25].

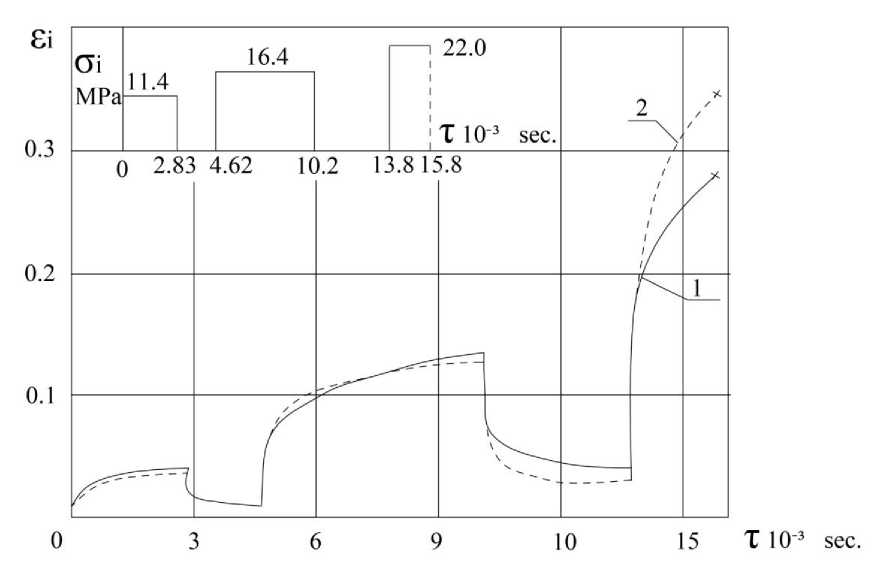
Рисунок 1. Режим нестационарного статического нагружения и кривые ползучести ПЭВП

( <г / ст₆ = 1 ): 1- опытные кривые; 2 - расчетные кривые

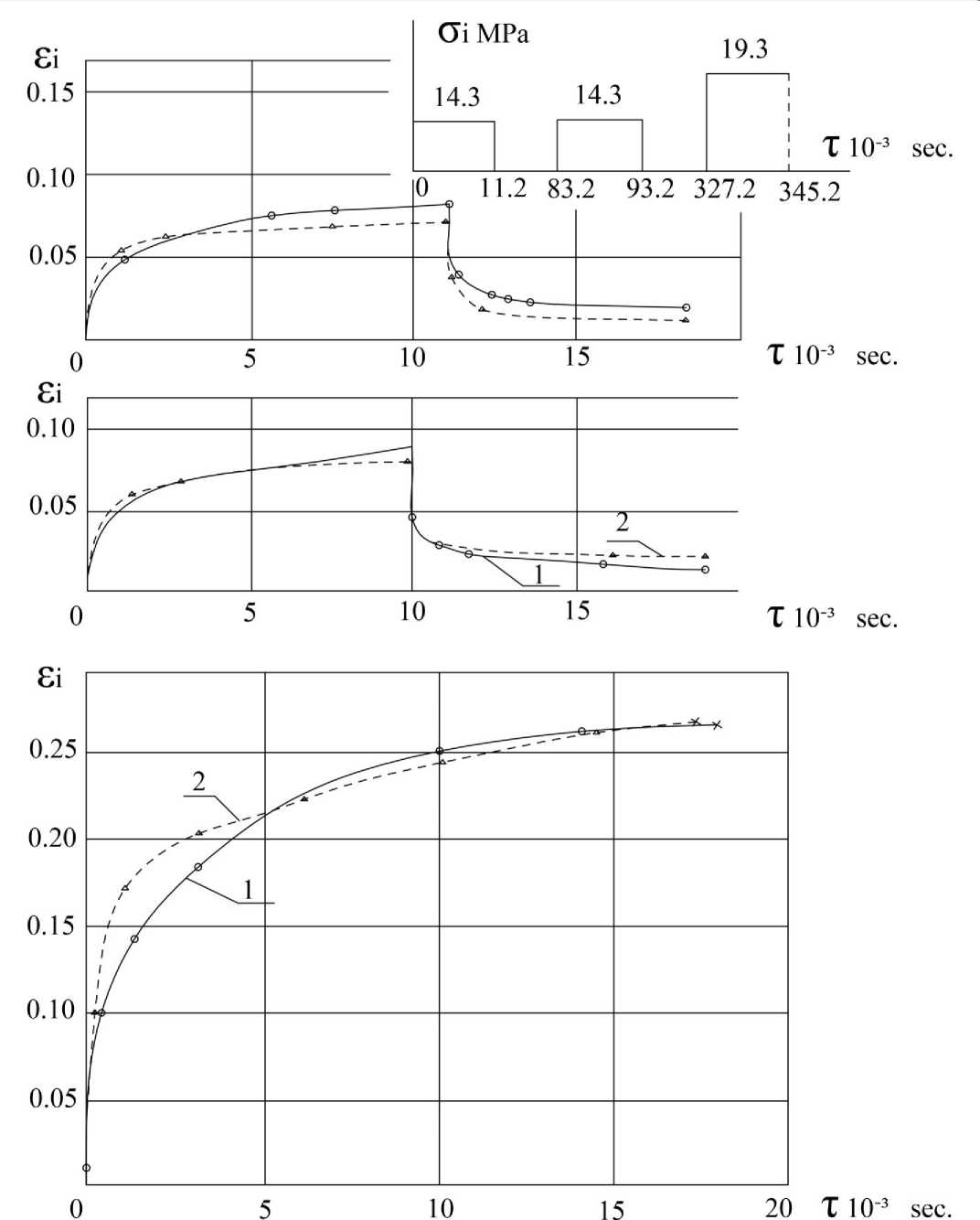
Рисунок 2. Режим нестационарного статического нагружения и кривые ползучести ПЭВП (с т * / с т _е = 0,75 ): 1- опытные кривые; 2 - расчетные кривые

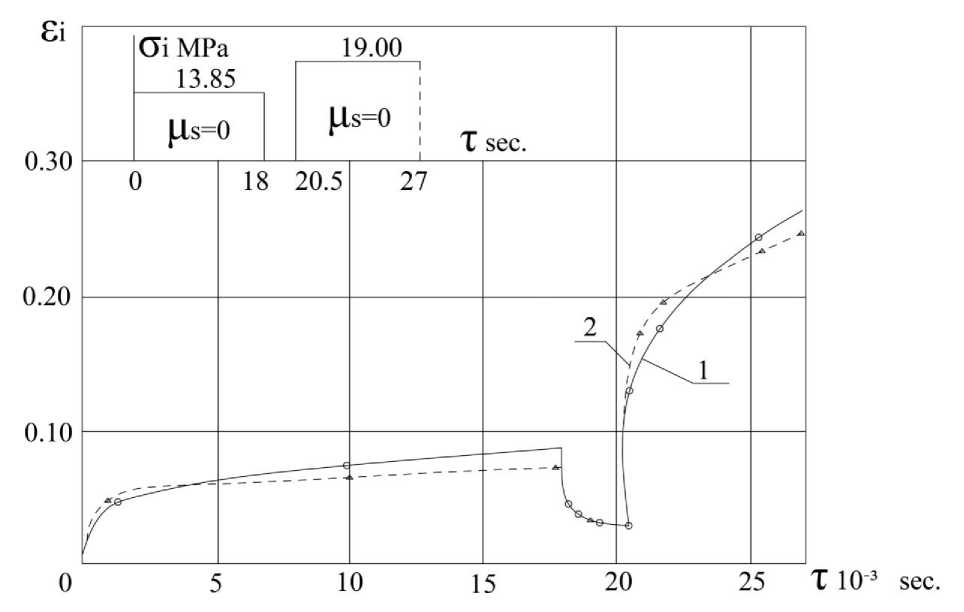
Рисунок 3. Режим непропорционального статического нагружения и кривые ползучести ПЭВП:

1 – опытные кривые; 2 – расчетные кривые

Постоянные и функциональные параметры уравнений механических состояний полимерных и полимерных композиционных материалов существенно зависят от температуры [2]. Если от температуры зависят лишь временные параметры уравнений, то при некоторых дополнительных условиях устанавливается температурно-временная аналогия, по которой процесс неизотермического нагружения сводится к изотермическому в приведенном времени. В области физической нелинейности материала от температуры зависят не только временные, но и силовые параметры уравнений (12) и (13). В таких случаях предложен прием преобразования ступенчатого неизотермического режима нагружения к эквивалентному изотермическому режиму [2, 13, 14]. Конечные значения вязкоупругой и вязкопластической составляющих полной деформации получаются наложением ряда импульсов нагружения, приложенных в действительные или приведенные моменты времени.

Естественное старение (время старения т _с ) и поврежденность (мера П) при длительном нагружении влияют на процесс ползучести материала и на величину предельной деформации [22]. Накопленные деформации и повреждения изменяют соотношения между составляющими полной деформации при ступенчатых (с частичными или полными промежуточными разгрузками) режимах нагружения. При длительной разгрузке после нагружения в материале происходит ряд конкурирующих процессов, в частности залечивание повреждений и естественное старение. Уравнения (12) и (13) включают функциональные параметры (зависящие от т _с и П), которые устанавливаются на основе результатов дополнительных опытов [23, 25, 26]. Учет меры повреждений П оказывается эффективным при описании деформаций, непосредственно предшествующих моменту разрушения.

Очевидной является попытка применения предлагаемых уравнений механических состояний к условиям циклического напряженного состояния [11, 27, 28]. Мгновенные составляющие полной деформации вычисляются по максимальным за период цикла напряжения. Вязкоупругая может быть вычислена непосредственно подстановкой переменных значений напряжений. Для расчета вязкопластической составляющей предлагается ряд подходов [11, 27]. В ряде работ предлагается использовать понятие приведенного времени. Приведенное время связано с физическим временем при помощи некоторого масштабного коэффициента. Для построения теоретически обоснованного уравнение механических состояний исследование продолжается.

Для расчета деформаций ползучести при циклическом нагружении использовали эмпирическую зависимость, которая приводит к удовлетворительному описанию экспериментальных данных. Уравнение состояний представляется в виде:

I _a.m ax ---                        /„.таххП _

⁽ a-pц^е   *» -1|y+( + -bb ^_s ) X ₂c(-  ) $₀K(t-

** ^{7    0}                    (16)

0)d0 + ( d - /^^(^^ - 8) Г BW t , o**

где эмпирический коэффициент Я₂ (для ПЭВП Я₂ = 0,882 ), а функции К(т) и В(т) определены при проведении статических испытаний. Расчетные деформации ползучести ПЭВП показаны на рис.4-6. Расчет дает относительно удовлетворительное описание ползучести в случае нестационарного циклического нагружения. Исключения имеют место, когда интенсивность деформаций ползучести достигает зоны предельных деформаций на первых ступенях нагружения. Принципы построения наиболее распространенных уравнений механических состояний, в том числе и предложенных в данной работе, изложены в учебном пособии [29]. Изложенные в работе методы расчётов на ползучесть могут быть использованы при оценке прочности водоводов и адаптированы для моделирования процесса разрушения сцепления арматуры с бетоном [30-32].

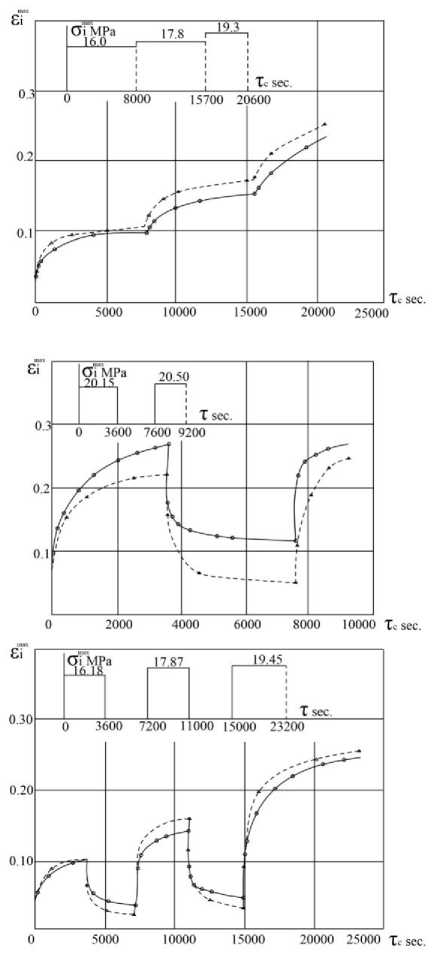
Рисунок 4. Режим нестационарного нагружения с частотой 5 Гц и кривые ползучести ПЭВП при σ соотношении ( n =x =1): 0 – опытные и ∆ - расчетные кривые

σθ

Construction of Unique Buildings and Structures, 2015, №12 (27)

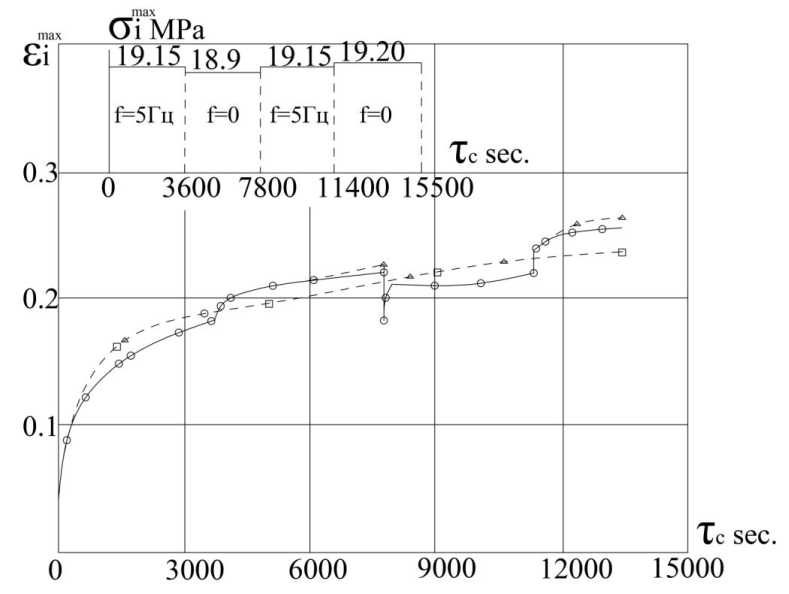
Рисунок 5. Режим смешанного нагружения и кривые ползучести ПЭВП: 0 – опытные и □,∆- расчетные кривые

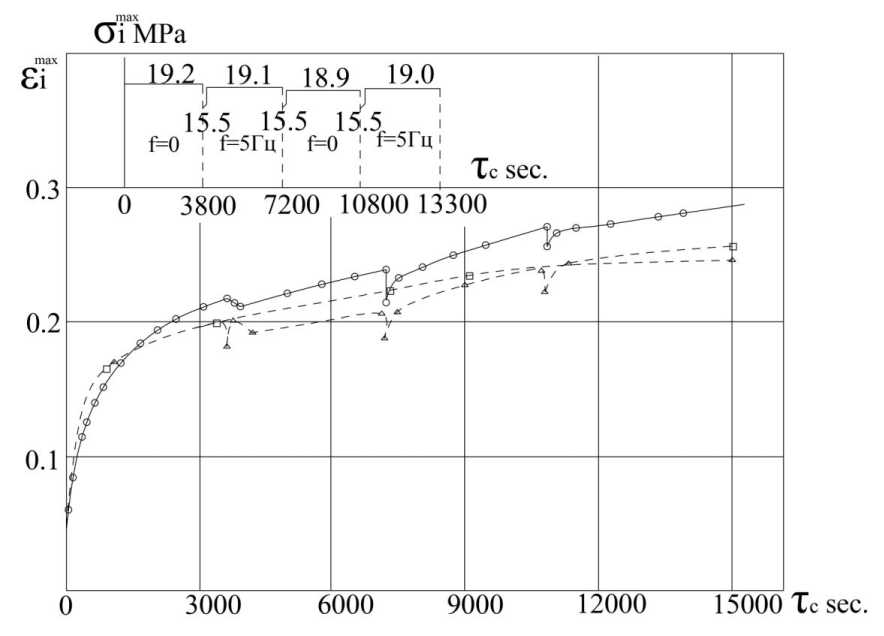
Рисунок 6. Режим смешанного нагружения и кривые ползучести ПЭВП: 0 – опытные и □,∆- расчетные кривые

Заключение

• 1.    Деформации ползучести полиэтилена высокой плотности (ПЭВП) при статическом стационарном и нестационарном нагружении удовлетворительно описываются уравнением механических состояний, учитывающим мгновенноупругую, вязкоупругую, мгновеннопластическую и вязкопластическую составляющие деформации с использованием условия постоянства объёма, условия подобия девиаторов напряжений и деформаций, а также при введении параметров, являющихся функциями вида девиатора напряжений.

• 2.    Применение подобного уравнения, построенного на основании результатов статистических испытаний, к режиму циклического нагружения дает несколько заниженное значение расчетных деформаций ползучести. Предложена эмпирическая поправка к уравнению механических состояний.

• 3.    Уравнение механических состояний допускает учет функциональных параметров, зависящих от времени старения и меры поврежденности при длительном нагружении.