Помехоустойчивость некогерентного и когерентного приема ДФРМ-сигнала в условиях воздействия фазоманипулированной, гармонической или гауссовской помех
Автор: Ложкин К.Ю., Стиценко А.И.
Журнал: Журнал Сибирского федерального университета. Серия: Техника и технологии @technologies-sfu
Статья в выпуске: 2 т.10, 2017 года.
Бесплатный доступ
Методом индикаторов решений о переданных элементах получены зависимости средних вероятностей правильного приема в оптимальном некогерентном приемно-решающем устройстве символа и двоичного элемента простого незамирающего сигнала с двукратной фазоразностной манипуляцией при воздействии фазоманипулированной или гармонической помех от отношения сигнал-помеха. Проведен анализ указанных зависимостей и выполнено сравнение помехоустойчивости оптимального некогерентного и когерентного приемно-решающих устройств сигналов с двукратной фазоразностной манипуляцией при воздействии фазоманипулированной, гармонической и гауссовской помех.
Сигнал с двукратной фазоразностной манипуляцией, оптимальное некогерентное приемно-решающее устройство, фазоманипулированная, гармоническая, гауассовская помехи, вероятностностные показатели достоверности приема сигнала
Короткий адрес: https://sciup.org/146115197
IDR: 146115197 | DOI: 10.17516/1999-494X-2017-10-2-260-270
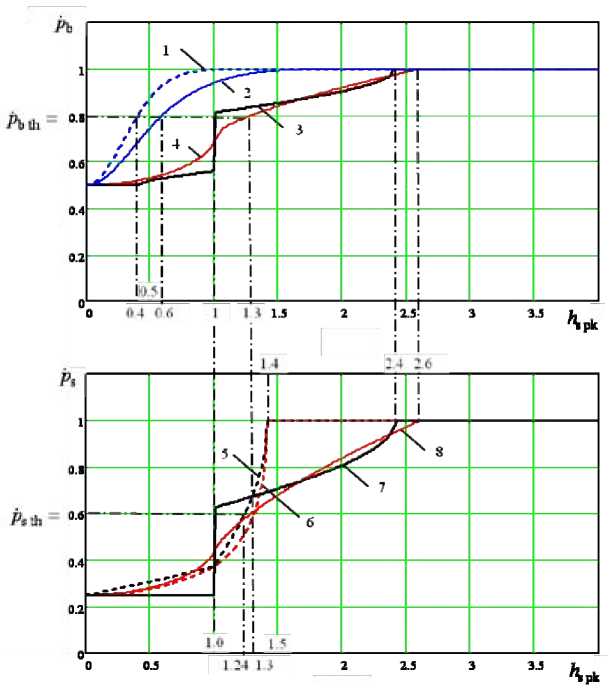
Список литературы Помехоустойчивость некогерентного и когерентного приема ДФРМ-сигнала в условиях воздействия фазоманипулированной, гармонической или гауссовской помех
- Окунев Ю.Б. Цифровая передача информации фазомодулированными сигналами. М.: Радио и связь, 1991. 296 с
- Зюко А.Г., Фалько А.И., Панфилов И.П., Банкет В.Л., Иващенко П.В. Помехоустойчивость и эффективность систем передачи информации. М.: Радио и связь, 1985. 272 с
- Гиршов В.С. Помехоустойчивость когерентного приема многопозиционных сигналов с фазоразностной модуляцией. Радиотехника, 1988, 1, 47-49
- Ложкин К.Ю., Поддубный В.Н. Достоверность когерентного приема простых ДФРМ сигналов на фоне помехи произвольной структуры. Радиотехника, 1999, 12, 34-38
- Loeve M. Probability Theory. Princeton, New Jersey, USA: D Van Nostrand, 1955. 685 p
- Овчаренко Л.А., Поддубный В.Н. Определение вероятности искажения последовательности двоичных сигналов методом индикаторов решений о переданных элементах. Известия вузов СССР. Серия Радиоэлектроника, 1986, 29 (9), 12-18
- Яглом А.М., Яглом И.М. Вероятность и информация. М.: Наука, 1975. 511 с
