Поочередное преследование с тремя участниками (случай поточечной встречи)

Решению простейшей дифференциальной игры поочередного преследования коалиции двух убегающих игроков посвящены работы [1; 3–7]. В нашей статье исследуется игра на плоскости преследователя Р и двух убегающих – E₁ и E₂ . Рассмотрим границу зоны безопасности второго из преследуемых игроков.

Отметим, что убегающие игроки действуют согласованно, т. е. составляют коалицию E = {E₁, E₂} . Выигрыш игрока E определяется как время встречи P с последним из убегающих игроков, выигрыш P – как величина выигрыша E с обратным знаком. Под встречей подразумевается совпадение местоположений игроков P и E_i (здесь и далее: i = 1,2).

Предположим, что в каждый момент времени преследователь P имеет информацию о своем местоположении, а также местоположении и направлении скорости игрока E_i . Игрок E , в свою очередь, имеет информацию о своем местоположении и местоположении игрока P .

Пусть u – линейная скорость игрока P, vi – линейная скорость убегающего Ei, u > vi. Будем полагать, что игроки движутся с максимальными скоростями и для простоты считать, что u = 1, v1 < 1, v2 < 1. Решение игры строится в предположении, что преследователь P в момент времени t = 0 выбирает один из следующих способов поведения [1; 6; 8]:

• 1)    использует правило параллельного сближения ( П -стратегия), преследуя сначала E₁ , затем E₂ ;

• 2)    использует правило параллельного сближения ( П -стратегия), преследуя сначала E₂ , затем E₁ .

Среди данных предположений найдем наилучший ответ убегающей коалиции E , который подразумевает максимизацию времени преследования.

Предположим, что в момент времени t = 0 игрок P принимает решение преследовать сначала E₁ , а затем E₂ .

Введем систему координат xOy , центр которой совпадает с начальным положением преследователя P , а ось абсцисс ориентирована в направлении начального положения игрока E₁ . Координаты точки P – P⁰ (0; 0), точки E₁ – E ₁ ⁰ ( b ; 0), точки E₂ – E ₂⁰ ( c ; d ) (верхними индексами будем отмечать положения игроков в соответствующие моменты времени). Границей зоны безопасности игрока E₁ является окружность Аполлония ( C₁ ) с радиусом r₁ и центром в точке ( a ; 0) [7–8; 10]:

v 1

r i = i---- 2 b ; a = i---- 2 b .

1 - V 1             1 - V 1

Обозначим точку встречи игроков P и E₁ : P^{t 1} ( x₁ ; y₁ ). Координаты x₁ , y₁ определяются соотношениями:

x 1 = a + r 1 cos а ; у 1 = r 1 sin а . (2)

За время t1 (момент встречи P и E1) игрок E2 может попасть в любую точ- ку круга с центром в точке E2 и следующим радиусом:

x i ⁺ У 1 .       (3)

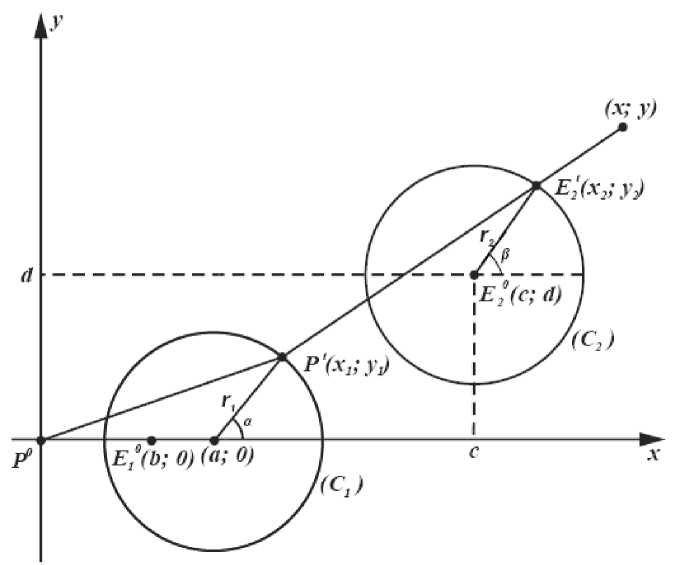
Р и с. 1. Построение границы зоны безопасности игрока E₂

F i g. 1. Building a border security zone E₂ player

Зафиксируем E₂ в точке E ₂ ^t ( x₂ ; y₂ ) окружности ( C₂ ). Координаты x₂ и y₂ определяются по формулам:

x 2 = c + r ₂cos в; y 2 = d + r ₂ sin Д ;

x 2 = c + r ₂cos в,          (4)

ф ( а , в ) = V ( x - a — r 1 cos a )² + ( y - r 1 sin a )² -

( x - c - r ₂ cos в )² + ( У — d — r ₂ sin в ) 2

-

V 2

.

где 0 <  в <  2 п , в = const .

Граница зоны безопасности игрока E₂ для начальных местоположений P^t , E ₂ ^t – окружность Аполлония:

Пусть точка E ₂ ^t «пробегает»

всю

окружность (C 2 ), т е. 0 <  в <  2 п . Найдем

U Ф ( а , р ) , т е. огибающую семейства (5). 0 < в < 2 п

7 ^( x — c — r₂ cos в ) ² + ( y — d — r ₂ sin в ) ²

—

9ф ( ^a , ^в ) = ( дв

— c —

v ₂

^cos в ) ^sin в — ( У — d — r ^ sin в ) ^cos в  о

= 0,

v ₂

Для этого рассмотрим следующую систему [3; 9]:

Из второго уравнения системы (6) следует:

Таким образом,

( x - c - r₂ cos в ) r ₂ sin в -

- ( y - d - r ₂sin в ) r ₂cos в = 0 ,

sin в =

y-d

cos в =

V (x - c )2 +(y - d )2 x - c

или

V ( x - ^c ) 2 + ( y - ^d ) 2

( x - c - r ₂ cos в ) r ₂ sin в = = ( y - d - r ₂ sin в ) r ₂ cos в .

Подставив равенства (7) в первое уравнение системы (6) и преобразовав полученное выражение получим:

x - c -

x - c

к

V( x ^{- c} ) 2 ⁺( y - ^d ) 2 ,

1 л

+ У - d - r2 к

v ₂

У - d

V

V ( ^x - ^c ) 2 ⁺( y - ^d ) 2 у

—

или

_ V( ^x - ^c ) ^{2 +}( y - ^d ) ²

v ₂

^^^^^^B

Ф ( a ) = ( x — a — r 1 cos a ) ² + ( y — r 1 sin a ) ²

x — c )2

v ₂

—

—

r 1 sm a ) ² = 0

x - a ) ² + y² + r i^ - 2 ( x - a ) r 1 cos a - 2 yr 1 sin a -

^ (x — c )2 +(У — d )2

^^^^^^B

v ₂

Г + 2 ar₁ cos a

= 0.

Таким образом, при

У ( x - c ) ² + ( У - d ) ²

v ₂

> а а ² + r 1 ² + 2 ar 1 cos а

ф ( а ) = У( x - а ) ² + у ² + г² - 2 r 1 [ ( x - а ) cos а + у sin а ]

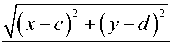
v ₂

+

+д/ а2 + г2 + 2ar1 cos а = 0, а при

( x - с ) 2 + ( у - d ) 2

v ₂

а2 + г2 + 2ar1 cos а x — a)2 + у2 + г2 — 2r1 [(x — a) cos а + у sin a J +

У ( x — с )2 +( у — d )2

—

v ₂

■ a ² + r² + 2 ar1 cos a = 0.

Пусть теперь точка P «пробегает» всю окружность Аполлония (С₁) , т. е. 0 <  а <  2 п . Найдем ^ Ф ( ^а ) , 0 < а < 2 п

т. е. огибающую семейства (8). Путем преобразований, аналогичным рассмотренным выше, получим систему:

Ф ( a ) = У( x - a ) ² + у ² + г² - 2 r 1 [ ( x - a ) cos а + у sin a J

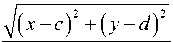
v ₂

a ² + r² + 2 ar 1 cos a

= 0,

dф(a) 1               (x - a) sin a - у cos a da r   У(x - a )2 + у2 + r12 - 2r1 [(x - a) cos a + у sin a J a • sign

^(x-c)2 +(у -d)2

v ₂

a ² + r 1 ² + 2 ar 1 cos a

sin a

a ² + r 1 ² + 2 ar 1 cos a

= 0.

Перепишем ее в следующем виде:

Rr - 1 ^ | = o,

( ( x - a ) sin a -

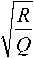
= 0,

где

R = ( x - a ) 2 + y ² + r 1 ² - 2 r 1 [ ( x - a ) cos a + y sin a J ; Q = 1 + v 2 + 2 v 1 cos a ;

M =

( x - c ) ² + ( y - d ) ²

-

v ₂

Стремление избавиться от радикалов путем возведения в квадрат приводит к громоздкой системе уравнений четвертой степени, решение которой допустимо только численно с последующей непростой процедурой отсеивания сопутствующих корней, поэтому подобный метод в данном случае бесперспективен.

Задача может быть решена напрямую с помощью средств компьютерной алгебры (например, как в данной статье, системой «Wolfram Mathematica»). Стратегия коалиции E состоит в выборе того, под каким углом будет убегать игрок E₁ . Очевидно, что после этого выбора определяется точка и время встречи игроков P и E₁ . В этом

aQ .

случае оптимальной стратегией игрока E₂ является удаление от этой точки с максимальной скоростью по прямой линии.

Построение границ зон безопасности было проведено с использованием функции «Parametric Plot», нахождение оптимального угла – с помощью «Maximize».

На рис. 2–10 представлены границы зон безопасности игроков E₁ и E₂ . На рис. 2 показаны направления движений игроков для обеспечения максимизации времени поимки E . На остальных рисунках направления движения игроков отличаются от оптимальных. Для примера были выбраны v₁ = 0,6; v₂ = 0,4.

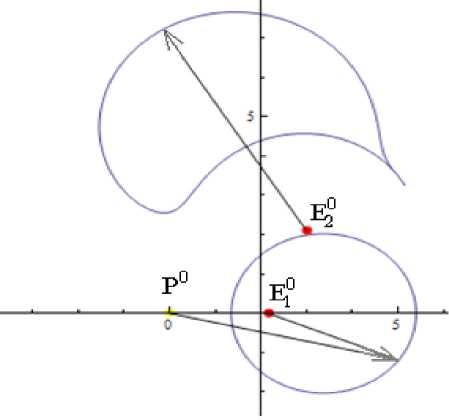
Р и с. 2. Расположение игрока E ₂ ⁰ вблизи окружности Аполлония (вне окружности)

F i g. 2. The player E ₂ ⁰ position near the circle of Apollonius (out of the circle)

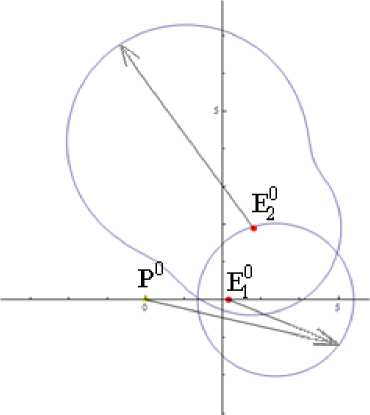
Р и с. 3. Расположение игрока E₂ ⁰ вблизи окружности Аполлония (внутри окружности)

F i g. 3. The player E₂ ⁰ position near the circle of Apollonius (inside the circle)

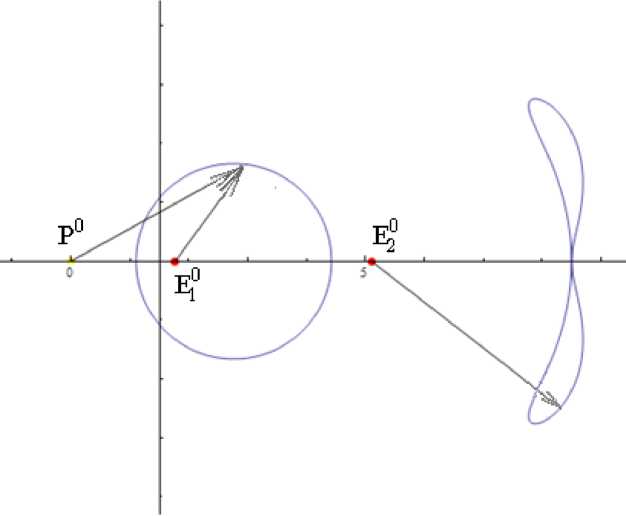
Р и с. 4. Расположение P ⁰ , E₁ ⁰ , E₂ ⁰ на одной прямой ( E₂ ⁰ – вне окружности Аполлония)

F i g. 4. P ⁰ , E₁ ⁰ , E₂ ⁰ are located on the same line, E₂ ⁰ is situated out of the circle of Apollonius

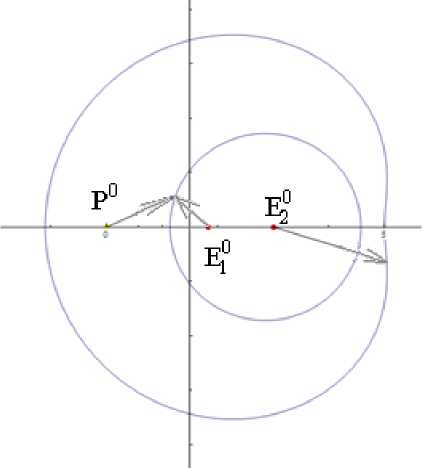
Р и с. 5. Расположение P ⁰ , E₂ ⁰ , E₂ ⁰ на одной прямой ( E₂ ⁰ – внутри окружности Аполлония)

F i g. 5. P ⁰ , E₁ ⁰ , E₂ ⁰ are located on the same line, E₂ ⁰ is situated inside the circle of Apollonius

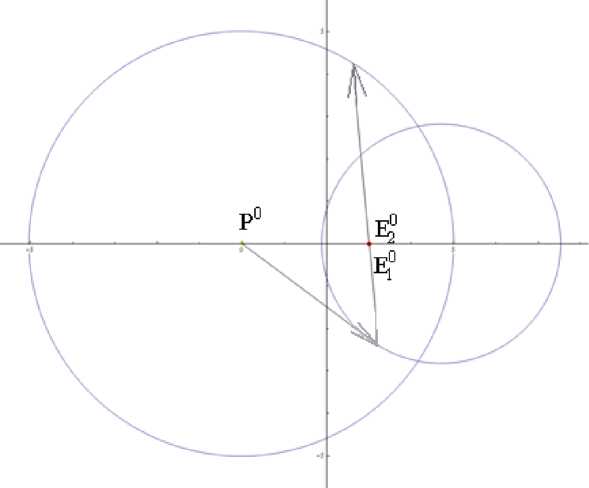
Р и с. 6. Начальные местоположения E₁ ⁰ = E₂ ⁰

F i g. 6. Initial location E₁ ⁰ = E₂ ⁰

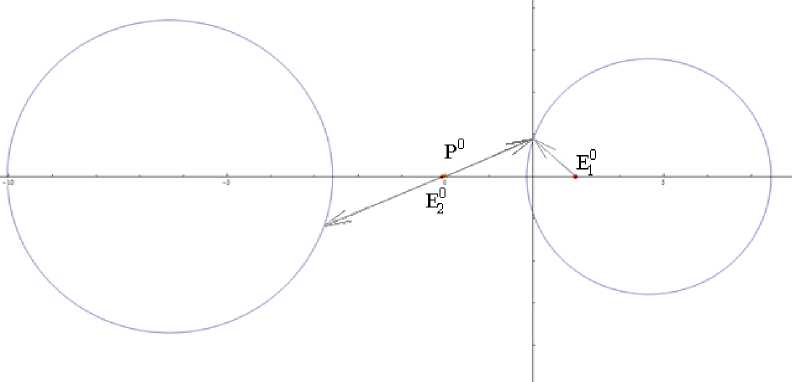
Р и с. 7. Расположение P ⁰ , E₁ ⁰ , E₂ ⁰ на одной прямой ( E₂ ⁰ – вблизи P ⁰ )

F i g. 7. P ⁰ , E₁ ⁰ , E₂ ⁰ are located on the same line, E₂ ⁰ is situated near P ⁰

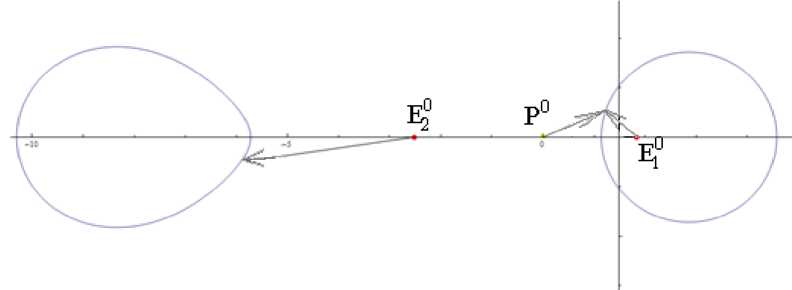
Р и с. 8. Расположение P ⁰ , E₁ ⁰ , E₂ ⁰ на одной прямой ( P ⁰ – между E₁ ⁰ и E₂ ⁰ )

F i g. 8. P ⁰ , E₁ ⁰ , E₂ ⁰ are located on the same line, P ⁰ is situated between E₁ ⁰ and E₂ ⁰

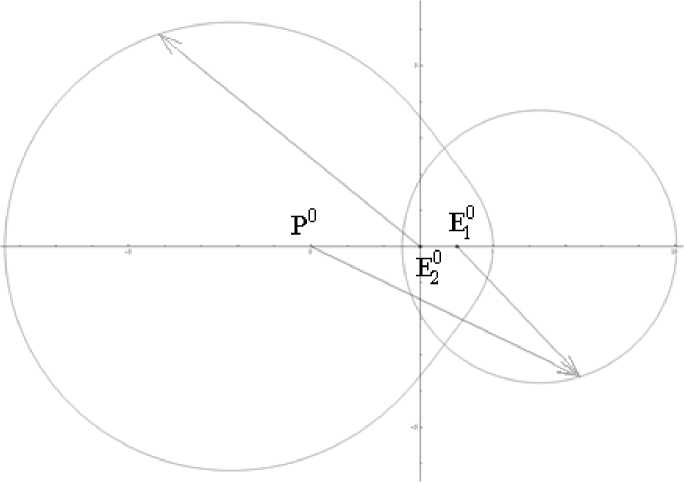
Р и с. 9. Расположение P ⁰ , E₁ ⁰ , E₂ ⁰ на одной прямой ( E₂ ⁰ – между E₁ ⁰ и P ⁰ внутри окружности Аполлония)

F i g. 9. P ⁰ , E₁ ⁰ , E₂ ⁰ are located on the same line, E₂ ⁰ is situated between E₁ ⁰ and P ⁰ inside the circle of Apollonius

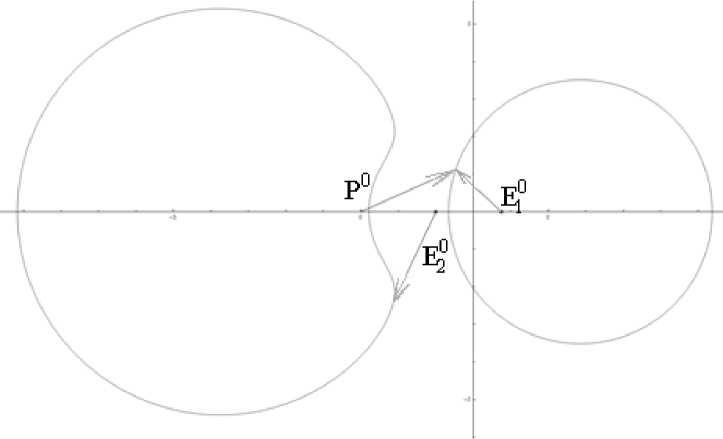
Р и с. 10. Расположение P ⁰ , E₁ ⁰ , E₂ ⁰ на одной прямой ( E₂ ⁰ – между E₁ ⁰ и P ⁰ за окружностью Аполлония)

F i g. 10. P ⁰ , E₁ ⁰ , E₂ ⁰ are located on the same line, E₂ ⁰ is situated between E₁ ⁰ and P ⁰ out of the circle of Apollonius

На рис. 2–3 точка E ₂ ⁰ расположена достаточно близко к границе зоны безопасности игрока E ₁ ⁰ , поэтому часть границы зоны безопасности игрока E ₂ ⁰ близка к окружности. Причиной этого является то, что местоположение E ₂ ⁰ на границе зоны безопасности представляет собой точку разрыва, поскольку при выборе направления E₁ к E₂ направление движения игрока E₂ однозначно выбрать невозможно.

Определив границу зоны безопасности второго из убегающих игроков,

можно аналогично рассмотренному исследовать игру между преследователем P и тремя преследуемыми E₁ , E₂ , E₃ [2], действующими согласованно (фактически исключив из игры первого из преследуемых игроков). Кроме того, предложенный метод может быть использован при решении простейшей дифференциальной игры поочередного преследования коалиции двух убегающих игроков в случае R-встречи (R > 0) с первым игроком и поточечной встречи – со вторым.

Поступила 23.10.2015 г.

Submitted 23.10.2015

About the authors:

Physics and Mathematics 31