Поперечная жесткость круглых лесоматериалов: эксперименты и численное моделирование

Постановка задачи. Жесткость определяется в механике как способность упругого тела сопротивляться появлению деформаций (растяжения, сжатия, изгиба, сдвига, кручения) [11]. Представляет интерес зависимость жесткости баланса от величины его диаметра, от модулей упругости коры и древесины, возраста, влажности и других физико-математических характеристик. Мерой жесткости служит отношение силы к той деформации, которая вызывается ее действием. При малых деформациях (в пределах закона Гука) эта зависимость линейна.

В математической модели соударений балансов в процессе их очистки в корообдирочном барабане используется понятие «жесткость при сжатии». Под этим понимается коэффициент пропорциональности между силой, действующей на баланс, и соответствующим ей линейным перемещением. Более того, поскольку соударения балансов сопровождаются образованием так называемого пятна контакта, указанная жесткость может приводиться к единице его длины и иметь размерность (H/м)/м) = H/м2. В дальнейшем изложении следует различать жесткость баланса и его погонную жесткость, то есть жесткость, отнесенную к единице длины.

При моделировании соударений балансов в процессе их очистки в корообдирочном барабане необходимо принимать во внимание, что кора и остальная часть баланса существенно различаются по жесткости. Различия в жесткости материалов характеризуются модулями упругости, которые определяются экспериментально. Наи

более детально исследованы механические свойства древесины [1], [5], [9]. Менее детально исследованы механические свойства коры [2]. В еще меньшей степени изучены вопросы, связанные с определением жесткости баланса как системы, образованной совместно деформируемыми корой и остальными частями древесного ствола.

Экспериментальное определение жесткости еловых балансов. В качестве объекта экспериментального исследования выбраны еловые балансы. Образцы естественной влажности в виде отрезков бревен длиной 1 м были заготовлены в октябре 2008 года на одном из предприятий лесопромышленного комплекса в деревне Шок-ша Вепской национальной волости Республики Карелия. Испытания выполнены в октябре 2008 года на машине Р-10 с приложением нагрузки в радиальном направлении (рис. 2).

Зависимость сближения точек A и B от величины силы P (рис. 1) отображалась на диаграмме (рис. 2).

Образцы не доводились до разрушения, испытания проводились в условно упругой стадии, что подтверждалось почти прямо пропорциональной зависимостью сближения точек A и B от силы P .

В процессе испытаний положение образца изменялось его поворотом на 900 вокруг продольной оси и цикл указанных выше измерений повторялся. Было найдено, что сила, вызывающая сближение точек A и B (рис. 1) на 1 мм, равна 1360 Н для баланса диаметром 14,6 см, число годовых колец которого равно 81. Для баланса диа- метром 23 см с числом годовых колец 147 значение этой силы возросло до 5000 Н, что является закономерным, поскольку жесткость материала древесного ствола с возрастом увеличивается.

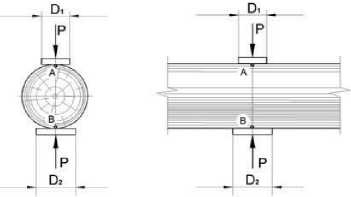
Рис. 1. Схема испытаний

Рис. 2. Общий вид установки для испытаний

Интерпретация результатов измерений. Для интерпретации результатов измерений воспользуемся упрощенной схемой (рис. 3).

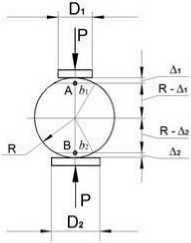
Рис. 3. К интерпретации результатов измерений

Аналогичные схемы применяются в исследованиях контактного взаимодействия цилиндрических тел методами теории упругости [10]. Из схемы на рис. 3 следует, что

A i = R - V R ² - b ². (1)

Преобразуем выражение (1) к виду:

^A = 1 - V1 - ( b i/ R ) ² .

R

Тогда 1- (b1/R )2 =1+(A1/R )2 - 2(A,ZR),(3)

(b1/R )2 =2(A,ZR) - (A,ZR )2.(4)

По физическому смыслу задачи можно считать, что A 1 <<  R , то есть A 1 / R << 1. Пренебрегая в (4) величиной ( A 1 /R )², получаем:

b2 = 2 A. R(5)

11 .

Аналогично, используя ту же схему (рис. 3), запишем:

b22 = 2A 2 R.(6)

Величинами b 1 и b ₂ приближенно определяется ширина области контакта, которая определяется методами теории упругости [10].

Если воспользоваться упрощенной моделью баланса, рассматривая его как однородный цилиндр из изотропного материала с модулем упругости E и коэффициентом Пуассона ц = 0,3, то для контакта цилиндра с плоской поверхностью величина b 1 будет равна [10]:

^ь 1 - 1.52 . (7)

Здесь P1 - нагрузка на единицу длины поверхности контакта. В нашем случае (рис. 3) нагрузка на баланс передавалась через жесткие диски диаметром D 1 и D2. Принимая во внимание, что b 1 << D 1, определим площадь контакта как площадь узкого прямоугольника шириной 2b 1 и длиной D 1. Тогда нагрузка на единицу длины контакта

P = D

.

Аналогично b2 - 1-52 IPER -

P = P ² D 2 .

Исключая b 1 из равенств (5) и (7), найдем:

А , = 1,16 p .                   (11)

E

Аналогично, подставив (9) в (6), найдем:

А₂ = 1,16 P .                 (12)

² E

Соотношения (11) и (12) позволяют сделать важный в практическом отношении вывод: при моделировании соударений балансов в корообдирочном барабане влиянием поперечных размеров баланса можно пренебречь, если материал всех балансов имеет один и тот же модуль упругости E . Однако необходимы уточнения, обусловленные влиянием возраста древесины, а значит, и диаметра, на модуль упругости E .

С применением (11) и (12) найдено, что сила 1360 Н вызывает сближение точек A и B (рис. 1) на величину A = 1 мм, что означает:

A = A 1 + A 2 .                  (13)

Величины A и A 2 прямо пропорциональны величинам P 1 и P 2 :

A 1 ZA 2 = P 1 / P 2 .                (14)

Учитывая (8) и (10), запишем:

A/A = D 2 / D 1 .

Поскольку Δ2 = Δ – Δ1, преобразуем отношение (15):

Δ₁( D ₁+ D ₂) = D ₂Δ.             (16)

Δ₁= D ₂Δ/( D ₁+ D ₂).             (17)

В рассматриваемых случаях D ₁ = 9,5 см, D ₂ = 14, 5 см, Δ = 0,1 см. Тогда:

Если, например, E_r = (67000 ± 1340) Н/см ², то по формуле (26) нижняя оценка погонной жесткости:

s 1 = s 2 = 0,041 • 53600 = 2200 Нсм . (27) см

Δ1= 14,5 ∙ 0,1/(9,5 + 14,5) = 0,0604 ≈ 0,6 мм, Δ2 = 0,1 – 0,0604 ≈ 0,4 мм.

Верхняя оценка:

S 1 = S ₂ = 0,041 • 80400 = 3300 Нсм .    (28)

см

Представим баланс состоящим из двух полуцилиндров. По определению, погонная жесткость S ₁ верхней половины сечения баланса (рис. 3) равна:

S ₁ = S ₁ / D ₁ ^{. (18)}

Учитывая жесткость той же части S ₁ = P ₁/Δ₁,

получим:

S = —

¹ DA

0,0604 • 9,5

= 2370 НЦ. см ²

Аналогично

s, = -P

²    D ₂ A 2

0,0396 ^ 14,5

= 2370 ^— . см ²

Величины (19) и (20) получены для баланса диаметром 14,5 см. Испытания баланса диаметром 23 см по техническим условиям были выполнены на другой установке. Нагрузка на баланс передавалась через две одинаковые плиты длиной 28 см каждая. При этом было установлено, что сила 5000 Н вызывает сближение точек A и B на 1 мм. Это означает, что Δ1 = Δ2 = 0,5 мм,

S = s₂ = ⁵⁰⁰ = 3570 - Н- . (21) ^{1 2} 0,05 • 28 см ^{2 (} )

Определение жесткости баланса с применением методов теории упругости. Погонная жесткость определяется отношением силы к соответствующему этой силе перемещению:

S i = P , M ; S 2 = P 2 M .

Подставив (11) и (12) в (22), получим:

S = s ₂ = 0,86 E.

Здесь E – приведенный (или усредненный) модуль упругости:

Для перехода от погонной жесткости к обычно используемой в расчетах необходимо величину S₁ (28) или (27) умножить на длину пятна контакта.

С учетом вариабельности свойств свежеза-готовленной древесины можно сделать вывод о том, что полученные с применением методов теории упругости оценки (27) и (28) достаточно хорошо согласуются с результатами эксперимента (19), (20), (21).

Результаты определения жесткости балансов с использованием программы конечноэлементного анализа. Воспользуемся программой конечно-элементного анализа «Лира-9». С точки зрения механики рассматриваемая проблема формулируется как плоская задача теории упругости, для решения которой применяется метод конечных элементов. Баланс упрощенно рассматриваем как однородное изотропное тело, модуль упругости материала E , коэффициент Пуассона μ = 0,3 .

Для определения закономерностей влияния модуля упругости материала и диаметра баланса на его жесткость была выполнена серия расчетов, результаты которых представлены в таблице.

В таблице приведены значения силы, вызывающей сближение точек A и B на 1 см для условного баланса при D ₁ = D ₂ (рис. 1). Расчеты выполнены с использованием модели, в которой число конечных элементов равно 4455, число узлов – 2323, число уравнений метода конечных элементов – 4628.

Результаты, полученные по программе «Лира-9»

E = E ₀ E _r /( E ₀ + E _r).            (24)

Здесь E ₀ и E_r – модуль упругости соответственно коры и древесины при сжатии в радиальном направлении. Методика измерения и характеристики жесткости коры исследованы А. С. Васильевым [2]. С учетом известных по литературе данных [5] можно приближенно считать, что для еловых балансов E r = 0,67 ГПа (67000 - Н 2- ), E ₀ = E r /20 .

Модуль упругости материала (Н/см2)	Диаметр баланса (см)
	15	20	25	30
2500	576	576	576	576
50000	1152	1152	1152	1152
75000	1728	1728	1728	1728
100000	2304	2304	2304	2304

Полученные результаты численного моделирования (см. таблицу) подтверждают правомерность вывода о том, что диаметр баланса не влияет на величину его деформации в рассматриваемой задаче.

Тогда

E =     E r * E r

см

E r

20( E r /20 + E r )   21.

S 1 = S 2 =

P 1

A ,

1152 = 2304^2 .

0,5 см ²

Подставив (25) в (23), получим:

S ₁ = S ₂ = 0,86 ∙ E_r /21 = 0,041 E_r .       (26)

Результаты расчета (см. таблицу) показывают, что округленные до целых значения силы,

вызывающей сближение точек A и B на 1 см, не зависят от диаметра цилиндра. Эти данные позволяют записать следующую эмпирическую зависимость:

S ₁ = S ₂ = 0,046 E .            (29)

Зависимость (29) аналогична ранее полученной зависимости (26), что подтверждает достоверность результатов исследования. Расхождение коэффициентов в (26) и (29) составляет:

е = ^0,046 - ^0,041 • 100 % = 12 %        (30)

0,041                     ^.

Используя результаты расчета (см. таблицу), вычислим нижнюю и верхнюю оценки жесткости баланса с указанным выше модулем упругости E = E_r = (53600...80400) H/см ². По формуле (29) вычисляем верхнюю оценку:

S ₁= S ₂ = 0,046 ∙ 80400 = 3700 ( Н/см )/ см . (31)

По той же формуле определяем нижнюю оценку:

S ₁ = S ₂ = 0,046 ∙ 53600 = 24700 ( Н/см) / см . (32)

Перемещение Δ1 (рис. 4) представим в виде суммы:

Δ1= Δ0 +Δw,                 (33)

где величина Δ₀ обусловлена деформированием коры, а величина Δ _w определяет свойства древесины.

Как указано выше, жесткость

S ₁ = P ₁/ Δ ₁.                    (34)

Аналогично

S ₀ = P ₁/ Δ ₀; S_w = P ₁/ Δ_w .             (35)

Тогда

Δ ₀ = P ₁/ S ₀; Δ_w = P ₁/ S_w . (36) С учетом (33) получаем:

S 1 = S 0 S w / ( S 0 + S w ). (37)

Принимая во внимание, что согласно равенству (23) указанные в формуле (37) жесткости прямо пропорциональны соответствующим модулям упругости, приходим к равенству (24).

ВЫВОДЫ

• 1.    Разработана методика определения жесткости балансов с корой при сжатии в радиальном направлении. Результаты экспериментального и численного определения жесткости балансов согласуются с данными, полученными по формулам теории упругости.

• 2.    Влияние величины только диаметра баланса на его жесткость пренебрежимо мало. Однако диаметр баланса зависит от возраста древесины, а с возрастом изменяется жесткость коры и основной части древесного ствола. Поэтому жесткость баланса оказывается зависящей от возраста. Установлено, что жесткость баланса прямо пропорциональна модулю упругости, но не равна ему (23).

• 3.    Результаты определения жесткости по разработанной методике используются в качестве исходных данных при численном моделировании соударений балансов в процессе их очистки от коры в установках барабанного типа [3], [4], [7], [8], [11]. Кроме того, эта же методика может быть использована для получения исходных данных в расчетах деформаций при проектировании новых и обследовании существующих строений из круглых лесоматериалов.

* Работа выполнена при поддержке Программы стратегического развития (ПСР) ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012–2016 гг.