Поправка для расчета интенсивности рефлексов при малоугловом рентгеновском исследовании плоских микро и наноэлементов при разных углах наклона

Микроэлектронные компоненты, функцииональные элементы наноуровня начинают широко проникать в сферу бытовых устройств, регулярно используемых в повседневной жизни. Для (сервисного обслуживания) обслуживания, диагностики, создания таких элементов необходимым условием является контроль качества и анализ структуры, поскольку структура определяет свойства. Такие элементы могут представлять собой маленькие (миллиметрового размера) плоские образцы, часто имеющие слоевую структуру.

Одним из методов исследования слоевых плоских электронных и других компонентов современной техники является метод малоуглового рентгеновского рассеяния. Анализ структуры может, например, проводится с помощью расчёта структурного фактора элемента кристаллической структуры, который умножается на интерференционную функцию и далее сравнивается с экспериментом [1]. Для такого анализа необходимо знать истинные значения интенсивности рентгеновского рассеяния. При расшифровке рентгеновской картины вносят поправки - поляризационный множитель интенсивности и множитель Лоренца, учитывающий мозаичность образца.

В качестве примера, можно использовать нанесённую на монокристаллическую пла- стинку кремния мультислоевую плёнку на основе мезогенных молекул.

При рентгеновском исследовании нанослоёв из мезогенных молекул на плоских подложках кремния дифракционная картина в зависимости от угла наклона подложки может сильно изменяться. При малых углах наклона подложки условию дифракции Лауэ, удовлетворяют рефлексы с большим периодом. Дальнейший поворот образца приводит к перераспределению интенсивности, и на дифракционной картине начинают возникать рефлексы следующих порядков. Однако, если сечение коллиматора больше сечения подложки, то при повороте на больший угол интенсивность, падающего на образец излучения увеличивается.

На рис.1. показано, что при наклоне подложки к оси коллиматора под углом α 1 , в образовании дифракционной картины участвуют лучи выходящие из СС’D’D. При увеличении наклона образца на α 2 >α 1 , перекрываемая площадь увеличивается до ABB’A’, а, следовательно, увеличивается интенсивность и дифрагированных лучей.

Для внесения поправки в интенсивность рефлексов, полученных при разных углах наклона образца, рассмотрим рис.2.

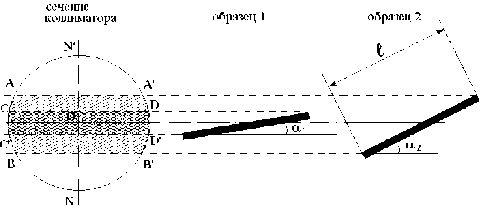
Рисунок1. Геометрия рентгеновского эксперимента α 2 >α 1

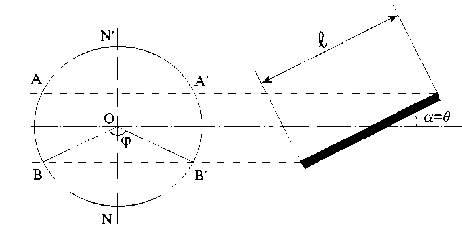
Рисунок 2. К расчету поправки в интенсивность рефлексов

В формировании дифракционной картины участвуют лучи, перекрываемые площадью АА’B’B. Оценим ее.

S AA'B'B = S круга - 2 S BBN = ^ R 2 - R ²( ф - ^П ф );

S AA'B'B ^{R ( П ф +} sin ^ ) ;

ф = 2arccos ( h /2 R ) ; h=AB ;

(I • sinaA ф = 2arccos ;

I 2 • R )

интенсивность пика в зависимости образца

от наклона

I

ист

S 0 =

I эксп ист

S (a)

При увеличении угла наклона образца с угла α 0 на угол α 1 интенсивность падающего пучка на образец увеличивается пропорционально увеличению перекрываемой образцом площади с S 0 (α) которой соответствует, например, фигура CC’D’D до площади S 0 +Δ S (α 1 ), которую занимает AA’B’B. Исходя из этого, истинное значение интенсивности для разного угла наклона плоского образца будет

I ист

I ист

= I эксп ( « 0 ) _;

S 0 ;

= I эксп ^{( a} 0 ⁺ « 1 ) S 0 + A S ( a 1 ) ,

а решением этой системы относительно S 0 и I ист

есть

I эксп ^{( a} 0 ^+a i ) ^- I эксп ^{( a} 0 ) _;

Δ S (α₁)

I эксп ( a o ) • a S ( a 1 )

I эксп ^{( a} 0 ^+a i ) ^- I эксп ^{( a} 0^).

Но если принять при I = I max , α=α 0 =θ, а

α 1 новый угол, что S 0 = S (α 0 ), S 1 = S (α 1 ) и

I ист = I 0 / S 0 = I 1 / S 1 , то

1 0 = 1 1 • ( S 0 / S i ) .                 (8)

Исправленное значение интенсивно-

сти дифракционных максимумов позволяет бо-

лее качественно проводить моделирование мультислоевой структуры используя, наклон молекул и их перекрытия [2]. График изменения площади коллиматора, перекрываемой образцом с плёнкой, представлен на рис.3.

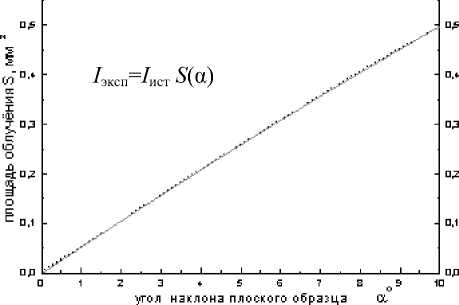
Рисунок 3. Зависимость площади перекрывания коллиматора с D =1 мм от угла наклона (до 10°) мультислоевой ЖК структуры на 3 мм кремниевой подложке

Эту кривую можно с точностью до 0.1% для углов 0<α<10° интерполировать квадратным полиномом, учитывая периоды слоёв от 5Å и больше

S (α)= A + B 1 α+ B 2 α² (9) где: A =-0,00145; B 1 =0,05404; B 2 =-0,00041112