Порядок извлечения ресурсов с различными издержками добычи в условиях наличия неопределенности в будущем спросе
Автор: Беломестный Д. В., Орлова Т. С., Полбин А. В.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Информатика и управление
Статья в выпуске: 2 (58) т.15, 2023 года.
Бесплатный доступ
В работе предлагается динамическая стохастическая модель общего равновесия с двумя исчерпаемыми источниками энергии (ресурсами): с низкими издержками добычи (нефть) и высокими (уголь). При этом будущий спрос на данные ресурсы является стохастическим, что в модели реализуется за счет стохастического улучшения в технологии производства альтернативных источников энергии. На основе численного имитационного анализа показывается, что если в детерминированной и стохастической задачах центрального планирования оптимальным является последовательное извлечение природных ресурсов, когда первым извлекается ресурс с низкими издержками добычи, то в модели рыночного равновесия с несколькими экономическими агентами, гетерогенными относительно прав собственности на природный ресурс и не разделяющими между собой риски, на рынке одновременно торгуются ресурсы с высокими и низкими издержками добычи.
Исчерпаемые ресурсы, динамическая стохастическая модель общего равновесия, неопределенность в будущем спросе, стохастическое улучшение в технологии производства, нефть, уголь, гетерогенные агенты, неполные рынки
Короткий адрес: https://sciup.org/142238151
IDR: 142238151 | УДК: 339.56.055
Текст научной статьи Порядок извлечения ресурсов с различными издержками добычи в условиях наличия неопределенности в будущем спросе
Классические модели оптимального извлечения невозобновляемого природного ресурса говорят нам о том, что чистая цена на ресурс (цена за вычетом издержек) должна увеличиваться во времени с темпом прироста, равным ставке процента [1], и оптимальной является последовательная разработка месторождений в порядке увеличения их издержек добычи [2], [3]. Данные выводы сохраняются как при рассмотрении задачи с репрезентативным домохозяйством, так и рыночной экономики, функционирующей в условиях совершенной конкуренции. Однако на практике данные закономерности не наблюдаются. В настоящей работе предлагается стохастическая модель общего равновесия, в которой анализируется один из факторов, почему может не выполняться второе теоретическое положение, а именно - на рынке одновременно торгуются ресурсы с высокими и низкими издержками добычи. Мы рассматриваем экономику, в которой у каждого ресурса есть свой собственник и разделения риска между агентами не происходит. Соответственно, каждый экономический агент заботится о максимизации ожидаемых выгод от извлечения собственного ресурса, не принимая во внимание последствия своих действий для общего экономического благосостояния. В рассматриваемой постановке задачи предполагается, что с некоторой вероятностью в будущем спрос на ресурс с высокими издержками добычи может резко сократиться (что в модели реализуется за счет стохастического улучшения в технологии производства альтернативных источников энергии). Это побуждает собственника ресурса с высокими издержками добычи извлекать природный ресурс в текущие периоды времени одновременно с ненулевой добычей более дешевого ресурса.
Настоящая работа дополняет широкий пласт литературы, в котором разрабатываются альтернативные модели, объясняющие одновременную добычу нескольких ресурсов с разными издержками добычи. В работе [4] рассматривается модель с легкоизвлекаемыми и трудноизвлекаемыми природными ресурсами. Перед началом выработки второго ресурса необходимо понести издержки на установку капитала. Автором показывается, что в равновесии на отдельном интервале времени возможна одновременная добыча как легкоизвлекаемого, так и трудноизвлекаемого ресурса. На данном интервале времени добыча трудноизвлекаемого ресурса находится на максимуме производственных возможностей. В работе [5] показывается, что в модели с несколькими исчерпаемыми ресурсами с разными издержками добычи и неисчерпаемым ресурсом, но имеющим верхнее ограничение на объем производства, возможна ситуация, когда исчерпаемый ресурс с низкими издержками добычи сберегается для будущих периодов времени с целью сглаживания потребления, а первыми добываются исчерпаемые ресурсы с высокими издержками.
В работе [6] предлагается модель с гетерогенным спросом на различные источники энергии. Авторы предполагают, что нефть, ресурс с низкими издержками добычи, эффективна как при производстве электричества, так и при использовании в транспортном секторе. Уголь, ресурс с высокими издержками добычи, оказывается менее эффективным при использовании в транспортном секторе. В данных условиях оказывается оптимальным сохранить на будущие периоды времени часть нефти для использования в транспортном секторе. В решении специфицированной модели возникают три фазы добычи природных ресурсов. На первой фазе добывается только нефть, и она используется как для производства электричества, так и в транспортном секторе. На второй фазе нефть используется только в транспортном секторе, а уголь используется для производства электричества. На третьей фазе потребности в энергии в обоих секторах реализуются только за счет угля. В работе [7] рассматривается модель картельного поведения на мировом рынке нефти, когда один из игроков с низкими издержками добычи - ОПЕК, принимает решения о добыче, реализуя свою рыночную власть и принимая во внимание последствия от своих действий для цены на энергоресурс и для добычи конкурентов, а прочие же игроки с более высокими издержками добычи воспринимают цены как заданные. В данной модели реализуется равновесие с более высокой ценой на нефть и с одновременной добычей нефти игроков с разными издержками добычи.
Наиболее близким к настоящей работе является исследование [8], в котором также ключевая ролв в одновременном использовании нескольких исчерпаемых ресурсов отводится неопределенности. Авторы строят модель с двумя ресурсами, в которой издержки добычи одного из ресурсов являются стохастическими: они могут принимать низкие и высокие значения с некоторой вероятностью. В случае, когда в текущем стохастическом состоянии среды издержки добычи «безрискового» ресурса ниже издержек добычи «рискового» ресурса, но при этом существует вероятность, что в будущем издержки «рискового» ресурса окажутся еще выше, при определенных параметрах модели будет оптимальным добывать оба ресурса одновременно, чтобы сохранить часть дешевого «безрискового» ресурса на периоды времени, когда у добычи «рискового» актива увеличатся издержки. В детерминированном случае в текущем периоде времени добывался бы только дешевый «безрисковый» актив. В случае, когда в текущем стохастическом состоянии среды издержки добычи «безрискового» ресурса выше издержек добычи «рискового» ресурса, но при этом существует вероятность, что в будущем издержки «рискового» ресурса окажутся еще ниже, то здесь также при определенных параметрах модели может оказаться оптимальным добывать два ресурса одновременно. Но мотив уже заключается в сохранении «рискового» ресурса на периоды, когда он окажется еще дешевле.
Работа построена следующим образом: во втором разделе находятся описание, калибровка детерминированной модели центрального планирования, а также численный эксперимент. Третий раздел посвящен стохастической модели центрального планирования и включает ее описание, калибровку и численный эксперимент. Основная идея статьи находится в четвертом разделе, который посвящен международной стохастической модели общего равновесия.
2. Детерминированная модель центрального планирования2.1. Описание модели
В работе рассматривается задача центрального планирования, в рамках которой центральный планировщик максимизирует дисконтированный поток полезностей домохозяйств при ресурсных ограничениях. Прежде всего рассмотрим детали ограничений данной модели. Производство товаров и услуг конечного потребления Y в момент времени t в данном случае требует использования труда Ly,t, капитала Ky,t и энергии Et и будет осуществляться по технологии Кобба - Дугласа, а именно
Yt = АК^Д^^, (!)
, где A - уровень совокупной факторной производительности для производственного сектора, параметры а и /3 показывают доли капитала и труда в общем объеме затрат для данного сектора. Используемая в данном производственном уравнении энергия является комбинацией энергий трех видов: чистой энергии (альтернативные источники энергии, такие как: солнце, ветер, гидроэлектроэнергия) - St и энергий, получаемых при использовании углеводородов (углеводородных носителей), таких как нефть и природный газ - ot, а также уголь - ct. Таким образом, энергия, используемая для производственного сектора в момент времени t, может быть представлена в виде
Et = St + Ot + ct. (2)
В свою очередь, чистая энергия требует использования труда Ls,t, капитала Ks,t и земельных ресурсов Ht и осуществляется также по технологии Кобба - Дугласа:
St = ВК^Ң-^, (3)
где B - уровень совокупной факторной производительности для энергетического сектора, параметры Ө и ф показывают доли капитала и труда в общем объеме затрат для данного сектора. В рассматриваемой нами постановке задачи будем считать площадь используемых земельных ресурсов Ht постоянной величиной, т.е. Ht = Н.
Производство товаров и услуг конечного потребления у , в момент времени t используется для потребления, инвестиций, издержек на добычу углеводородов:
Yt = С- + Kt +1 - (1 - 5)Kt + XoOt + XcCt, (4)
где 6 Е (0,1) - норма амортизации капитала, Ct - потребление в момент времени t, а хс и ;уо затраты, связанные с добычей единицы угля, единицы нефти и природного газа соответственно. Будем считать данные затраты постоянной величиной для каждого вида углеводородного энергоносителя. Также необходимо отметить, что углеводороды являются исчерпаемым источником энергии и их запасы R , и R^ ограничены в каждый момент времени t > 0. При добыче и продаже углеводородов в периоде t в объемах ct и о , соответственно запасы углеводородов сокращаются и удовлетворяют следующим условиям:
Rt +1 = R? — Ot Rt +1 = rC — ct ot > 0, ct > 0, R t+1 > 0, R t+1 > 0.
Общие предложения капитала Kt и трудовых ресурсов (труда) Lt равны сумме их отраслевых составляющих через уравнения
Kt = K,t + Ks,t, Lt = Ly,t + Ls,t.
Далее рассмотрим нашу модель планирования с бесконечным горизонтом с точки зрения домохозяйств. Следуя работе [9], задачу оптимального управления мы формулируем в виде максимизации дисконтированного потока полезностей от потребления репрезентативного домохозяйства при ограничениях на ресурсы и потребление.
Домохозяйство стремится в каждый момент времени t увеличить суммарную полезность по всей траектории с учетом ставки временного предпочтения р, определяемую по формуле
∞
U = £ з=о
1 С + -1 (1 + р)3 1 - С
где с - коэффициент относительного неприятия риска. Если мы хотим ранжировать потоки потребления в соответствии с этой целевой функцией (7), мы должны убедиться, что сумма в правой части (7) ограничена сверху, т. е. Ut < то для любой допустимой последовательности точек Ct, С , +і , Ct +2 ,.. .• Это будет иметь место, если коэффициент роста однопериодной полезности с некоторого момента J
9 :=
/-ү 1 — ст с , + з +1
-
z-y 1 — ст
Ct + 3
-
< 1 + р
для всех i > J . Таким образом, задача оптимального управления состоит в максимизации
∞ max Ut = max 5
C t ,ct+ 1 ,... C t ,ct+ 1 ,...^
3 0
1—ст
1 ct + j
-1
(1 + р)3 1 -с
при условии
|
Kt +1 + Ct = Kt = Lt = |
АК"tL9tEt ' y,L y,L L Ky,t + Кй^, Ly,t + Ls,t, |
|
R°+1 = |
r(° - ot, |
|
RC+1 = |
RC - ct, |
|
Et = |
St + ot + ct, |
|
St = |
ВК8’tLp,H 1 - Ө - р o,L й,L L |
|
0 < |
R ° Rt +1 , |
|
0 < |
R C Rt +1 , |
|
0< |
ct, |
|
0< |
Ot, t = 0,1,... |
,
+ (1 - д)Kt - XoOt
-
XcCt,
Для решения задачи максимизации функции полезности (8) воспользуемся уравнением Беллмана, которое базируется на принципе оптимальности Беллмана.
Мы можем определить функцию полезности а рекурсивно через
а(К, R°, Rc ) = max ( ——-
' К‘,C,Ky,Ks,E,S} \ ‘ly,Ls,o,c,R°,RCj
Ro ,RC ,K 'R'° ,R,C )1 "
1 -a
-
-+
(Ю)
+^-а (К‘,R‘°,R'C ) J
1 + P при ограничениях (9), где переменные с ’ обозначают переменные следующего периода, а без ’ - текущего. Для нахождения оптимального значения функции полезности вектор состояния по динамическим переменным (К, R°, RC) дискретизируется по определенной решетке и рассматриваются только переходы, обеспечивающие неотрицательность резервов и добычи. Для каждого перехода из состояния (К, R°, Rc) в состояние (К‘, R°,RC) значения для прочих статичных переменных выбираются таким образом, чтобы максимизировать полезность от текущего потребления при заданных ограничениях, для чего формулируются условия оптимальности для этой подзадачи и решается нелинейная система уравнений, состоящая из условий оптимальности Куна - Таккера, максимизирующих полезность индивида и условий равновесия, которые могут быть записаны в виде
К = Ку + К,
L = Ly + Ls, aAK“-1L^ E1-a-9 = (1 - a
P AK“LУ-1E^-“-9 = (1 - a
- p)АК"L9Е-"-9ӨВК Ө-1 Lp Н1-Ө-Р1 y y й й I
-
P)AK“L9 Е-^-РуВК® ЕР-1 Н 1 - Ө - р ,
(И)
E — S + о + с,
S = ВКӨ L^H 1-ө-^.
Система уравнений (11) решается по шести переменным: Ку,Кй,Ly,Ls,E,S. Общий труд L является экзогенно заданным в модели. Переменные о и с для данной задачи определяются вне системы в рамках переходов по сетке из R в R', а капитал К сам является узлом сетки. Далее система (11) может быть сведена к нелинейному уравнению относи-телыю Z := -^:
a(o + с) =
ВК ө L^
(Н (1 - Z) + Z)
Р ( — ^ ((1 -a - p)(1 - Z)Ө - a— ).
Рекуррентное уравнение (10) не имеет аналитических решений, поэтому мы будем использовать численные методы, дающие приближенные решения. Для нахождения приближенного решения нами будет использоваться простейший алгоритм поиска оптимальных последовательностей, основанный на теореме о сжимающих отображениях (Value Function Iteration Algorithm), поскольку оператор оптимальности Беллмана - это сжимающее отображение в бесконечной норме. Коротко основные шаги данного алгоритма могут быть описаны следующим образом.
Алгоритм 1. Поиск оптимальной последовательности детерминированной модели общего равновесия.
Шаг 1. Выбор решетки поиска объема п:
V = {Kx,K2,...,Kn}, Ki < Kj , i <3 = 1, 2, ...п, К° = R ,R<° ,..., R° }, R° > RO ,i <з = 1, 2, ...п,
R? = {R? ,R? ,...,Rn }, R? > R^ ,i < 3 = 1, 2, ...п.
Шаг 2. Инициализация значения функции r0ij ») V i,j,k = 1, 2,...п.
Шаг 3. Для поиска функции Д1, j») на следующем шаге и связанной с ней функции политики И 1 j k ) V i,j,k = 1,...п, необходимо найти индексы (г*, 3*,к*\ максимизирующие выражение (10). Установим И1 = (i*,j*,к*) и
4 j» K^R°X ) =
С fa , R°, Rf , Ki* , R°* ,Rf* )1 " - 1
1 — ст
+ Д0
1 + P
(Ki* ,R° R ) .
Шаг 4. Проверка сходимости: если
11Д0 — '" х <Е ^fa, Е> 0 (13)
(или если функция политики оставалась неизменной в течение ряда последовательных итераций), останавливаем алгоритм, иначе заменяем г0, И0 на д1 и И1 соответственно и, переходя к следующей итерации, возвращаемся к шагу 3.
2.2. Калибровка модели
Производство товаров и услуг конечного потребления Yst в текущий момент времени t возьмем равным сумме ВВП 18 укрупненных регионов в мире за 2017 год, что согласно данным The World Bank’s Development Indicators (WDI) [10] составляет 78.72 триллионов долларов США. Мировые потребности нефти и газа по данным WDI составляют 324.56 (in quad Btus), угля - 161.11 (in quad Btus), возобновляемые источники энергии - 84.64 (in quad Btus). Принимая цену нефти марки West Texas Intermediate в 50.8 долларов за баррель в 2017 году и предполагая, что один баррель нефти содержит 5.7 • 106 Btus, цена на нефть составит 8.91 • 10-6 долларов США за Btu. Аналогичные расчеты дают цену на газ в 2017 году 5.7• 10-6 за Btu, а цену на уголь 11.5 • 10-6 доллара США за Btu. Учитывая, что в рассматриваемой нами модели ресурсы нефти и газа трактуются как единый ресурс, а также их стоимости и мировые потребности в них, будем считать, что стоимость этого ресурса рассчитывается как средневзвешенная и равна 7.57 • 10-6 долларов США за Btu.
Далее нашей задачей является калибровка параметров а и 3. показывающих доли труда и капитала в общем объеме затрат для производственного сектора. Оценку для меры 1 — а — 3 рассчитаем, как отношение общего энергопотребления к мировому ВВП. Чтобы определить значения параметров а и 3, мы предполагаем, что одна треть этой оставшейся доли выпуска приходится на капитал, а остальная часть относится к труду. При такой конфигурации мы получим а = 0.287 и 3 = 0.575 соответственно.
В качестве общего значения использованного труда L и земельных ресурсов Н возмем нормированные значения, равные 1. Параметры эластичностей для альтернативной энергетики Ө и р, согласно уравнению (5) из [11], принимаем равными 0.13 и 0.27 соответственно. При калибровке уровней общей факторной производительности в секторах производства конечных товаров и экологически чистой энергии мы принимаем 10-процентную годовую норму амортизации капитала 8 в год. Ставка межвременного предпочтения р откалибрована на уровне 1.45 процента в год. В предложенной нами модели мы будем рассматривать 10-летние периоды. При пересчете нормы амортизации капитала 8 и ставки временного предпочтения р на 10-летний период получим 65.13 и 15.48 процентов за 10-летний период соответственно. Коэффициент относительного неприятия риска ст установлен равным 1.45, основываясь на [10].
Далее для калибровки параметра уровня совокупной факторной производительности для производственного сектора А может быть использовано уравнение (14), описывающее производство товаров и услуг конечного потребления Y по технологии Кобба - Дугласа, а именно:
Y = АК“t L^ tE1t' . (14)
УП yv-
С помощью уравнения Эйлера мы может рассчитать стационарное значение капитала, равное 207.65. Совокупная факторная производительность А в 2017 году, согласно уравнению (14), будет равна 9.69. Аналогичным образом может быть рассчитан уровень совокупной факторной производительности для энергетического сектора В. Согласно последнему уравнению системы (11) и отраслевым распределениям совокупного капитала и труда, для стационарного состояния В составляет 129.97.
Таблица, расположенная ниже, показывает необходимые параметры модели.
Таблица!
Параметры модели в детерминированном случае
|
Параметр |
Значение |
Параметр |
Значение |
Параметр |
Значение |
|
a |
0.287 |
ст |
1.45 |
Y |
78.72 |
|
3 |
0.575 |
Р |
0.1548 |
В |
129.98 |
|
Ө |
0.13 |
8 |
0.6513 |
А |
9.69 |
|
р |
0.27 |
Е |
0.001 |
Н |
1 |
Основываясь на [12], мы калибруем доступные в мире запасы нефти и газа до R q = 1000GtC и глобальные доступные запасы угля до R q = 2700 GtC. Издержки нефти и газа составляют 38,96 долларов за баррель нефти и 58 долларов за 1000 кубических метров газа, что эквивалентно 6.84 • 10-6 и 1.55 • 10-6 долларов США за Btu соответственно. Таким образом, стоимость издержек агрегата будет составлять 4.63 • 10-6 долларов США за Btu. Издержки угля возмем равными 9.26 • 10-6 долларов США за Btu.
2.3. Численные результаты для детерминированной модели реального делового цикла
Учитывая многомерность задачи оптимизации (8), прямое использование алгоритма итерации функции ценности приводит к экспоненциальному росту бюджета вычислений. Для сокращения количества вычислительных операций в программе реализации численного эксперимента будем использовать аппроксимацию функции полезности г полиномами третьей степени вида X • /3, где X = (1, Xi,..., Xg,..., XpXj,..., XiXjXk) и i,j,k = 1,.. .1, a вектор 3 имеет размерность, соответствующую X. Для этого случайным образом выбираем некоторую нерегулярную сетку {/*, R^, ^р} меньшего объема m из существующей сетки {С, В,0, Rc^ объема п и применим ранее упомянутый в разделе 2.1 алгоритм итерации функции полезности по выбранной случайным образом нерегулярной сетке. Все последующие шаги алгоритма работают с выбранной неравномерной сеткой. В качестве стартового решения будем использовать нулевое решение. В случае достижения желаемой точно- сти алгоритма далее производим аппроксимацию функции г с помощью метода наименьших квадратов полиномами третьей степени, который основан на минимизации функции (г — ж • 3)2. Для улучшения точности аппроксимации полиномами коэффициенты регрессии могут быть рассчитаны как средние значения коэффициентов, оцененных при повторных прогонах алгоритма с другим случайным выбором нерегулярной сетки {К*, 'RO, ^^} меньшего объема т. Далее, с помощью усредненных коэффициентов регрессии аппроксимируем функцию г на исходи ой сетке -[К, R°, Rc^ объема п
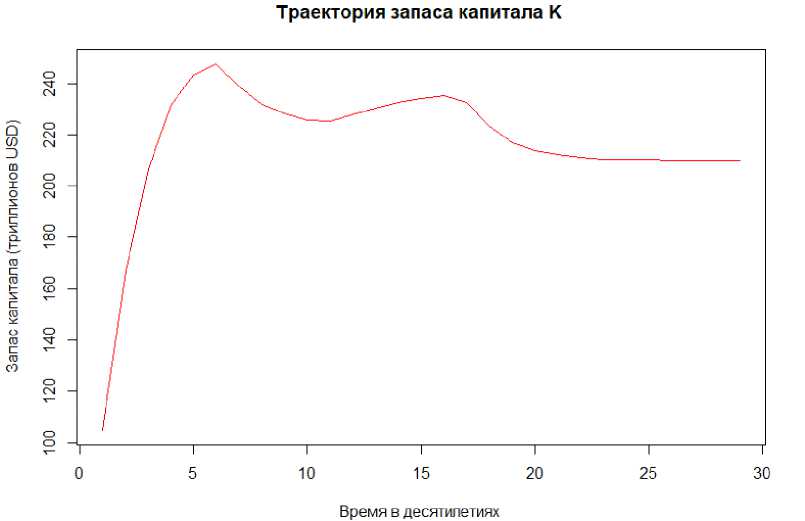
Рис. 1. Траектория запаса, капитала.
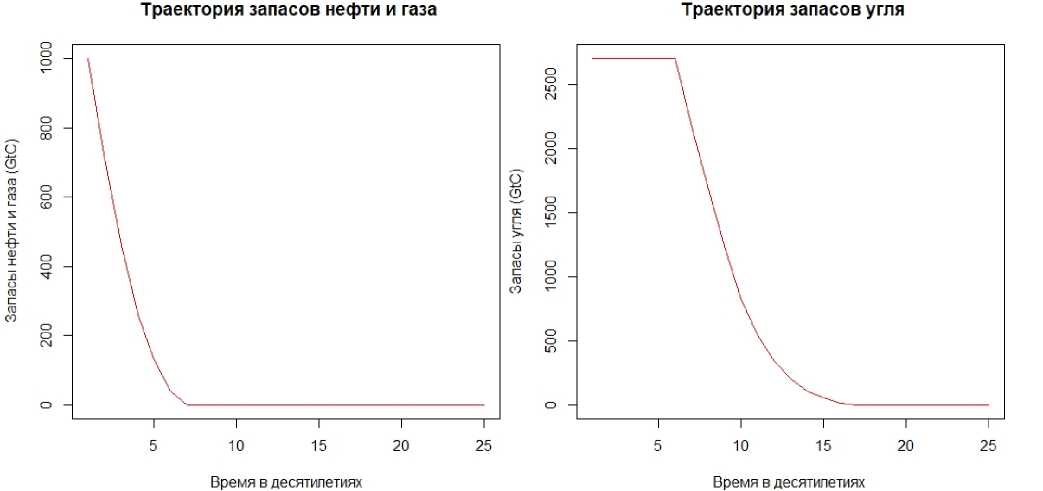
Рис. 2. Траектория запасов углеводородов
Зададим значения параметров модели, которые были описаны выше, и проанализируем работу описанного алгоритма. В качестве регулярной сетки для капитала К был выбран интервал [0.5К*, 1.5К*].
На рис. 1 и 2 показана оптимальная динамика переменных по времени. Здесь мы видим, что в первую очередь используется тот ресурс, затраты на добычу которого минимальны. В нашем случае это нефть. Далее важно отметить, что в моменты истощения запасов угля, нефти и газа наша экономика оказывается на верхнем участке седловой траектории.
3. Динамическая стохастическая модель центрального планирования3.1. Описание модели
Теперь рассмотрим случай для более широкого класса задач экономики, когда не все параметры детерминированы и могут принимать случайные значения, независящие от состояния экономики в прошлом. Рассмотрим постановку ранее описанной задачи при условии, что уровень производительности чистой энергии В является дискретной случайной величиной и принимает m значений. Каждому значению Вг случайной величины В соответствует вероятность г (для всех г = 1,..., s и ^D^i г = 1). Учитывая инвестиционное решение домохозяйства в текущем периоде Ki, его будущее потребление является случайной величиной с реализациями Ci (Вгу Следовательно, ожидаемая функция полезности домохозяйства на протяжении всей жизни равна.
с 1-^ 1 х 1 ГС1-сг - 1 "I
V(Kt,R?,Ry,Bt )= 1 — a + g (1 + p^ Et[ 1 - a ], (15)
где Et — условные математические ожидания в момент времени t. Таким образом, стохастическая задача Рамсея на бесконечном горизонте может быть представлена в следующем виде:
^ 1 г с1—ст 1 "I max Ut = V 7---—E —--- (16)
C t ,ct+1,... t (1 + p)3 Д 1 -a J '
при условиях (9). Используя подход динамического программирования к стохастической задаче, мы имеем следующее стохастическое функциональное уравнение:
v(K,Ro,RC, В) = max
' K‘,C,Ky,Ks,E,S ‘by ,Ls,o,c,Ro ,RC
C (K, Ro,RC ,K\R’0,R'C )1 " - 1
1 -a +
+-^E[r(K’,R’0,RC,В’) |B]) , 1 + P где условное математическое ожидание E [• | В] определяется как
E[r(K‘, R’0 ,RC,В') I В = г] = ^r(K‘,R‘0 ,RC,Д)р2: (18)
zeQ и p::’ ^ элементы матрицы переходных вероятностей Р. В наших дальнейших исследованиях мы будем использовать дискретную случайну величину В принимающую два значения: В = Втах с вероятностью г и В = В с вероятностью 1 - г, где Втах - значение параметра В, при значении которого используется только чистая энергия, а добыча угля отсутствует.
3.2. Калибровка модели
Значения параметров модели, расчитанные для случая детерминированной модели центрального планирования в разделе 2.2, являются актуальными для нашего последующего численного эксперимента. Далее нам необходимо откалибровать значение шокового уровня совокупной факторной производительности для энергетического сектора В max. Пусть затраты на добычу углеводородных энергоноситрелей удовлетворяют условию Хо < Хс тогда для экономической целесообразности использования чистой энергии цена энергии будет лежать в интервале (хо,Хс) а значение Bmax можно рассчитать из условия отсутствия добычи угля. И наконец, необходимо задать матрицу переходных состояний при условии того, что значение параметра B остается на этом же уровне на каждом последующем временном шаге, совершенном после достижения шокового уровня совокупной факторной производительности параметра Bmax. Учитывая вышеописанное условие, примем матрицу
переходных вероятностей вида P =
( 1 0.05
0 0.95
)
При такой конфигурации и затратах на
добычу агрегата хо = 4.63 • 10 6, угля хс = 9.26 • 10 6 долларов США за Btu значение для
шокового уровня совокупной факторной производительности для энергетического сектора будет составлять Bmax = 1801.95. Таблица 2 показывает необходимые параметры модели.
Т а б л и ц а 2
Параметры модели в стохастическом случае
|
Параметр |
Значение |
Параметр |
Значение |
Параметр |
Значение |
|
a |
0.287 |
a |
1.45 |
B |
129.98 |
|
3 |
0.575 |
Р |
0.1548 |
B max |
1801.95 |
|
ө |
0.13 |
6 |
0.6513 |
L |
1 |
|
V |
0.27 |
е |
0.001 |
Н |
1 |
3.3. Численный эксперимент стохастический модели общего равновесия
Аналогично описанному выше случаю детерминированнной модели и учитывая многомерность задачи оптимизации (16), будем использовать аппроксимацию функции г полиномами третьей степени вида ж • /3, где ж = (1,ж1,..., ж/,..., жг ж^ ,...,хгхj жк ) и i,j,k = 1,...l, а вектор 3 имеет размерность, соответствующую ж. Выбор нерегулярной решетки {/*, В®, Вр } меньшего объема m из существующей {/,В°,Вс} объема п и применение алгоритма итерации функции ценности будет производиться аналогично детерминированному примеру случайным образом. Для улучшения точности аппроксимации полиномами коэффициенты регрессии могут быть рассчитаны как средние значения коэффициентов, оцененых при повторных прогонах алгоритма с другим случайным выбором нерегулярной сетки {/*, В®, В*} меньшего объема m. Далее с помощью усредненных коэффициентов регрессии аппроксимируем функцию г на исходи ой сетке {/, В°, Вс} объема п. Основное существенное отличие в данном случае будет состоять в расчете функции условного математического ожидания E [г(Д | B], учитывая выражение (18). Для нахождения неизвестных коэффициентов 3г, i € No полинома будет также использован метод наименьших квадратов с помощью минимизации функции (E[г(Д | B] — ж • 3) ]• В контексте нашей постановки задачи в качестве произодственного шока нами будет использована дискретная случайная величина B, принимающая два значения. Важно также отметить, что при достижении максимального B max, модель сохраняет данное значение производственного параметра B и переходит в детерминированный случай. Таким образом, для реализации вычислительного эксперимента применительно к нашей модели используем следующий алгоритм.
Алгоритм 2. Поиск оптимальной последовательности стохастической модели общего равновесия.
Шаг 1. Выбор случайным образом неравномерной сетки {/*, В® , В*-' } меньшего объема m из существующей сетки /KL, В°, Вс^ объема п.
Шаг 2. В качестве стартового решения будем использовать векторное нулевое решение г 0 щШ Г = 1, . . . S.
Шаг 3. Пусть Р = pij - матрица переход пых состояний для i,j = 1,... ,s. Для поиска функции г1 на следующем шаге и связан ной с ней функции политики Һ1 V г = 1,...s необходимо найти индексы (г)Д*Д*), максимизирующие выражение (17). Установим ^ = (г*Дрк*) и
V1,(i,j,k) (Ki’ R , Rk, B) ) —
С ^Ki , RO , R^ , Ki* , RO ,R° )1 " - 1
1 — ст
+
+
1 s
—- VpTl^(Ki* , Rj* , Rk* , Bi)
1 + P =r J
Шаг 4. Проверка сходимости. Если для всех т — 1,..., s:
r01— г) L <е 1+p е>0 (20)
(или если функция политики оставаласв неизменной в течение ряда последовательных итераций) останавливаем алгоритм, иначе заменяем значение функции г° на следующем шаге на г1 и функции политики һ° на Һ1 и возвращаемся к шагу 3 алгоритма.
В случае достижения желаемой точности алгоритма аппроксимация функций г) и г0 на исходной сетке {/, КЯ, RC} может быть рассчитана аналогично детерминированному случаю методом наименьших квадратов.
Далее зададим значения параметров модели и проанализируем работу описанного выше алгоритма. В качестве регулярной сетки для капитала K был выбран интервал [0.5Kg, 1.5K*], где Kg и Kg - стационарные значения для капитала при значениях параметра B — B и B — Bmax На рис. 3 и 4 показана оптимальная динамика переменных по времени.
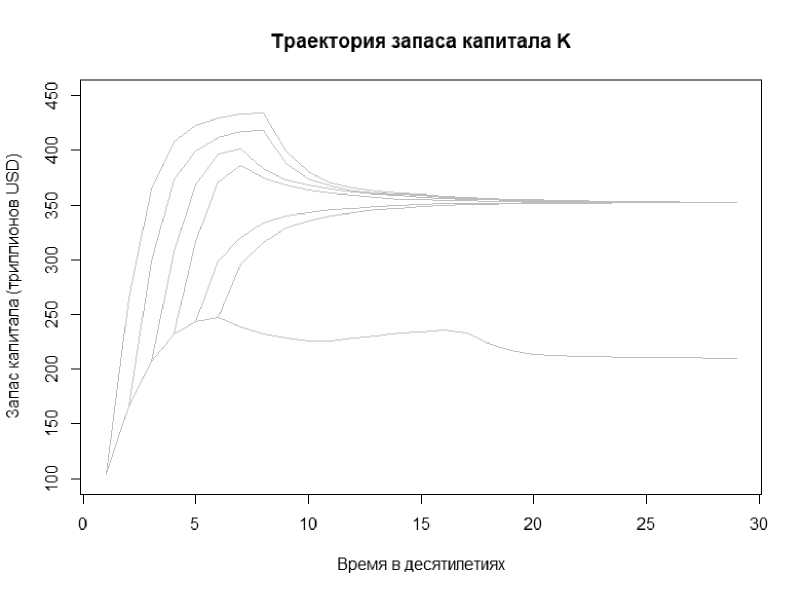
Рис. 3. Траектория запаса, капитала.
Здесь мы видим, что ресурс, затраты на. добычу которого минимальны, используется первым, как и в детерминированном случае. В нашей сегодняшней постановке задачи это нефть. Однако в отличие от детерминированного случая можно заметить, что в случае, когда B принимает критическое максимальное значение B — Bmax, уголь не используются, а используется только чистая энергия. Далее важно отметить, что в моменты истощения угля, газа или нефти наша экономика оказывается на верхнем участке седловой траектории, что полностью совпадает с детерминированным случаем. Асимптотическое поведение оптимального капитала, или, другими словами, стационарное значение капитала, равное К = 352.52, соответствует стационарному значению капитала при шоковом уровне совокупной факторной производительности для энергетического сектора Bmax. Данный факт можно обьяснить наличием поглощающего состояния в случае, если система принимает значение параметра В = Bmax.
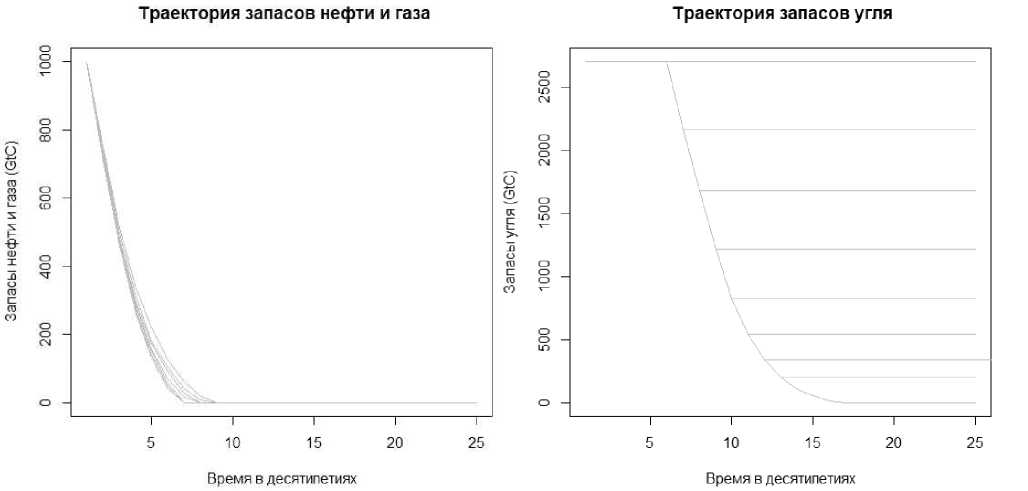
Рис. 4. Траектория запасов углеводородов
4. Международная стохастическая модель делового цикла4.1. Описание модели
Основной целью данной работы является переход к многомерной постановке задачи. Рассмотрим международную модель реального делового цикла (IRBC), в которой время t дискретно и бесконечно. В данной модели рассматривается экономика, где действуют домохозяйства и фирмы. Производство в секторе конечных товаров требует использования труда Ly,t, капитала Ky,t и энергии Et и описывается совокупной производственной функцией по технологии Кобба - Дугласа:
Y = AK“XtE^, (21)
, все параметры полностью соответствуют параметрам, использовавшимся в описании ранее построенных моделей. С другой стороны, конечный выпуск товара, цена которого Yt, может быть записан как уравнение бюджета потока:
-
Yt = Kt+1 + Ct - (1 - 5^Kt + XoOt + XcCt.(22)
Далее, общее использование энергии представимо в виде
Et = St + о, + Ct,(23)
а производство чистой энергии требует использования труда капитала земли и также осуществляется по технологии Кобба - Дугласа:
S = ВіК^ГЦН,1-9-9,(24)
где Bt — уровень производительности сектора чистой энергетики. Предполагается, что совокупное предложение земли фиксировано. Заметим также, что Bt — случайная дискретная величина, принимающая два значения (B, B) по аналогии с рассмотренней ранее постановкой задачи.
Фирмы в обоих секторах, действующие на рынке совершенной конкуренции, решают задачу по максимизации прибыли. Запишем условия максимизации прибыли для каждого из двух секторов. Для сектора товаров конечного потребления условия, максимизирующие прибыль, будут выглядеть следующим образом:
aAK“- 1 L^E1-0- = rt + 5,
PAK^L^ EE—-—-9 = wt, (25)
,
(1 _a -р) AK“tL^tE-“- = pt, , где rt - реальная процентная ставка, wt - реальная ставка заработной платы и pt - цена энергии. Для максимизации прибыли в секторе экологически чистой энергии требуется выполнение следующих условий:
PtGBt K^-Ч^Н 1—ө—^ = rt + 5, pt pBt K®,t L^ 1H1—ө—^ = wt, (26)
(1 - Ө -Д ptBtK^H—ө—^ = vt, где vt - рентная цена земли. В контексте данной модели нами будет рассмотрено три страны (агента), (г = 1, 2, 3), каждая из которых использует свой накопленный основной капитал at G R±, чтобы производить конечный товар, который можно использовать для инвестиций и для потребления Ct G R±. Первый агент располагает запасами нефти и газа, второй -угля, а третий агент имеет потребность в угле, нефти, газе и получает рентный доход на землю, обладая правами на ее использование. Далее, мы рассмотрим нашу модель с точки зрения домохозяйств.
Таким образом, репрезентативное домохозяйство каждой страны решает следующие проблемы оптимизации (с бесконечным горизонтом).
Имеется репрезентативное домохозяйство с функцией полезности
Ut = Et
∞
Е ө± j=0
1 1 — с
HL
1 -
a
где Өt±1 := Өt / (1 + p (Ct)) = Өtр (Ct) - эндогенный коэффициент дисконтирования, который зависит от среднего потребления товара в экономике (агента), Өо = 1 и a - коэффициент относительного неприятия риска, Et - условное математическое ожидание, зависящее от информации, доступной на момент времени t. Следуя [13], [14], [15], функция дисконтирования р (Ct) задается выражением
Р (Ct) = (1 + Ct)—, где ^ > 0. Тогда имеем (1 + p(Ct))—1 = (1 + Ct)—^. Как и в [15], [16] и [17], введение эндогенного фактора дисконтирования обеспечивает достижение стационарного процесса благосостояния. Таким образом, каждое домохозяйство максимизирует свою функцию полезности u1 (Ct) при существующих условиях. Соответственно, задача оптимизации первого агента будет представлена следующим образом:
max
Г(1) (1)
^ t ^t+v"
ut1) = Et
∞
^2 ө (1) (C±221
-
СТ
-
5=0
-
a
при условиях
°t+1 + Ct + XoOt — ^tL^ ) + (1 + Tt)a^ + pt0t, В°+1 — В? — ot ,
— В°ц < 0,
- ot < 0, где У^ — 0(1)^(Ct‘1)) и 3(Ct(1)) — (1 + С^) §1. Чтобы найти решение данной оптимизационной задачи (27) максимизации функции полезности, мы используем теорему Куна -Таккера. Применение данной теоремы к задаче (27) дает следующие условия Куна -Таккера первого порядка:
(С( )) (pt — Xo) — 1° + Р° — 0,
CV — wtLt^ + (1 + Tt)^t^ + Pt ot — °t+1 — Xo0t,
(Ct(1))
—er
E
(1 + ^
1 + т , +1
. (Oe. ’
1 ° lt
, ' 1V. E [+11 - — 0’
(1+C,(1))
Bt+1 — B° — ot ’ otP° — 0’
В°+1^° — 0, где Z°, p° и p° — неотрицательные множители Лагранжа для ограничений в задаче (27), а условия otр*° — 0, В°1^° — 0 являются условиями дополняющей нежесткости.
Учитывая, что второй агент располагает ресурсами угля, но не обладает запасами нефти и газа, задача оптимизации второго агента примет вид
°t+1 + Ct + XcCt — ш , Lt + (1 + Tt ^t + pt Ct’
В^ 1 — В? — Ct,
— ВЯ1 < 0,
— с , < 0.
Условия оптимальности Куна - Таккера для этой задачи таковы:
(Ct )) (pt — Xc) — 1? + Pt — 0’
щ(2) (2) (2) (2)
Ct — utLt + (1 + Tt)at + ptCt — й , + 1 — XcCt’
( c , (2) )
e
(1 + Ct(2))
§2
Et
1 + т , +1
. (cS)e. ’
1c lt
—
(1 + Ct(2f
Et [Z?+1] — ^? — 0,
В?+1 — В? — Ct, ct Pt — 0,
В?+1 ^? — 0, где Iх, рр и рХ — неотрицательные множители Лагранжа для ограничений в задаче (30), а условия ctр^ = 0, К^^рС = 0 являются условиями дополняющей нежесткости. Наконец, задача оптимизации третьего агента может быть записана следующим образом:
max n = Et
,(3) r(3) t
' t ^t+V"
^ (3) 1 — ст
^ ^(3) (C t + j )
У 61 —Г—7
1 =0
-
Г
при условии
°t +i + Ct^ = ^t L () + (Г + r't)at^ + vtH. (34)
Условия оптимальности Куна - Таккера для задачи оптимизации функции полезности для третьего агента примут вид
C
-----Г---ж Et
( г + 48, ) < 3
Г + Tt +1
. c
c3 = ШД? + (Г + rt)at3) + vtH - at +)i .
Также необходимо учесть условия равновесия на рынках. Суммарные значения капитала и труда равны сумме их отраслевых показателей по аналогии с ранее описанной постановкой задачи в разделе 2.1, а именно:
Kt = Ky,t + Ks,t, Lt = L y,t + Ls,t.
В то же время с учетом капитала, труда и потребления каждого агента имеем
Kt = at1 ) + a 1 2 + °t3), Lt = -« +-t2) +-t3), Ct = ct(1) + ct(2) + ct(3),
где a^, L^, C^ соответствуют активам, труду и потреблению агента, г = Г, 2, 3, на данный момент времени t. С учетом всего вышеизложенного, получаем стохастическую систему нелинейных функциональных уравнений, а именно:
Kt = Ky,t + Ks,t, Lt = Ly,t + LS,t ’ aAK^ TL^t E^a- = rt + 5, ^AK^y- 1 Et-- = wt, (1 -a -p)AK“XtЕГ- = Pt, Et = St + ot + ct’
St = BtK^,tHт-ө-^
Pt 6BtK8- TL^tH т-ө-^ = rt + 5, pt pBtK8^- TH т-ө-^ = wt,
-
8 ф = vt ,
(1 - Ө -p) ptBtK^H Kt = а(т + a(2) + at3), Lt = LtT) +Lt2) +Lt3), а,
а,
a
' t+т
' t+т
' t+т
P° +T
+ c( т)
+ c( 2)
+ Ct(3)
= P°
+ XoOt = Wt L(1) + (1 + rt )atT) + Pt ot , + XcCt = Wt L(2) + (1 + rt )at2) + pt ct,
= Wt L^
+ (1 + rt^a^ + vtH,
p C pC ^t +T = P^t
(Ct(T))-"
(Ct(2))-"
(Ct(3))-"
-
-
ot,
ct ’
( 1 + C^1
Et
. ( С '+т ) ". ’
E
(1 + C^52
------1----Et (1 + Ct(3) ) 5 3
. (CS)". ’
.(О". ’
(C t ) ) (pt - Xo) - Z° + p° = 0’
(
C(
)
)
(pt —
Xc)
—
Z
1 ° Zt
-
1с Zt
-
ot Pt ct Pt
( 1 + C,(Tf
( 1 + C<2) ) i2
= 0 ,
= 0 ,
Et [ Z°+1 ] - Ф° = 0,
Et [ ZC +1 ] - ^с = 0,
R° +i v° = о, Кн т Р = о.
4.2. Расчетный эксперимент для международной стохастический модели делового цикла
Нашей основной задачей является решение системы нелинейных уравнений (38). Два важных момента при решении этой системы состоят в следующем: во-первых, нужно записать выражения для условных математических ожиданий Et ''Д'! , Et [lt+i] и Et [l^], Учитывая описанный выше подход и применяя пакет Rnlsr, использующий вариант алгоритма Нэша - Марквардта (Алгоритм Левенберга - Марквардта) для нелинейного метода наименьших квадратов, могут быть найдены коэффициенты аппроксимации /3- Далее, используя упрощения, сделанные для системы (11), мы можем аналогичным образом представить функциональную зависимость от базисных переменных всех остальных неизвестных переменных в момент времени t. Используя блок уравнений с 21-го по 24-е системы (38), могут быть вычислены необходимые множители Лагранжа для данной оптимизационнной задачи. Наконец, рекуррентные уравнения с 1-го по 17-е системы (38) позволят рассчитать значения базисных переменных на следующем шаге в момент времени t + 1. Говоря о калибровке данного расчетного эксперимента, необходимо рассчитать парамет функций (1 + С(і^ ры ^і для г = 1, 2, 3, что может быть сделано, учитывая сходимость и 1 + rt при достижении области стационарного состояния системы. Также следует от метить, что калибровку, сделанную в разделах 2 и 3, мы будем полностью использовать далее. Распределение трудовых ресурсов между агентами примем равными 0.3, 0.4 и 0.3 соответственно. На рис. 5 представлены полученные результаты расчетного эксперимента. На основании графиков мы можем заметить, что при данной постановке задачи углево- дородные ресурсы используются одновременно, что подтверждает желание каждого агента максимизировать значение функции полезности. Асимптотическое поведение функции суммарного международного оптимального капитала полностью соответвует ранее описанному нами в разделе 3 случаю, благодаря наличию поглощающего состояния в случае, когда система принимает значение параметра В = В max. Полученные нами графики также подтверждают распределение оптимального капитала каждого агента в стационарном состоянии в соответствии с распределением трудовых ресурсов между агентами. Рис. 5. Траектории переменных модели
5. Заключение В работе на базе динамической стохастической модели общего равновесия с наличием неопределенности в будущем спросе показано, что в экономике с несколькими исчерпаемыми ресурсами с различными издержками добычи, когда у каждого ресурса есть свой собственник и разделения риска между агентами не происходит, на рынке одновременно торгуются ресурсы с высокими и низкими издержками добычи. В рассматриваемой постановке задачи предполагается, что с некоторой вероятностью в будущем спрос на ресурс с высокими издержками добычи может резко сократиться (что в модели реализуется за счет стохастического улучшения в технологии производства альтернативных источников энергии). Это побуждает собственника ресурса с высокими издержками добычи извлекать природный ресурс в текущие периоды времени одновременно с ненулевой добычей более дешевого ресурса. Полученный результат можно косвенно применить к обсуждению текущей экономической ситуации для РФ. Так, существует высокая вероятность снижения доходов от экспорта энергоносителей в будущем из-за намерений недружественных стран постепенно отказываться от покупки российских энергоносителей, вводить ограничения на цены покупки российской нефти и т.д., что, в свою очередь, формирует условия для наличия дисконта по продаже российских энергоносителей в дружественные страны. В условиях наличия ожиданий резкого сокращения спроса на российские энергоносители в будущем у собственников угольных компаний возникают стимулы интенсифицировать добычу угля в текущие периоды времени, что может привести к снижению цен на энергоресурсы и совокупных дисконтированных доходов от продажи российских углеводородов. В описанных условиях собственники угольных компаний могут расширять производство и лоббировать государственную поддержку угольной отрасли, например, за счет субсидий на транспортировку угля, что уже наблюдается в текущих реалиях, когда как в эффективном равновесии может потребоваться обратное - снижение добычи угля. Поскольку все имеющиеся энергоресурсы с высокой долей вероятности продать на внешние рынки не удастся, то оптимальной стратегией может являться продажа наиболее дорогих и рентабельных энергоресурсов. Сокращение экспорта угля РФ позволило бы создать в некоторой степени дефицит на мировом рынке энергетики и повысить цены на российские нефть и газ, снизить дисконт. Также снижение экспорта угля позволило бы высвободить логистические ресурсы для транспортировки нефти. А. В. Полбин выполнил исследование для данной статьи при финансовой поддержке Российского научного фонда (грант № 21-18-00126). Вклад автора в статью: систематизация литературы, постановка задачи, спецификация модели, интерпретация результатов.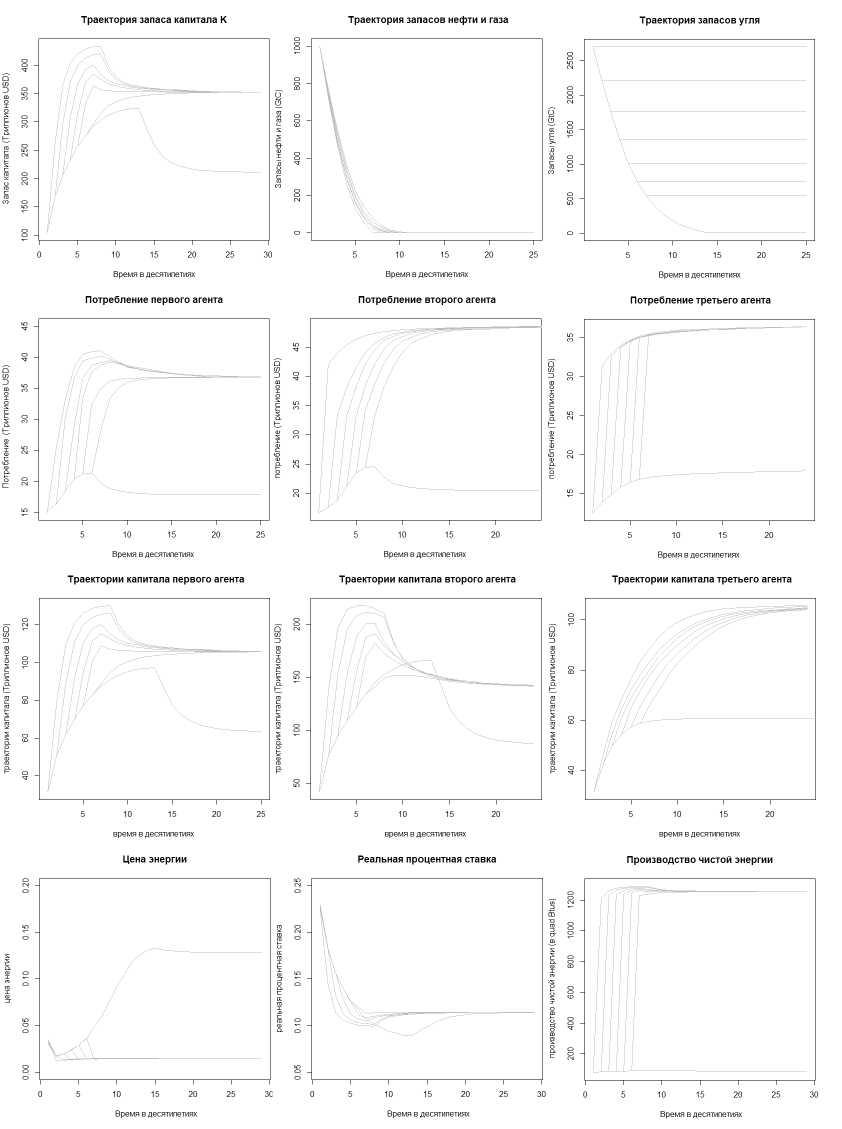
Список литературы Порядок извлечения ресурсов с различными издержками добычи в условиях наличия неопределенности в будущем спросе
- Hotelling H. The economics of exhaustible resources // Journal of Political Economy. 1931. V. 39, N 2. P. 137–175.
- Herfindahl, O.C. Depletion and economic theory. In: Gaffney, M. (Ed.), Extractive Resources and Taxation // Madison University of Wisconsin Press. 1967. P. 63–90.
- Solow R.M., Wan F.Y. Extraction costs in the theory of exhaustible resources // The Bell Journal of Economics. 1976. V. 7, N 2. P. 359–370.
- Holland S.P. Set-up costs and the existence of competitive equilibrium when extraction capacity is limited // Journal of Environmental Economics and Managementn. 2003. V.46, N 2. P.539–556.
- Amigues J.P., Favard P., Gaudet G., Moreaux M. On the optimal order of natural resource use when the capacity of the inexhaustible substitute is limited // Journal of Economic Theory. 1998. V. 80, N 1. P. 153–170.
- Chakravorty U., Krulce D. L. Heterogeneous demand and order of resource extraction // Econometrica: Journal of the Econometric Society. 1994. P. 1445–1452.
- Benchekroun H., van der Meijden G., Withagen C. OPEC, unconventional oil and climate change – on the importance of the order of extraction // Journal of Environmental Economics and Management. 2020. V. 104, P. 102384.
- Gaudet G., Lasserre P. The efficient use of multiple sources of a nonrenewable resource under supply cost uncertainty // International Economic Review. 2011. V. 52, N 1. P. 245–3258.
- Golosov M., Hassler J., Krusell P., Tsyvinski A. Optimal taxes on fossil fuel in general equilibrium // Econometrica. 2014. V. 82, N 1. P. 41–88.
- Kotlikoff L.J., Kubler F., Polbin A., Scheidegger S. Can today’s and tomorrow’s world uniformly gain from carbon taxation? // National Bureau of Economic Research. 2021. N w29224.
- Kotlikoff L., Kubler F., Polbin A., Sachs J., Scheidegger, S. Making carbon taxation a generational win win // International Economic Review. 2021. N 62(1). P. 3–46.
- McGlade C., Ekins P. The geographical distribution of fossil fuels unused when limiting global warming to 2 C // Nature. 2015. V. 517, N 7533. P. 187–190.
- Kollmann R. Incomplete asset markets and the cross-country consumption correlation puzzle // Journal of Economic Dynamics and Control. 1996. V. 20, N 5. P. 945–961.
- Corsetti G., Dedola L., Leduc S. International risk sharing and the transmission of productivity shocks // The Review of Economic Studies. 2008. V. 75, N 2. P. 443–473.
- Boileau M., Normandin M. Closing international real business cycle models with restricted financial markets // Journal of International Money and Finance. 2008. V. 27, N 5. P. 733–756.
- Schmitt-Grohe S., Uribe M. Closing small open economy models // Journal of international Economics. 2003. V. 61, N 1. P. 163–185.
- Devereux M. B., Sutherland A. Country portfolios in open economy macro-models // Journal of the european economic Association. 2011. V. 9, N 2. P. 337–369.


