Поршневая тепловая машина для преобразования энергии и производства работы на транспорте

По состоянию на сегодня одной из важных составляющих энергетических ресурсов на транспорте являются жидкие углеводородные топлива, производимые из нефти, природные запасы которой ограничены. В балансе потребления топливно-энергетических ресурсов (ТЭР) на долю транспорта и транспортных систем приходится 25–30 %. В этой связи важной проблемой современной энергетики, наряду с решением задач по альтернативным источникам энергии, является проблема режима расходования ТЭР, относящихся к числу исчерпаемых. Сегодня основным средством преобразования заключенной в топливе энергии и производства механической работы, в том числе и на транспорте, является поршневая тепловая машина с кривошипно-шатунным механизмом (КШМ). Однако двигатели с КШМ наряду с достоинствами обладают и рядом недостатков. К одним из них относятся сложность и высокая стоимость этих механизмов (20–30 % от стоимости двигателя в целом).

Названные обстоятельства побуждают исследователей к отысканию новых схем и типов машин-двигателей, свободных от указанных недостатков. Примером таких решений может служить ряд конструктивных схем машин, предложенных различными авторами [1–4]. Важной особенностью таких машин-двигателей является непосредственное преобразование возвратно-поступательного движения поршня во вращательное грузового вала. Использование механизма преобразования движения позволяет исключить из конструктивной схемы двигателя шатун и кривошип. Благодаря этому в схеме сил, действующих на поршень, удаётся исключить так называемую нормальную силу, действующую перпендикулярно поверхности зеркала цилиндра и обуславливающую рост затрат на преодоление трения в сопряжении «поршень-цилиндр». Это обстоятельство (снижение трения) обуславливает повышение механического и эффективного КПД бескри-вошипной машины (БКМ).

Поскольку закон движения поршня в таких двигателях отличен от закона, обеспечиваемого КШМ, при их создании необходимо использование иного расчётного инструментария.

Конструктивные особенности и рабочий цикл БКМ

Особенности расчета БКМ вытекают из анализа конструктивной схемы двигателя, в котором механизм преобразования движения вынесен за пределы поршня (рис. 1). В нём возвратнопоступательное движение поршня 1 посредством штока 2 передаётся каретке 3. В каретке установлена ось 4, цапфы которой перемещаются по криволинейному замкнутому (например синусоидальному) пазу (беговой дорожке), образованному криволинейными торцевыми поверхностями втулок 5 и 6. Движение цапф по беговой дорожке обуславливает вращательное (вокруг оси двигателя) движение оси 4 и каретки 3. Каретка в плоскости, перпендикулярной оси 4, охвачена

Расчет и конструирование

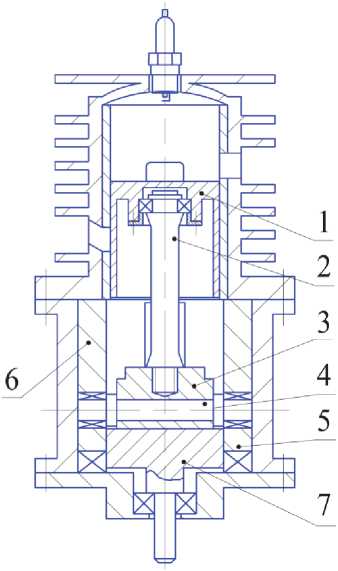
стержнями двухрожкового грузового вала 7. Вращательное движение каретки, благодаря такой кинематической связи, передается грузовому валу 7.

Беговая дорожка, образованная криволинейными профилями торцевых поверхностей втулок 5 и 6, в общем случае может быть многопериодной. Например, может иметь профиль двухпериодной синусоиды. В этом случае одному полному обороту грузового вала соответствует четыре хода поршня (два возвратно-поступательных). Таким образом, если иметь ввиду схему реализации 2-тактного цикла, то за один оборот грузового вала таких циклов реализуется два. Следовательно, применительно к прочим равным условиям, работа, производимая тепловой машиной (например, транспортным двигателем) выполненной по приводимой схеме, в два раза может превысить работу, производимую за такой же отрезок времени, традиционной машиной с КШМ.

Рис. 1. Конструктивная схема бескривошипной тепловой машины-двигателя (применительно к случаю реализации 2-тактного рабочего цикла)

Рабочий цикл бескривошипной тепловой машины-двигателя

Характер изменения параметров состояния рабочего тела (РТ) в цилиндре двигателя в течение цикла определяется многими факторами. В частности: особенностями подвода (или отвода) теплоты к РТ, динамикой выгорания топлива, кинематикой движения поршня, режимом нагрузки.

Кинематика движения поршня массово распространённых машин с КШМ описывается ши- роко известными соотношениями (по этой причине здесь эти соотношения не приводятся).

Применительно к условиям реализации рабочего цикла (РЦ) в бескривошипной машине рас- сматриваемой схемы с двухпериодной беговой дорожкой кинематические особенности движения поршня могут быть отображены уравнениями:

)

s = ^ • (1 — cos2a) v = ы • 5п • sin2a у = 2 • ы2 • 5п • cos2a

где s, v, j – текущие значения перемещения, скорости и ускорения поршня соответственно; α – текущий угол поворота грузового вала; Sп – полное перемещение (ход) поршня; ω – угловая час- тота вращения.

Приведённые кинематические соотношения (1) для БКМ и соответствующие широко известные соотношения для машин с КШМ позволяют сделать (применительно к числено равным значениям полных перемещений S п поршня) сопоставление текущих параметров, характеризующих кинематику этих машин (рис. 2).

Ещё раз отметим то обстоятельство, что в БКМ с двухпериодной беговой дорожкой за один оборот грузового вала совершается четыре хода поршня, а в двигателе с КШМ – два. Поэтому сопоставление кинематических параметров машин целесообразно выполнить, учитывая период изменения этих параметров. Для двигателя с КШМ он составляет 360 град., для БКМ – 180. Иными словами s, v, j для названной цели удобно представить функциями относительного времени t = — = —, где tц, ац - соответственно временная и фазовая (по углу поворота вала) продол-^ц йц жительность цикла. Графики, приведённые на рис. 2, выполнены с учётом названных обстоятельств. Анализ кинематических параметров машин (см. рис. 2), позволяет отметить, что характер их протекания подобен. Экстремальные значения s, v, j приведены в табл. 1.

Численные значения параметров кинематики в экстремальных точках

Таблица 1

	s , м		v , м/с			j , м/с2
^^^^а t	0	0,5	0,25	0,208	0,5	0	0,5
КШМ	0,034	0	–16,91	–17,43 – макс.	0	–21199	12450
БКМ	0,034	0	–16,91 – макс.	–	0	–16824,93	16824

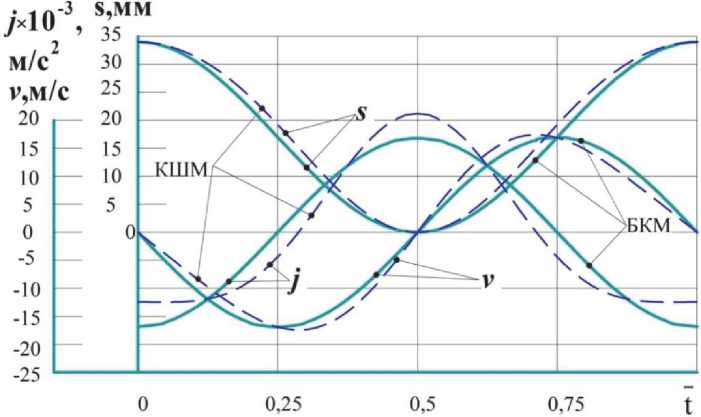
Рис. 2. Характер протекания кинематических параметров двигателей в функции относительного времени при 1_ц = 6,3 • 10^-3 , с

Моделирование параметров состояния РТ в процессе сжатия

Функцию для текущего перемещения поршня s в (1) перепишем в виде:

|-(1-cos2a) =|-о(а),                                                      (2)

здесь о(а) - кинематическая функция хода поршня (численное значение её определяется, в нашем случае, только текущим α).

По аналогии с Wiebe [5] используя (2), запишем функцию, характеризующую изменение объёма РТ в цилиндре:

ф(а) = 1 + ^ • о(а),                                                             (3)

в которой ε – степень сжатия.

Тогда система уравнений для определения параметров состояния рабочего тела (давления p и температуры T ) в процессе сжатия запишется в виде:

• - ^Г;П ]

^м^Г, ф(а) = 1 + ^ • а(а), о(а) = 1 — cos2a.

где n 1 – показатель политропического процесса.

Исходными условиями для решения системы являются численные значения параметров в начальной точке (точка « а » индикаторной диаграммы – положение в НМТ): p = p a ; T = T a ; ψ(α) = ψ(α a ); σ(α) = σ(α a ). Параметры состояния РТ в процессе сжатия применительно к двигателю с КШМ отображаются системой, аналогичной (4) [6]. Но в ней для определения значений σ(α) используется уравнение

о(а) = 1 + ^ — (cosa + ^ • V1 — Л2 • sin2 а).

где Л = г/£_ш (г - радиус кривошипа, £_ш - длина шатуна).

Расчет и конструирование

Моделирование параметров состояния РТ в процессе сгорания

Параметры состояния РТ в процессе сгорания (прежде всего p и T) являются функцией многих факторов. В этой связи определение их текущих значений в этот период РЦ выполняется пошагово на базе методов численного интегрирования. Нами использован метод расчёта, предложенный И.И. Вибе [5], достаточно подробно изложенный в [6].

Важной составляющей метода является расчёт количеств теплоты, сообщаемых РТ вследствие горения топлива на каждом достаточно малом шаге расчёта. При этом для описания характера выделения теплоты используется уравнение выгорания Вибе:

x = 1 — exp

/•t\ m+1l

-6.908 •(;;)   |

в котором t , t z – текущее время и продолжительность сгорания соответственно; m – показатель характера сгорания.

Для целей сопоставительных исследований (оценки качеств РЦ двигателя с КШМ и БКМ) необходимы численные значения параметров m и φ z , а также θ (угол опережения воспламенения). Это делалось на основании следующего. Полагалось, что характер горения углеводородных смесей определенного качества (например, характеризуемых одинаковыми значениями коэффициента избытка воздуха α) при близких численных значениях ε в 2- и 4-тактных двигателях во времени одинаков. Тогда значения m и t z , определённые для 4-тактных двигателей, можно распространить и на 2-тактные. Так, по результатам обобщения экспериментального материала по бензиновым 4-тактным двигателям, работающим на частотах вращения 3500…5600 мин^–1 с α = 0,85…0,95, установлено, что φ z находится в пределах 35…50 град. ПКВ, m = 3…3,5. Учитывая связь временного интервала и соответствующей ему фазы поворота вала (ф = 6 • п • t), определили, что продолжительность горения смеси названного качества находится в пределах 1,5 ■ 10^-3 ... 1,6 ■ 10^-3 с. Соответствующие значения θ отвечают временным интервалам горения, находящихся в диапазоне 0,7 ■ 10^-3 .„0,35 ■ 10^-3 с. Сказанное даёт основания для оценки численных значений 6 и ф z применительно к двигателям, работающим по 2-тактному циклу. Это, в свою очередь, позволяет расчётным путём выявить численные значения параметров, характеризующих состояние рабочего тела в процессе горения.

Отметим, что начальными условиями для расчёта горения являются параметры РТ, соответствующие завершению сжатия (момент, определяемый значением θ: точка y с соответствующими p_y , T_y , ν_y ).

Процесс расширения

Моделирование параметров в процессе расширения базируется на условии, что этот процесс является политропическим. Начальными условиями для расчёта являются численные значения параметров РТ в момент окончания сгорания (точка z на индикаторной диаграмме): p = p_z ; T = T_z ; ψ(α) = ψ(α z ); σ(α) = σ(α z ). Таким образом, система уравнений для расчёта текущих параметров имеет вид (применительно к БКМ):

• *)=^г )

  ^г(а)=< • t¹^] "²

  
  

  -1

  ^,

  
  
  
  

ф(а) = 1+^а(а),

о(а) = 1 — cos2a.

Для моделирования процесса в двигателе с КШМ используется система уравнений аналогичная (6). Но в ней σ(α) рассчитывается с учётом замечания, сделанного по поводу этой функции в тексте, касающегося моделирования параметров при сжатии.

Изменение параметров состояния РТ в течение РЦ для БКМ и для двигателя с КШМ иллюстрируется « p-ν » – диаграммой, рис. 3. На рис. 4 приведены графики изменения давлений и температур РТ в функции относительного времени. Сопоставительная оценка параметров по некоторым показателям цикла приводится в табл. 2.

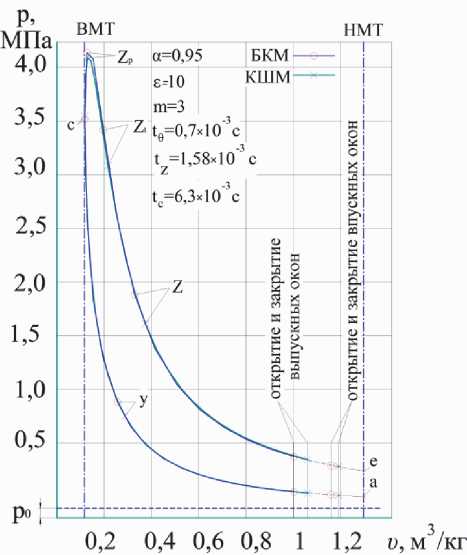
Рис. 3. Индикаторные « p-ν » диаграммы двигателей с КШМ и БКМ

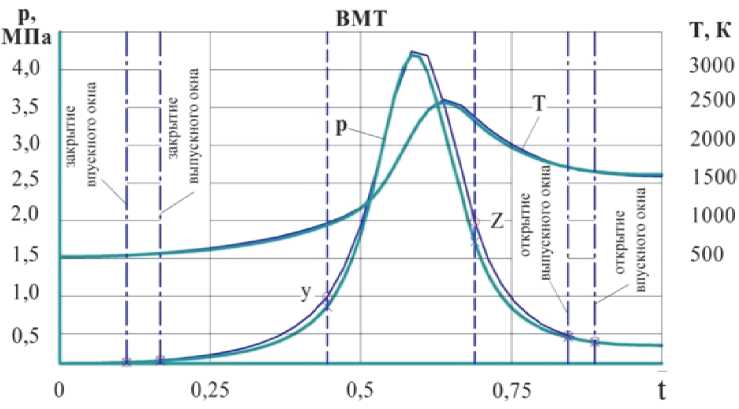
Рис. 4. Характер протекания давлений и температур РТ в функции относительного времени

Таблица 2

Сравнение основных термодинамических параметров двигателей

	P макс , МПа	α p макс, град. ПКВ	т „ . макс	α T макс, град. ПКВ	p i , МПа	η i	g i , г / (кВт·ч)
КШМ	4,19	10	2565	30	0,686	0,37	220
БКМ	4,24	5	2604	15	0,67	0,36	225

Расчётная оценка показателей РЦ бескривошипной поршневой тепловой машины и машины-двигателя с КШМ применительно к одинаковым условиям реализации РЦ (по величине ε, α, m , t z , t θ , S п ) даёт основания утверждать, что бескривошипн ы й двигатель по таким параметрам цикла как p макс , T макс , p i , η i не уступает поршневому двигателю с КШМ. При этом производимая им работа, приходящаяся на один оборот грузового вала, превышает (почти в два раза) работу, производимую соответствующим двигателем с КШМ.

Расчет и конструирование