Position Regulation and Anti-Swing Control of Overhead Gantry Inverted Pendulum (GIP) using Different Soft-computing Techniques

Published Online February 2016 in MECS

• I.    Introduction to GIP System

The basic configuration of GIP system comprises of a movable cart on which is mounted a rigid and massless pendulum. The pendulum is free to rotate without friction [1]. The dynamics of GIP resembles a Gantry crane, which is widely used in industries for transportation of suspended load [2]. These are highly non-linear systems and exhibits uncontrolled oscillations which causes both stability and safety hazards [3]. The objective is to quickly transfer the load to desired destination with minimum swing [4]. Recently various soft-computing techniques have been used for control and stabilization of GIP systems. Wahyudi and Jalani [5] designed an intelligent gantry crane system using fuzzy logic controllers which was further compared with classical PID controller. The results showed that fuzzy controllers were more robust to parameter variation as compared to

PID controllers. Al-Mousa [6] studied controllers based on two different techniques i.e. fuzzy and time delayed position feedback controller. The two controllers were further combined into a hybrid controller which showed good performance.

Mahfouf et al. [7] proposed a fuzzy logic based antisway control of overhead cranes. They designed a nonlinear model of overhead crane using two rule bases which takes into account a combination of both trolley and pendulum. The results indicate the feasibility of two rule base control strategy. Chang et al. [8] presented a twin fuzzy controller which deals with feedback information from position and swing angle of load. The proposed approach not only simplifies the designing procedure of crane but also reduces the number of fuzzy rules. Lee and Cho [9] proposed a fuzzy anti-swing control of a three-dimensional overhead crane. The control scheme consisted of position servo control and fuzzy logic control. The proposed controllers accurately controlled the crane position, rope length and suppresses load swing during hoisting and traverse motions of crane.

Choi et al. [10] proposed a neural network based two degree of freedom PID controller for controlling swing motion and position of gantry crane. Simulation results shows excellent performance of proposed controller. Bruins [11] presented a comparison between four control algorithm for gantry crane system. The different controllers were P-controller, cascade P-controller, fuzzy controller and an internal modal controller. Results showed that fuzzy controller gives best performance. Shojaei et al. [12] proposed a novel controller based on recurrent neural network and PID controller for Rotational inverted pendulum (RIP). They also presented an investigation study for stabilizing RIP using Genetic algorithm (GA). Solihin et al. [13] presented a fuzzy PID controller design for control of gantry crane. The proposed system utilizes fuzzy system as PID gain tuners for achieving desired performance. Arpaci and Ozguven [14] a non-linear model for an overhead crane system has been derived. An ANFIS controller has been developed and simulated in Matlab using training data from PID controller.

This paper elaborates a new methodological approach for comparative analysis of three different soft-computing techniques in Matlab. The comparison study is based on following control techniques i.e. fuzzy logic reasoning, ANFIS and Neural networks for position regulation and anti-swing control of GIP systems. The mathematical model of GIP was built in Matlab-Simulink and simulation results are shown with the help of graphs and tables which proved the validity of proposed study.

• II. Mathematical Model of GIP System

A two-dimensional view of GIP on cart is shown in figure 1.0 as considered from Pal and Mudi [15]. It comprises of a load of mass (m), attached to a cart of mass (M) with a rigid pendulum of length (L). The mass of the pendulum is considered to be negligible. A force (u) is applied to the cart in horizontal direction (x) while maintaining an angle (Ө) between pendulum and vertical axis (y).

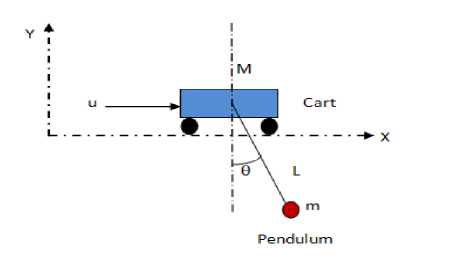
Fig.1.0. Gantry Inverted Pendulum

Mathematical modeling of GIP was done using Newton's second law "Ref. 16". The complete system was further divided into two subsystems i.e. cart and pendulum. The free body diagrams (FBD) of both the systems are shown in figure 1.1 and figure 1.2 respectively. Where, F is the longitudnal force exerted by the pendulum.

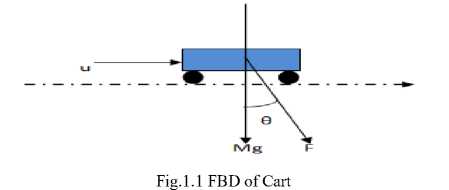
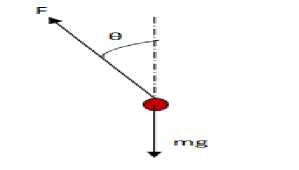
Fig.1.2. FBD of Pendulum

The governing mathematical equations for GIP system were derived using FBD of above sub-systems. The equations of motions for cart and pendulum systems are given below

• (a)    Equations for Cart

• i.    Along X-axis

Mx = u + F sin 0(1)

• ii.    Along Y-axis

F cos0 + Mg = 0

• (b)    Equation for Pendulum

• i.    Along X-axis

d2            .             „  .„ m. —((x + Lsin 0) = — Fsin0(3)

at2               '

• ii.    Along Y-axis

m.^(L cos 0) = -F cos 0 + mg(4)

The above equations were used for determining angular acceleration of pendulum (Ӫ) and acceleration of cart (ẍ).

0 = - [ u cos 0 + m sin 0 ( L 0 ²cos 0 + g ) + Mg sin 0 ] (5) ( M + m sin² 0 ) L

X = u + m sin 0 ( L0² + g cos 0 ) ( M + m sin² 0 )

Using eq. (5) and eq. (6) the Matlab Simulink model of GIP was build.

• III.    Building Simulink Of Gip System

Initially a Matlab Simulink of GIP was built which was further integrated into a sub-system. A view of GIP Simulink and its complete sub-system are shown in figure 1.3 and figure 1.4 respectively.

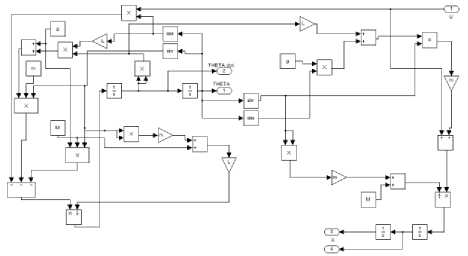
Fig.1.3. Simulink of GIP system

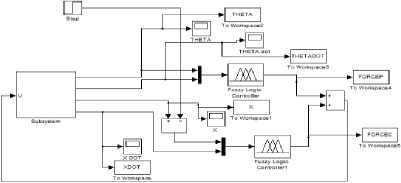
Fig.1.4. Simulink of GIP sub-system

• IV.    Fuzzy Control Of GIP System

The study considers Mamdani based fuzzy inference system (M-FIS) "Ref. 17" with gbell membership functions (MF's) "Ref. 18" for designing of Fuzzy logic controller (FLC's) "Ref. 19". The study considers seven linguistic variables (namely NL-negative large, NM-negative medium, NS-negative small, ZE-zero, PSpositive small, PM-positive medium and PL-positive large) for defining a set of 49 if-then fuzzy rules "Ref. 20". A view of gbell MF's and surface viewers for both cart and pendulum controllers are shown from figure 1.5 to figure 1.8.

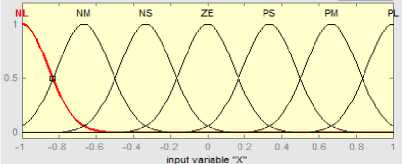
Fig.1.5. MF's for Cart position

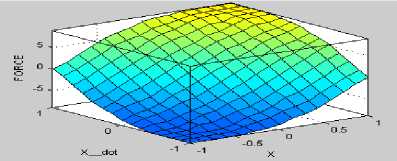
Fig.1.6 Surface viewer for Cart controller

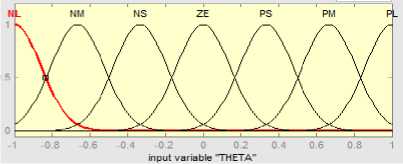
Fig.1.7 MF's for Pendulum angle

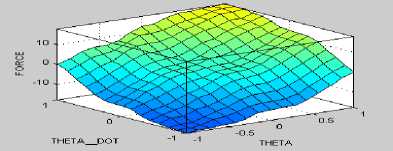
Fig.1.8 Surface viewer for Pendulum controller

• V. Anfis Control Of GIP System

ANFIS "Ref. 21" belongs to a class of artificial neural network "Ref. 22" which is based on Takagi-Sugeno fuzzy inference system "Ref. 23". The training in ANFIS was done using Hybrid learning algorithm "Ref. 24" which is a combination of Back-propagation "Ref. 25" and least square method "Ref. 26". The Grid partition method was further used for building an initial FIS structure.

A total of 65 data sets were collected from simulation results of fuzzy controller. These data sets were further used for training of ANFIS controller. The loading of data sets for cart and pendulum controller in ANFIS are shown in figure 1.9 and figure 2.0 respectively.

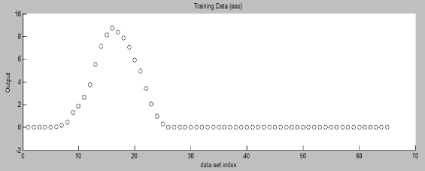
Fig.1.9 Loading of data sets for Cart controller

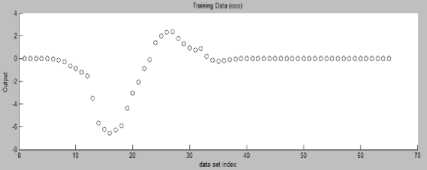
Fig.2.0 Loading of data sets for Pendulum controller

The training error tolerance for both cart and pendulum controllers were set to zero. The training of cart and pendulum controllers in ANFIS are shown in figure 2.1 and figure 2.2 respectively.

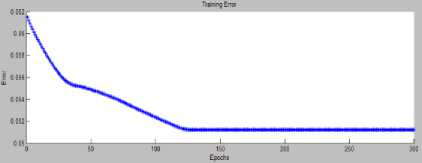
Fig.2.1 Training for Cart controller

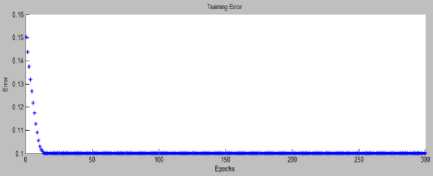
Fig.2.2 Training for Pendulum controller

This study considers gaussian MF's (3 Nos.) for building FIS structure in ANFIS. During training the MF's and fuzzy rules were modified according to training data sets. A view of MF's and surface viewer obtained after training of cart controller are shown in figure 2.3 and figure 2.4 respectively.

A view of output responses and comparison of performance parameters using fuzzy and ANFIS controllers are shown with the help of graphs and tables below.

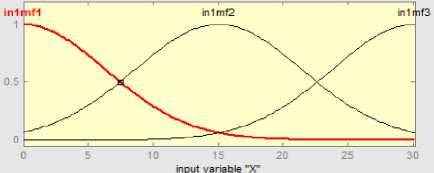
Fig.2.3 MF's for Cart position after training

a. Cart Velocity Response

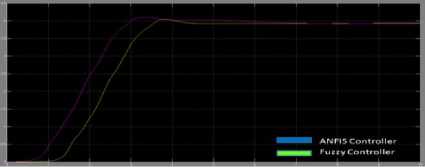
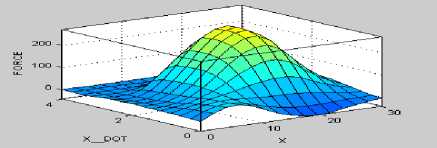
Fig.2.4 Surface viewer for Cart controller after training

Table 1.2 Comparison of Cart velocity response

Performance parameter	Fuzzy controller	ANFIS controller
Settling time (sec)	4.5 sec	4.0 sec
Maximum Overshoot (degree)	4.0º	4.1º
Steady state error	0	0

In this study the relationship between number of MF's and training error has also been illustrated. A view of training error obtained for different number of MF's are shown in table 1.0.

Table 1.0 Error for cart and pendulum controllers

Nos. of MF's	Training Error (Cart controller)	Training Error (Pendulum controller)
3	0.052373	0.012194
4	0.039958	0.001448
5	0.020751	0.0017271
6	0.0041908	0.0012238
7	0.0043663	0.0010999
8	0.0034438	0.0011094
9	0.0034577	0.0010848
10	0.0030623	0.0011328
11	0.002998	0.0010151
12	0.0029749	0.0010933
13	0.0029482	0.00085599
14	0.00067823	0.00096947

It is clearly observed from the table 1.0 that with increase in number of MF's the training error for the controllers decreases. Therefore an adequate number of MF's can considered for obtaining optimal training error.

• VI.    Output Responses of Fuzzy and Anfis Controller

The simulation time considered for the study was 10 sec. The values of different parameters considered for simulation are given in table 1.1

• b.    Pendulum angle response

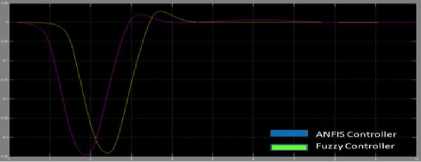
Table 1.3 Comparison of Pendulum angle response

Performance parameter	Fuzzy controller	ANFIS controller
Settling time (sec)	4.6 sec	4.0 sec
Maximum Overshoot (degree)	-0.33 º to 0.03 º	-0.33 º to 0.02 º
Steady state error	0	0

• c.    Pendulum angular velocity response

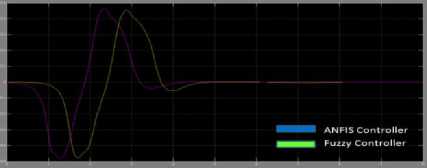
Table 1.1 Values of different parameters

Parameter	Value
mass of cart (M)	1Kg
mass of Pendulum (m)	0.1 Kg
acceleration due to gravity (g)	9.81m/s2
length of the pendulum (L)	1metre

Table 1.4 Comparison of Pendulum angular velocity response

Performance parameter	Fuzzy controller	ANFIS controller
Settling time (sec)	4.6 sec	4.2 sec
Maximum Overshoot (degree)	-0.48 º to 0.44 º	-0.49 º to 0.45 º
Steady state error	0	0

• VII.    Nn's Control of GIP System

In this study we have used Neural network fitting tool (nftool) "Ref. 27" for designing of NN's controllers. Training of controllers was done using Levenberg-Marquardt "Ref. 28" back-propagation algorithm. Training automatically stops when generalization stops improving, as indicated by increase in the Mean square error (MSE) of the validation samples. The MSE was used for measuring performance of the controllers. It is basically the average squared difference between outputs and targets. Lower values of MSE are considered better, zero means no error. Regression (R) values measure the correlation between outputs and targets. An R value of 1 indicates a close relationship whereas R value of 0 indicates a random relationship.

A total of 65 data sets or samples were collected from simulation results of fuzzy controllers. The data sets were further divided randomly into training, validation and testing samples. A view of randomly divided data is shown in table 1.5

neurons (N) can considered for obtaining optimal values of MSE and R. The training of samples multiple times will generate different results due to different initial conditions and sampling. Neural network architecture was build using 20 neurons in the hidden layer and 1 neuron in the output layer. A view of neural network architecture is shown in figure 2.8

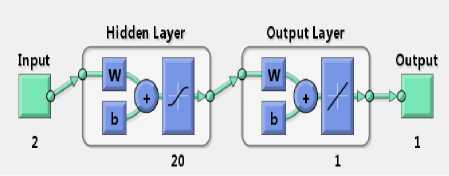
Fig.2.8 Neural network architecture

The Regression (R) plots for training, validation, testing sample and overall regression response after training of 20 neurons in the hidden layer are shown from figure 2.9 to figure 3.2.

Table 1.5 Randomly divided samples

Samples	Percentage	Nos. of samples
Training	70%	45
Validation	15%	10
Testing	15%	10

The study also illustrates the effect of variation in number of hidden neurons (N) on the MSE and R. During training, the network adapts to decrease the error on the training patterns. A view of values of MSE and R for different values of N are given in table 1.6.

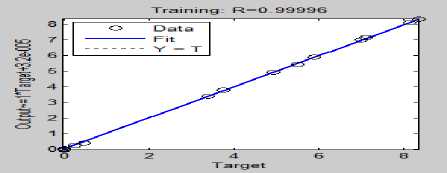
Fig.2.9 Regression response for training sample

N=20
	Training sample	Validation sample	Testing sample
MSE	4.7236e-4	2.2388e-2	1.3334e-2
R	9.9996e-1	9.9835e-1	9.9959e-1
N=21
MSE	2.7297e-3	2.1750e-3	3.3970e-2
R	9.9977e-1	9.9968e-1	9.9953e-1
N=22
MSE	1.3986e-2	3.3647e-2	1.8557e-2
R	9.9939e-1	9.9795e-1	9.9911e-1
N=23
MSE	1.5480e-2	8.6439e-3	1.6635e-2
R	9.9837e-1	9.9942e-1	9.9961e-1
N=24
MSE	5.7634e-3	1.7234e-3	2.0782e-2
R	9.9992e-1	9.9989e-1	9.9621e-1
N=25
MSE	6.4066e-3	1.4475e-3	8.1264e-3
R	9.9941e-1	9.9986e-1	9.9983e-1

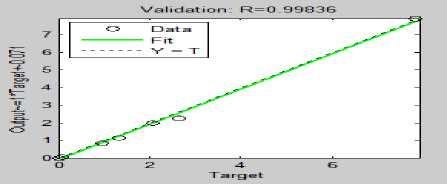
Fig.3.0 Regression response for validation sample

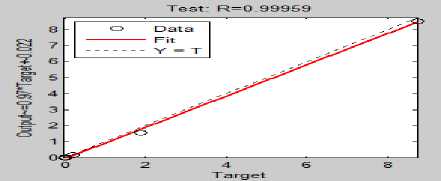
Fig.3.1 Regression response for testing sample

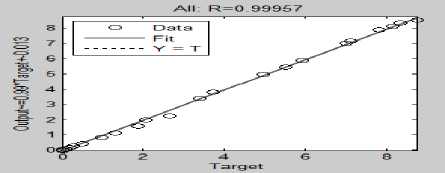
Fig.3.2 Overall Regression response

As can been seen from table 1.6 the values of MSE and R changes with N. Therefore an adequate number of

• VIII.    Output Responses of Neural Network Controllers

The output responses for cart and pendulum using NN's controller are shown from figure 3.3 to figure 3.6. The results shows that NN's controller was not able to control the GIP system. Hence further refinement in values of MSE and R is needed for improvement.

• a.    Cart response

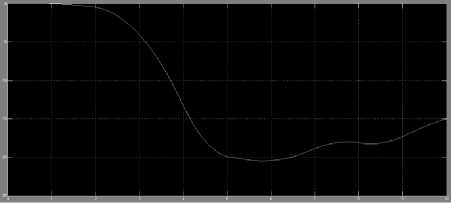
Fig.3.3 Cart position response

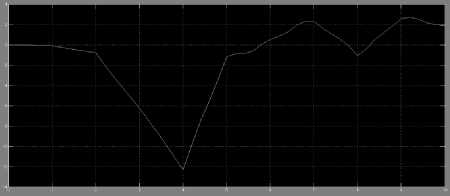
Fig.3.4 Cart velocity response

• b.    Pendulum response

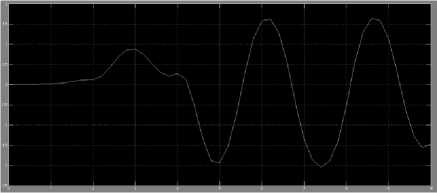
Fig.3.5 Pendulum angle response

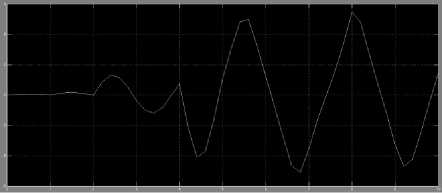
Fig.3.6 Pendulum angular velocity response

• IX.    Conclusion

The control objective of this study to apply different soft computing techniques for stabilization of GIP system has been achieved. It is observed from the simulation results that both fuzzy and ANFIS controllers were able to stabilize the non-linear GIP system. The ANFIS controller shows better results in terms of settling time. The ANFIS controller stabilizes the system within 4.2 sec whereas fuzzy controller takes 4.6 sec to control the complete GIP system. Both of these controllers shows excellent response in terms of maximum overshoot and steady state error. It is observed that ANFIS technique shows an excellent learning ability with negligible training error. The training error obtained using 3 MF's for cart and pendulum controller were 0.052373 and 0.012194 respectively. It is also concluded that with increase in number of MF's the training error tolerance for ANFIS controllers decreases.

The NN's controller shows a good learning ability with overall Regression value of 0.99957 using 20 neurons in the hidden layer. The NN's controller was unable to stabilize the GIP system (refer figure 3.3 to figure 3.6). It was also observed that R and MSE values changes with variation in the number of hidden neurons (N). Therefore an optimal number of hidden neurons can be selected for proper designing of NN's controllers. It is also recommended to apply other optimization techniques like Genetic algorithm (GA) "Ref. 29", Particle swarm optimization (PSO) "Ref. 30", Sliding mode control "Ref. 31" for control and stabilization of non-linear and complex GIP systems.