Positive solutions to Sobolev type equations with relatively p-sectorial operators

Let U, F be real Banach spaces, the operators L E L (U; F) (i.e. L is linear and continuous operator) and M E C l( U ; F) (i.e. M is linear, closed, and densely defined operator). Let us consider the nonhomogeneous linear Sobolev type equation

Li = Mu + f.                            (1)

For the first time in history, the term “Sobolev type equations” appeared in the paper [1]. Currently, these equations occupy a very vast area among non-classical equations of mathematical physics, and are studied in very different aspects (see, for example, [2, 3]). Besides that, there are many treatises in which Sobolev type equations have other names, for instance, “degenerate equations” [4] or “partial differential equations and systems not solvable with respect to the highest-order derivative” [5]. In this paper, the terms [4] and [5] are considered to be synonyms for the term [1–3]. We are interested in the conditions under which equation (1) (ker L = { 0 } is allowed) has a unique positive solution.

The main tool to find such conditions is the theory of positive degenerative holomorphic semigroups of operators. (Recall that the semigroup of operators V • = { V ^t : t E R } is called degenerate if s-lim V ^t = I [2, Ch. 2]). Therefore, in Section 1 of this paper, we t —>0

present the basic facts of the theory of positive holomorphic semigroups of operators given in [6, Ch. 1] and [7, Ch. 2 and Ch. 3]. Then, in Section 2, we extend the results of Section 1 to positive degenerate holomorphic semigroups of operators. The main result of Section 2 is the sufficient and necessary condition of the positivity of degenerate holomorphic semigroups of operators. Note that this result is published for the first time. Section 3 contains the main results of this paper. First, we consider the linear homogeneous Sobolev type equation

Lui = Mu.                                  (2)

It turns out that if the operator M is strongly (L,p)-sectorial on the right for some p E {0} U N [2, Ch. 2], then the resolving semigroup of equation (2) is a degenerate holomorphic semigroup of operators U• = {Ut : t E R}. If, in addition, the operator M is strongly (L,p)-sectorial for some p E {0} U N [2, Ch. 2] and the semigroup U• is positive, then, for all u0 E U1 ПU+, there exists the unique positive solution u = u(t) to the Cauchy problem tlim Mt) - uo) = 0 (3)

of equation (2) such that u(t) = Utu0. Here U1 is the phase space of equation (2), U+ is the proper generative cone, and U = (U, || • ||u, U+) is the Banach lattice. Then we state sufficient conditions for the existence of the unique positive solution to the Showalter– Sidorov problem t—0+ P(u(t) — uo)=0 (4)

for equation (1). Here the operator P = s-lim U t is the unit of the semigroup U • , which is t —0

a projector by construction [2]. Note that, in this case, the positivity of the semigroup U ^• is not enough, and the Banach lattices U = ( U , || • ||u , U ₊ ) and F = (F, || • |f , F ₊ ) should be matched.

Further, we use the abstract results in order to construct a positive solution to Showalter–Sidorov problem (4) for an interpretation of abstract equation (1), where the operators L = diag{Lk(A)}, M = diag{Mk(A)}, while Lk(A) and Mk (A) are polynomials with real coefficients such that deg Lk(A) < deg Mk (A) Vk E N.

In this case, it is necessary to switch classical Sobolev spaces to Sobolev spaces of sequences [8,9]

m l _q

∞ mq u = {uk} :          |uk1

k=1

< ^ J* ,

m E R , q E [1, + ro ),

which are analogues of Sobolev spaces Wm. Here {Ak} C R+ is a monotonically increasing sequence such that lim Ak = +^. The paper [10] was the first to find conditions for the k→∞ existence of a degenerate positive resolving group of operators of equation (2) in the case of the strongly positive relatively bounded operator M , as well as conditions for the existence of a positive solution to problems (2), (3) and (1), (4), where the operators L = L(Л), M = M(Л) are polynomials with real coefficients such that deg L > deg M.

The methods and approaches developed in the paper can be widely used to solve economic and technical problems in which the positivity of a solution is of practical importance (for example, studying the process of pressure of a filtered fluid). The proposed spaces of sequences allow to study problems in quasi-Sobolev spaces of sequences that are quasi-Banach spaces [8,9] in the case of q E (0,1). The need to consider such non-classical spaces takes place in a number of technical problems [11]. Also, diagonal operators that can be investigated by the proposed methods arise in closed economic systems (that is, when the rate of production depends only on the output of the product itself) described by balance models (Leontief type models) [12].

1.    Positive Holomorphic Semigroups of Operators

Consider the real Banach space V, the operator A : dom A С V ^ V such that A G C l(V) (i.e., A is linear, closed, and densely defined). Denote by p(A) = { m 6 C : (Д ! — A) ^-1 G L (V) } the resolvent set of the operator A, where L (B) is the space of linear continuous operators defined on B, a(A) = C \ p( A) is the spectrum of the operator A. Slightly departing from standard [6, Ch. 1], we define the sectorial operator.

Definition 1. The operator A G C l( V ) is called sectorial, if

• (i)    there exist the constants a G R and 0 G ( П ,n) such that

S a,e = { m G C : | arg(^ — a) | < 0, m = a } С p(A);

• (ii)    there exists the constant K >  1 such that

K

■I — A)       • for any m G Sa,e.

Definition 2. The mapping V • G C “ ( R ₊ ; L (V)) is called a semigroup of operators, if

V ^s V t v = V ^s+t v V s, t G R ₊ V v G V.                       (5)

A semigroup is called holomorphic , if the semigroup can be continued in some sector containing the ray R ₊ with preservation of property (5).

Definition 3. The operator A G C l(B) is called the infinitesimal generator of the semigroup V • = { V t : t G R ₊ } , if Av = lim (V t v — v)t ^-1 for all v G dom A. If A is the infinitesimal generator of the semigroup V • , then we write V t = e ^At .

Theorem 1. [6, Ch. 1] The following statements are equivalent.

• (i)    The operator A G C l(B) is sectorial.

• (ii)    The operator A G C l(B) is the infinitesimal generator of the holomorphic semigroup { e ^A : t G R ₊ } having the form

  _e tA

  
  

= 9™ A^I - a) 1 e^dM 2ni J t G R+,

г where the contour Г С Sa,e is such that | argm| ^ 0 for |m| ^ w, m G Г.

Remark 1. If the operator A is sectorial, then there exists a unit of the semigroup { e ^tA : t G R ₊ } given by the formula I = s- lim e ^tA , where “s-lim” denotes strong (i.e. pointwise) limit.

Corollary 1. [6, Ch. 1] Let A G Cl(B) be a sectorial operator. Then eAt

= s- lim f l — yA^ k→∞     k

t G R + .

Note that Corollary 1 is true under more weak condition on the operator A.

Definition 4. The real Banach space B = (B, || • ||b ) is called the ordered Banach space B = ( b, I • I b , > b ) if there exists the order relation > b , which satisfies the axioms of reflexivity, transitivity, antisymmetry, and is consistent with the vector structure of the space B , i.e.

• (i)    (x > _B У ) ^ (ax > _b ay ) for any x, y G B and for all a G R ₊ ,

• (ii)    (x > _B y) ^ (x + z > _B У + z) for any x, y G B and for all z G B.

If, in addition, the order relation > b is consistent with the metric structure of the space B, i.e. for all x G B there exist x ₊ , x - G B such that

• (iii)    (x ₊ > _b 0) Л (x - > _b 0) Л (x = x ₊ — x - ),

• ^(iv)    (| x | > b | y I ) ^ ^{( | x |} B >  ||y ||b) ^for any y ^{G B} , then the ordered Banach space B = (B, || • \ b , > b ) is called the Banach lattice. (Here | x | = x ₊ + x - ).

As an example, we note the following Banach lattices:

• (i)    the space of continuous functions C (Q; R ) for any domain Q C R n , if the order >

is defined by the formula (f > g) О (f (x) > g(x) for all x G Q) with f+(x) = max{f (x), 0}, f-(x) = max{-f (x), 0}, xGU                      xGU

• (ii)    the Lebesgue space L q (Q; R ),q G [1, to) , Q C R n , if the order >  is defined by the formula (f >  g) О (f (x) >  g (x) for a.e (almost everywhere) x G Q) with f ₊ (x) = vraimax { f (x), 0 } , f - (x) = vraimax {— f (x), 0 } , xeQ                          xeQ

• (iii)    the sequence space l q , q G [1, to) , if the order >  is defined by the formula (x >  y) о (x k >  y k for all k G N ) with | x | = ( | x k | ),

• (iv)    the space R n endowed with any norm, if the order >  is defined by the formula (a >  b) О (a _k >  b k for all k = 1, n) with | a | = col( | a i | , | a ₂ | ,..., | a _n | ).

Note that not every ordered Banach space is a Banach lattice. Indeed, let C ¹ ([0,1]; R ) be a space of functions that are continuously differentiable on the interval [0,1] endowed with the norm

I x l = max | x(t) | + max | x ‘ (t) | . te[G,i] te[G,i]

Suppose that the order >  is given by the formula (x >  y) О (x(t) >  y(t) for all t G [0,1]). The order >  satisfies the axioms of reflexivity, transitivity and antisymmetry. In addition, the order >  is consistent with the vector structure of the space C ¹ ([0,1]; R ). However, the order >  is not consistent with the metric structure of the space C ¹ ([0,1]; R ). This fact is easy to establish by considering the functions x(t) = e and y(t) = e t for all t G [0,1].

Definition 5. Let B be a Banach space. A convex set C C B such that aC + в C C C for all a, в G R ₊ is called a cone. A cone C is called proper, if C П ( — C) = { 0 } , and generative, if B = C — C.

Let B be a Banach lattice, then (it is easy to see) B+ = {x G B : x > 0} is a proper generative cone. On the other hand, let B be a Banach space, and C C B be a proper generative cone. Let us introduce the order relation >b by the formula (x >b y) О (x — y G C). Then (B, || • ||b, >b) is an ordered Banach space but, taking into account the example of the functional space C1 ([0,1]; R), we see that B may not be a Banach lattice. Further, we well distinguish the ordered Banach space (B, || • ||b, >b) and the Banach lattice (B, || • ||b,B+).

Definition 6. (i) Let (B = (B, || • | B , B ₊ ) be a Banach lattice. The operator A E L (B) is called positive, if AB ₊ C B ₊ .

• (ii)    A semigroup of operators V • = { V t : t E R ₊ } is called positive, if V t V ₊ C V + for all t E R + .

• Theorem 2. Let B = (B, || • | B , B ₊ ) be a Banach lattice, and A E C l(B) be a sectorial operator. Then the following statements are equivalent.

• (i)    The resolvent R^(A) = (pI — A)^-1is a positive operator for sufficiently large p E R+.

• (ii)    The holomorphic semigroup {e^tA : t E R₊} is positive.

2.    Positive Degenerate Holomorphic Semigroups of Operators

Proof. (i)^(ii) is true by virtue of Corollary 1. (ii)^(i) is true by virtue of the ∞ representation [6, Ch. 1] R^(A) = J etAe-^tdt for all p > Re ^(A).

Let us construct degenerate positive holomorphic semigroups of operators. Suppose that U, F are Banach spaces, the operators L E L(U; F) (i.e. L is linear and continuous), M E Cl(U; F) (i.e. M is linear, closed, and densely defined). The foundation of our research is the theory of degenerate semigroups of operators and the phase space method described in [2, Ch. 3]. Let us give the necessary information on the theory of degenerate semigroups of operators in Banach spaces. Consider the L-resolvent set pL (M) = {p E C : (pL — M)-1 E L(F; U)} and the L-spectrum aL(M) = C \ pL(M) of the operator M, as well as the operator functions R"(M) = (pL — M)-1L and L"(M) = L(pL — M)-1, which are called the right and left L-resolvents of the operator M, respectively (see [2, Ch. 1]). Let pq E pL(M), q = 0,1,... ,p. The operator functions pp

RU (M) = IK(M)• L(M) = IP (M) k=0                         k=0

are called the right and left (L,p)-resolvents of the operator M, respectively.

Definition 7. [2, Ch. 3] The operator M is called p-sectorial with respect to the operator L with the number p E { 0 } U N (in short, (L,p)-sectorial ), if

• (i)    there exist the constants a E R and 0 E ( ⁿ , n) such that

S Le (M) = { p E C : | arg(p — a) | < 0,p = a } C p ^L (M );

• (ii)    there exists the constant K E R ₊ such that

K max {|R(^,p)(M)|l(u) , ||L(^,p)(M) Hl(F) } < ”

П |pq — a| q=0

for any p q E S L_e (M ), q = 0,1,...,p.

Lemma 1. [2, Ch. 3] Let the operator M be (L,p)-sectorial for some p E { 0 } U N . Then there exist the degenerate holomorphic semigroups of operators

U t = — [ RL (MVtdp and F t = — [ L L (M)e ^t dp. 2ni J    ^     '     '                    2ni J >^:     '

г

г

Recall [2, Ch. 3] that the semigroup V • is called degenerate, if s- lim V t = I . Here t E R ₊ , and the contour Г C S L _e (M ) is such that | arg^ | ^ 0 for ^ ^ to , ^ E Г. If V • E C ^ ( R . ; L (V)) is a degenerate holomorphic semigroup of operators, then we can define ker V • = { v E V : V t v = 0 3 1 E R ₊ } . Since the semigroups U • and F • are holomorphic, we set U ⁰ = ker U • , F ⁰ = ker F • . Let L ₀ be the restriction of the operator L to U ⁰ , and M ₀ be the restriction of the operator M to U ⁰ П dom M .

Theorem 3. [2, Ch. 3] Let the operator M be (L,p)-sectorial for some p E { 0 }U N . Then

• (i)    L 0 E L (U ⁰ ; F ⁰ ) and M o : U ⁰ П dom M ^ F ⁰ ;

• (ii)    there exists the inverse operator M ^—1 E L (F ⁰ ; U ⁰ );

• (iii)    the operator H = M ^—1 L ₀ E L (U ⁰ ) (G = L ₀ M ^-1 E L (F ° )) is nilpotent of degree less than or equal to p.

If V • E C ^ ( R . ; L (V)) is a degenerate holomorphic semigroup of operators, then we can define im V • = { v E V : lim V t v = v } . Since the semigroups U • and F • are holomorphic, we set U ¹ = im U • , F ¹ = im F • . Let L ₁ be the restriction of the operator L to U ¹ , and M ₁ be the restriction of the operator M to U ¹ П dom M . Then U ⁰ ф U ¹ C U and F ⁰ Ф F ¹ c F.

Definition 8. [2, Ch. 3] The operator M is called strongly (L,p)- sectorial on the right (on the left) for some p E { 0 } U N , if M is (L,p)-sectorial for some p E { 0 } U N and

A R L p) (M)(AL - M ^Muh <   co ' 's'     v u E dom M,

I A| П К I q=0

О where const = const(u) (there exists the lineal F, which is dense in F and such that

A M ( al - m ) -¹ LL„, ) (M )f B f <  ^co p ^nst    v f s F,

|λ|        |µq| q=0

where const = const(f)); A,^ _q E S L (M ), q = 0,1,...,p.

Remark 2. Without loss of generality, we can take a = 0 in Definition 7. Indeed, if we find the resolving semigroup of equation (2) { U t : t E R ₊ } for a = 0, then the semigroup { e^atU t : t E R ₊ } is resolving when a = 0.

Theorem 4. [2, Ch. 3] Let the operator M be (L,p)-sectorial on the right (on the left) for some p E { 0 } U N . Then there exists the projector P = s- lim U t (the projector Q = s- lim F t ). t^0+

Remark 3. It is easy to see that, under the conditions of Theorem 4, there exists the splitting of the space U and F, i.e.

U ⁰ Ф U ¹ = U and F ⁰ Ф F ¹ = F.

(A1)

Definition 9. [2, Ch. 3] The operator M is called strongly (L,p)-sectorial for some p E { 0 } U N , if M is strongly (L,p)-sectorial on the left for some p E { 0 } U N and

IK^L ^{- M} ) ^{1 L} L_u,p) ( ^M ) ^ L( F ; U ) <

const

p

I A| П К I q=0

for every A,p _q E S L (M ), q = 0,1,...,p.

Theorem 5. [2, Ch. 3] Let the operator M be strongly (L,p)-sectorial for some p E {0}UN. Then there exists the inverse operator L E L(F1;U1).                             (A2)

Corollary 2. [2, Ch. 3] Let the conditions of Theorem 5 be satisfied, then

(i) the operators S = Lf ¹ M 1 E C l(U 1 ) and T = M i L ^¹ E C l(F 1 ) are sectorial, moreover, a(S ) = a(T ) = a ^L (M);

U t =

F t =

e tS p = s- lim k→∞	(L -	m) 1 L k(p+1)   /	k(p+1) ,	for t E R + ,
P, for t = 0,	Г /	-1	k(p+1)	(A3)
e tT Q = s- lim k→∞	LL	- t-^M M) k(p+1)	,	for t E R + ,
Q, for t = 0 .

Therefore, if the operator M is strongly ( L, p )-sectorial for some p E { 0 } U N then the degenerate holomorphic semigroups U ^• and F ^• have the forms (A3). Let us describe the conditions under which these semigroups are positive.

Theorem 6. Let the operator M be strongly (L,p)-sectorial for some p E { 0 } U N , and the Banach space U be a Banach lattice, U = (U, || • ||u, U ₊ ). Then the following statements are equivalent.

• (i)    The operator [R ^ (M )] ^p+1 is positive for all sufficiently large p E R ₊ .

• (ii)    The degenerate holomorphic semigroup U ^• is positive.

Proof. (i) ^ (ii) follows from (A3). (ii) ^ (i) can be obtained by considering the representation

p

(pL - M)-1 = —52 pqHqM-(I - Q) + (pI - S)-1Li1 Q q=0

for all p E S q (M ). Hence

[RL(M)] ^p+1 = (p l - S ) ^-p-1 P.

Now we can use the arguments of Theorem 2, i.e.

∞

• (д ! - S ) ^-1 P = I e^tsPe - ¹ dt for all д > Re a(S ) = Re a ^L (M ).

Remark 4. Theorem 6 remains true if we replace the space U (and the Banach lattice U = (U,II • « u , U ₊ )) by the space F (and the Banach lattice F = (F, «• « f , F ₊ )), the operator R L (M ) by the operator L L (M ), and the semigroup U • by the semigroup F • . The proof of this fact is left to the reader.

Example 1. Let the operators L and M be represented by square matrices of the order n . The matrix M is called L-regular if there exists the number a E C such that det (aL — M ) = 0. If the matrix M is L-regular, then there exist the non-degenerate matrices A and B of the order n such that [13, Ch. 12]

L = Bdiag J, J,..., J, I n—m } A, M = B diag { I m , S } A,

o where Jpk is a Jordan box of the order pk with zeros on the main diagonal, Ik is the identity l matrix of the order k, S is a square matrix of the order n — m, 22 Pk = m. For the fixed k=1

p = max P k , the L-regular matrix M is called (L,p)-regular.

k=1,l

Therefore, let the matrix M be (L,p)-regular for some p E { 0 } U N . Since the L-spectrum a ^L (M ) of the matrix M consists of the roots of the polynomial det (дL — M ) ^-1 = 0, then the formula

U1 = У RL(M)e1t dд = A-1 diag {Om,etS}A, γ where the contour y C C bounds the domain containing aL (M), Om is the zero matrix of the order m, which defines the degenerate holomorphic group U• . According to Theorem 6, the group U• is positive exactly when the matrix

[RL(M)]p+1 = A-1diag {Om, (д! — S)-p-1}A is positive for all sufficiently large д E R+.

Example 2. Let B = (B, « • « b , C) be a Banach lattice, V • be a positive degenerate holomorphic semigroup of operators, im V • be an image of V • , and V ⁰ be the unit of V • . It is easy to see that im V • П C = { 0 } . Let us show that the inverse proposition is not true.

Let U = R ³ , the operators L and M be given by the matrices

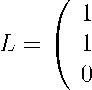
1 0 \             / 0 1 0 \

1 0 and M =   1 0 0   .

11        001

Since the L-spectrum of the matrix M is a ^L (M ) = regular and

{2

, then the matrix M is ( L, 0)-

/ 110

RL (M ) = (2д — 1)-1    1   10

у 1    i

\ 1—11

Hence t / 1  10 \ et

U t = -   1  10

• ² \ -1 1 2 /

3.    Positive Solutions to Abstract Equations

and im U • = { u E R ³ : u 1 = u ₂ } . Consider the canonical cone C = ( R + ) ³ in R ³ . Obviously, im U • П C = { u E C : u 1 = u ₂ } = { 0 } , however, the group U • is not positive. In addition, the right L-resolvent R L (M ) of the matrix M is not positive for all sufficiently large µ ∈ R + .

Let U, F be Banach spaces, the operators L E L (U; F) and M E C l(U; F). Consider linear homogeneous Sobolev type equation (2). The vector function u E C 1 ( R + ; U) is called a solution to equation (2), if the function u satisfies this equation. The solution u = u(t) to equation (2) is called a solution to problem (2), (3) if condition (3) is satisfied for some u 0 ∈ U.

Definition 10. [2, Ch. 3] The set P is called the phase space of equation (2), if

• (i)    any solution u = u(t) to equation (2) belongs to P , i.e. u(t) E P for any t E R ₊ , (ii) there exists a unique solution to problem (2), (3) for any u 0 ∈ P .

Theorem 7. [2, Ch. 3] Let the operator M be strongly (L,p)-sectorial for somep E { 0 }U N . Then the phase space of equation (2) is the subspace U ¹ .

Note that if u = u(t) is a solution to problem (2), (3) under the conditions of Theorem 7 and some u ₀ E U ¹ , then the solution has the form u(t) = U t u ₀ , where U • = { U t : t ∈ R } is a degenerate holomorphic semigroup of operators from Lemma 1. Further, if U = (U, II • llu, U + ) is a Banach lattice, and U • is a positive degenerate holomorphic semigroup of operators, then U + П U ¹ = { 0 } . Indeed, (u E U ¹ ) О (Pu = u), where the projector P is the unit of the semigroup U ^• . Since the semigroup U ^• is positive, then we have U t u ₀ >  0 for any u ₀ E U + . If u ₀ E U + П U ¹ , then (U t u ₀ >  0) ^ (Pu ₀ >  0). Denote U ¹ ₊ = U + П U ¹ .

Corollary 3. Let the conditions of Theorem 7 be satisfied and suppose that the degenerate holomorphic semigroup of operators U ^• is positive. Then there exists the unique positive solution to problem (2), (3) for any u 0 ∈ U ¹ ₊ .

The proof of Corollary 3 is left to the reader.

Remark 5. Let us show that, for any u 0 ∈ U, there exists a solution to problem (2), (4), which has the form u(t) = U t u ₀ . Since U t = PU t = U t P , then PU t u ₀ = U t Pu ₀ ^ Pu ₀ for t ^ 0+. The result follows from Theorem 7. If the degenerate holomorphic semigroup U • is positive, and u ₀ E U + , then the solution u(t) = U t u ₀ to problem (2), (4) is positive.

Now, consider linear unhomogeneous Sobolev type equation (1). The vector function u E C ¹ ((0, т ); U) is called a solution to equation (1), if the function u satisfies the equation for some т E R ₊ and f : (0, т) ^ F. The solution u = u(t) to equation (1) is called a solution to problem (1), (3) ( problem (1), (4)), if the solution satisfies condition (3) (condition (4)) for some u 0 ∈ U.

Theorem 8. [2, Ch. 3] Let the operator M be strongly (L,p)-sectorial for some p E {0} U N. Then for any vector u° E U and any vector function f : (0,t) ^ F such that f0 = (I — Q)f E Cp+1((0,t); F0) and f1 = Qf E C([0,t]; F1) there exists a unique solution u = u(t) to problem (1), (4), and the solution has the form p         q f0t

u(t) = — £ H ^q Mo¹ f (t) + U t U 0 +    u ^t-s L^f ¹ (s)ds, t E (0 ,t ).

q=°o

In addition, if the initial vector u ₀ satisfies the relation

0°

(I — Q)u° = — to £ HqM-1-f(t), t '°^~ q=0

then there exists a unique solution u = u(t) to problem (1), (3), and the solution has the form (6) .

Definition 11. Let the operator M be strongly (L,p)-sectorial for some p E { 0 } U N . The Banach lattices U = (U, || • ||u, U ₊ )) and F = (F, || • ||f , F ₊ )) are called concordant with respect to the pair (L,M ) (briefly, (L, M)-concordant) if

• (i)    U + = U ^k П U ₊ and F ++ = F ^k П F ₊ are the proper generative cones, k = 0,1,

• (ii)    the operators L E C ( U + ; F ++ ) and M E C l(U + ; F ++ ), moreover, there exist the operators L ^— E L (F + ; U ++ ) and M °1 E L (F + ; U + ).

Corollary 4. Let the operator M be strongly (L,p)-sectorial for some p E { 0 } U N , the Banach lattices U = (U, || • ||u , U ₊ )) and F = (F, || • ||F, F ₊ )) be (L,M)-concordant, and the degenerate holomorphic semigroup of operators U ^• be positive. Then for any vector function f : (0 ,t ) ^ F such that — df E C ((0 ,t ); F ++ ), q = 1,p, and f ¹ = C ([0 ,t ]; F ++ ), and for any vector u ° E U + there exists a unique positive solution to problem (1), (4), and the solution has the form (6). If, in addition, the initial vector u ° E U ₊ satisfies condition (7) , then there exists a unique positive solution to problem (1), (3), and the solution has the form (6) .

In order to prove, we note that the operator H = M ^—1 L ° E L (U + ) and, therefore, the operator H is positive.

Example 3. Let the spaces U = F = R ⁿ and the operators L,M E L (U; F) be given by the matrices

L = diag { J p i , J p 2 ,..., J _{P l} , I n-m } , M = diag { I m ,S } ,

o where Jpk is a Jordan box of the order pk with zeros on the main diagonal, Ik is the l identity matrix of the order k, S is a square matrix of the order n — m, ^2 pk = m. Fix k=1

p = max { p i ,p 2 , ...,p _k } , then the matrix M is (L,p)-regular according to Example 1.

Let us construct positive solutions to problem (1), (4). According to Corollary 4, it is necessary to show that the operator M is strongly (L,p)-sectorial for some p E {0} U N. To this end, we use equivalent conditions (A1), (A2), which are easier to verify in our case. Construct the projectors P = Q = diag {Om, In-m}. Define the subspaces U° = span {e1, e2,..., em} and U1 = span {em+1 ,em+2, ...,en}. Here ek E Rn, where the k-th coordinate equals 1, while all the rest coordinates are zeroes. Then the space U can be represented as the direct sum of two subspaces U = Uo ф U1. Similarly, we can construct a splitting of the space F. Therefore, condition (A1) is satisfied. The actions of the operators L and M are splitted and their restrictions to the subspaces Uk, k = 0,1 take the form

L o = diag J, J _P 2 , ..., ^, O n-m } , L 1 = diag { O m , I n-m } ,

M o = diag { I m , O n - m } , M l = diag { O m , S } .

Then there exist the operators

L-1 = diag {Om, In-m}, Mo-1 = diag {Im, On-m} and condition (A2) is satisfied. Therefore, we see that conditions (A1), (A2) are satisfied. Hence, the operator M is strongly (L, p)-sectorial. Construct the operator

H = M o^-1 L o = diag { J Op i , op. ,..., °_Pl , On - m } .

The formula

Ut = У RL (M )ept d^ = diag {Om,etS } γ defines a degenerate holomorphic group of operators, where the contour y C C bounds the domain containing aL(M), and Om is the zero matrix of the order m. Moreover, Theorem 6 shows that the group U• is positive exactly when the matrix

[RL(M)]p+1 = diag {Om, И — S)-P-1} is positive for all sufficiently large m € R+. Further, we assume that the matrix S satisfies this condition.

As a cone, we consider the proper cones U ₊ = F ₊ = { R ₊ } ⁿ . Then the Banach lattices U = (U, || • ||u , U ₊ )) and F = (F, || • ||f , F + )) are (L, M)-concordant. Therefore, all the conditions of Corollary 4 are satisfied. Hence, there exists a unique positive solution to problem (1), (4), which is given by formula (6) for any vector function f : (0 ,t ) ^ F such that — df € C ((0 ,t ); F + ), q = 1,p, and f ¹ = C ([0 ,t ]; F + ), and for any vector u _o € U ₊ . Note that the conditions on the vector function f : (0 ,t ) ^ F can be satisfied [10], for example, if we consider the vector function f (t) = e at f ^o , where a € R ₊ , — f ^o € F ^ .

4.    One Concrete Interpretation of Abstract Equation

Consider the monotonically increasing sequence { A k } C R ₊ such that lim A k = +to . k→∞

Construct Sobolev spaces of sequences l m , m € R , q € [1, +to) , which are Banach spaces endowed with the norm

∞ mq      q k^ Ak2 |uk / .

Obviously, the embeddings l m ^ l n are dense and continuous for all m >  n and q € [1, to) . Suppose that the operator Ли = (A 1 U 1 , A ₂ u ₂ , •••) acts in the space of sequences, then

Л : l m+² ^ l m is linear, continuous and continuous invertible for all m E R and q E [1, to) r _k                                  s _k

[8,9]. Let Lj(Z) = 52 ajZj and Mk(Z) = 52 bjZj be polynomials of the degrees rk and sk, j=o                      j=o respectively, with real coefficients such that the roots of a finite number of the polynomials Lk (Z) are the numbers Z = Aj • Construct the operators

L = diag{Lj(Aj)}, M = diag{Mj(Aj)} acting in the Banach spaces of sequences satisfying the conditions rk < sk for all k E N.                                  (8)

Suppose that there exists s = max { s _j } , denote r = max { r _j } and construct the operators L E C (lm+^T ; l m ), M E C flm ^²⁸ ; l m ). By virtue of condition (8), we obtain that s > r. Set U = l m^+2r , F = l m , m E R , q E [1, +to) , then the operators L E L (U; F), M E C l( U ; F), domM = l m^+2s .

Proposition 1. Suppose that condition (8) is satisfied and the polynomials Lk = Lk (Z) and Mk = Mk (Z) for all k E N have only real roots and do not have common roots, moreover, the roots of a finite number of the polynomials Lk (Z) are the numbers Z = Aj and the condition a^k • bjk < 0 for all k E N such that Lk(Ak) = 0                  (9)

is satisfied. Then the operator M is (L, 0)-sectorial.

Proof. Construct the L-spectrum of the operator M aL(M) = {^j E C : Цк = ^ /, k : Lj(Aj) = 0}, Lk (Aj)

where the numbers ц _к E a ^L (M ) ordered taking into account their multiplicities are real numbers and, by condition (8), tend to -to . Denote a = maxц _к . Denote by { e _j : e _j = k

(0,..., 0,1, 0,...) } a family of vectors, where the unit is on the k-th position, and construct the operator

R L (M) = ^y ' ( L j ^{( A} j ) < ^Ae j >  A e = ^y ' ( ^д j=1 ULj ^{( A} j ) - M j ^{( A} j )/ ^k j=1 V

< • , e j >

ц — ^ j

e k ,

where / at the sum means absence of the terms with the numbers k such that L _j (A _j ) = 0. Next, consider

OO I            I q 11 11 q                 CO                             m+2r

¹ L(MA->i\\^q           ^ ' |<^u’^e k >| ^e k H q,m+2r _ ^ ' |k>|^q(Ak)q ²

' ^ (M )UVq,m+2r                 l^-^k |q                        l^-^k |q j=1                      j=1

O /       m +2r \ ^q O /

_ ^ ' / |ukK^A k ) ² I ^ 'I

= h I l^-^k l -^ I j=1                    j=1

^O              m +2 r 4

= . У ' |ujI (Aj)= j=1

m +2 r

^|u k ^|(A k )     ²

sin 0|^—a|

=

sin9|^-a| q llu ^ q,m+2r ,

where the angle 6 = П2 + a, a E (0, П2 )• Therefore, we see that the operator M is (L, 0)-

sectorial.

□

Construct the splitting of the space U into the direct sum of two subspaces:

0    ?m+2r ) „ Л    ?m+2r uk = 0, k • Lk (Xk)

U = ks  = iu = {u‘}e'q    : ub = 0, k• Lt(x,) = op

<< 1    7m+2r    J       r l c 7m+2r .  uk    0,  k • Lk (Xk)    0,1

U = ‘^  = Г = {u‘}e'q   • ub = o, k• Lt(x,) = op

Similarly, we construct the splitting of the space F into the direct sum of two subspaces:

0 _ zm _ Jr _ J f \ ci 7m ■  fk = 0,  k : Lk (Xk)   0,1

F = 'q0 = U = Ш}G 'q • fk = 0, k • Lk(Xk) = 0J,

F ¹ = ' m = If = { f k } e ' m

f k = 0 , k • L k ^• f k = 0 , k • L k

(X k ) = 0/

(X k ) = 0 /

Then the operators L 1 e L (U 1 ; F ¹ ), L_T ¹ e L (F / U ¹ ), M ₀ ¹ e L (F ⁰ ; U ⁰ ) are defined as follows:

^                                    ^     «1

Lru1 = E ‘Lk(Xk) < u1, ek > ek,  Lp1 f1 = E ‘ —ek, k=1                                        k=1   Lk(Xk)

M i-"¹ / ⁰ =    E

^k: L k (^ k )⁼⁰

< f ⁰ ,e k >

M k (X k ) e k

Therefore, we see that, under the conditions of Proposition 1, the operator M is (L, 0)-sectorial and conditions (A1), (A2) are satisfied.

In the space U, consider the family of vectors { e _k } and the canonical cone U ₊ formed as a closure of a linear combination of the vectors { e _k } with non-negative coefficients. Then the space (U, U ₊ , || • ||_q ,_m+2r ) forms a Banach lattice. Similarly, in the space F, we consider the family of vectors { e _k } and the canonical cone F ₊ as a closure of a linear combination of the vectors { e _k } with non-negative coefficients. Then the space (F, F ₊ , || • | q ,m ) forms a Banach lattice. Here the sets are as follows:

<<0    ;m+2r    J      J A c ;m+2r .  uk > 0,  k • Lk (Xk)    0,1

U+ = 'q, 0 = V = {uk }G 'q • uk = 0, k • Lk (Xk ) = 0/,

1     im+2r    ) „     ( „ \ zm+2r    uk    0,  k • Lk (Xk)    0,1

^U + = ' q1   = l^u = ^{{ u k }e} ' q    • u k >  0, k • L, (X k ) = 0 p

0 _ m             f \   m   fk > 0, k • Lk (Xk)   0,1

F+ = 'q,0 = If = {fk} e 'q •  fk = 0, k • Lk(Xk) = 0  J,

1 _ im _ Jr   J f \   m   fk   0,  k • Lk (Xk)   0,1

F+ = 'q,1 = If = {fk} e 'q •  fk > 0,  k • Lk(Xk) = 0  J•

Therefore, it follows from the construction of the operators L 1 , L 0 , L ₁ ¹ , M ₀ ^-1 that the Banach lattices U = (U, || • /, U ₊ )) and F = (F, || • | f , F ₊ )) are (L, M)-concordant.

Theorem 9. Suppose that the conditions of Proposition 1 are satisfied, the values of the polynomials L _k = L _k (Z) and M _k = M _k (Z) are positive for Z = X _k such that L _k (X _k ) = 0. Then for any vector function f • (0 ,t ) ^ F such that — f ⁰ e C ¹ ((0 ,t ); F j ), f ¹ e

C ((0,т); F + ) and for any u ° E U such that u ° G U 1+ , there exists the unique positive solution u = u(t) to problem (1), (4), and the solution can be represented as

t

u(t) =

- M O ^{1 f} °М + ^U t ^u 0 +

j e ^(t-s)S Lf ¹ f ¹ (s)ds, 0

where

∞

Ut u° = 5Z‘ exp k=1

/ Mk (A k ) A \ L k ^(A k ) /

< u ° ,e k >e k .

Proof. Let us show that the operator M is positive and strongly (L, 0)-sectorial. Consider the L -resolvent of the operator M

(^L — M ) ^-1

∞

=E ‘ k=1

< • , e k >

^L k ^(A k ) ^— M k ^(A k )

) e k = E'( k=1

< • , e k >  L k ^{( A} k ⁾⁽^ ^— ^ k )

)

^e k ^,

which is a positive operator by construction. Here / at the sum means absence of the terms with the numbers k : L _k (A _k ) = 0. Therefore, we see that the operator M is (L, 0)-sectorial, conditions (A1), (A2) are satisfied, and the Banach lattices U = (U, || • ||u ,U ₊ )) and F = (F, || • |f , F + )) are (L, M )-concordant. The proof of the theorem is true by virtue of Corollary 4.

□Conclusion

In this paper, we find conditions under which a resolving semigroup of operators is positive, and obtain sufficient conditions for the existence of positive solutions to both the Cauchy problem and the Showalter–Sidorov problem for an abstract linear Sobolev type equation in the case of a relatively sectorial operator. Abstract results are illustrated by finite-dimensional and infinite-dimensional problems.

Recently, the attention of many researchers is given to the search for positive solutions. Note an interesting approach based on the Stampacchia maximum principle [14], which is applied to stochastic partial differential equations presented in the Ito–Stratanovich– Skorokhod form. The obtained abstract results are applied to the stochastic Boussinesq temperature equation and the reaction-diffusion equations perturbed by non-Lipschitz nonlinear noise. As a result, the theorems on the stability of positive solutions to these equations are obtained. Another approach to the study of stochastic equations is based on the Nelson–Gliklikh derivative of stochastic processes [15–18]. In the future, we hope to extend this approach to the study of the stability of positive solutions to linear and nonlinear Sobolev type equations.