Post-craniectomy Intracranial Pressure Dynamics:A Novel Compartmental Model of Generalized Monro-Kellie Principle

Study on intracranial hydrodynamics is needed to discover and evaluate treatment to brain diseases such as hydrocephalus, stroke, tumor and etc. A traumatic brain injury (TBI) usually causes a prompt increase in pressure of CSF compartment and, in return, over-elevated intracranial (ICP), the hydraulic pressure of cerebrospinal fluid (CSF), has been regarded as the most sensitive predictor of further intracranial deterioration after severe TBI [1]. Thus controlling the dynamics of ICP is one of the essential approaches for clinicians to manage severe head injuries. Due to its statistically significant efficacy, decompressive craniectomy (DC) is receiving increasing attention compared to other clinical surgeries. In area of the computer model simulation,

intensive works have been done on building mathematical models to describe and mimic the process of blood and CSF circulation and dynamics. In 1973 Maumarou [2] developed an original mathematical model for CSF pressure dynamics. Due to insignificant pressure gradient between the ventricles and subarachnoid space, he simply used a single compartment to represent the CSF circulation. Then the pressure volume index (PVI) was defined in animal experiments [3]. The first comprehensive intracranial simulation model was provided by Hoffman [4] with graphics rather than formula. After that most part of contribution to modeling came from the research group led by Ursino. Ursino [5] developed a novel mathematical model, which describes the quantitative interactions of different intracranial compartments. Without reducing the simulation effectiveness, Ursino and Lodi [6] offered a simplified simulation model for more practical uses. On specific areas researchers have developedbinsights on different biological parts including human intracranial biomechanical parameters, cerebrovascular autoregulation mechanism, pressure volume index [7-14] etc.

In area of clinical neurology DC is a conventional surgery to control elevated intracranial pressure, especially in TBI. But few standardized predictors for assessment of the post-craniectomy ICP waveform have been reported. Thus it is important to describe the change of ICP through DC and to provide a valuable reference for clinical treatment. However, few applications of Ursino’s compartmental model to this problem have been reported. Since Ursino gives a numerical simulation from the pathological view and provides further insights for ICP dynamics, building correspondent compartmental models for post-craniectomy ICP dynamics is a significant research direction.

This paper takes the factor influenced by DC into account, builds a post-craniectomy compartmental model, and presents the mathematical relationship between carotid arterial pressure and intracranial pressure. The remaining part of the paper is organized as follows: In section 2, the Ursino’s compartmental model is simply restated to establish a background for our further modeling. Then in section 3 an original unified framework based on DC is proposed. An additional segment—craniectomy distensible compartment is added into conventional model and the volume is computed with deflection solution. In section 4, simulation criteria and methodology is presented and the numerical results will display the clinical function of DC.

2.    Closed Cranium Simulation In most of previous studies, the lumped-paramter compartmental models treat intracranial system as a closed compartment (referred as Monro-Kellie principle). Different compartments have unified biological parameters. In 1988 Mauro Ursino [5] developed an original mathematical model of human intracranial hydrodynamics based on the hypothesis—all the elastic brain compartments are confined in a rigid skull: Va + Vv + VCSF + Vtiss — О where О is the constant volume of skull, V denotes the volume of a compartment. Subscripts a ,v ,tiss and CSF stand for arteries, veins, brain parenchyma and cerebrospinal fluid respectively. Considering the time pattern of volumes of different compartments, differentiate (1) with respect to time dVa  dVv  dVcsf  dVtiss 111= о dt    dt      dt      dt(2) Referring to previous literatures [15, 16, 17], components of ordinary differential equation (ODE) are depicted by following equations dVa              dPa ---- = mbe*(Pa Pc)() dt                   dt    dt(3) dV — о dt(4) dVCSF            Pc — Pic  Pic — Pvs dt — qf qо — Rf R0 where Pa , Pic stand for arterial pressure and intracranial pressure respectively, and m , n are constants; Pc , Pvs are capillary pressure, venous sinus pressure and Rf , R0 denote CSF formation and absorption resistances. The conservative principle of flux at the capillary implies that

P a — P c   P c — P ic   P c — P ic

---------- =--1--

R a        R f        R pv

P c —________ R f ■ R pv ■ R a ________[ P a + (— + -L) . P ic ]

R pv . R a + R f . R pv . R a + R pv . R f R a    R f   R pv

where ^Rpv , ^{R a} represent proximal venous and arterial resistances respectively. The Hagen-Pioseuille

law

shows that the lumped resistance of artery is proportional to the quartic of lumped radius of it:

R a

' k_R

^kR^Ca ² n

a

where ^{C an} is a constant ， ^Va is the arterial blood volume. Then pressure-volume relationship of brain tissue is usually considered as an exponential model:

dVic1

Ctiss —--— ------ dPic  KEPic(9)

where KE denotes the elastance coefficient of brain tissue. Equation (8) suggests that dVtiss         dPic       1

dt =   t'ss dt =  KEPic dt(10)

Combing equations from (2)—(10), we obtain a simplified version of Ursino’s model. In this paper, most of the parameters of a normal people are directly adopted from recent researches [5, 7, 8, 9, 17].

• 3.    Post-craniectomy Simulation

There are two main problems before building an analytical model for post-craniectomy ICP dynamics. First, one has to compute the craniectomy distensible volume ( Vdist ) caused by the expansion of intracranial contents showed by Fig. 1. Second, the distensible compartment should be appropriately added to compartmental model.

• A.    Distensible Voume Computation

While apply the method in [18] to compute the additional volume, the following assumptions are needed. a) Dura mater is an isotropic elastic membrane.

• b)   The part of skull removed is a rectangular bone flap.

• c)   The dura mater on the bone window after DC is an edge-clamped membrane under uniformly distributed

pressure.

Let ^{W ( x , y )} be the deflection function: the vertical displacement of point ( x , y ) of a membrane under pressure. Following expression is one of the usual forms of deflection solution of clamped rectangular membrane under uniform pressure.

д      n x       n y

W ( x , y ) —

4 P ic a (1 + cos---)(1 + cos---) ab

24 aa n ⁴ D (3 + 2- 2 + 3- 4 ) bb

where ^{P ic} is the pressure perpendicular to dura mater, ^a and ^b denote half of the length and width of craniectomy and D is bending rigidity.

D =

Eh ³

12(1 - Д ² )

E , h , ^ denote the Yong modulus, the membrane thickness and the membrane’s Poisson ratio.

Then integrate the reflection function of dura mater— ^{W (} x, y) on rectangular area S : [ - a ^, a ] ^x [ - b ^, b ] and deduce the craniectomy distension volume from it:

V dist = JJ W dxdy =

S

16 p a ⁵ b ic

24 aa ^ 4 D ⁽3 + 2 — + 3— )

bb

and

dV dist dt

dPic c - f (a,b) - dt

c = —-— where    ⁿ D

• B.    Post -craniectomy System Differential Equation

Through (3) (4) (5), one knows that the distensible volume will bring impact to every individual intracranial compartment. But the direct correlation between intracranial pressure and distensible volume suggests that the craniectomy distensible volume leads primarily to reduction of pressure in the CSF compartment (ICP) and transmits this effect to other compartments.

It is reasonable to assume that the total volume of the four compartments, after DC, is equal to the sum of craniectomy distensible volume and closed cranium volume. Thus the volume relationship is modified as

V a + V v + V CSF + V tiss = О + V dist

where V ^dist stands for the volume of craniectomy distensible compartment.

Especially the condition of ^{V dist} = 0 is correspondent to the elimination of DC factor in present model and (15) will be degenerated to the model under original Monro-Kellie principle.

Differentiating in two sides of (15) leads to dVa  dVv  dVcsf  dVtiss  dVdist

----- ^h ----- ^— -------- ^h ------- — ------- dt    dt      dt      dt      dt                                                          (16)

dVa    dVv    dVCSF  dVtiss     dVdist where the expression of dt ， dt ， dt , dt and dt have been presented by (3)-(9) in section 2

and by (14). Substitute these equations to (16) and achieve the ultimate system equations

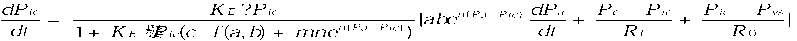
where      in (18) stands for the initial value of intracranial pressure under different pathology.

According to (17) DC factor represented by ^{f ( a , b )} can reduce the overall magnitude of ICP waveform.

• C.    Numrical Simulation

In (17) ICP is directly influenced by the size of DC bone flap and the magnitude of input arterial pressure. Thus the ICP function is written as P ic ⁽ t ) = P ic ⁽ a ^, b ^{, Pa (} t ^), t ) . In this paper we focus on the DC size factor in ICP dynamics and use the waveform of arterial pressure by referring [5].

Fig. 2 shows   the simulation results. The   values of DC size variable   are   taken as 0 x 0 , 8 x 8 , 10 x 10 , 12 x 12 , 14 x 14 and 16 x 16 square centimeters sequentially, where the size 0 x 0

corresponds to pre-craniectomy intracranial dynamics. The initial value of the (18) is set as 13 mmHg, standing for abnormality of intracranial pressure, which in fact simulates the case of a prompt traumatic brain injury.

From the simulation result DC effectively alleviates intracranial hypertension. With the increasing of DC bone flap size, the main peak , denoted by P ic , of P ic from 21.3mmHg (corresponding to 0 ^{x 0}) is reduced to 14.5mmHg (corresponding to ^{16 x 16} ). Additionally when the DC area is smaller than ^{8 x 8} square centimeters, the reduction of ICP value is restrained as shown in Fig. 3.

volume.

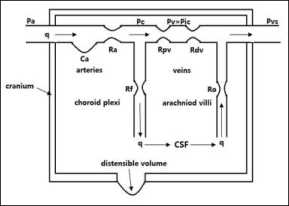
Fig 1. Hydrodynamics circulation and craniectomy distensible

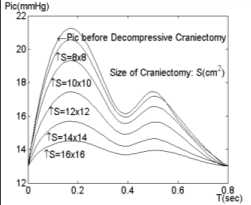
Fig 2. Waveform of ICP under different size of craniectomy

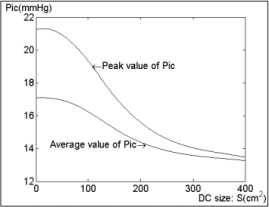
Fig 3. The peak and average ICP .vs DC. Size curve

4.    Discussion And Conclusion

To provide more suggestions for controlling the brain injury, this paper has added a decompressive craniectomy factor to the intracranial dynamics system and simulates ICP corresponding to a pulsation of the cardiac cycle with post-craniectomy model.

As a complex and clinically important pathological state, elevated intracranial pressure is most commonly due to severe TBI, brain tumors, or obstruction of cerebral spinal fluid (CSF) drainage. Thus it is significant to discover and evaluate treatments for elevated ICP in both the pre-craniectomy and post-craniectomy cases. A wide variety of mathematical models have been developed to understand the complex mechanism that drives ICP dynamics. However no literatures have reported the post-craniectomy model.

In patients with TBI a significant correlation between the size of the craniectomy and the decrease in ICP was found in [19]. This study has shown that the larger the removed bone flap is, the more the ICP is reduced, which is in line with our simulating results. Moreover, by combining with the increment volume resulted from the craniectomy, the differential (18) of the model generates a relationship between the ICP waveform and the size of craniectomy. According to the peak and average ICP .vs. DC Size curve, it is reasonable to believe that DC of craniectomy size smaller than 64 square centimeters cannot relax the raised ICP effectively and there is an interval of the size variable (about 80-200 square centimeters) that can decrease ICP significantly. Outside the interval the curve looks like a little flat, which means a smaller size cannot reduce the raised ICP effectively as well as a further improvement of the raised ICP is very limited when the size is above the up-boundary of the interval.

The work presented here is the quantitative description of the relationship occurring between ICP and CBV in the post-craniectomy case. Analysis of this relationship can be of the greatest importance in neurological practice. More comprehensive and powerful models describing specific disease mechanisms should be expected in future application of our framework.

Acknowledgment

This work is supported by National Science Foundation of China (Grants No. 60773195), the Fundamental Research Funds for the Central Universities (HUST, Grants No. 2010MS131), Science and Technology Innovation Fund for College Student (HUST, Grants No. 2010135).