Постановка и метод решения обобщенных краевых задач электро- и тепломассопереноса в катодном узле сильноточных плазменных систем

Теплофизическое состояние и уровень эрозии катодов сильноточных плазменных систем (СПС) определяют их функциональные параметры и работоспособность [1–3]. Наибольший ресурс катодов достигается в режиме термоэмиссии при использовании в качестве электродного материа- ла тугоплавких металлов, активированных легирующими компонентами из окислов редкоземельных элементов с низкой работой выхода электронов [4]. Во время работы плазменного устройства в связи с испарением и выгоранием активаторов происходит деградация физико-механических свойств материала, что приводит к снижению эксплуатационных характеристик катода. Ресурс данного класса электродов зависит от интенсивности выхода легирующего элемента из объема матрицы основного металла. Поэтому для оптимизации их функциональных режимов необходимо исследование динамики процессов электро – и тепломассопереноса в объеме и на поверхности твердого тела в зависимости от внешних параметров системы, задаваемых условиями эксперимента и практики. Именно вопрос повышения ресурса работы катодов в наибольшей степени сдерживает применение СПС в инновационных энергоемких технологиях и является одним из главных практических задач фундаментальной проблемы исследования взаимодействия низкотемпературной плазмы с токонесущей стенкой – термоэмиссионным дуговым катодом.

Постановка задачи

Электродный узел с термоэмиссионным катодом в сильноточных плазменных системах (СПС) представляют собой структуру, функционирующую в экстремальных условиях в термическом и радиационном полях большой интенсивности (10³ – 10⁵ Вт/см²). Характер теплоотвода от катода определяется особенностями конструкции электродного узла. В настоящее время в СПС ввиду конструктивной простоты и многофункциональности эксплуатационных характеристик наиболее эффективными являются составные катодные узлы, состоящие из стержневого катода – вставки I из активированного вольфрама, запрессованного в интенсивно охлаждаемую медную обойму II (рис.1). Осевая симметрия физической системы «катодный узел – дуговой разряд» обеспечивает наиболее устойчивый контакт при взаимодействии прикатодной плазмы с твердым телом. При этом катодное пятно представляет собой круг диаметром d 0 .

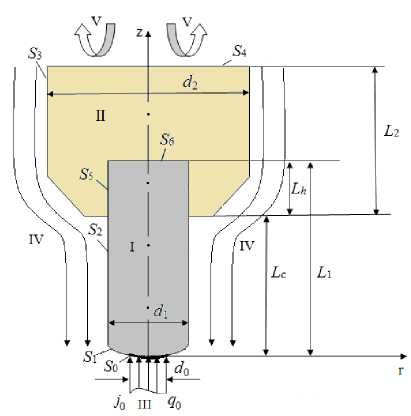
Рис. 1. Составной катодный узел плазменных устройств.

I – катод (вставка), II – корпус узла (обоймы), III – плазма разряда, IV – плазмообразующий газ, V – теплоотвод (жидкость)

На рис.1 показаны геометрические размеры осесимметричной конструкции, где S 0 – поверхность контакта "плазма – металл", S 1 – неэмиттирующий торец катода, S 2 – поверхность радиационноконвективного теплообмена катода, S 3 – поверхность конвективного теплообмена обоймы, S 4 – охлаждаемый торец обоймы, S 5 , S 6 – поверхности контакта "катод - обойма".

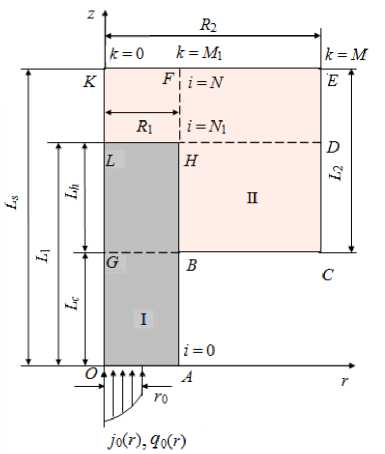
Рис. 2. Расчетная модель катодного узла.

Полуплоскость осевого сечения расчетной модели составного катодного узла представлена на рис.2. На торец стержневого катода S 1 ( r ,

0) в пределах контакта с дуговым разрядом радиуса r 0 из прикатодной плазмы поступают тепловой и электрический потоки с плотностями q 0 ( r , 0) и j 0 ( r , 0) соответственно ( r , z – цилиндрические координаты). Значения этих параметров определяются из совместного анализа процессов на поверхности металла и в прикатодной плазме [5].

Строгий подход к обобщенной задаче электро- и тепломассопереносса состоит в совместном решении уравнений математической физики эллиптического и параболического типов с краевыми условиями, адекватными условиям функционирования катодных узлов реальных плазменных устройств. Цилиндрическая симметрия рассматриваемого электродного узла позволяет трехмерные физические поля F ( x , y , z ) привести к двумерным F ( r , z ), что в значительной степени упрощает их математическое моделирование и анализ. Таким образом, задача сводится к решению трех дифференциальных уравнений с нелинейными граничными условиями в двумерном приближении:

• 1)    уравнения нестационарной теплопроводности

  д T 1 д

  P k   ' =--

  д t    r д r

  
  

  r^ (T ) ^ Tk- д r

  
  

  д

  + —

  д z

  
  

  A ( T , ) ^ + J»I a , (T , ) (1 d z

  
  

  )

  
  

• 2)    уравнения непрерывности тока (Лапласа)

  1A r д r

  
  

  r ° , ( T , ) U о r

  
  

  д

  + — д z

  
  

  ° , (T k )

  
  

  d U , д z

  
  

  = 0,

  
  
  
  

J, = (J2 + J2)1/2,     Jr = -°,(T,)ди, Idr,     jz =-°,(T,)dU, Idz для катодного узла (, = 1 - катод, , = 2 - обойма), показанного схематически на рис. 2.

• 3)    уравнения нестационарной диффузии активатора в объеме катода

  d n 1 д / \ d n     9

  ₌ _    rD ⁽ T , )     ₊

  o t r д r        д r   д z

  
  

D ( T , ) d n 1. D ( T ) = D o exp( - Q7- ),   (3)

az j                       вв,к где T, - температура; c,, р,, X,, °, - соответственно удельная теплоемкость, плотность, коэффициент теплопроводности, удельная электрическая проводимость материалов катодного узла; jk – плотность тока; Uk – потенциал электрического поля; n, D, D0, Qa, – соответственно концентрация, коэффициент диффузии, фактор диффузии, энергия активации легирующего элемента (присадки); kB – постоянная Больцмана, t – время.

Решения уравнений (1) и (2) с соответствующими граничными условиями проведены в [6, 7]. В отличие от краевых электрической и термической задач диффузионная задача ставится и решается только для катода – вставки.

Граничные условия к уравнению (3) следующие:

• 1.    В начальный момент времени концентрация присадки в катоде считается распределенной равномерно и равной

• 2.    На холодном торце катода (поверхность LH ) концентрация остается постоянной

• 3.    На поверхности горячего торца катода ( OA ) происходит испарение присадки и возврат ее из приэлектродной области в пределах контакта с разрядом – круга радиуса r 0 :

  - D ( _T ) ⁶ n ( r ,0, ¹ ) = / ⁽¹ -П ⁾⁽ n / n м^{) 2/} 3 ^{w( T} ),       ⁰ < ^r < r

• 4.    Радиальный поток активатора на оси симметрии катода ( OL ) равен

• 5.    Граничное условие на цилиндрической поверхности ( AH )

n ( r , z ,0) = n 0

n ( r , L 1 , t ) = n 0 ,       0 <  r <  R 1

dz      [   (n / nM)2/3w(T),         r0 < r < Ri где nм – концентрация частиц основного металла в катоде; коэффициент (n/nм)2/3 учитывает различие поверхностных и объемных концентраций присадки; n — доля ее атомов, возвратившихся на поверхность катода за счет рециклинга из приэлектродной области; w(T) – скорость испарения присадки (частиц/м2-с).

нулю

⁸ n ⁽⁰-' t ) = 0,                0 < z < L 1

d z

• - D(_T ) ^{d n (} R ^1, z , t ) = ( n / n м )^2/ 3 w( _T ),         0 <  z <  L c ,

о r dn(R1, z, t) = 0, Lc < z < L1 dr

Граничное условие в месте контакта дугового разряда с катодом отражает уникальное явление – ионно-атомный рециклинг в прикатодной плазме [1]. Испарившиеся атомы металла, попадая в приэлектродную область, легко ионизируются электронами, так как вероятность ионизации металла больше вероятности ионизации рабочего газа. Соотношение p / а ~ n ° / n 0 ( p , a - скорости ионизации и рекомбинации;

n_e ⁰ , n_a ⁰ – равновесные концентрации электронов и атомов соответственно) больше для металла с меньшим V i , что приводит к увеличению скорости избыточной ионизации атомов присадки по сравнению с атомами основного металла и рабочего газа. Под действием электрического поля ионы материала катода возвращаются обратно на поверхность, где восстанавливаются до атома. В результате этого скорость испарения и удельная эрозия катода в области пятна получаются значительно ниже рассчитанных по температуре поверхности.

Скорость испарения в вакууме рассчитывается по известной ленгмюровской формуле

w( T ) = Рн41/(2 п MRT) ,                 (4)

где P н – давление насыщенных паров; М – молярная масса.

При испарении в газовой среде выражение (4) записывается в виде:

w(T) = aPpJ1/(2nMRT) , где aP - коэффициент испарения (Ленгмюра), который зависит от рельефа и чистоты поверхности катода, давления и рода рабочего газа.

Метод решения

Уравнение диффузии (3) в рассмотренной выше постановке аналитически не решается, так как является квазилинейным уравнением с переменными коэффициентами. Поэтому для численного решения применяем локально-одномерную схему прогонки метода конечных разностей [8]. Чтобы обойти трудности, связанные с выбором системы единиц измерения, а также в целях универсализации решения исходное уравнение приводим к безразмерному виду:

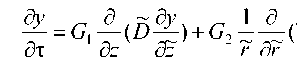
У = n / n o, t = t / To,

D = exp( - Q / kT )   (5)

где

~ = z / L 1 ,     r = r / R 1 ,

~

D = D / D 0 ,

G 1 = D 0 ^T 0 / L 1 ,    G 2 = D 0 ^T 0 / R 1 .

Остановимся на некоторых особенностях поставленной задачи. В данном случае использование явных схем нецелесообразно, так как D(T) является быстроменяющейся функцией и условие устойчивости таких схем t < h2 / 2maxD(T) требует очень малого шага т по времени. Поэтому расчет необходимо вести по безусловно устойчивым неявным схемам с весом 8 > 0,5 [8]. Используя пространственно-временную сетку, введенную при решении электрической и тепловой задач [6, 7], с учетом переменности коэффициента D (T), производные уравнения аппроксимируем следующим образом (знак «тильда» для упрощения опускаем):

^yJj, + 1 - y^Jj, k

д

5z

1 д r д г

1 h ₂ / R

D

D

\

+

-1 V

+      ⁽ D k - 1/2 "  y r , k + D k + 1/2 "  y r , k ):

2 r_k                 ^{,                    ,}

Ук -Ук-1                                                  .

где y_{F k} =--левая разностная производная в точке yk ;

^{r , k}     h ₂ / R ₁

Ук+ 1- У к

У г к = ^—~---~ — правая разностная производная в точке у_к .

r , k      h ₂ / R ₁

Коэффициенты

D ( i , k ) – 1/2 = D ( x i , k – 0,5 h 1,2 ), D ( i , k ) + 1/2 = D ( x i , k + 0,5 h 1,2 ) выбираются из условий второго порядка аппроксимации на полушаге пространственной сетки в точках ( x i , k – 0,5 h 1,2 ) и ( x i , k + 0,5 h 1,2 ) соответственно. Это позволяет устранить немонотонность в решении сеточных функций, появляющихся при использовании полных шагов на пространственной сетке. Применяемая схема является абсолютно устойчивой, монотонной, непрерывно дифференцируемой и имеет погрешность аппроксимации 0 ( т + h 2 ).

Уравнение (5) в разностном виде запишется:

y j ^{+ 1} - y j = G [ d , + 1/2 ( y j + - y j ^{+ 1}) - D , -_ш ( y j + - y j ^{+ 1}) ] /( h 1 / / ) +

+ G 2 [ D k + 1/2 < y k + 1 - y j ^{+ 1}) - D k - 1/2 ( У    - y k +Dk h 2 / R 1 ) 2 +             (6)

G 2

⁺ „    ⁽ D k - 1/2 ' ^yr , k ⁺ D k + 1/2 ' ^yr , k )•

2 r_k

Применяя локально-одномерную схему, вместо уравнения (6) последовательно решаем одномерные задачи с соответствующими граничными условиями yj+1 -yj = G1 [D,+1/2(y    -yj+1)-D,-1/2(yj+1 -y/-+1)]/(h1// > (7)

y k ^{+ 1} - y k = G 2 [ D k + 1/2 ( y k ^ ¹ - y k ^{+ 1}) - D k - 1/2 ( y k ^{+ 1} - y k + 1 ) ] /( h 2 / R 1 )² +

G ₂

7;   ^{( D} k - 1/2 ' ^y r , k ^{+ D} k + 1/2 ' ^y r , k )

^{2 rk}                                                                       (8)

соответственно по координатам z и r .

Расчет по координате z

После несложных преобразований уравнения (7) имеем:

D , - 1/2 • y j + - ( D , - 1/2 + D , + 1/2 + 1/ N ² G 1 ) y j ^{+ 1} + D , - 1/2 у , + 1 = y j /( N 2 G 1 ) Обозначив

4 = D - 1/2 , B , = D + 1/2 , C , = D , - 1/2 + D , + 1/2 + 1/( N ² G 1 ), F , = У / /( N 2 G 1 ), получим разностное уравнение вида:

АУ + - cy ^{+ 1} + В , У ^ =- F •

Решение системы алгебраических уравнений такого типа подробно рассмотрено в предыдущей главе. Здесь остановимся на деталях аппроксимации граничных условий данной задачи.

После обезразмеривания граничное условие на рабочем торце электрода в разностном виде запишется следующим образом:

—

y N ^j

—

h ₂ / L ₁

y^jN — 1 _{= <}

—

^{(1 —} n ^)w0 L i^{w( N} , k ) "  y N + 1/3 2/3               j 1/3

D 0 n 0 n м D N — 1/2 ^{( y} N )

W ) L i w( N , k ) " y j ^{+ 1}

1/3 2/3               j 1/3 ,

D 0 n 0 n м D N — 1/2 ^{( y} N )

, 0 <  r <  r ₀

^r o <  ^r <  R i

Подставив y N + l = a _Ny^J_N + 1 + P _N в уравнение, концентрации y_N^j на новом временном слое:

^{(1 —} p ) d n — 1/2 " P n

находим значение

v j+1 = ^

yN =

(1 — a n ) D n — 1/2 + P w( N , k )/( y N )^1/3

D N — 1/2 " P N

, 0 <  r <  r ₀,

. (1 — a N ) D n — 1/2 + P 1 W( N , k )/( y N )^1/3

, Г ) <  r <  R 1 ,

где P 1 = w 0 h 1 /( D 0 n 0 ^1/3 n м ^2/3) – безразмерный параметр; w 0 – скорость испарения присадки при температуре Т 0 .

Расчет по координате r

Подставляя в уравнение (8) выражения соответствующих производных из (6), получим j+1 vj —    G 2     Гг)     (vj+1 ,,j+Ц П     ( tj+1 vj+Ь11 I yk — yk =         2 [Dk+1/2(yk+1 — yk ) — Dk—1/2(yk — yk—1)] +

( h ₂ / R ₁ )

।__G 2_______ Гг)       ^j..,j ⁺¹ _ ... j ⁺Ц_|_г)       ^j-.,j ⁺¹ _ ,, ^{j +}ц1

+         / D A2 ^[ D k — 1/2⁽ y k      y k — 1 ) ⁺ D k + 1/2⁽ y k + 1 y k ^{) ]}

2 k ( h ₂ / R ₁ )

С учетом соотношения M 2 = 1/(h2/R1)2 имеем yj+1 — yj = G^M2 {Dk+1 /2( yjt1 — yj+1) — Dk_x/2 (yj+1 — yj+1) + k k          2          k +1/ 2 k +1      k           k 1/ 2 k k 1

+ :1 [ D -i /2 ( y j + 1 — y j + 1 ) + Dk₊i /2 ( y j + 1 — y j + 1 )]}

7 L k 1/ 2 x v к к —1 l /       к + 1/ 2 x •/ к + 1 v к z

Раскрывая скобки, приведя подобные члены и обозначив A k = (2 k – 1) D k -1/2 , B k = (2 k + 1) D k +1/2 , C k = (2 k + 1) D k +1/2 + (2 k – 1) D k –1/2 + 2 k /( G 2 M ²), F k = 2 ky k ^j /( G 2 M ²) , M = R 1 / h 2

получим систему разностных уравнений для значения искомой функции y k на новом временном слое t = t ^{j +1}

АкУГД — Ckyk+1 + Bkyk+11 = —Fk ,0 < k < M где Fk – известная функция, определяемая по значениям функции на предыдущем слое .

На внутренней границе (k=0) определяются начальные прогоночные коэффициенты a и pi. Так как на оси симметрии радиальный поток _ „     „   _ „              „ 1 d z п dnA            _ равен нулю, в уравнении диффузии член--(rD —) при r^0 является r dr    д r неопределенностью типа 0/0. Раскрывая эту неопределенность 109

1 d     dn       d 2 n lim (rD —) = 2 D—-r^o r dr    dr       5r2

на оси симметрии для прогонки по r получаем следующее разностное уравнение:

y + - y 0 = 2 G 2 D _0+ш( y -+ ¹ - 2 y ⁺ - y r ¹) ( h 2 / R J²

Поскольку y-"+1 = y j+1, получим y - y 0= 4 M2 G 2 D 0+1/2( y + - y 0+1)

Сравнивая с y 0 ^{1 1} = a 1 y j" ^{+ 1} + p 1 , находим

« 1 = 4 M ² G 2 D 0 + 1/2 /(1 + 4 M ² G 2 D 0 + 1/2 ), p , = y 0 /(1 + 4 M ² G 2 D 0 + 1/2 )

Краевое условие на цилиндрической поверхности в разностном виде запишется как yM+1 -yM+-1 =   w0R1   x w(M,z)yM+1 r = R h 2/ R1     D 0 n 0/3 nM3 Dm_ш( yM )1/3,     1, yM-1 = a MyM + PM

Исключая yM1, находим граничное значение искомой функции j+1 =_______________DM-1/2 " РM_______________ '

M    D m - 1/2 (1 - a m ) + P 2 w( M , z )/( y M )^1/3

с обозначениями

P 2 = ^W0 h 2^{/( D} 0 n 0 n м ), ^D M - 1/2 = ^{( D} M ^{- D} M - 1^)/2.

При прогонке по локально-одномерной схеме разностные уравнения (7) и (8) преобразуем к алгебраической системе вида

Ai,k y(i,k)–1 – Ci,k yi,k + Bi,k y(i,k)–1 = – Fi,k с условиями Ai,k > 0, Bi,k > 0, Ci,k > Ai,k + Bi,k разрешимости системы данным методом. Далее решение задачи находим по известной формуле:

y ( i , k ) = a ( i , k ) y ( i , k )+1 + P ( i , k )+1 , i = 0,1,2,..., N -1; k = 0,1,2,..., M -1

_       Pi,k               o _ Fi,k - Ai,kPi,k a (i, k )+l = c _ .        ,       P( i, k )+l = c

C i , k    A i , k ^a i , k                       C i , k    A i , k ^a i , k

Значения начальных прогоночных коэффициентов a 1 и р 1 определяются на внутренних граничных условиях катода. Затем из других граничных условий вычисляются значения сеточных функций y N , M и по формуле (9) – все остальные значения y ( i , k ) . Переход от времени t к t +1 реализуется через последовательное чередование прогонок по координатам z , r . В результате получается двумерное распределение концентрации активатора в объеме цилиндрического катода в зависимости от времени работы плазменного устройства.

Заключение

Математическое моделирование процессов электро- и тепломассопереноса проводится в следующей последовательности. Сначала решаются электрофизическая и термическая задачи в предположении постоянства эмиссионных характеристик катода. Затем, используя поле температур в системе «катод – обойма», решается уравнение диффузии по составленному выше алгоритму. Цикл повторяется до выхода газового разряда на стационарный режим. Численный алгоритм позволяет исследовать динамику выхода и испарения легирующей примеси из термоэмиссионных катодов плазменных устройств в широком диапазоне изменения их рабочих параметров.