Постановка математической задачи и методы решения разработки антистатической одежды для защиты от повышенных температур

Вопросы обеспечения электростатической безопасности определяются вариантом состава и параметрами материалов. Совокупность этих взаимозависимых характеристик является входной информацией для выполнения инженерных расчетов в области конструирования одежды.

Основы математического моделирования определяются первоначально представлениями процесса электризации текстильных материалов в рамках системы «Человек - Одежда - Среда». Явление статической электризации, возникающее в процессах изготовления текстильных материалов и изделий из них, а также при эксплуатации готовых изделий, ведет к снижению качества продукции, доставляет неудобства в работе, нарушает технологические процессы производства, а при возникновении электрического разряда представляет угрозу человеку и может приводить к несчастным случаям.

Модели, описывающие процесс возникновения электрического заряда, его влияние на производственный процесс и на организм человека, рассматривались в работах исследователей [1-10]. Автор [1] отмечает трудность интерпретации и сопоставления получаемых результатов при исследовании электризации вследствие большого разнообразия процессов взаимодействия между контактирующими материальными средами. Такие взаимодействия как трение, сжатие, растяжение, сдвиг и т.д., увеличивают площадь контакта двух сред. А в зависимости от скорости протекания этих процессов усиливают или ослабляют обменные процессы, что способствует увеличению максимальной величины статического заряда, образующегося на контактирующих поверхностях. Поэтому, механические воздействия играют большую роль в процессах электризации, что отмечают все исследователи.

Модель процесса электризации при контакте двух диэлектриков с переходом электро- тава человека в положениях стоя и сидя. Прогнозирование тепло и влагопотерь осуществляется при помощи моделирования процесса теплопередачи с поверхности сложных стенок коленного сустава, при сгибании ноги, геометрически представленной в виде цилиндра и сферы.

Работа [10] посвящена разработке математической модели воздействия ветра на пакет одежды с объемными несвязными утеплителями. Для решения этой задачи ис- нов, где рассмотрены условия перехода заряда пользована цилиндрическая модель туло- при контакте двух диэлектриков с различными энергиями уровня Ферми, рассмотрена в работе [2]. Модель процесса электризации, основанная преимущественно на диффузном переходе ионов с одной поверхности на другую, предложена в работах [3,4].

Автором [5, 6] разработана математическая модель системы «Человек-Специаль- ная защитная одежда от низких температур и статического электричества-Среда», позво- ляющая рассчитывать параметры пакета одежды с антиэлектростатическим эффектом.

Работа [7] посвящена расчету оптимальных параметров толщины теплозащитных слоев одежды на основе оптимизационной математической модели «Человек-Одежда-Среда» и обосновано, что для оптимизационного моделирования целесообразно использовать модель с «овальным» сечением туловища, так как это сводит последующие решения к осе симметричным.

В работе [8] разработана математи- ческая модель распределения температурного поля в слоях «Человек-Одежда-Среда», учитывающая зависимости деформации теплофизических и геометрических характеристик системы в процессе проникновения сырой нефти в пакет материалов одежды.

В работе [9] разработана математическая модель системы «локальная зона человека теплозащитная одежда окружающая среда», дающая возможность прогнозировать тепловое состояние коленного сус-

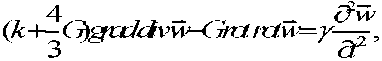
^Ө-Ц\/^—77iwi--O/ х

вища человека, покрытого равномерным слоем одежды с объемным утеплителем.

Из анализа рассмотренных моделей можно сделать вывод, что большинство моделей явления электризации, предложенных исследователями, касаются теплозащитной одежды для пониженных температур. При математическом моделировании изменения электростатического заряда во времени рассматривался только процесс стекания заряда посредством электропроводимости, а эмиссия электрического заряда с поверхности материала в воздушную прослойку и зависи -мость электрической проводимости материала от его влажности не учитывались.

Материалы и методы исследований

Исходя из вышеизложенного, основной целью данной работы является разра -ботка математической модели антистати -ческой одежды для работы в жарких климатических условиях. В этой связи тело человека рассматривается как деформируемое цилиндрическое тело конечного размера, а одежда как мягкая оболочка (рис 1) Исследуемая задача сводится к моделированию деформаций цилиндра с мягкой оболочкой. Данная постановка задачи позволяет исследовать напряженно-деформированное состояние цилиндра при тепловом воздействии с учетом влияния электростатического поля. Уравнения динамики цилиндра с тонкой скрепленной оболочкой принимает следующий вид

,    „      _           л          -7=№2/уц где: к-объемный модуль; G-модуль сдвига; Ө -температура;

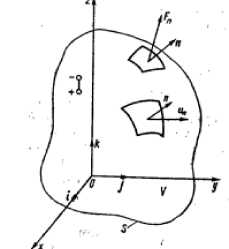
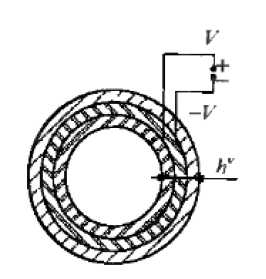
Рисунок. 1. Расчетная схема для разработки математической модели антистатической одежды:

λ и µ - коэффициенты Ламе; α -коэффициент линейного термического расширения; χ= λ/ c ; c - удельная теплоемкость при постоянной деформации; λ -постоянная величина; Q- величина, которая зависит от количества тепла; γ -плотность на единицу объема материала цилиндрического тела; w(wr, wϕ, wz) - вектор перемещений цилиндра.

Если одежда рассматривается как многослойная цилиндрическая оболочка, тогда дифференциальные уравнения оболочки записываются в виде

cf v 1—VcTv 1+v і?м 5w mH2^' ----- -I----I----1------— I

082   2 do?   2 ОаОб Од  S' OP

^M 1—V^U 1+V С? V ^^^ mb'2 ^u "Oa?^ 2 cV+ 2 ОаЗӨ+ Tl?

, ди д\' 1V7№

V=^-a=--,nl где

масса

многослойной оболочки, отнесенная к единице площади нейтральной поверхности (А); b′ -радиус нейтральной поверхности. Система уравнений (2) отличается от соответствующих уравнений оболочки только жесткостями на растяжение и изгиб. Полные уравнения движения оболочки цилиндра в цилиндрической системе координат имеет следующий вид:

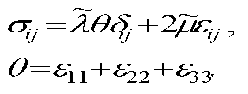
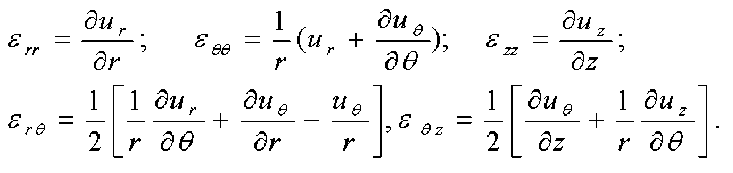
Вынужденные уравнения электростатики имеют следующий вид (рис. 2)

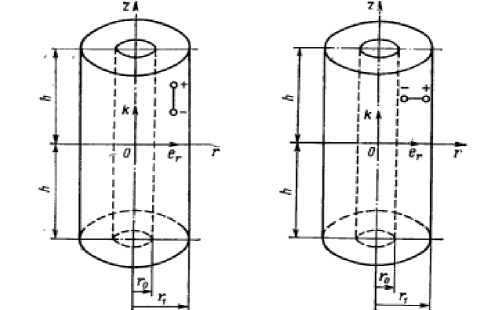
Рисунок.2. Цилиндр в электростатическом поле

Электростатическое поле учитивается через граничные условия при z= ± h , которое имеет следующий вид :

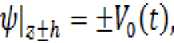
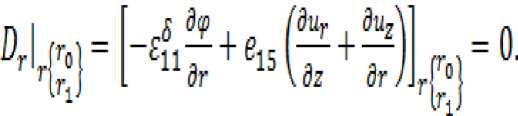
Таким образом, математическая постановка модели системы «человек-одежда-среда» дает возможность оптимального выбора определения состояния одежды при внешних воздействиях.

Методика и алгоритм решения задачи деформации одежды ограниченной длины при наличии теплового потока.

Дана одежда ограниченной длины     . Площадь поперечного сечения предполагается постоянной по длине. Модуль упругости материала одежды - E , коэффициент теплового расширения материала стержня - а. Одежда с внутренней стороны свободно держится, или оболочечный цилиндр и внутренняя полость тела имеют скользящий контакт. Вместе с этим на поверхности поперечного сечения приложен тепловой поток q(Вт / см2) . Через площадь поперечного сечения происходит теплообмен с окружающей средой. (рис. 1). Требуется по длине тела с заполнителем от поля температуры и электромагнитное поле.

Естественно, возникающие при этом поля температур, перемещений, деформаций и напряжений будут распределены по длине конструкции нелинейным образом. В связи с этим, в малой части длины конструкции, поле распределения физических величин примем в виде кривой второго порядка. Например, рассмотрим поле распределения температуры в интервале 0 <  х <  £ , где £ << L - конечная длина рассматриваемого частично теплоизолированного стержня; £ -

£ < (ОД см) длина части одежда,

Предположим, что поперечное сечение постоянно по длине стержня, тогда в интервале 0 < х < £ поле распределения температуры Т = Т(х) представим в виде кривой второго порядка, определить поле распределения температуры

, при 0 <  х < £ ,

где а,а,а - некоторые константы, значения которых пока неизвестны. Для нахождения значения этих констант, рассматриваемую часть стержня делим пополам. И в этой части фиксируем три узла        (рис.

3). Глобальные координаты этих узлов соот- ветственно          , при этом

.

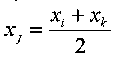
i

	—
		x
		j                      k
	l/2

Рисунок 3. Квадратичный конечный элемент с тремя узлами

При этом в местной системе координат координаты трёх узлов определяются следующим образом: х = 0;

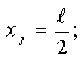
xk = ^£ .

Далее введём следующие обозначения, характеризующие значение температуры в узлах i , j , k .

Т1=Т(х = х1У Т Т(х х

У Тк=Т(х = хк)

Таким образом, для первой и второй половины стержня находим значения истинного термоупругого напряжения

45о£ 55ой ІООой

=-25ой;

45а£ 145о£ ЮОай ------------=-------=- 2 5 ой.

Полученные численные результаты (на 100% точно) совпадают с аналитическими решениями, приведенными в работах [1,2]. Эти сравнения показывают, что точность результата метода приведенного универ-

сального вычислительного алгоритма является самой высокой.

В пределах этого элемента апрокси-^тм мируя температуру          квадратным полиномом, получим следующее выражение

Г=Г(х) = ^ (х)Г, + ^ (х)^ + % (х)Тк

,

где

- функции формы

для одномерного квадратичного конечного элемента с тремя узлами, и они выражаются

через формулу (8). Тогда в пределах этого элемента градиент температуры определяется следующим образом

^=^^г+^^г+^^г

.

Как видно, здесь надо учитывать удлинение и расширение одежды  за счет

температуры.

Дана     одежда

ограниченной

кк поперечного сечения правого конца температура окружающей среды

,

.

длины     . Площадь поперечного сечения постоянна по длине. Коэффициент теплообмена с окружающей средой через площадь

Требуется определить поле распределения температуры по одежде. Расчетная схема задачи приведена ниже (рис. 4).

hk,T h,T i oci

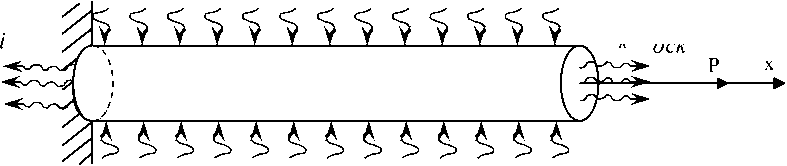
q

k

i

j

Рисунок. 4. Одежда под влиянием теплового потока и растягивающей силы

Рассмотрим данный стержень как квадратичный конечный элемент с тремя узлами .

Дифференциальное уравнение распределения температуры данного случая будет таким

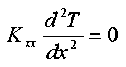
Т

Отсюда определим

Тк =

^хх^^і^осі ^кТоскУ ^^ ^Кхх*^^*^^Ч^ ^оск

(AA^+AA+W2)^

Из последней формулы видно, что на значение температуры      прямо пропорционально значению  коэффициента тепло проводности материала одежды, тепловому потоку подведенному к боковой поверхности

одежды. Теперь, подставляя найденное зна чение     в выражение (12), найдем значе- т.

ние температуры -^ в точке _x = x^ стержня

oti +^ock V^k

^оск

,           \ік-ғ<ЛтгМ*к.-ггМ*ҺіМ1')

ядгУ (ДбК^1 ^Х^К^и^К^^+ЗҺ^У)

nmK^uK^^Vb

Далее построен вычислительный алгоритм определения деформационного состояния одежды ограниченной длины при наличии теплового потока и теплообмена. Выявлен соответствующий функционал, выражающий полную тепловую энергию рассматриваемой одежды с учетом заданного теплового потока, теплообмена и растягивающей силы. Минимизируя последние по узловым значениям температур, построена разрешающая система линейных алгебраических уравнений.

Результаты и их обсуждение

Дана одежда ограниченной длины.       Площадь поперечного сечения

постоянна нец одеждs жестко конце приложена

по длине. Верхний ко-защемлен, а на нижнем осевая растягивающая

сила

стержня проводности

. Модуль упругости материала

, коэффициент тепло-

к (Вт/\.см

К_хх ,(

расширения-стержня

-

материала стержня

), коэффициент теплового

.

В

задана

верхнем конце температу-

т = ти = ^ = т, ра                     .

боковой поверхности и

Через

участки

1 — л2 — л3

площади попереч-

ного сечения нижнего конца стержня проис-

ходит теплообмен с окружающими их средами. Здесь температуры окружающей среды т т т обозначим через 1 ociVoc^ocs , а коэффициенты теплообмена с окружающей сре- дой соответственно

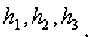
Боковая по-

верхность

0 < х < хр х2 < х < х3, х4 < х < Z теплоизолирована участков одежды

(рис.5)

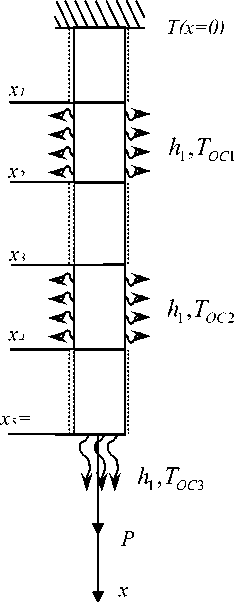
Рисунок. 5. Расчетная схема задачи

Требуется определить величину удлинения одежды от воздействия осевой растя-ГЛЛПЛтіПСЧЛ         !     Р Т = Т (Х = 0) = Тд гивающей   силы   P ,               и температуры      окружающей      сре-

I T  т т

. Здесь надо учитывать, что

некоторые участки одежды теплоизолированы по боковой поверхности. Для этого рассматриваемый стержень длиной L будем

средой, дискретизируем квадратичными

1 ^ _ х₂ - х₁ _ х₄ —х₃

■^4      ^5

элементами с длиной .

Теперь будем исследовать следующие положения, где длина рассматриваемой

L = одежды      равна         , площадь поперечного сечения стержня          ,

-

дискретизировать квадратичными конечны-

ми элементами с тремя узлами.

Теплоизолированную по боковой по-

модуль упругости материала одежды

2 "10          )

, коэффициент тепло-

верхности

0 <  х <  Хр х₂< х < х₃, х₄<  х < L

участки одежды

К — 72 (_хВтн / СЛІ С ^) проводности -                   , коэффи-

дискретизируем на равные элементы. Пусть

элемента

будет

длина         каждого

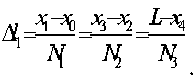
А происходит теплообмен с

циент теплового расширения материала одежда -                 , х^іб^лі) х2 = 32 (елі) х3 = 48(см)

и,                                    ,

,

х . = 64 (елі )

, x ₅ = L .

участки, где окружающей

I-вариант К ^— ^2 ^—^з — 10 (Sm / см С), Т_ос11 — Т_0С2 — Т_осз — 20 ( С)

Число конечных элементов 800. Число узловых точек 1601. Длина конечных элементов одинакова: Л/ = 80 (см) /800 = 0,1 (см) одинакова:

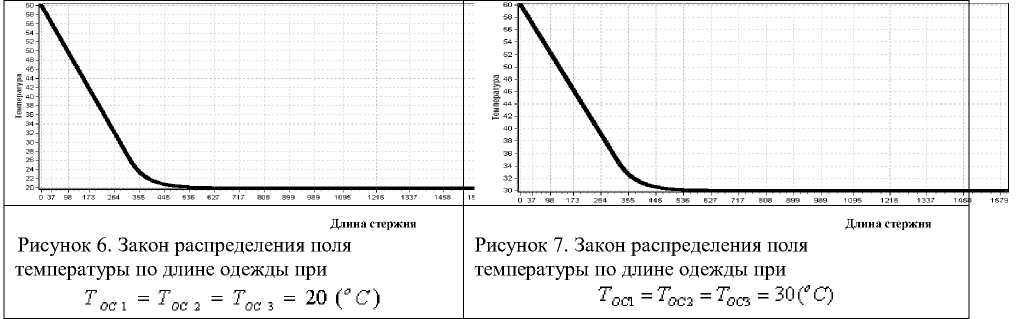
В таком положении значения температуры в 1601 узловых точках одежды приведены в табл. 1. А поле распределения темпе- сунке 6. В этом рисунке по оси абцисс расположены номера узловых точек одежды, а по оси ординат - значения температуры.

Из рис. 6 и табл. 1 видно, что в этом варианте поле распределения температуры по длине одежды выражается через равномерную непрерывную кривую.

ратуры по длине одежды приведено на ри-

Таблица 1 - Закон распределения поля температур в фиксированных точках стержня при

^oci - ^ос2 - ^осз - 20 ( С)

T1=	T350=	T700=	T1050=	T1400=
60,0000000	23,9191529	20,0457544	20,0019617	20,0000559
T50=	T400=	T750=	T1100=	T1450=
54,8458907	21,7101294	20,0386337	20,0008571	20,0000478
T100=	T450=	T800=	T1150=	T1500=
49,5865956	20,7468463	20,0315131	20,0003769	20,0000397
T150=	T500=	T850=	T1200=	T1550=
44,3273004	20,3276018	20,0243924	20,0001714	20,0000316
T200=	T550=	T900=	T1250=	T1600=
39,0680053	20,1469982	20,0172718	20,0000906	20,0000235
T250=	T600=	T950=	T1300=	T1601=
33,8087101	20,0734752	20,0101511	20,0000721	20,0000233
T300=	T650=	T1000=	T1350=
28,5494150	20,0528751	20,0044952	20,0000640

Здесь удлинение одежды от поля распреления температуры по длине одежды

/Vг - ct jT(x )^ - 0,0248791929(см) соответственно [2] будет равно       °                         .

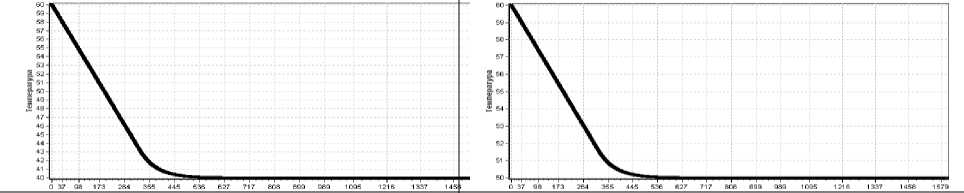
Длина стержня

Рисунок 8. Закон распределения поля температуры по длине одежды при

Tocv-Toc^Tom=A

Длина стержня

Рисунок 9. Закон распределения поля температуры по длине одежды при

^оа ⁼ Тоса ⁼ Тхз = 50( О

п ^i — ^2 — ^з — ІО^ли/сл; С),7         — 2ОСЗ — 30( С)

ІІ-вариант. Пусть

Для этого варианта полученные числовые результаты показаны в таблице 2. Поле распределения температуры по длине одежды выражается через равномерную непрерывную кривую. Оно приведено на рисунках 6,7. А также в этом варианте удлинение стержня от поля температуры

будет

.

равно Д/у —0,0336593947(см)

.

Сравнивая результаты, полученные в І-ІІ

вариантах видим, окружающей среды

когда температура

увеличивается

на

50%                            _,

то

удлинение одежды увеличивается на 132,84%.

Таблица 2 - Закон распределения поля температур в фиксированных точках стержня при

T1= 60,0000000	T350= 32,9393647	T700= 30,0343158	T1050= 30,0014712	T1400=
T50= 56,1344181	T400= 31,2825971	T750= 30,0289753	T1100= 30,0006428	30,0000419
T100= 52,1899467	T450= 30,5601347	T800= 30,0236348	T1150= 30,0002827	T1450=
T150= 48,2454753	T500= 30,2457014	T850= 30,0182943	T1200= 30,0001285	30,0000358
T200= 44,3010040	T550= 30,1102487	T900= 30,0129538	T1250= 30,0000679	T1500=
T250= 40,3565326	T600= 30,0551064	T950= 30,0076133	T1300= 30,0000541	30,0000298
T300= 36,4120612	T650= 30,0396563	T1000= 30,0033714	T1350= 30,0000480	T1550= 30,0000237 T1600= 30,0000176 T1601= 30,0000175

IІI-вариант. Пусть ^і - ^2 - ^з - 10(5wj !см CYTq^ - T_om - Т_от - 40 ( С)

Тогда, сравнивая с I вариантом, видим,

что при увеличении температуры окружаю-

щей        среды        в        два

(pmT_QC = гОСОдоГдс =40(‘^,С'))

раза                               , удли-

Численные результаты, полученные в этом варианте, приведены в табл. 3. Здесь поле распределения температуры по длине стержня показано в виде рис. 8.

нение одежды увеличивается на 177,99%.

IV-вариант. ПустьҚ. —һ^—һз —10(Sm/см СУуТ^^ —Т^ —^осз — 50( С)

Здесь по сравнению с I-вариантом

температура окружающей среды ется (сот Т_ос - 20 (°C) до Т_ос - 50 (°C))

зультате    удлинение    одежды

Д1= 0,0512197982 (см )

дет                                   .

меня

В ребу-

По

сравнению с I-вариантом удлинение одежды увеличивается на 198,51%. Закон распределения поля температуры по длине одежды приводится в виде табл. 4 и рис. 9.

Таблица 3 - Закон распределения поля температур в фиксированных точках одежды при

Тос,=Тоа=Тоа=Д^С)

T1= 60,0000000	T350= 41,9595765	T700= 40,0228772	T1050= 40,0009808	T1400=
T50= 57,4229454	T400= 40,8550647	T750= 40,0193169	T1100= 40,0004286	40,0000279
T100= 54,7932978	T450= 40,3734231	T800= 40,0157565	T1150= 40,0001885	T1460=
T150= 52,1636502	T500= 40,1638009	T850= 40,0121962	T1200= 40,0000857	40,0000231
T200= 49,5340026	T550= 40,0734991	T900= 40,0086359	T1250= 40,0000453	T1500=
T250= 46,9043551	T600= 40,0367376	T950= 40,0050756	T1300= 40,0000361	40,0000198
T300= 44,2747075	T650= 40,0264375	T1000= 40,0022476	T1350= 40,0000320	T1550= 40,0000158 T1600= 40,0000117 T1601= 40,0000117

Таблица 4 - Закон распределения поля температур в фиксированных точках одежды при

Tqci ⁼^oa = T_0C3 = 50 ( C)

T1=	T350= 50,9797882	T700= 50,0114386	T1050= 50,0004904	T1400=
60,0000000	T400= 50,4275324	T750= 50,0096584	T1100= 50,0002143	50,0000140
T50=	T450= 50,1867116	T800= 50,0078783	T1150= 50,0000942	T1450=
58,7114727	T500= 50,0819005	T850= 50,0060981	T1200= 50,0000428	50,0000119
T100=	T550= 50,0367496	T900= 50,0043179	T1250= 50,0000226	T1500=
57,3966489	T600= 50,0183688	T950= 50,0025378	T1300= 50,0000180	50,0000099
T150= 56,0818251 T200= 54,7670013 T250= 53,4521775 T300= 52,1373537	T650= 50,0132188	T1000= 50,0011238	T1350= 50,0000160	T1550= 50,0000079 T1600= 50,0000059 T1601= 50,0000058

Заключение, выводы

Таким образом, на основе анализа существующих математических моделей электризации защитной одежды определены критерии для разработки новой математической модели системы «Человек - Одежда – Среда», позволяющие описать процессы электризации в одежде в жарких климатических условиях.

На основе полученных дифференциальных уравнений были найдены значения температуры для специальной одежды ограниченной длины в узловых точках. При этом, количество узловых точек равно 1601, количество связанных элементов равно 800. В области распределения температуры по длине одежды в четырех различных вариантах было обнаружено, что в I варианте

^AlT^0,0249⁽см), во ii варианте A/_r = 0,033⁷⁽см), в in варианте ^AlT = ^0,0413( см), в IV варианте М_т =0,0512 (си) л _г

^{T , см} , в V варианте ^Al_T =^0,0600(см), в ух варианте длина одежды в этой области увеличилась на 10% по сравнению с длиной одежды во II – варианте. Разработанная математическая модель описывает процессы электризации в поперечных сечениях пакета одежды и на поверхностном слое кожи человека и позволяет рассчитать параметры антистатической одежды для защиты от повышенных температур.

Предложенная математическая модель позволяет определить условия проведения экспериментов, оптимизировать основные параметры, а также оценить эффективность подбора материалов и конструктивных параметров одежды на этапе проектирования.

На основе разработанной математической модели была изготовлена экспериментально-опытная партия специальной антистатической одежды на предприятиях ООО " Al-Hakim Plus" и ООО "Okean-Lyuхе"(Бухарская область). Разработанная новая антистатическая спецодежда была положительно оценена потребителями данной спецодежды - сотрудниками ООО "Региональные электрические сети» Бухарской области и специалистами швейных предприятий. Годовой экономический эффект от внедрения в производство новой спецодежды составил 309 060 000 рублей.