Постановка начально-краевой задачи о перестройке трабекулярной костной ткани

В настоящее время существует множество неоднородных материалов, имеющих сложное внутреннее строение. То же самое относится и к объектам естественного биологического происхождения, таким как кость. Свойства таких материалов определяются, в том числе, их строением, структурой [5, 6, 11, 16, 17, 22, 32, 41, 52].

В частности, известно, что трабекулярная (губчатая) костная ткань является неоднородной пористой анизотропной структурой. Механические свойства губчатой костной ткани также анизотропны и в значительной мере определяются её внутренней архитектурой [17, 22, 26, 27, 29]. Многие задачи биомеханики зубочелюстной и опорнодвигательной систем человека требуют описания напряжённо-деформированного состояния губчатой костной ткани с учётом формирования её структуры во времени при изменении внешних нагрузок [5, 11–14, 17, 50, 51, 56].

Например, при постановке задач об определении напряжённо-деформированного состояния в нижней челюсти человека необходимо учитывать не только неоднородность свойств твёрдых и мягких тканей, но и их внутреннюю © Киченко А.А., Тверье В.М., Няшин Ю.И., Осипенко М.А., Лохов В.А., 2012

Няшин Юрий Иванович, д.т.н., профессор, завкафедрой теоретической механики, Пермь Осипенко Михаил Анатольевич, к.ф.-м.н., доцент кафедры теоретической механики, Пермь Лохов Валерий Александрович, к.ф.-м.н., доцент кафедры теоретической механики, Пермь структуру [11–14, 17, 22, 32]. Таким образом, необходимо иметь способ количественного описания формирующейся под воздействием изменяющегося биомеханического давления структуры костной ткани для различных отделов зубочелюстной системы [5, 6, 11–14, 17].

В связи с этим возникает необходимость введения величины, которая учитывала бы структурные особенности губчатой кости и могла бы быть легко встроена в зависимость строение – свойства материала, иначе говоря, в количественное описание микроструктуры кости [16, 52]. Для подобной величины необходимо сформулировать соотношение, способное описывать упругие свойства материала с учётом его строения.

Также данную величину следует включить в эволюционные уравнения, способные описывать адаптационные процессы и связанные с ними изменения строения костной ткани, происходящие при изменении условий нагружения в губчатой кости. Направленный характер перестройки трабекулярной архитектуры говорит о том, что векторная или тензорная характеристика больше подходит для объективизации процесса [52].

В настоящее время считается, что одним из наиболее удачных способов [5, 9, 17, 22, 32, 41, 52, 57, 60–62] описания локальной структуры многих пористых и композиционных материалов и, в частности, локальной структуры губчатой кости (в том числе степени её анизотропии) является симметричный, положительно определенный тензор второго ранга, названный тензором структуры ( fabric tensor ) и обозначенный как Η ^~ [22, 23, 26, 38, 39, 45, 46, 52].

Тензор структуры, построенный для губчатой костной ткани в соответствии с ранее описанной методикой [6, 17, 37, 57, 60–62], позволяет компактно в тензорной форме описать анизотропию костной структуры, причём его главные значения позволяют охарактеризовать распределение материала вдоль главных направлений [5, 17, 38, 52].

В настоящее время не существует единой формы записи соотношений, связывающих напряжённо-деформированное состояние материала (например, губчатой кости) с его строением (трабекулярной микроструктурой), хотя данной проблеме посвящён целый ряд работ [16, 18–27, 30–36, 38, 40–42, 46, 48, 49, 52, 54, 55, 58, 59, 64]. Однако имеется серия общепризнанных соотношений [21–27, 40, 52, 54, 55], включающих в себя тензор структуры и способных отразить внутреннее строение губчатой кости. То же касается и эволюционных уравнений, описывающих изменения в строении губчатой кости под воздействием различных нагрузок, например, под воздействием изменяющегося биомеханического давления [21, 22, 28, 31, 32, 41, 43, 49]. В данной работе соотношения [21] будут подробно проанализированы и уточнены. На их основе будет представлена постановка начально-краевой задачи о перестройке трабекулярной костной ткани, решение которой позволяет проследить изменение напряженно-деформированного состояния при формировании трабекулярной структуры согласно закону Ю. Вольфа [63].

Вывод определяющего соотношения

Известно, что плотность, пористость и ориентация трабекул в губчатой кости, так же как и упругие свойства костной ткани, изменяются в довольно широком диапазоне в зависимости от исследуемой области. Таким образом, определяющие соотношения должны описывать напряжённо-деформированное состояние губчатой костной ткани, если известны величины, определяющие ориентацию трабекул в рассматриваемой области, и некоторые упругие характеристики материала, которые зависят от плотности костного матрикса, но не зависят от ориентации трабекул (такие характеристики могут быть определены эмпирически после исследования ряда образцов костной ткани).

Экспериментально показано [21, 22, 41], что наблюдаемые в трабекулярной костной ткани деформации не превосходят 0,5%, т.е. они являются малыми [3, 7, 8]. В случае малых деформаций можно воспользоваться основными положениями линейной теории упругости.

Установлено [27], что механические свойства губчатой костной ткани в значительной мере определяются её внутренней архитектурой (геометрией). Костная ткань является анизотропной и неоднородной как в своём строении, так и в своих механических свойствах. При этом в первом приближении считается, что костный матрикс в губчатой кости (пористом упругом теле) изотропен [22, 27] и вся неоднородность губчатой кости связана с геометрией анизотропной микроструктуры трабекулярной костной ткани. В этом случае анизотропия губчатой кости описывается посредством тензора структуры, а тензор упругости и тензор структуры связаны некоторой функциональной зависимостью.

Механические свойства трабекулярной кости (такие как удельная упругость [22, 27]) также зависят от её пористости или связанной с пористостью величины – доли твёрдого объёма кости ν, которая определяется как отношение объёма, занимаемого трабекулярной костной тканью в исследуемом образце V bone , к объёму всего образца губчатой кости V total [41], т.е.

ν=

V bone

V . , total

Таким образом, тензор упругости должен связывать компоненты тензора напряжений с компонентами тензора деформации в упругом материале с наведённой анизотропией [22]. При этом упругие свойства материала зависят от пористости губчатой кости (т.е. от ν) и от ориентации трабекул (т.е. от тензора Η ^~ ). Математически [10, 27] это выразится в том, что в самом общем виде тензор напряжений σ ^~ является

изотропной функцией тензора малых деформаций ^~ ε , тензора структуры Η ^~ твёрдого объёма кости ν:

и

доли

σ ^~ = σ ^~(^~ ε , Η , ν ) .

Здесь мы имеем дело с тензорной функцией ^~ σ двух тензорных аргументов ^~ ε также скалярного инварианта ν. При этом должно выполняться условие

Q⋅σ~⋅QΤ=σ~(Q⋅~ε⋅QΤ,Q⋅Η⋅QΤ,ν)

~ и Η и

для всех ортогональных преобразований Q [16, 44]. Дальнейшие преобразования связаны с поиском наиболее простой формы определяющего соотношения (2), не противоречащей теории определяющих соотношений и не уменьшающей их общности [10, 16].

Исходя из своего определения [17], тензор структуры является симметричным, положительно определённым тензором второго ранга. Тензор малых деформаций также является симметричным тензором второго ранга. Будем считать, что тензор напряжений также симметричный (т.е. предположим, что мы действуем в рамках теории симметричной упругости). В этом случае в соответствии с выводами, представленными в работах [2, 7, 10, 16] для описанного класса изотропных функций, можно конкретизировать соотношение (2) в виде следующего полиномиального разложения:

а = 10 Ei+11s+12s2 +13iH +14H2 +15(s-h+h •£)+

+16(s-iH2+h2-s)+17(s2-iH+Hi-s 2)+18(s2-iH2 +ih 2-s 2),

б

а

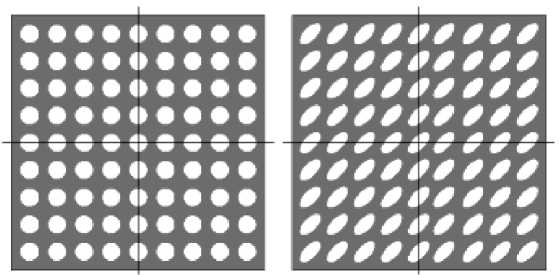
Рис. 1. Тестовые изотропная (а) и структурированная (б) пористые микроструктуры где E - единичный тензор; Iа - изотропные скалярные функции. Соотношение (4) будет получено в том случае [16], если функции Iа (по а не суммировать!) будут представлены в виде полиномов от элементов целого рационального базиса для тензоров-аргументов s и Н [10]. То есть полиномиальные функции Iа должны зависеть как от инвариантов тензоров-аргументов, так и от скалярной величины v:

(8,   8     8,        ~        8          ~         ~ v, trs, trs2, trs3, trН, trН2, trН3, tr(s -Н), tr(~ -Н2), tr(s2 -Н), tr(s2 -Н2)). (5)

В дальнейшем костная ткань будет рассматриваться как линейно-упругий материал с наведённой анизотропией [22]. Известно, что для случая линейной упругости связь между тензором напряжений и тензором деформации выражается законом Гука [3], при этом тензор упругости полностью характеризует линейноупругое механическое поведение материала. В этом случае соотношение (4) может быть записано как

^8                   .^8                                  ,^8               ^8           ^8,^8

О = Iо E + /18 +I3Н +I4Н +I5( s-H + H-s ) +I б( 8-Н + Н -8 ),(6)

где полиномиальные функции I _а можно представить в общем виде как

(88^8    88

v, trs, trН, trН2, trН3, tr(s -Н), tr(s -Н2)).

Таким образом, соотношение (6) в общем виде принимает следующий вид:

5 = C(Н, v) --8 ,(8)

а упругие свойства материала (т.е. тензор упругости C ) зависят от его удельной плотности, ориентации трабекул в пространстве и абсолютной степени анизотропии материала.

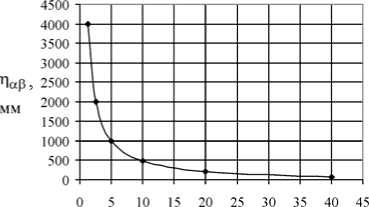
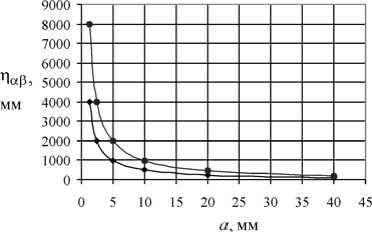
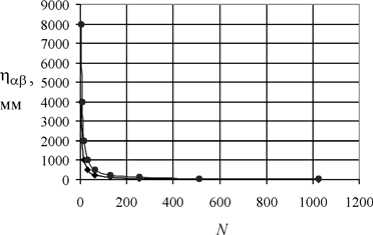
При описании структуры костной ткани посредством тензора структуры прежде всего интерес представляет относительная степень анизотропии губчатой кости [17] (за придание жёсткости материалу отвечает величина v [22, 27]). Ранее [17] авторами было показано, что компоненты тензора структуры главным образом отражают преимущественные направления распределения пор в трабекулярной костной ткани, их ориентацию в пространстве. Видно, что для тестовых микроструктур (см. рис. 1) компоненты тензора структуры в определённом диапазоне слабо зависят от размера пор или от их количества (рис. 2, 3 и [17]). Также в ряде работ [47, 55] было замечено, что упругие свойства пористого материала не зависят от размера пор. Итак, тензор структуры в дальнейшем можно нормировать таким образом, что tr Н = 1.

— Паа

R, мм

а

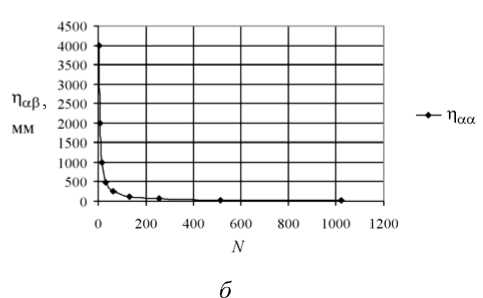
Рис. 2. Зависимость компоненты тензора структуры η αα для изотропного образца: а – от размера пор при их постоянном количестве; б – от числа пор при их постоянном размере

а

б

Рис. 3. Зависимость компонент тензора структуры η_αα и η ββ для анизотропного образца: а – от размера пор при их постоянном числе; б – от числа пор при их постоянном размере

В этом случае от непосредственно тензора структуры Н удобно [21, 22] перейти к девиатору тензора структуры K , определяемому как

K = Н- E . .

Тензор K ^~ по-прежнему отражает распределение пор в губчатой кости, при этом будет выполняться условие tr K = 0.

В этом случае с учётом введённых обозначений соотношение (6) может быть записано как

О = р ₀ E + Р 1 £ + р ₂ K + р ₃ K ² +Р 4 ( £ ■ K + K ■£ ) + Р 5 ( £ ■ K ² + K ² ■£ ),          (10)

где полиномиальные функции βα могут быть представлены в общем виде как v,tr~, trK2,trK3,tr(~^K), tr(~ ■K2)) .                   (11)

Раскроем полученное соотношение. Для этого подставим (11) в (10), при этом следует учитывать, что тензор ~ должен линейно входить в каждое слагаемое соотношения (10). То есть получаем, что

Р0 = a1 tr £ + a2 tr(£ ■ K) + a3 tr (£ ■ K2), в = b0,

P ₂ = c 1 tr £ + c ₂ tr( £ ■ K ) + c ₃ tr ( £ ■ K ²),                                , .

p ₃ = d 1 tr £ + d ₂ tr( £ ■ K ) + d ₃tr( £^ K 2 ),

P4 = P 0, в5 = q 0’ где aα, bα, cα, dα, pα и qα – полиномиальные функции вида

I „ = I „ ( v ,tr K ² ,tr K ³ ) .                              (13)

В итоге получаем:

a 1 tr £ + a ₂ tr( ~ ■ K ) + a ₃ tr( ~ ■ K ²) ) E + b ₀ ~ + ( c 1 tr £ + c ₂ tr( ~ ■ K ) + c ₃ tr( ~ ■ K ²) ) K +

+ ( d 1 tr £ + d ₂tr( £ ■ K ) + d ₃tr( £ ■ K ²) ) K ² + p ₀ ( s■ K + K ■£ ) + q ₀ ( e■ K ² + K ² ■£ ) .

Соотношение (14) аналогично определяющему соотношению из работы [27] (см. также [21, 22, 52]). Отличие от работы [27] заключается в том, что в качестве параметра структуры авторами используется девиатор тензора структуры.

Воспользуемся упрощающим предположением из работ [10, 27], а именно после подстановки в соотношение (13) полиномиальных функций (14) отбросим все слагаемые, чья общая степень превосходит n = 2. Линеаризация ( n = 1) определяющего соотношения невозможна, поскольку в этом случае независимые компоненты тензора упругости станут функционально связанными [27]. В результате подобного упрощения было получено следующее соотношение:

(j = ( ( a ₁₀ + a ₁₁v)tr £ + a ₂₀ tr(£ ■ KL ) ) E + ( b ₀₀ + b ₀₁v)£ + ( c ₁₀tr £ ) KL + p ₀₀ ( £ ■ KL + KL ■£ ) , (15) где a 10 , a 11 , a 20 , b 00 , b 01 , c 10 , p 00 – константы.

Видно, что соотношение (15) с точностью до констант совпадает с соотношением, полученным в работе [21]. Осуществим переобозначения, приводящие соотношение (15) к принятому в литературе [22] виду. Для этого введём величину е – изменение доли твёрдого объёма кости относительно отсчётной величины ν 0 , т.е.

e = ^v-v o , (16)

и заменим ею текущую долю твёрдого объёма кости ν [21]. Также заменим константы a 10 , a 11 , a 20 , b 00 , b 01 , c 10 , p 00 соответствующими работе [21] постоянными величинами (при этом необходимо полагать, что a 20 = c 10 [22]). В итоге получим:

a = ( g i + g 2 e )(tr 8 ) E + ( g 3 + g 4 e ) 8 + g 5 ( 8■ K + K -8 ) + g ₆ ( tr( K -8 ) E + (tr 8 ) K ) , (17)

что эквивалентно соотношению (14) из работы [21]. Здесь g 1 – g 6 – константы [21], имеющие размерность [ГПа], поскольку входящий в соотношение (17) тензор структуры был нормирован. Эти константы были определены в работе [55] после серии экспериментов на различных образцах губчатых костей человека и крупного рогатого скота. Тензор упругости, соответствующий соотношению (17), принимает следующий вид:

C ijkl = ^{( g}i ^{+ g} 2 e ) ⁵ y ⁵ kl ^{+ ( g} 3 ^{+ g} 4 ^{e ) 5} ik ⁵ jl ^{+ g} 5 ( 8 ik K lj ^{+ K}ik ^lj ) ^{+ g} 6^ ^ ij^Kkl ^{+ K}ij 8 kl )• ⁽¹⁸⁾

Эволюционные уравнения закона Вольфа для губчатой костной ткани

Костная ткань живого человека является динамической сложной структурой, в которой происходят постоянный обмен веществ, анаболические и катаболические процессы, разрушение старых и создание новых костных трабекул. Заметим, что термин «анаболический» означает «относится к или способствует анаболизму» (процессу ассимиляции питательных веществ и превращению их в составные части клеток, сопровождаемому при этом энергетическими затратами). Термин «катаболический» означает «относится к катаболизму» (процессу расщепления в организме молекул на более простые, часто сопровождаемому высвобождением энергии).

Механические свойства костей подчиняются тем же принципам, что и несущие конструкции, сделанные людьми. Однако способность позвоночных приспосабливать строение своей костной ткани к приложенной нагрузке приводит к такой структуре, которая является очень сложной и, будучи здоровой, исключительно эффективной [17, 41].

Среди законов, описывающих поведение костной ткани под влиянием каких-либо факторов, например нагрузок, закон Вольфа ( Wolff’s law ) является наиболее известным [63], хотя его точная математическая запись до настоящего времени четко и однозначно не разработана. Данный вопрос до сих пор является краеугольным камнем современных исследований [5, 17]. Закон Вольфа отмечает изменение кости (или мягких тканей) вследствие функциональных требований. Каждое изменение в форме или функции сопровождается определенными изменениями во внутренней архитектуре и во внешней форме. Закон Вольфа применительно к живой костной ткани звучит следующим образом: кость приспосабливает свою внешнюю форму и внутреннюю структуру к тем механическим силам, которые она должна выдержать [5, 17, 41, 63].

При математическом описании адаптационных процессов, происходящих в кости с учётом её внутренней структуры (т.е. при построении кинетических уравнений, включающих в себя слагаемые, отображающие внутреннее строение кости), необходимо дать точную математическую форму записи для закона Вольфа. Для этого воспользуемся подходом, описанным в работах [21, 22, 28]. Закон Вольфа для костной ткани говорит о том, что трабекулярная архитектура губчатой кости 42 ISSN 1812-5123. Российский журнал биомеханики. 2012. Т. 16, № 4 (58): 36–52

в локальной области структурно приспосабливается к местному напряженному состоянию костной ткани. При этом структурная адаптация в живой губчатой кости носит направленный характер и трабекулы располагаются закономерно, сообразно тому, какие внешние нагрузки испытывает данная кость [21, 28]. В частности, установлено, что ориентация трабекул в рассматриваемой области губчатой кости совпадает с главными направлениями тензора напряжений в этой же области [22, 28].

Известно, что при изменении внешней нагрузки, оказывающей воздействие на кость, в соответствии с законом Вольфа происходит перестройка костной ткани. Отсутствие перестройки в кости (равновесное состояние, или гомеостаз) предполагает наличие определённого набора условий, при которых нет никаких изменений в геометрии трабекулярной микроструктуры, резорбции или роста кости. Гомеостатическое состояние обладает определённой специфической структурой трабекулярной костной ткани, описываемой как (ν ⁰ , K ^~0 ) (или (ν ⁰ , Η ^~0 )), и соответствующим данной структуре специфическим напряженно-деформированным состоянием кости (σ ^~0 , ^~ ε ⁰ ). Отметим, что напряжение σ ^~0 и деформация ^~ ε ⁰ при гомеостазе фактически находятся в диапазоне изменения напряжений и деформации, в пределах которого не происходит никакой перестройки кости. Величины σ ^~0 и ^~ ε ⁰ являются здесь усреднёнными значениями напряжений и деформации среды за продолжительный промежуток времени, хотя можно использовать и другие способы определения σ и ε .

Поскольку закон Вольфа отражает тот факт, что главные направления тензора напряжений в состоянии гомеостаза (при отсутствии перестройки) совпадают с ориентацией трабекул в губчатой костной ткани, то в равновесном состоянии главные оси тензора напряжений σ ^~0 должны совпадать с главными осями девиатора тензора структуры K ^~0 (или тензора структуры Η ^~0 ), см. [28]. Иначе говоря, тензоры σ ^~0 и K ^~0 должны быть соосными. Совпадение главных осей тензоров σ ^~0 и K ^~0 имеет место в случае, когда скалярное произведение тензора напряжений σ ^~0 и девиатора тензора структуры K ^~0 коммутативно [4, 15, 28], т.е. если выполняется условие, что

σ ^~0 ⋅ K ^~0 = K ^~0 ⋅ σ ^~0 ,                                (19)

то главные оси означенных тензоров совпадают [28].

В большинстве практических задач биомеханики опорно-двигательной системы необходимо описывать не гомеостатическое равновесное состояние, а перестройку костной структуры, происходящую с течением времени, её непрерывную направленную адаптацию к постоянно изменяющимся нагрузкам, например, биомеханическому давлению. При этом изменение нагрузки должно быть достаточным, чтобы вывести губчатую микроструктуру из состояния гомеостаза и запустить в ней адаптационную перестройку.

В частности, перестройка трабекулярной архитектуры губчатой кости может происходить при однократном достаточном изменении нагрузки. Данная ситуация может возникнуть, например, при вживлении в губчатую кость имплантата. Пусть начальная равновесная губчатая микроструктура описывалась при помощи тензора K ^~0 и соответствующего ему начального напряжённо-деформированного состояния ( σ ^~0 , ^~ ε ⁰ ). Далее произошло однократное изменение условий нагружения, запустившее процессы перестройки в губчатой кости и стремящееся привести трабекулярную ~ 1 архитектуру к новому гомеостатическому состоянию с характерной структурой K и соответствующим напряжённо-деформированным состоянием ( σ ^~1 , ^~ ε ¹ ).

а

б

в

г

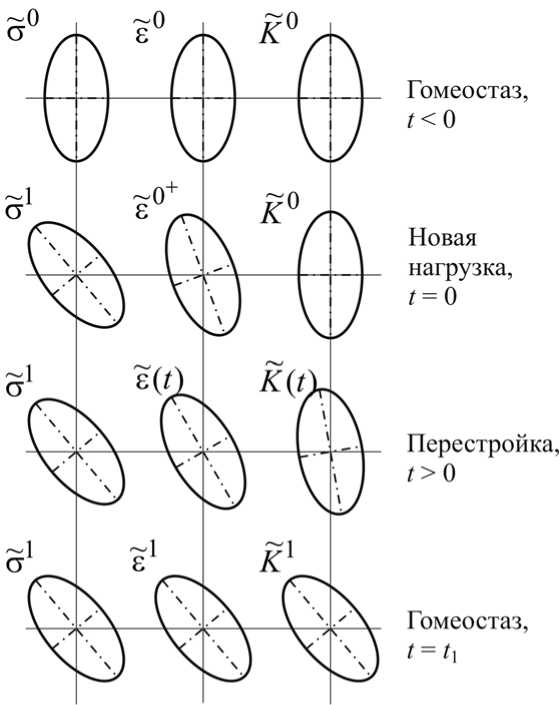
Рис. 4. Схема перестройки трабекулярной костной ткани: а – начальное состояние гомеостаза; б – начало перестройки костной ткани; в – процесс перестройки костной ткани; г – новое состояние равновесия

Описанный адаптационный процесс схематично показан на рис. 4, где тензоры напряжений σ~ , деформации ~ε и структуры K~ представлены в виде эллипсоидов. Рис. 4, а отражает положение, существовавшее при t < 0 и соответствующее начальному состоянию гомеостаза. Видно, что три эллипсоида, представляющих начальные напряжения ~~0, деформацию ~ 0 и структуру К °, соосны, т.е. главные направления тензоров σ~0 , ~ε0 и K0 совпадают (см. формулу (19)).

Рис. 4, б отражает ситуацию начала перестройки костной ткани в момент времени t = 0, когда произошло изменение условий нагружения, соответственно, имеет место новое напряжённое состояние костной ткани σ ^~1 . Напряжённому состоянию σ ^~1

соответствует новое деформированное состояние ^~ ε

0 ⁺

, при этом эллипсоиды σ

~ и ε

0 ⁺

пока что не соосны. В то же время эллипсоид структуры сохранил своё первоначальное ~ направление K , поскольку адаптационные процессы не могут протекать мгновенно.

Рис. 4, в отражает процесс перестройки костной ткани при t > 0. Видно, что эллипсоиды σ~1 , ~ε(t) и K~(t) не соосны, при этом главные направления тензоров ~ε(t) и

~

K(t) изменяются таким образом, чтобы стать соосными главным направлениям нового напряжённого состояния σ~1 . Условием остановки перестройки может служить (19).

Рис. 4, г отражает новое состояние равновесия, которое было достигнуто по прошествии достаточно большого промежутка времени. Новое гомеостатическое состояние может быть описано тензорами напряжений σ ^~1 , деформации ^~ ε ¹ и девиатора

~ 1

тензора структуры K , причём представляющие их эллипсоиды вновь соосны. Таким образом, произошла адаптация трабекулярной костной ткани к новым условиям нагружения.

Из вышесказанного видно, что необходима математическая форма записи закона Вольфа, способная отразить не только отсутствие перестройки костной ткани, но и саму перестройку, т.е. изменение структуры, а следовательно, и изменение тензора K (или Η ), а также изменение доли твёрдого объёма кости е с течением времени. Отметим, что в ряде работ [21, 22, 28, 31, 32, 49] были предложены уравнения, описывающие адаптацию костной ткани к изменяющимся нагрузкам и использующие тензор структуры. Также ряд авторов [22, 32, 43, 64] отмечал, что закон Вольфа может быть частью более общего закона, определяющего скорость изменения тензора структуры как функционал тензора напряжений, деформации, структуры, различных биомеханических факторов, возраста и времени.

При построении эволюционных соотношений необходимо учитывать изменение величин K и е , неизбежно происходящее при перестройке кости. Для построения кинетических уравнений, позволяющих описать перестройку костной ткани в соответствии с законом Вольфа, воспользуемся подходом, предложенным в работе [21]. Для этого введём величины, характеризующие скорости изменения K и е , т.е. ~ dK de                                    ~   .

K = -j- и e = — [21, 22]. При этом скорости изменения K и e зависят от деформации ^~ ε , параметров структуры K и е . •

По аналогии с ранее записанной тензорной функцией (2) скорости изменения K и e могут быть представлены в общем виде как функции двух тензорных аргументов (^~ ε и K ^~) и скалярного инварианта e :

K = f 1 (^~ ε , K , e ),

e = f 2 ( 8 , K , e ).

Здесь K ^~ = 0, т.е. отсутствует изменение ориентации трабекул, при ^~ ε = ^~ ε ⁰ . Изменение доли твёрдого объёма кости отсутствует (т.е. e = 0 ) при e = -v о (костный матричный материал полностью резорбирует), e = 1 - ν ₀ (костный матричный материал заполняет весь объём исследуемого образца) или при ^~ ε = ^~ ε ⁰ [21].

Предположим, что структура и изменение доли твёрдого объёма кости непосредственно не влияют друг на друга [21]. Тогда скорость изменения структуры зависит только от самой структуры и девиатора тензора деформации, а скорость изменения доли твёрдого объёма – только от объёмной плотности и объёмной деформации, тогда соотношения (20), (21) могут быть упрощены следующим образом:

K = f 1 ′ (^~ ε , K ),                                       (22)

e = f‘ (tr~, e ),                                     (23)

где ~ - девиатор тензора ~ , ~ = ~ - 3(tr~) Е . При этом K ~ = 0 при ~ = ~⁰, а e = 0 при e = -ν₀ , e = 1 - ν₀ или при ^~ ε = ^~ ε ⁰ . Условие ^~ ε = ^~ ε ⁰ означает, что у текущего ^~ ε и начального ^~ ε ⁰ тензоров деформации совпадают их главные значения, при этом тензор ^~ ε ⁰ должен быть соосным тензору ^~ ε .

Рассмотрим кинетические уравнения (20), (21). С учётом соотношения (10) уравнение (20) может быть записано как

K = Y0E + Y1~ + Y2K + Y3K2 + Y4(K•~ + ~K) + Y5(K2 •~ + ~K2)(24)

и trK = 0,(25)

~ где K = 0 при £ =£ .

Здесь полиномиальные функции γα могут быть определены аналогично (11) как e,tr~, trK2,trK3,tr(~-K),tr(~-K2)).(26)

Эволюционное соотношение (21) для e можно записать в виде аналогичной полиномиальной функции, т.е. (~     ~     *.~~

• e , tr~, trK2,trK3,tr(~- K), tr(s- K2)),(27)

где e = 0 при e = -V o , e = 1 - v о или при ~ = ~⁰.

Далее подставим (26) в (24), при этом следует учитывать, что тензор ~ должен линейно входить в каждое слагаемое. Например,

• Y 0 = aa i tr ~ + aa 2 tr(~ • K ) + aa 3 tr(~ • K ² ),

• Y i = bb 0 ,

• Y 2 = cc i tr ~ + cc 2 tr(~ • K ) + cc 3 tr (~ • K ² ),

  
  

• Y 3 = dd 1 tr ~ + dd 2 tr(~ • K ) + dd 3 tr(~ • K ² ),

• Y    4 = PP 0 , y 5 = qq 0 , где aa α , bb α , cc α , dd α , pp α и qq α – полиномиальные функции вида

I _a = I _a ( e , tr K ² ,tr K ³ ) .

В результате получим: «

K = ( aa ₁ tr £ + aa ₂ tr( £• K ) + aa ₃ tr( £• K ²) ) E T + bb ₀ £ + + ( cc₁ tr £ + cc 2 tr( £ • K ) + cc 3 tr ( £ • KC ²) ) K + + ( dd ₁ tr £ + dd ₂ tr( £ • K ) + dd ₃ tr ( £ • K ²) ) K ² + + pp ₀ ( K •£ + £ • Kt ) + qq ₀ ( Kt ² •£ + £ • K ² ) .

Применительно к соотношению (30) осуществим упрощение, при котором отбрасываются все слагаемые, чья общая степень превосходит члены второго порядка ( n = 2). Тогда получим:

K = ( ( aa ₁₀ + aa₁₁ e ) tr £ + aa ₂₀ tr( £ • K ) ) E + ( bb₀₀ + bb ₀₁ e ) £ + cc ₁₀ tr £ ) K + pp ₀₀ ( K •£ + £• K ) .

Далее необходимо учесть условие отсутствия перестройки трабекулярной кости, ■ т.е. что K = 0 при ~ =~0. Тогда соотношение (31) преобразуется в

K = ( ( aa₁₀ + aa 11 e )tr( ё-8 ° ) + aa ₂ ° tr(( 8-8 ° ) • K ) ) Ei + ( bb °° + bb ₀₁ e )( 8-8 °) + + CC ₁₀tr( 8-8 ° ) K + pp °° ( K • ( 8-8 ° ) + ( 8-8 ° ) • K ) .

Учтём условие (25) и получим, что

( aa 1° + aa_u e ) tr ( 8-8 ° ) + aa ₂ ° tr(( 8-8 ° ) • K ) =

=^- 3 ( ⁽ bb °° + bb °i e )^{tr( 8 - 8} ° ) + ² pp °° ^{tr ( K} • ^{( 8 - 8} ° )) ) •

Подставим (33) в (32):

K =

( bb °° + bb °1 e ) ( 8 -8 ° ) - - ( bb °° + bb °1 e )tr( 8 -8 ° ) E I+ cc 1° tr( 8 -8 ° ) K +

7                           9

+ pp °° I K • ( 8-8 ° ) + ( 8-8 ° ) • K - ^tr( K • ( 8-8 ° )) E

Видно, что первое слагаемое соотношения (34) включает в себя девиатор тензора 8 - ~ ° . Обозначим его как ~ - ~ ° и приведём (34) к следующему виду:

^ ^Л

К = ( ( bb °° + bb °i e )( 8-8 ° ) ) + cc i° tr( 8-8 ° ) tv +

I ~          А             А    ~            ~          А    ~

+ pp °° I K • ( 8-8 ° ) + ( 8-8 ° ) • K - 3tr( K • ( 8-8 ° )) E I .

Соотношение (35) с точностью до констант совпадает с выражением (15) из работы [21]. Приведём уравнение (35) к принятому в литературе виду. Для этого введём следующие обозначения:

def           def           def             def 3

bb °° = h i , bb °i = h 3 , ^cc _w = h 4 , pp °° =- 2 h 2

В итоге получается соотношение

K = ( h + h ₃ e )( 8-8 ° ) + h ₄tr( 8-8 ° ) K +

+h21(tr ( K ■ (8-8 °))) Ё - 2 (K • (8-8 °) + (8-8 °) • K)

где h 1 - h ₄ - константы [21], имеющие размерность [сут^-1]. Данные константы подбираются эмпирически таким образом, чтобы перестройка костной ткани происходила за время, соответствующее природной действительности (в норме адаптация губчатой кости происходит примерно за 16° дней [21, 22, 32]).

Аналогично из (27) с учётом обозначений для соотношения (16) из работы [21] можно определить, что e = (f1 + f 2e)(tr~ - tre°) + f 3 (tr(K~ • (~ - ~°))), (37) где f -f3 - константы [21]. Данные коэффициенты также имеют размерность [сут-1] и подбираются таким образом, чтобы перестройка костной ткани происходила за время, соответствующее природной действительности (т.е. аналогично постоянным h 1-h4).

С учётом предположений (22) и (32) уравнения (36) и (37) могут быть упрощены следующим образом:

~ ~

K = h 1 (~- ~ 0 ) + h 2 I ( tr( K • (~ - ~ 0 )) ) E - 3 ( к ■ (~ - ~ 0 ) + (~ - ~ 0 ) • K ) 1 ,        (38)

е = ( / 1 + / 2 e )(tr~ - tr~ 0 ) .

Общая постановка начально-КРАЕВОЙ задачи о перестройке ТРАБЕКУЛЯРНОЙ КОСТНОЙ ТКАНИ

Для решения вопросов об исследовании напряжённо-деформированного состояния губчатой костной ткани и протекающих в ней адаптационных процессов будем использовать полученные соотношения (17), (36) и (37).

Рассмотрим ограниченную область V трёхмерного евклидова пространства E ³. Границу области обозначим как S ( S = S _ои S u ), тогда замыканию области соответствует V ( V = V u S ).

В этом случае полная постановка задачи о перестройке трабекулярной костной ткани должна включать в себя:

уравнение равновесия

V - ~ = 0, X е V , t >  0,                             (40)

определяющее соотношение, соответствующее уравнению (17):

~

о = C ( к , е ) •• ~

,

x е V , t >  0 ,

эволюционное уравнение, описывающее изменение ориентации трабекул в рассматриваемой области и соответствующее соотношению (36):

~

d— = /(~, к, е), trк = 0, X е V, t > 0, dt эволюционное уравнение, описывающее изменение плотности губчатой костной ткани в рассматриваемой области и соответствующее соотношению (37):

-- = / > ( £ , K , е ), X е V , t >  0,                          (43)

dt геометрические соотношения Коши:

~ = 1( \ 7 U + mV ), X е V , t >  0,                         (44)

граничные условия:

	Я ■о = P ( t ), X е S о , t >  0,	(45)
	u = 0 ( t ),   X е S u ,   t >  0,	(46)
начальные условия:	— ~ = — ~0, е = е 0, X е V , t = 0,	(47)
	J 5 = J 5 0, X е S о , U = U 0, X е S u , t = 0.	(48)

Видно, что полная постановка задачи в декартовой системе координат в самом общем случае включает в себя 21 скалярное уравнение: три уравнения равновесия, шесть уравнений из определяющих соотношений, шесть кинетических уравнений и 48 ISSN 1812-5123. Российский журнал биомеханики. 2012. Т. 16, № 4 (58): 36–52

шесть геометрических соотношений. В систему уравнений входит 21 неизвестная: шесть компонент тензора напряжения σ _ij , шесть компонент тензора деформации ε _ij , пять компонент девиатора тензора структуры K_ij , изменение доли твёрдого объёма кости e и три компоненты вектора перемещений u_i . Таким образом, полученная система будет статически определимой и можно определить все неизвестные величины.

Далее авторами будет рассмотрено применение соотношений (41)–(43) (или, что то же самое, соотношений (17), (36) и (37)) с учётом начальных условий (47), (48), но без учёта уравнений (40), (44)–(46). Это можно сделать, если предположить, что нагрузки, действующие на рассматриваемую область (а значит и напряжённое состояние рассматриваемой области), не изменяются непрерывно и не вызывают соответствующих перманентных адаптационных процессов в трабекулярной микроструктуре.

Такое возможно, например, при однократном изменении нагрузки и, соответственно, изменении старого напряжённого состояния σ ^~0 на новое σ ^~1 . Тогда система уравнений (41)–(43) в прямоугольной декартовой системе координат в общем случае может быть преобразована в систему, включающую в себя двенадцать скалярных уравнений с двенадцатью скалярными неизвестными.

Заключение

На основе существующих подходов [17, 21, 22, 28] был показан вывод соотношений, способных описать перестройку трабекулярной костной ткани, происходящую вследствие изменяющихся условий нагружения. Осуществлена постановка начально-краевой задачи о перестройке трабекулярной костной ткани, включающая в себя эти соотношения. Далее авторами будет рассмотрена локальная область трабекулярной костной ткани, находящаяся в состоянии гомеостаза в течение достаточно долгого промежутка времени, причём соответствующие напряжённо-деформированное состояние структуры и её архитектура считаются известными. В начальный момент времени произойдёт однократное изменение условий нагружения, приводящее к перестройке трабекулярной микроструктуры. Новое напряжённое состояние в рассматриваемой области при этом также известно и не будет изменяться в течение достаточно долгого промежутка времени.

Благодарности

Работа выполнена при частичной поддержке РФФИ (грант 11–01–00910–а).

ISSN 1812-5123. Российский журнал биомеханики. 2012. Т. 16, № 4 (58): 36–52                      49