Построение базиса для одномерных краевых задач в системах символьных вычислений

Вариационные методы математической физики являются эффективным математическим аппаратом решения краевых задач для дифференциальных уравнений. Наиболее популярные из них — метод Ритца и метод Бубнова-Галёркина.

Метод Бубнова-Галёркина, строго говоря, не является вариационным методом, в том смысле, что для его применения нет необходимости формулировать вариационную задачу. В случае положительно определенного оператора метод Бубнова-Галёркина не дает ничего нового по сравнению с методом Ритца; эти два метода ведут к решению одинаковых систем линейных уравнений и к одинаковым последовательностям приближенных решений. Таким образом, выполнение предположений, необходимых для сходимости метода Ритца означает также выполнение предположений, необходимых для сходимости последовательности Бубнова-Галёркина.

Однако возможности применения метода Бубнова-Галёркина существенно шире, чем у метода Ритца. В методе Бубнова-Галёркина на оператор задачи не налагается никаких существенных ограничений. Не является необходимым, чтобы оператор был положительно определенным, не требуется, чтобы он был симметричным, и он может быть нелинейным. С формальной точки зрения, метод Бубнова-Галёркина, поэтому может применяться даже в случае очень общих операторов.

Хотя методы Ритца и Бубнова-Галёркина ведут в случае линейных положительно определенных операторов к одинаковым результатам, основные идеи этих методов существенно различаются.

Как известно, реализация многих аналитических методов на цифровых компьютерах приводит к вычислительной неустойчивости большинства из них. Это связано с накоплением ошибок округления, возникающих при работе на множестве действительных чисел с ограниченным числом значащих цифр в мантиссе, которое реализуется на цифровых компьютерах.

Так, для получения более точного приближения вариационным методом следует увеличить число используемых координатных функций. При этом возрастает порядок разрешающей системы, но её матрица и свободные члены неизбежно вычисляются с некоторыми, пусть малыми погрешностями. Таким образом, при относительно высоком порядке системы погрешность её решения может оказаться весьма значительной.

Простейший выход из подобной ситуации - увеличение количества значащих цифр, с помощью которых представляются числа на компьютере.

Поэтому решение этой проблемы уже сейчас видится в использовании для некоторых числовых расчетов систем аналитических вычислений, в которых проблемы с ограниченным количеством значащих цифр в мантиссе действительного числа не существует. Например, в системе Maple можно осуществлять расчеты на множестве действительных чисел, имеющих 500 и более значащих цифр в мантиссе своего представления. Это, естественно, скажется на скорости вычислений и потребует использования более мощного компьютера. Однако для многих аналитических алгоритмов, учитывая их простоту, увеличение времени расчета не играет большой роли, так как порядок разрешающей алгебраической системы уравнений, во многих случаях, не превышает нескольких сотен, позволяя получить удовлетворительный для практики результат.

1.    Построение координатных функций в системе Maple

Идея построения базисных функций заключается в специальном подборе линейной комбинации некоторой полной последовательности достаточно гладких, линейно независимых функций таким образом, чтобы удовлетворить однородным граничным условиям. Если речь идет о базисе для метода Ритца, достаточно удовлетворить только главным граничным условиям. В одномерных краевых задачах можно удовлетворить и естественным граничным условиям, - это при использовании метода Ритца значительно повышает точность и улучшает сходимость получаемого приближенного решения. Для метода Бубнова-Галеркина требование удовлетворения всем краевым условиям является обязательным условием. Ясно, что свойства получаемого базиса во многом зависят от свойств функций исходной последовательности. В качестве исходной последовательности можно взять простейшую последовательность x n , n = 0,1,2,... Как известно [1], эта последовательность удовлетворяет необходимым требованиям: при любом n функции линейно независимы; последовательность x ⁿ полна по энергии соответствующего оператора. Способы построения координатных функций опираются на ряд рассуждений, которые трудно сформулировать в виде общего правила. Ниже на конкретных примерах продемонстрируем достаточно универсальный алгоритм, позволяющий построить базис на основе указанной последовательности функций x n , n = 0,1,2,...

Пример 1. Пусть задано дифференциальное уравнение с неизвестной функцией y ( x ), x е [ a , b ]

d-U ( x ) dy) dx dx

+ q ( x ) y = g ( x )

и краевые условия (слева - 1-го рода, справа - 3-го рода)

y ( a ) = 0, 4 y + hy    = 0, h = const.

d^x      x = b

Пусть для определенности

p ( x ) = -----₂; q ( x ) = 1 + e ^{x 2}; g ( x ) = x .

1 + x ²

Пошаговое построение базиса. Пусть M — какое-нибудь определенное натуральное число. Составим сумму £ M = ₁ B i _ ₁ x i ^{_ 1} с произвольными коэффициентами B i . Подставим эту сумму в граничные условия вместо y ( x ) . Получим систему уравнений по граничным условиям.

Например, для M = 6 будем иметь

J a ⁵ B 5 + a ⁴ B 4 + a ³ B 3 + a ² B 2 + aB 1 + B 0 = 0,

I 5 b ⁴ B ₅ + 4 b ³ B ₄ + 3 b ² B ₃ + 2 bB ₂ + B 1 + h ( b ⁵ B ₅ + b ⁴ B ₄ + b ³ B ₃ + b ² B ₂ + bB 1 + B ₀) = 0.

Формируем матрицу коэффициентов при неизвестных B i

	1	a	a 2	a 3	a 4	a 5
A =	h	bh +1	b 2 h + 2 b	b 3 h + 3 b 2	b 4 h + 4 b 3	b 5 h + 5 b 4

Теперь остается построить ядро матрицы A — множество векторов V таких, произведение матрицы A на которые равно нулевому вектору. Поиск ядра матрицы A эквивалентен решению системы линейных однородных уравнений. Ядром матрицы A являются все решения уравнения AV = 0 . В системе Maple есть специальные возможности построения ядра матрицы. Можно, например, воспользоваться командой NullSpace из пакета LinearAlgebra , или командой null из пакета MTM . В нашем случае для матрицы получим следующие векторы

	a abbh - b 2 h + a - 2 b)		a ( a 2 bh - b 3 h + a 2 - 3 b 2)
	ah - bh -1		ah - bh -1
	a 2 h - b 2 h - 2 b		a 3 h - b 3 h - 3 b2
V 1 =	ah - bh -1	, V 2 =	ah - bh -1
	1		0
	0		1
	0		0
	0		0

	a ( a 3 bh - b 4 h + a 3 - 4 b 3)		a ( a 4 bh - b 5 h + a 4 - 5 b 4)
	ah - bh -1 a 4 h - b 4 h - 4 b 3		ah - bh - 1 a 5 h - b 5 h - 5 b 4
V 3 =	ah - bh - 1	, V 4 =	ah - bh - 1
	0		0
	0		0
	1		0
	0		1

В результате получаем базис

V i ( x ) = £ V i , k x^{k - 1}, i = 1,2,3,4, k = 1

или явно

V i ( x ) =

a ( abh - b ² h + a - 2 b ) ( a ² h - b ² h - 2 b ) x

ah - bh -1

ah - bh - 1

+ x ²,

V 2 ( X ) =

a ( a ² bh - b ³ h + a ² - 3 b ²) ah - bh - 1

-

[ a ³ h - b ³ h - 3 b ²) x ah - bh - 1

+ x ³,

V 3 ( x ) =

a ( a ³ bh - b ⁴ h + a ³ - 4 b ³) ( a ⁴ h - b ⁴ h - 4 b ³) x ah - bh - 1            ah - bh - 1

+ x ⁴,

V 4 ( x ) =

a Г a ⁴ bh - b ⁵ h + a ⁴ - 5 b ⁴) Г a ⁵ h - b ⁵ h - 5 b ⁴) x

—------------- - ---------— + x ah - bh - 1           ah - bh - 1

Числовой пример. Пусть a = 0, b = 1, h = 10 . Данная задача не имеет аналитического решения. В системе Maple можно решить эту задачу численно, методом конечных разностей, с помощью встроенной процедуры dsolve , используя опцию numeric . Продемонстрируем, как это сделать. Вводим дифференциальное уравнение и граничные условия:

> ode:=-Diff(p(x)*(Diff(y(x),x)),x)+q(x)*y(x)=g(x): bc:=y(a)=0,D(y)(b)+h*y(b)=0:

Определяем коэффициенты уравнения и правую часть:

> p:=x->1/(1+xA2): q:=x->1+exp(-xA2): g:=x->x: h:=10:

Решаем задачу:

> h:=10: a:=0:b:=1:

> res:=dsolve({ode,bc},y(x),numeric):

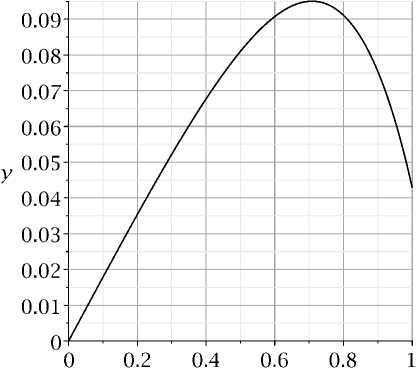
Теперь можно отобразить результат графически (Рис. 1):

> plots[odeplot](res,[x,y(x)],a..b,color=black,legend=‘МКР‘, font=[Times,roman,14],labelfont=[Times,roman,14],gridlines=true);

|----mkp\

Рис. 1. Решение методом сеток.

Можно получить таблицу решений и их производных в выбранных точках:

> dsolve({ode,bc},y(x),numeric,output=

Array([0,.125,.25,.375,.5,.625,.75,.875,1]));

d x y (x)      y (x)

d x

0.	0.	0.178877596144050
0.125	0.0222647111340107	0.176559643581643
0.25	0.0439018319409597	0.168448096626312
0.375	0.0639902293033842	0.150970745894804
0.5	0.0809967202850409	0.117839454837183
0.625	0.0924065948739762	0.0595321194601292
0.75	0.0942741522992380	-0.0374777538410180
0.875	0.0806573036802476	-0.191824555761338
1.	0.0428853692314451	-0.428853692314451

Решим теперь эту задачу методом Бубнова-Галеркина, используя построенный базис. Приведем программу, реализующую построение базиса, удовлетворяющего заданным граничным условиям:

> polynoms_1_3:=proc(M,f) local u,V,B,P,P1,i,k,j,R,psi;

psi:=Array(1..M-2); u:=Vector(1..2,0); V:=Matrix(1..2,1..M,0);

i:=’i’;sum(B[i-1]*xA(i-1),i=1..M);P:=unapply(%,x);

diff(P(x),x);P1:=unapply(%,x);

u[1]:=P(a);u[2]:=P1(b)+h*P(b);

i:=’i’;j:=’j’; for i to 2 do for j to M do

V[i,j]:=coeff(u[i],B[j-1]) end do end do;

R:=LinearAlgebra[NullSpace](V);

i:=’i’;k:=’k’; for i to M-2 do psi[i]:=add(R[i][k]*x^(k-1),k=1..M) end do;

psi:=sort(psi);

i:=’i’; for i to M-2 do psi[i];f[i]:=unapply(%,x) end do end proc:

С помощью этой процедуры построим базис:

> M:=6:polynoms_1_3(M,f):

Образуем аппроксимирующую функцию:

> add(c[n]*f[n](x),n=1..M-2): w := unapply(%, x);

Формируем систему Бубнова-Галеркина:

> eqns := {}: vars := {}:

for j to M-2 do eq[j]:=evalf(int(subs(y(x)=w(x),value(lhs(ode)))*f[j](x),x=a..b)) =evalf(int(rhs(ode)*f[j](x),x=a..b));

eqns:=eqns union {eq[j]};

vars:=vars union {c[j]} end do:

Решаем полученную систему:

> res := solve(eqns, vars): assign(res):

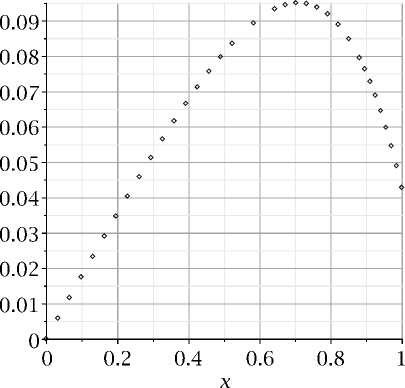
Отобразим результат графически (Рис. 2):

> plot(w(x),x=a..b,style=point,color=blue, legend=cat(‘Бубнов-Галеркин N = ‘,convert(M-2,string)), numpoints=1,font=[Times,roman,14],labelfont=[Times,roman,14], gridlines=true);p||(M-2):=%:

Отобразим для сравнения на одном рисунке два графика (Рис. 3):

> plots[display](p||(M-2),pic1);

Видим, графики практически совпадают! Приближенное решение по Бубнову-Галеркину имеет вид w (x) = 0.177x + 0.0136x2 - 0.106x3 + 0.103x4 - 0.145x5.

Пример 2. В качестве второго примера рассмотрим дифференциальное уравнение четвертого порядка. Пусть задано дифференциальное уравнение с неизвестной функцией y ( x ), x е [ a , b ] .

d2 [     d2y\ d? ^ (x) dx J+ q(x) y = g (x)

и краевые условия dy y (a) = o, — dx

d ² y

= ⁰ d^2 x = a x-x

d ³ y „ = ⁰ d?3 x = b      dx

= 0.

x = b

| ° Бубнов-Галеркин № = V |

Рис. 2. Решение методом Бубнова-Галеркина.

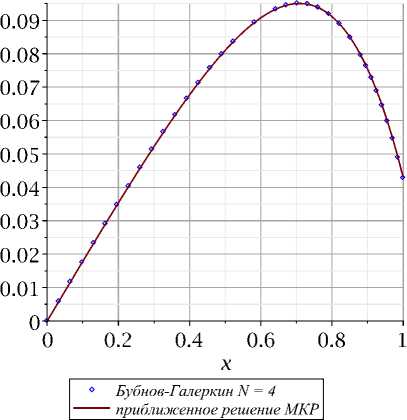
Рис. 3. Сравнение решений.

Выберем коэффициенты уравнения так, чтобы задача наверняка имела бы точное решение. Пусть, например p (x) = 1; q (x) = 4; g (x) = x.

Не останавливаясь на подробностях, приведем окончательные результаты. Будем иметь точное решение

У ( x ) =

-2e ^x sin ( x ) - 2 sin ( x ) e ^{x + 2} - 2e ^x cos ( x - 2) - 2 sin ( x ) e ^{x 2} - 2e ^x sin ( x ) + 2e x cos ( x - 2)

+

8e² + 16cos(2) + 32 + 8e ^{- 2}

+

+2 x e ² + 2 x e² - 2e x cos( x ) + 2e x cos( x ) + 4 x cos(2) + 8 x

8e2 + 16cos(2) + 32 + 8e 2               ’ или, в форме с плавающей точкой y (x) = -0.0234ex sin (x) - 0.0234 sin (x) e-x+2 - 0.0234ex cos (x - 2) - 0.0234 sin (x) ex-2-

-0.0234e ^{- x} sin ( x ) + 0.0234e - ^x cos ( x - 2) + 0.250 x - 0.0234e ^x cos ( x ) + 0.0234e - ^x cos ( x ).

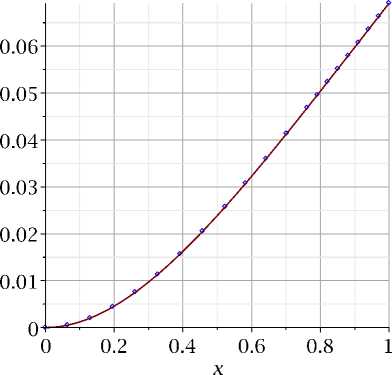
Бубнов-Галеркин N = 3 ----точное решение

Рис. 4. Сравнение решений.

Решение методом Бубнова-Галеркина при трех базисных функциях дает функцию w (x) = 0.00104x4 - 0.0654x3 + 0.127x2 + 0.00682x5 - 0.000346x6.

Сравнение точного и приближенного решения приведено на рисунке 4. Видим, графики практически совпадают!

2.    Метод ортогональных рядов в системе Maple

Теоретические предпосылки. Пусть A — положительно определённый оператор в гильбертовом пространстве H и рассматривается уравнение в некоторой области Ω

Au = f ( P ), P e Q , f e H .                                 (1)

В монографии [2] предлагается следующий алгоритм решения этой задачи. В гильбертовом пространстве H A со скалярным произведением

[ u , v ] A = ( Au , v )

необходимо построить ортонормированную систему функций {ωn}. Тогда решение рассматриваемой задачи можно представить в виде ряда u = E(f, ^n) ^n,                                   (2)

n = 1

который сходится в метрике пространства H .

Если 6 — дельта-функция Дирака и f = б (P0), P0 e Q, то функция (2) будет иметь вид u (P) = £ ton (Pо) ton (P)

n = 1

и называется функцией Грина рассматриваемой задачи.

Описанный метод решения уравнения (1) получил название метода ортонормированных рядов. Как пишет известный чешский математик К. Ректорис в своей монографии [3, стр. 147], в общем случае построить ортонормированный базис в непросто. Эта задача нетривиальна, даже если не требуется ортонормированности базиса. Однако даже если базис найден, его ортогонализация представляет собой, вообще говоря, чрезвычайно трудоёмкий процесс и, как правило, с точки зрения численных расчётов едва ли осуществима. Применение одной из наиболее мощных современных систем символьных вычислений — системы Maple во многих случаях позволяет справиться с этой задачей.

Числовой пример. В качестве примера построим решение уже рассмотренной задачи из примера 1 в форме ортогонального ряда. Для этого нам потребуется ортонормировать полученный в примере 1 базис по энергии оператора задачи. Покажем, как это сделать в Maple. Определим оператор задачи

• >    A:=proc(w) global p,q;

  -diff(p(x)*(diff(w,x)),x)+q(x)*w;

end proc:

Процедура ортогонализации базиса по энергии оператора A и построение функции Грина задачи Ay = g :

• >    GreenFunc:=proc(N,GrFunc,W)

global v,A,p,q,g,f;local F,G,i,ST;

F:=Array(1..N,0);G:=Array(1..N,0);

F:=[seq(f[i](x),i=1..N)]:

G[1]:=evalf(F[1]);

evalf(G[1]/sqrt(int(A(G[1])*G[1],x=0..1)));

v[1]:=unapply(%,x);

for i from 2 to N do

G[i]:=evalf(F[i]- sum(int(A(v[n](x))*F[i],x=0..1)*v[n](x),n=1..i-1));

simplify(evalf(G[i]/ sqrt(int(A(G[i])*G[i],x=0..1))));

v[i]:=unapply(%,x);

end do;

simplify(sum(v[m](x0)*v[m](x),m=1..N));

GrFunc:=unapply(%,x,x0):

int(g(x0)*GrFunc(x,x0),x0=0..1);

W:=unapply(%,x);

end proc:

Решение задачи:

• >    st := time():GreenFunc(N,GrFunc,W):time() - st;

Здесь мы выводим и время выполнения процедуры — 4.687 секунды.

Отметим еще одну особенность. В процессе ортогонализации приходится вычислять интегралы, которые в данном случае не выражаются через элементарные функции — вычисляются через интеграл вероятности (функцию ошибок erf( x ) ). В процедуре при вычислении интегралов использовалась команда evalf для численного (не аналитического!) вычисления с целью уменьшить время выполнения программы.

Отобразим результат графически (Рис. 5):

> plot(W(x),x=0..1,font=[Times,roman,14], labelfont=[Times,roman,14],gridlines=true);

Сравнение рисунков 1-2 и 5 показывает их полную идентичность!

Рис. 5. Метод функции Грина.

Заключение

Изначально задачи математической физики решались аналитическими методами. Непрерывное совершенствование вычислительной техники на некоторое время отвлекло исследователей от развития аналитических методов. Численные методы фактически вытеснили из практики аналитические методы решения технических задач.

Ситуация в корне изменилась с появлением и доступностью персональных компьютеров, а самое главное, с появлением мощных систем аналитических вычислений. В настоящее время все инженерные, конструкторские, экономические задачи можно решать на компьютере, причем в большинстве случаев совершенно нет необходимости заниматься программированием в традиционном смысле. Например, в системе аналитических вычислений Maple пользователь имеет возможность выполнить все расчеты так, как он выполнил бы их на листе бумаги, причем все рутинные и трудоемкие вычисления (а главное, без ошибок и в формульном, аналитическом, виде!) берет на себя система Maple. Системы аналитических вычислений могут в корне изменить отношение к “забытым” аналитическим методам.

Рассмотренные примеры показывают эффективность применения системы аналитических вычислений Maple для построения базиса, удовлетворяющего заданным однородным граничным условиям и решения краевых задач для дифференциальных уравнений с помощью приближенных аналитических методов.

С развитием вычислительной техники и созданием систем аналитических вычислений, таких как Maple или Mathematica, появилась возможность анализа достаточно сложных задач математической физики аналитическими методами. Аналитическими методами стало возможным решать и другие сложные задачи математической физики [4-8].