Построение базового закона движения материальной точки и реализующего его программного управления при наличии фазовых ограничений
Автор: Лутманов С.В.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика
Статья в выпуске: 3 (58), 2022 года.
Бесплатный доступ
Решена задача построения базового кинематического закона управляемого движения материальной точки в однородном поле тяжести с учетом сопротивления среды, пропорционального квадрату величины скорости. В соответствии с этим законом точка обходит заданные запретные зоны и не покидает в процессе полета заданную вертикальную полосу над поверхностью земли. Построено программное управление, реализующее базовый закон движения точки. Составлены дифференциальные уравнения, описывающие динамику возмущений базового движения.
Кинематический закон движения, базовая траектория, фазовые ограничения, программное управление, задача коши, динамика возмущений
Короткий адрес: https://sciup.org/147246609
IDR: 147246609 | УДК: 519.7 | DOI: 10.17072/1993-0550-2022-3-25-37
Текст научной статьи Построение базового закона движения материальной точки и реализующего его программного управления при наличии фазовых ограничений
Эта работа © 2022 Лутманов С. В. лицензируется под CC BY 4.0. Чтобы просмотреть копию этой лицензии, посетите
Данная работа является продолжением цикла статей автора [1–4], посвященных решению задач управления материальной точкой, движущейся в среде с сопротивлением при наличии ограничений на ее фазовые координаты. При решении ряда задач управления движением летательного аппарата, таких как построение пространственных траекторий, определение дальности и высоты полета, попадание в заданную область пространства, перевод из заданной начальной точки фазового пространства в заданную конечную, выбор времени полета, если оно неизвестно, и др. летательный аппарат моделируют как управляемую материальную точку, отождествляя его с центром масс аппарата [5–7]. Особую сложность представляют задачи управления летательным аппаратом при наличии фазовых ограничений на его траекторию: наличие запретных областей, необходимость движения вдоль заданного коридора и др. [8-11], [12, 13].
Решение таких задач основывается на концепции обратных задач динамики, которая включает в себя два этапа: задание кинематического закона движения точки, удовлетворяющего основным требованиям, предъявляемым к полету аппарата и построение программного управления, реализующего этот закон движения. Кинематический закон движения ищется обычно в виде полиномов подходящей степени [14]. Движение материальных тел в среде с сопротивлением рассматривались в работах [15-18].
1. Постановка задачи и общая схема исследования
Полет управляемой точки происходит в однородном поле тяжести при сопротивлении воздуха пропорциональном квадрату скорости точки в течении заданного промежутка времени. Движение точки начинается из начального положения с поверхности земли путем "почти вертикального" подбрасывания ее на определенную высоту, где она приобретает некоторую начальную скорость. Дальнейшее движение точки осуществляется под действием управляющей силы и заканчивается в заданном конечном положении (цели полета).
Полет будем рассматривать в прямоугольной декартовой системе координат Oxyz . Начало координат поместим на поверхность земли в исходное положение точки.
Ось Oz направим вертикально вверх, оси Ox и Oy — горизонтальны. При этом плоскость Oxz проведем через точку-цель.
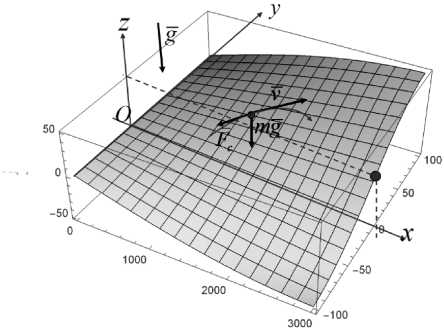
Рис. 1. 3D график рельефа местности
"Почти вертикальное" подбрасывание точки в данной работе не моделируется. Отсчет текущего времени начинается с момента t 0 — выхода точки на высоту подбрасывания и заканчивается в момент времени T — попадания в цель. Величины t^ и T считаются
заданными.
Динамика полета описывается обыкновенным векторным дифференциальным уравнением
mr =— k • Irl • yr + v + mg ^ , r
r = — —.rI.r + 2v + g, t €[10,T] (1)
mm
где t — текущее время, r =
g R 3 — ради-
ус-вектор точки относительно начала коорди-
нат, m —
масса точки, v =
v x
v
e R3
—
вектор
управляющих параметров, компонентами которого являются проекции вектора управляющей силы на соответствующие оси, g — вектор ускорения силы тяжести, к — коэффициент пропорциональности.
В координатной форме векторное уравнение (1) имеет вид:
■■ ■ 2 . -2 . -2 ■ . 1
X —--x х + y + Z X +— vx , mm
•• k • 2 , -2 • , 1
y —--xx + y + z y + — vy, mm
k
Z —--X* + y+ z
m t e[to,T].
. 1
Z + — v z - g , m
Рельеф местности задается функцией p : R 2 ^ R 1, p ( 0,0 ) — 0.
( *
Тогда для точек поверхности земли y
Iz )
справедливо равенство
z — p( x, y), z ( 0,0) — 0.
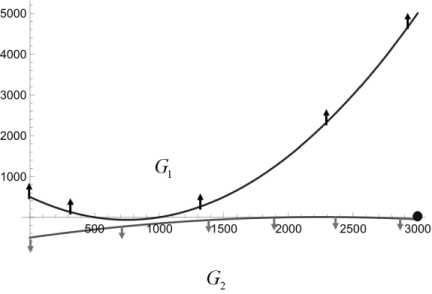
На рис. 1 показана введенная система координат, приложенные к точке силы и положение цели. На плоскости Oxy имеются открытые области:
G j c Oxy , j — 1,2,---, s .
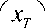
yT
Относительно цели r
потребуем,
чтобы она находилась на поверхности земли, а ее горизонтальная проекция вне областей Gj c Oxy , j — 1,2, • • •, s , т. е.
zT — p ( X t , У т ) ,
xT
< y T )
£ G j , j — 1,2,
, s .
В силу выбора системы координат вы- полняется yT — 0 . Задана величина
0 < x* < xT . Сформулируем требования к закону движения управляемой точки. В процессе полета для горизонтальной проекции управляемой точки запрещено попадание внутрь множеств Gj c Oxy, j — 1,2, • • •, s . Са- ма точка должна находиться в полосе:
S .
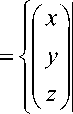
ф ( x , y ) + s < z <
< p(x,y) + 2s, s > 0} над поверхностью земли вплоть до достижения ею координаты x — x*.
В дальнейшем точка начинает снижение и попадает в цель в конечный момент времени T .
Определение 1. Интегрируемую вектор функцию v : [ t 0, T ] ^ R3 будем называть программным управлением материальной точкой на промежутке времени [ t 0, T ] .
Пусть v ( • ) - программное управление. Символом
r ( t ) — r ( t , t 0 , r 0 , r 0 , v ( • ) ) , t e [ t 0 , T ]
обозначим кинематический закон движения материальной точки, порожденный программным управлением v (•) и выходящим из начального положения r с начальной скоростью r . Этот закон r (t), t е[ t0, T] опре деляется как решение задачи Коши для обыкновенного векторного дифференциального уравнения
r —- —• IrI-r + — v (t) + g, mm r (t0 ) — r0*, r(t0 ) — r0*, t € [t0,T].
Задача состоит в построении такого программного управления v0 (•), для которого кинематический закон движения точки r0 (t) — r(t,t0,r0,r0,v0 (•)), t e[t0,T], им порожденный, удовлетворял бы всем вы-шесформулированным требованиям к полету точки.
Решение этой задачи предлагается осуществить по следующей схеме. Подбирается закон движения точки r — rbaz (t), t e[10,T] , удовлетворяющий всем требованиям к полету. Строится программное управление vbaz (•) по формуле
rbaz — - • Irbaz I • rbaz + ~ vbaz (t) + g ^
mm
vba- (t ) — mra (') + k • Iraz I r- - g.
t 4 ‘ 0 , T ].
Определение 2 . Закон движения точки ha z(-) и программное управление vba z(-) будем называть базовым законом движения и базовым программным управлением точки.
x 0
Пусть r o = у о
, zn
начальное положение и
x o r o = у о
I Z n
— начальная скорость точки, кото-
базового программного управления, реализующего этот закон. Задача совмещения возмущенного и базового движения в момент времени T в данной роботе не решается. Она служит предметом дальнейших исследований.
2. Алгоритм построения базового закона движения точки
рые она приобрела после этапа "почти вертикального подбрасывания".
Определение 3 . Закон движения точки r oz ( t ) = r ( t , t о , r o , r o , vbaz ( • ) ) , t e [ t 0 , T ]
будем называть возмущенным движением, а разность
^r ( t ) = roz ( t )-rbaz ( t ) , t £[ to, T ]
– возмущением базового движения.
В общем случае в силу rbz (to)* ro, rbaz (to> ro возмущенный закон движения не совпадает с базовым законом движения и поэтому он не обязан удовлетворять требованиям, предъявляемым к полету точки. Идея предлагаемого подхода состоит в ведении дополнительного управления и (•) , входящего в дифференциальные уравнения движения аддитивно основному управлению у (•) , и которое совмещает возмущенное движение с базовым в некоторый момент времени T < T . После чего дополнительное управление отключается. В силу теоремы существования и единственности решения дифференциального уравнения, дальнейшее движение точки на промежутке времени ^T", T ] будет происходить в соответствии с базовым законом движения. В предположении, что до момента времени T нарушения фазовых ограничений не происходит, реализованное описанным образом программное управление v0 (•) = vbaz (•) + и (•) порождает закон движения точки, удовлетворяющий всем сформулированным требованиям.
Задача совмещения возмущенного и базового движения эквивалентна задаче обнуления возмущения. Динамику возмущения можно приближенно описать уравнениями управляемого движения точки, линеаризованными в окрестности пары "базовое управле-ние-базовое движение".
В данной работе решается задача построения базового закона движения точки и
Дадим формальную постановку задачи по построению базового закона движения точки.
Дано:
дифференциальные уравнения динамики точки (1);
[ t 0, T ] — промежуток времени, в тече-
ние которого происходит полет;
Z = ф(X, у ), (X, у ) G R2 — функция, описывающая рельеф местности;
G^ о Oxy , j = 1,2, • • •, s — открытые об-
ласти, внутрь которых запрещено попадать горизонтальной проекции управляемой точки;
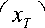
y
IZT J
— радиус-вектор цели, коор-
динаты которого удовлетворяют условиям
zT = ^ ( X t , ут ) , У т = o,
' xT
k yT J
s гUG,;
j = 1
x * — координата управляемой точки на оси Ox , по достижении которой точка начинает снижаться;
8 > o — число, определяющее высоту вертикальной полосы над поверхностью земли, внутри которой должна лежать траектория точки до достижения ею координаты x* по оси Ox .
Задача. Требуется определить
x baz 0
r baz o
y baz o
k Z baz o J
ложения точки;
X baz o
— вектор начального по-
ro =
сти точки;
ybaz о — вектор начальной скоро-
k Z baz o J
vba z(’ ) — программное управление точкой на промежутке времени [ t 0, T ] такие, что для кинематического закона движения точки
[ x baz ( t П
У baz ( t ) = r baz ( t ) =
< z baz ( t )?
= r (t, t0, rbaz0, rbaz0, vbaz (,)) , величина ^rbaz (T) — rT^ мала и xbaz ( t ) Уbaz ( t )
s
j = 1
j ,
t e [ 1 0 , T ] ,
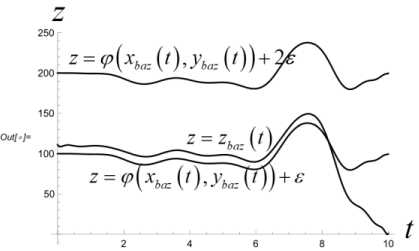
Н x baz ( t ) , yb az ( t ) ) + £ < z baz ( t ) <
< H x baz ( t ) , y baz ( t ) ) + 2£, t € [ t 0 , T * ] где момент времени T* определяется условия xbaz ( T *) = x* •
. По-
Приведем решение поставленной задачи лагаем
= x^-x^ = xL T * = x'
baz 0
T T x baz 0
.
Задаемся натуральным n и разбиваем отрезок времени [ t0, T ] точками:
T 0 = t 0 , T 1 = T 0 + 3,---,T n = T n — 1 + 3 = T ,
T — tn e Л ,
3 =---- 0 ^ т = T + i ‘ 3 , i = 0,1,*", n
n на n промежутков:
[ T 0 , T 1 ) , [ T 1 , T 2 ) , * * *, [ T n — 1 , T n ] .
Не теряя общности, считаем, что
T = т * = т 0 + i -3 для некоторого натурального i * < n .
Строим последовательности:
x ( T 0 ) , x ( T 1 )
У ( T 0 ) , У ( T 1 )
,,
,,
Z ( T 0 ) , z ( T 1 ) ,-,
x (r.*) ,•••, x ( T n — 1 ) , x ( T n ) , У ( T J ,•••, у ( T n — 1 ) , У (T n ) , z ( T r) ’"', z ( T n — 1 ) , z ( T n ) .
В момент времени т0 полагаем:
Х ( т 0 ) = 0 •
Величины у ( т ) , z ( т ) находим как решение задачи математического программирования:
(У(т0)— Ут)2 +(z(T0) — ZT)2 ^min при ограничениях
НХ(T0 ), У (T0 )) + £ < z (T0 )< x (T0 )
У ( T 0 )
s е U°j • j=1
В момент времени т полагаем
x ( т ) = x ( т ) + Х о 3 .
Величины у ( т ) , z ( т ) находим как решение задачи математического программирования:
( У ( T 1 ) - У т ) 2 + ( z ( T 1 ) - z T ) 2 ^ min •
При ограничениях
Н x (Т1), У (Т1)) + £ < z (Т1 )< из
x ( T 1 )
У ( T )
s
^ и ^ .
j = 1
Приведенные построения производятся вплоть до момента времени т * = T * включительно.
В момент времени
Т * +i = T * + $ = T + ( i * + 1 ) 3т = T * + 3 полагаем x ( г ,+1 ) = x (г. ) + x baz0 3 .
Величины у ( т . * +1) , z ( т * +1) находим как решение задачи математического программирования:
( У ( T i -+1 ) — У т ) 2 + ( z ( т г+1 ) — z T ) 2 ^ min .
При ограничениях
^ ( Х ( Т -+1 ) , У ( т -+1 ) ) + £ •
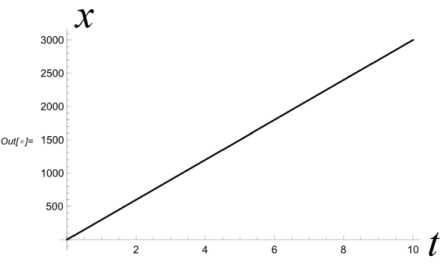
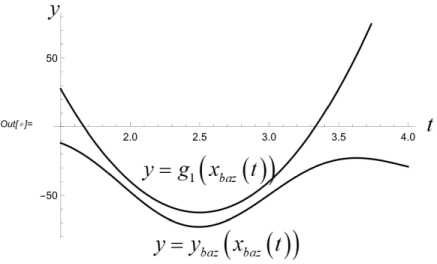
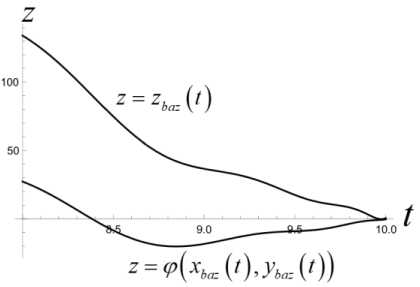
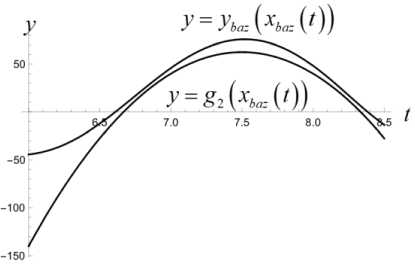
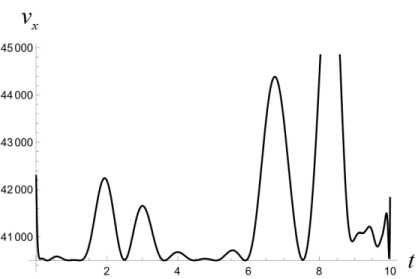
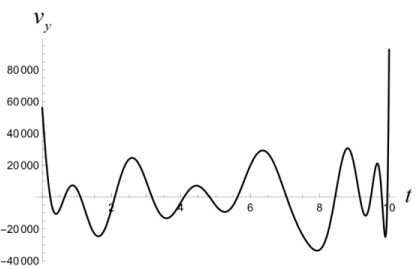
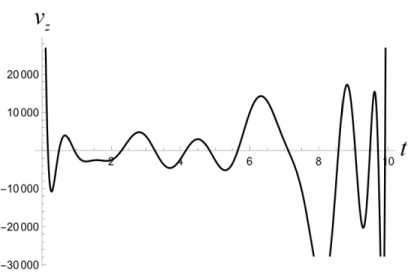
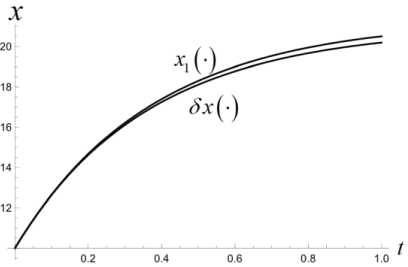
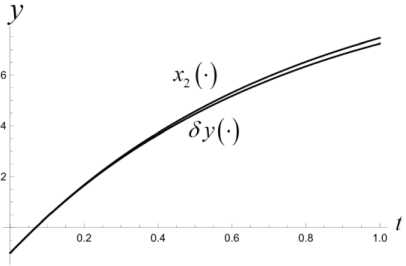
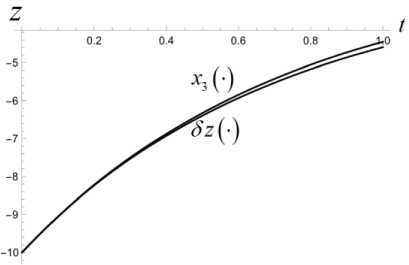
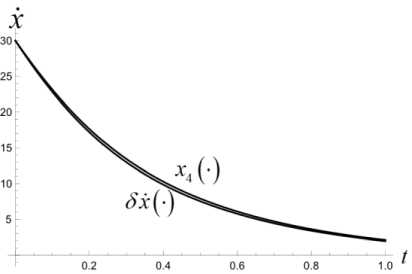
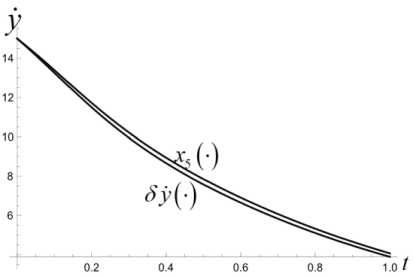
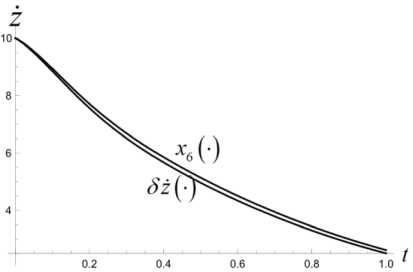
T T'+1 T — т* ' i Z z s < И x (т*+1), У (Ti-+1))+2£ • T — т x (ri*+1) У (ГЛ! ) s е ич • j=1 Приведенные построения производятся вплоть до момента времени тп_2 включительно. В момент времени Tn—1 = тп_2 + 3 = т0 + ( n — 1) 3т полагаем Х(тп—1 ) = x(тп—2 ) +xbaz03 . Величины у (тп_1), z (т~1) находим как решение задачи математического программирования: (у (тп-1) - Ут )2 + (z (т-11 ) - zT )2^ min. vbaZ ( t ) = m d2xbaz dt2 d ybaz При ограничениях T Т Иx (Тп-1 ) , У (Тп-1 )) +£ • т ”-1 ^ z(Тп-1 ) ^ T - т i T -т. ^ Р (x (Тп-1 ) , У ( Тп-1 )) +2£ • т n-1 , T -т i dt d2z baz dt2 ' x (Тп-1 V х у (тп-1L s ^ СХ- j=1 В момент времени тп = T полагаем x(Тп ) = Хт, У (Тп ) = Ут, z (Тп ) = ZT - Массивы данных x (Т0 ) , x (Т1 ) ,■■■, x (Т;.) ,•••, x (Тп-1 ) , x (Тп ) , У (Т0), У (Т1)-, У (тг),-, У (тп-1), У (тп), Z (Т0 ) , Z (Т1 ) ,’”, Z (т.) ,-", Z (Тп-1 ) , Z (Тп ) аппроксимируются полиномами x = xbaZ ( t ), У = Уbaz (t ), Z = ZbaZ ( t ), t £[t0,T] достаточно высокой степени. Построенные полиномы могут претендовать на то, чтобы составить базовый кинематический закон полета точки. В случае, если не все фазовые ограничения полета будут выполнены, следует увеличить п - число полуинтервалов разбиения отрезка времени [ t0, T ]. Начальное базовое положение и начальная базовая скорость точки находятся из условия xbaz0 ' 0 1 rbaZ 0 = ybaz 0 = ybaZ ( t0 ) , X ZbaZ 0 J X ZbaZ ( t0 )J xbaz 0 ' xbaZ (10 Г rbaZ 0 = ybaz0 = ybaZ ( t0 ) , X ZbaZ 0 J 1 ZbaZ ( t0 )J Базовое программное управление Vbaz (t), tе[to, T] определяется по формуле +k • dxbaz IX dt ।2+ Y + d 12 dt dt • f dx dxbaZ dt dУbaz .dt dZbaZ + +m 0 . X-g ) Алгоритм решения задачи себя также проверку равенства r ( t, t0, rbaZ 0, rbaZ 0, 1 включает в xbaZ ( t ) vbaZ (•))= Уb,z. (t) , ZbaZ ( t ) J 3. Численный эксперимент Проиллюстрируем алгоритм построения базового закона движения и базового программного управления на конкретных числовых данных. Принимаем, что m = 100 кг, t0 = 0 c, T = 10 c, кг м k = 0.45 — , g = 9.8 — , мс x* = 2400 м, xT = 3000 м, £ = 100м, p(x,y) = = 50 • sin (0.000005 • x • у) м, p(0,0) = 0. 3D график функции (p приведен на рис. 1. Число запрещенных областей полагается равным двум, т. е. что s = 2. Сами запрещенные области имеют вид У > g1 (x) = = 0.001( x -1000)(x - 500) м}, G2 Il yJ y < gi (x) = = -0.001 ( x - 2500) ( x - 2000) м}. Расположение областей G и G на плоскости Oxy показано на рис. 2. Рис. 2. Запретные области на плоскости Oxy обозначена в - окрестность множества Gj., j = 1,2 . В расчетах полагается в = 10 м. Аппроксимация наработанных массивов производится полиномами 25-й степени. В пакете Mathematica это команда Fit[dataY,{rO, t, Г2,ГЗ. Г4, Г5, Гб, Г7,Г8, Г9, Г10, Г11, Г12, Г13, Г14, t1^1^17^^^^^ . На рис. 3 приведен график базового закона движения точки по координате x . Заметим, что цель Рис. 3. График базового закона движения точки по координате x лежит вне областей G{ и G2, т. к. gx (xT)< 0, а g2 (Хт ) > 0 . Принимаем n = 200. Вычисляем Из графика видно, что этот закон является линейным. На рис. 4 приведен график базового закона движения точки по координате y . 3 = T = J0_ = 0.05 (с), n 200 xbaz 0 x3000 T = 300 |м|, l с J rji * * x * I xbaz0 = 8 ( с ), Рис. 4. График базового закона движения точки по координате y rjn * 3 0.05 = 160. В процессе решения задачи ческого Лx(Ti+1) iУ (Т+1) программирования £ |J Gj усиливается j=i математи-условие условием Х (т+1) У (Т+1) £ U (Gj ) , где символом (Gj ) j=i Из графика видно, что в процессе полета точка не заходит в запрещенные зоны. На рис. 5, 6 производится уточнение графиков на тех промежутках времени, на которых проекция точки на ось y , близко подходит к запрещенным областям и в них не заходит. Рис. 5. Уточненный график базового закона движения точки по координате y в окрестности первой запрещенной области Рис. 8. График базового закона движения точки по координате z на этапе снижения Рис. 6. Уточненный график базового закона движения точки по координате y в окрестности первой запрещенной области На рис. 7 приведен график базового закона движения точки по координате z . Рис. 7. График базового закона движения точки по координате z Из рис. 7 видно, что полет точки происходит в требуемой вертикальной полосе вплоть до момента времени T* = 8 с . Потом точка начинает снижаться. На рис. 8 показано, что в дальнейшем точка летит строго над землей, и в конечный момент времени T = 10 с она достигает ее поверхности. Промах по цели для базового закона движения составляет величину Ybaz = ( xbaz ( T)- XT )2 + + (ybaz ( T )-yT ) +(zbaz ( T )-ZT ) 2 = 0.75 м Вычисляем начальные условия для точки, определяющие базовый закон движения: (X xbaz0 f Xbaz ( 0 П f 0 ' ybaz 0 l zbaz 0 > f xbaz 0 = ybaz ( 0) = l zbaz( 0L f Xbaz ( 0 П 1.17 ^111.12 ) f 300 Л ( м ), ybaz 0 l zbaz 0 > = ybaz( 0) = l zbaz ( 0 )) -58.82 i 70. , f м ^ l с J Базовое программное управление вычисляется по формуле (3). На рис. 9–11 приведены по координатные графики базового управления. Рис. 9. График координаты vxбазового программного управления Рис. 10. График координаты vyбазового программного управления Рис. 11. График координаты vzбазового программного управления Проверка выполнения условия (4) производится непосредственно, и оно выполняется. 4. Дифференциальные уравнения динамики возмущений Следуя схеме, описанной в первом пункте, введем в рассмотрение дополнитель- ное управление u (•) = ( Ux ^ uy (•) lUz GW входящее в дифференциальные уравнения движения точки аддитивно основному управлению. Тогда уравнения (2) принимают вид k2221 x =--\X + У + z x 4—(Vx + Ux), mm y = -—Jx2 + y2 + z2 y + -1 (v + и ), m myy(5) k222 z =--Vх + y + z z 4--(vz 4 UZ )- g, mm t e[10.T]. Заменой P1 = X. P2 = У. P3 = z. P4 = X. P5 = y, Рб = z, v1 = vx , v2 = vy , v3 = Vz , U1 = Ux , U2 = Uy , U3 = Uz нормализуем систему (5). В результате получим pl = P 4 p 2 = P5 p3 = P 6 k 222 P4 =- Л/ P4 +P5 +P 6 ’ P4 + m + - ( vl + U1 ) , m k 222 P5 =- Л/P4 + P5 + P6 ’ P5 + m + — ( V 2 + U 2 ) , m k 222 P 6 =- *V P 4 + P5 + P 6 ’ P 6 - g + m + — ( V3 + U 3 ) (6) m В новых переменных базовый закон движения и базовое программное управление будут иметь вид ' Pbaz 1 (tГ Pbaz 2 ( t ) 'xbaz(t)' ybaz (t) Pbaz(t ) = Pbaz 3(t ) Pbaz 4 ( t ) = zbaz(t ) xbaz (t) Pbaz 5 ( t ) ybaz (t) lPbaz6 (t), l zbaz (t )j vbaz ( t ) = ' vbaz1 ( t Г vbaz2 ( t ) l Vbaz 3 (t )J Vbazx (t ) vbazy(t ) lVbaz (t )j t£[ t 0. T ]- Линеаризуем систему (6) в окрестности пары "базовое программное управление– базовое движение". В результате получим систему линейных дифференциальных уравнений: x = A (t) x + Bu, t g[to,T], x = x2 x3 x4 x5 < x6 > U = u1 u A (t )v 6 x 6, B ^ 6 x 3 u относительно шестимерного фазового вектора x G R6, для которого x ( t ) ~ 5P ( t ) = Pvoz (t )- Pbaz (t ) , t G [ t0, T1 ] . Здесь ■ 0 A (t )= 00 1 0 0 00 0 1 0 00 0 0 1 ^( P ' P 4 ) dP 4 ^( Р ' P 4 ) dP 5 ^(Р ' P4 ) dP 6 ^ Р ' P 5 ) dP 4 ^(Р ' P5 ) dP 5 ^(Р ' P5 ) dP 6 ^(Р • P6 ) £(Р ' P6 ) £(Р ' P6 ) P = — B = — m k — m ^ 0 < 0 'Vp 4 + p5 + p6 , , t g[10,T], T< T * — момент совмещения возмущенного движения с базовым законом. На рис. 12–17 продемонстрировано, что в рамках численного эксперимента, описанного в пункте 3, динамика фазового вектора линейного динамического объекта (7) на промежутке времени [t0, T ], T = 1 с практически тождественна динамике возмущений Рис. 12. Совместные графики координаты x линейного объекта и возмущения 5x Рис. 13. Совместные графики координаты x линейного объекта и возмущения Sy Рис. 14. Совместные графики координаты x линейного объекта и возмущения 5z Рис. 15. Совместные графики координаты x линейного объекта и возмущения 5x Рис. 16. Совместные графики координаты x линейного объекта и возмущения δy Рис. 17. Совместные графики координаты x линейного объекта и возмущения δz Заключение В статье решена задача построения базового кинематического закона движения управляемой материальной точки в однородном поле тяжести в среде с сопротивлением, пропорциональным квадрату скорости. Построенное базовое движение удовлетворяет фазовым ограничениям, наложенным на полет точки: горизонтальная проекция точки не может заходить внутрь заданных областей, а сама точка должна находиться в заданной вертикальной полосе над поверхностью земли. Построено базовое программное управление точкой, реализующее ее базовый закон движения. В численном эксперименте показано, что динамика возмущения базового закона движения адекватно описывается дифференциальными уравнениями, являющимися линеаризацией исходных дифференциальных уравнений движения точки в окрестности пары "базовый закон движения–базовое программное управление". Таким образом, задача о совмещении возмущенного движения с базовым законом сводится к задаче наведения фазового вектора управляемого линейного динамического объекта (7) на начало координат в момент времени T< T∗ . Решение этой задачи зависит от различных факторов: характера информации, на основании которой производится назначение дополнительного управления, ограничений, налагаемых на вектор дополнительных управляющих параметров и др. В данной работе задача наведения не решается. Ее решение, в том числе и в игровой постановке, будет служить предметом дальнейших исследований.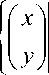
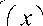
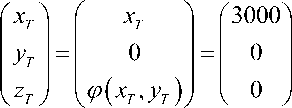

Список литературы Построение базового закона движения материальной точки и реализующего его программного управления при наличии фазовых ограничений
- Лутманов С.В. Об одной методике исследования управляемой динамической системы // Вестник Пермского университета. Математика. Механика. Информатика. 2017. Вып. 1(36). С. 13-20. EDN: YORJAZ
- Лутманов С.В., Хотько О.А. Об одной задаче управления тяжелой точкой, движущейся в среде с сопротивлением, пропорциональным квадрату скорости. // Вестник Пермского университета. Математика. Механика. Информатика. 2018. Вып. 3(42). С. 69-75. EDN: MGEWLJ
- Лутманов С.В., Хотько О.А. Оптимальная коррекция полета тяжелой материальной точки в среде с сопротивлением, пропорциональным квадрату скорости. // Проблемы механики и управления: межвуз. сб. науч. тр. Пермь, 2018. Вып. 50. С. 33-45.
- Лутманов С.В., Хотько О.А. Коррекция полета тяжелой материальной точки в среде с сопротивлением при наличии геометрических ограничений на дополнительные управления // Вестник Пермского университета. Математика. Механика. Информатика. 2019. Вып. 3(46). С. 56-64. EDN: UELTQX
- Канатников А.Н., Крищенко А.П. Терминальное управление пространственным движением летательных аппаратов // Известия РАН. Теория и системы управления. 2008. № 5. С. 51-64. EDN: JRFMYR


