Построение частотной функции Грина для свободного упругого объекта, полости которого частично заполнены жидкостью

ному уравнению и краевым условиям:

а2

—£₀Z₀(x)G(x,£) = 5(х - £) + С, ^q^ + C₂^)xq(x) ох

2) K_E<№^G(x,^

8х дхг

I =0;

-x=L

L

J G(x, ^т^ (x)dx = 0; х=0

L

J G(x,^xm₀(x)dx = 0,

(Ю)

(И)

х=0

где q(x) = т(х) + q(xx,t) ,а Cj^h С2(£) - непрерывные функции, обеспечивающие совместность совокупности соотношений (9)—(13).

Интегрируя (9) в пределах от 0 до х и учитывая граничные условия (10ц), находим

^E^x^G^ = H_xlx-^^^ J q^A-C^ J q^zdz, ^      ^                     _г=о           _г=о

где Н_х (х-^) - функция Хевисайда, обладающая следующими свойствами:

~ /0прих<£

Нх(х-^ = <

[1 при х > q.

Так как условие (Юц)выполнено, то сформулируем требования, предъявляемые к функциям

С_х (£) и С₂(£), накладываемые условием (10₂)):

£                 £

(^М+С,^) J q(z)dz + C₂«) J zq^dz, z=0                z=0

то есть,

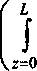
q(z)dz Cx^) +

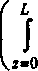
zq(z)dz C2^ =

-1.

Интегрируя (14) в пределах от 0 до х и учитывая соотношения (6) и (11ц), получаем:

E_QI₀^5-G^ = kx-^Wx-^*C_x^ J (x-z_x)q(z_x)dz_x+C₂^) J (x-z^z^dz, . (18)

^                                 z,=0z,=0

Следовательно, граничное условие (11ц) этим выражением удовлетворено. Поступая анало гично предыдущему, используя условие (И2)), сформулируем требование, предъявляемое к функциям С](^) и С2^):

££

04L-^WL-^*Cx^ J (L-z^q(z)dz*C2^) J ^"z^zq^dz .(19)

z=0z=0

Уравнение (19) совместно с (17) образуют систему двух линейных уравнений относительно неизвестных функций С_х^) и С₂(^):

$q(z> C^) +

( L        )

\zq(z]dz C₂(£) = -l,

J (L-z)q(z)dz ад) +

J (L-z)zq(z)dz C₂(f) = -(£-£),                        .

определитель которой никогда в нуль не обращается. Действительно, нетрудно показать, что

L

J q^dz-, z=0

L

J (L - z)q(z)dz;

z=0

L

J zq(z)dz z=0

L

J ^L-z^zq^dz z=0

/ z V f Z Y Z A

= J zq(z)dz - j q(z)dz j z²q(z)dz *0. (21)

Имея в виду, что функция q(z) подчиняется условиям (6), воспользуемся интегралом Стил тьеса [7]. Обозначим меру Стилтьеса интервала [О,лс] через сг(х) = J q^dz. Тогда, произведя z=0

фильтрацию входящих в q(z) 5 - функции в соответствии с известным соотношением

J 5(z -&dz = Н(х ~

А                       1 if х£с, z=0                             V         ’’ и, учитывая одностороннюю непрерывность функции Хевисайда Н(х-£) и свойства интеграла

Стилтьеса, представим (21) в виде:

( L

J dcr(z) J z²do(z] .

Д = j zda(z]

Применяем к первому члену правой части (22) неравенство Буняковского-Стилтьеса z _

J f_x^№)da^

z=0

z                z

J |/i M|² d(r(z) J |/₂(z)|² dcr(z)

z=0                z=0

здесь y](z),_/^(z)6 £2(0,!], знак равенства достигается только в том случае, когда всюду на [0,/] /j(z) = C/2 (г), где С-константа. Полагая /₁(z) = l, /₂(z) = z , получаем

J zda(z]

Таким образом, для любого иметь место

7   \z—о распределения

j dcr(z) J z²da(z) .

J\z=o 7

q^z], удовлетворяющего условиям (6), будет

Д =

J zq(z)dz

j q(z]dz J z²q(z)dz < 0.

kz=0

\z=0

Следовательно, система (20) однозначно разрешима, а функции СД^) и С2(^), делающие совместными уравнения (9) и граничные условия (10), (11), существуют и единственны. При их вычислении воспользуемся результатами работы [6]. Тогда определитель

( L            '

J q^dz

^z²q^dz =[^-М₀]

kz=o 7

Д = J zq{z)dz

и решение системы (20) имеет вид:

СХЮ =

С2(^) =

10-^:

4-^о ’

4-м<

L где М = J mQ^dz* ^pdt - полная масса «балка-жидкость»;

z=0

L           ^     _______

Д =^ + 1^ = Г m^z^dz—-ply J 4 -^12у_с -Rq) - статический момент системы «балка-z=o         ”

жидкость» относительно центра х = 0;

I_o = ^ + I^ = J z^dz^—p^Aly-by-W9p -sin20_o) + 7^(x2 ₊ ^ ^ -^ z=0

- момент инерции системы «балка-жидкость» относительно центра х = 0 (рис. 1).

Подставляя значения функций Су^) и С2(£) в уравнение (9) и дважды интегрируя по х, получаем:

G(x,^) = G1(x,^) + C3(^) + C4(^), где

G^^x-^ J ^^-^+ J 777^

_z=0 E₀I₀^ EqI^z-^

1 Ig-tA+QL+MM

2,=0     4-М₀1₀

MdCzy) dz2,(25)

C₃^ и C₄(^) - неизвестные функции, которые должны быть выбраны так, чтобы удовлетворялись граничные условия (12) и (13).

Подставляя (24) в (12) и (13), получаем следующую систему уравнений относительно С3(£) и С4(£):

L'

^С3^+^СА^) = - J Gx(x,^m0(x)dx, х=°                   ■(26)

^С₃^*^С^ = - J Gx^xm^^dx.

x=0.

Определитель этой системы совпадает с определителем системы (20), то есть ни при каком распределении q^ в нуль не обращается, следовательно, система (26) однозначно определяет зна чения величин С3(£), С4(£), обеспечивающих выполнение условий (12) и (13)

^Сз^ ⁼ l^G^^X’^ ^(0)^2 _^(0)j(0) "’oW^»

^С^ = J G_x(x,^ (₀) ₂ 1,(0)г(0) ^^W- _х=о                               ■‘о               .

Таким образом, сформулированная выше теорема доказана. Обобщенная гриновская функция рассматриваемой задачи существует, единственна, вещественна, симметрична, то есть G(x,^) = G(^,x). На квадрате (0<х, §

g^=hx^Vx^;^

+ £f 1* fc^izJl v^^D^+xz^ 2 J W(z2)    ^)2-M^

mo(z^dzA +

L f 23

4 1

Z3—£ I Z2==0

£<0^2)[z,L(Z2~Z,)

‘«-^^M

4-mi0   4 1 1

^ - (x+z₃ )Z^+xz₃M^ (z®)²-^

mQ

Зная обобщенную функцию Грина G(x,^) можно показать [2], что частотная гриновская функция существует, единственна и представима соотношением:

^^Л^ =                          ,(29)

М10-4I где Г(х,£;Л) - резольвента уравнения Фредгольма 2-го рода со статической функцией Грина G^x,^) системы в качестве нагруженного ядра

L

Г(х,£;Л) = G(x,^) + Л J G(x,z)T(z,5;Л)т0(z)dz.

z=0

Вводя итерированные ядра, соответствующие целым положительным степеням оператора G, обозначив основное ядро G(x,^) через G_x(x,^):

Gx(x,^^G(x,^-,

L

G₂(x,^ jG(x,z)G₁(z,^)_mo(z)Jz;

z=0

G^® J Gj_x(x,zyGx{z,^m0{z)dz (7=2,3,...), z=0 и используя теорему о разложении [8]

G^^p4x,^ = ^^v-^^     (Р = 2,3,...),                 (31)

получаем ряд Неймана:

Я(х,£Л)=^^-!^^-^(—)+G(z,£)+2G2(*,^^              (32)

'    и0-£ Vx) 1 51  2' 47 Й^-М ' '

Принимая во внимания соотношения (28-30) и разложение (31); суммируя появляющиеся при этом в (32) геометрические ряды, получаем аналитические зависимости частотной функции Грина от Л, в форме разложения функции 91 па простые дроби:

м0-4         ЙАГ(4-^)’ ад = V^l^l^f±1 + ^Г-’G (х,^) + чем и заканчивается решение поставленной задачи.