Построение фрактальных объектов при помощи библиотеки MPICH2

Понятия фрактал и фрактальная геометрия, появившиеся в конце 70-х гг., с середины 80-х прочно вошли в обиход математиков и программистов. Слово «фрактал» образовано от латинского fractus, в переводе означает: состоящий из фрагментов. Оно было предложено Бенуа Мандельбротом в 1975 г. для обозначения нерегулярных, но самоподобных структур, которыми он занимался. Рождение фрактальной геометрии принято связывать с выходом в 1977 г. книги Мандельброта `The Fractal Geometry of Nature'

Виды фракталов

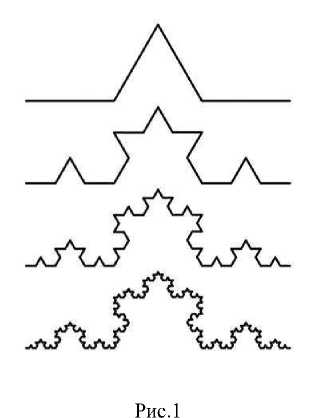
Геометрические. В двухмерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры и получается геометрический фрактал.

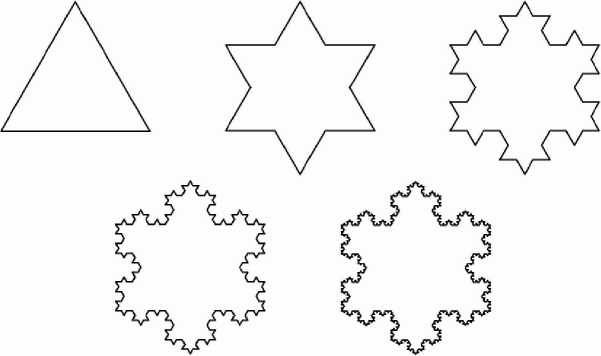
Рис. 2

Алгебраические. Получают их с помощью нелинейных процессов в n-мерных пространствах. Наиболее изучены двухмерные процессы. Интерпретируя нелинейный итерационный процесс, как дискретную динамическую систему, можно пользоваться терминологией теории этих систем: фазовый портрет, установившийся процесс, аттрактор и т.д.

Известно, что нелинейные динамические системы обладают несколькими устойчивыми состояниями. То состояние, в котором оказалась динамическая система после некоторого числа итераций, зависит от ее на- чального состояния. Поэтому каждое устойчивое состояние (или, как говорят, – аттрактор) обладает некоторой областью начальных состояний, из которых система обязательно попадет в рассматриваемые конечные состояния. Таким образом фазовое пространство системы разбивается на области притяжения аттракторов. Если фазовым является двухмерное пространство, то окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет этой системы (итерационного процесса).

Рис. 3                               Рис. 4

Стохастические. Получаются в том случае, если в итерационном процессе случайным образом менять какие-либо его параметры. При этом получаются объекты очень похожие на природные: несимметричные деревья, изрезанные береговые линии и т.д. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря.

Рис. 5

Рис. 6

Методы построения фрактальных объектов.

L-systems. Понятие L-систем ввел Аристрид Линденмайер, в основном, для изучения формальных языков. В дальнейшем выяснилось, что с помощью них можно строить самоподобные фракталы. Алгоритм, реализующий L-системы в графическом виде, получил название turtle-графика (по-английски turtle – черепаха). Подробнее о L-системах можно посмотреть в книге: P.Prusinkiewicz & J. Hanan, Lindenmayer Systems, Fractals, and Plants, Lecture Notes in Biomathematics, N79, Springer-Verlag, New-York, 1989.

«Черепаховый» алгоритм представляет собой интерпретатор кодового слова, являющегося результатом выполнения L-системы, которое анализируется слева направо и может содержать следующие символы:

F – указывает, что «черепаха» должна сделать один шаг вперед с прорисовкой;

b – шаг вперед без прорисовки;

«+» – увеличить угол;

«-» – уменьшить угол;

«[« – открыть ветвь;

«]» – закрыть ветвь.

Пример исходных данных для фрактала кривая Коха:

Аксиома: F ;

Правило: F ^ F - F + + F - F ;

Угол: — .

Системы итерирующих функций(IFS). Метод «Систем Итерируемых Функций» (Iterated Functions System – IFS) появился в середине 80-х гг. как простое средство получения фрактальных структур.IFS представляет собой систему функций из некоторого фиксированного класса функций, отображающих одно многомерное множество на другое. Наиболее простая IFS состоит из аффинных преобразований плоскости:

X ' = A * X + B * Y + C

Y ' = D * X + E * Y + F

Пример исходных данных для фрактала кривая Коха: Koch{

0.3333	0.0000	0.0000	0.3333	0.0000	0.0000
0.3333	0.0000	0.0000	0.3333	0.6666	0.0000
0.1667	-0.2887	0.2887	0.1667	0.3333	0.0000
-0.1667	0.2887	0.2887	0.1667	0.6666	0.0000}

Опыт построения фрактальных объектов . Для визуализации фрактальных объектов и подсчета фрактальной размерности была разработана программа Планиметр-стереометр. В ней были реализованы методы: IFS, L-systems, координатный и построение с помощью turtle графики. Изначально код был адаптирован для систем с последовательной обработкой данных.

Инициатор

*      "

Построение ломаная 1

Построение ломаная 1.1

Построение ломаная 1.2

Построение ломаная 2

i

Схема 1

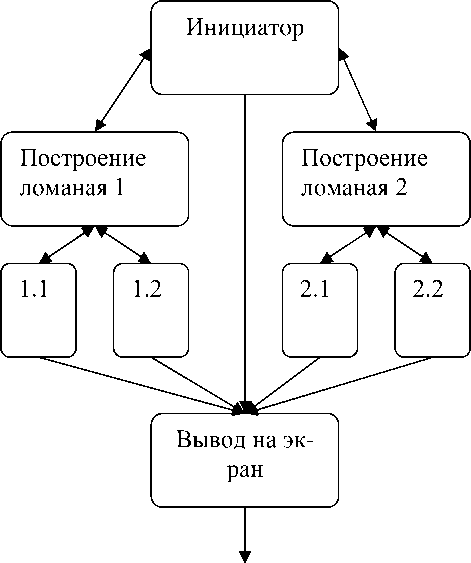
Схема 2

Организация параллельности вычислений, когда в один и тот же момент выполняется одновременно несколько операций обработки данных, осуществляется, в основном, за счет введения избыточности функциональных устройств ( многопроцессорности ) [1]. В этом случае можно достичь ускорения процесса решения вычислительной задачи, если осуществить разделение применяемого алгоритма на информационно независимые части и организовать выполнение каждой части вычислений на разных процессорах. Подобный подход позволяет выполнять необходимые вычисления с меньшими затратами времени, и возможность получения максимально-возможного ускорения ограничивается только числом имеющихся процессоров и количеством «независимых» частей в выполняемых вычислениях.

Параллельная модель программирования:

• 1)    параллелизм данных;

• 2)    параллелизм задач.

Подход, основанный на параллелизме данных, характеризуется тем, что:

• •    одна операция применяется сразу к нескольким элементам массива данных. Различные фрагменты такого массива обрабатываются на век-

• торном процессоре или на разных процессорах (ядрах) параллельной вычислительной системы;

• •    обработкой данных управляет одна программа;

• •    пространство имен является глобальным;

• •    параллельные операции над элементами массива выполняются одновременно на всех доступных данной программе процессорах.

Подход, основанный на параллелизме задач, характеризуется тем, что:

• •    вычислительная задача разбивается на несколько относительно самостоятельных подзадач. Каждая подзадача выполняется на своем процессоре;

• •    для каждой подзадачи пишется своя собственная программа на обычном языке программирования (С++, Fortran и т.д.);

• •    подзадачи должны обмениваться результатами своей работы, получать исходные данные. Практически такой обмен осуществляется вызовом процедур специализированной библиотеки. Программист при этом может контролировать распределение данных между различными процессорами и различными подзадачами, а также обмен данными.

Программная реализация

MPICH2 – это быстродействующая и широко портируемая реализация стандарта MPI (реализованы оба стандарта MPI-1 и MPI-2). Цели создания MPICH2 следующие:

• 1.    Предоставить реализацию MPI, которая эффективно поддерживает различные вычислительные и коммуникационные платформы, включая общедоступные кластеры (настольные системы, системы с общей памятью, многоядерные архитектуры), высокоскоростные сети (Ethernet 10 ГБит/с, InfiniBand, Myrinet, Quadrics) и эксклюзивные вычислительные системы (Blue Gene, Cray, SiCortex).

• 2.    Сделать возможными передовые исследования технологии MPI с помощью легко расширяемой модульной структуры для создания производных реализаций.

При построении фрактала – кривая Коха был использован подход, основанный на параллелизме данных. Процедура формирования генератора фрактального объекта требует 3 параметра (координата начала, угол наклона «черепашки», масштаб), а алгоритм построения генератора остается прежним.

1 итерация

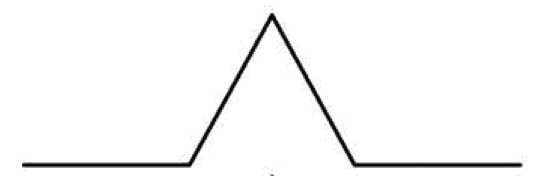
Рис. 7. 1 процесс

Рис. 8. Порождены 4 параллельных потока

3 итерация

Рис. 9. Порождены 16 параллельных потоков

Реализация данного алгоритма проводилась с компьютерами на базе процессоров Intel Celeron E3300(2 ядра) и Intel Core 2 Quad(4 ядра). Повышение скорости алгоритма на базе 2-х ядерного процессора составила 1,87 раза относительно однопоточного приложения, а на базе 4-х ядерного процессора – 3,68 раза.