Построение фреймовой модели перевода с использованием кластеризации термов

Важным этапом в IP-переводе (машинном переводе, использующем ресурсы информационно-поисковых систем) на стадии синтеза является сопоставление исходного текста (ИЯ-текста) и релевантных текстов на целевом языке (ЦЯ-текстов), выявление в них схожих сегментов. Процесс такого сопоставления выполняется в несколько шагов:

• 1)    сегментация текста;

• 2)    кластеризация сегментов;

• 3)    построение фреймовой модели структуры текста.

Рассмотрим каждый шаг подробнее.

Сегментация текста. Для анализа структуры предложений ИЯ- и ЦЯ-текстов необходимо поделить эти предложения на логические сегменты, где каждый сегмент будет семантически самостоятельной единицей. Сегментом назовем непрерывный фрагмент тек- ста, состоящего из термов одного языка, обозначающих связанную по некоторому критерию группу понятий. Составными частями сегмента могут быть термы следующих видов:

• -    объект ( obj );

• -    субъект ( sub );

• -    действие ( do );

• -    свойство (pro );

• -    связь ( con ).

Идентификация составных частей сегмента осуществляется после проведения стемминга, когда установлена принадлежность термов к тем или иным частям речи. Определяется, что объект ( obj ) и субъект ( sub ) являются существительными, действие ( do ) -глаголом, свойство (pro ) - прилагательным, а связь ( con ) включает в себя все знаки пунктуации, предлоги, союзы и частицы.

Выделение сегментов можно производить несколькими методами. Рассмотрим наиболее эффективный метод сегментации - сегментацию через связь ( con ). В основе данного метода лежит предположение о том, что семантические скопления термов в ИЯ- и ЦЯ-предложениях отделены друг от друга связями ( con ) - знаками препинания, предлогами, союзами и частицами [1].

Таким образом, при каждом возникновении связи ( con ) происходит трансформация семантической структуры, возникает новый сегмент текста, несущий новую семантику. Следовательно, для осуществления сегментации текста необходимым и достаточным является наличие словаря служебных частей речи и словаря знаков препинания. Механизм сегментации через связь ( con ) для фрагмента предложения « The goal of integrating syntactic information into translation model... » приведен на рис. 1.

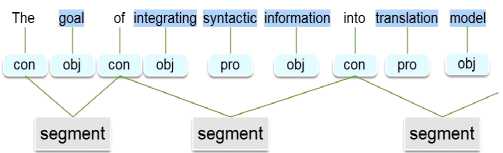
вид:

Рис. 1. Сегментация через связь ( con )

Кластеризация. Для управления полученными сегментами применяется фреймовая модель представления знаний, где каждый терм сегмента описывается соответствующим фреймом. Однако для формирования такой модели предварительно необходимо сгруппировать имеющиеся в сегментах термы в кластеры -группы термов со схожими свойствами. Рассмотрим несколько алгоритмов кластеризации.

Для каждого вида термов (obj, sub, pro, do, con) определен ряд характеризующих их признаков. Так, для термов obj, sub и pro такими признаками являются «род», «число» и «падеж», для термов do - это «время», «вид» и «залог», а для термов con отличительными признаками являются свойства «предлог», «союз» и «пунктуация». Каждый из этих признаков, в зависимости от типа терма, принимает определенные значения. Например, свойство «род» может принимать одно из трех значений [мужской, женский, средний], а свойство «вид» - всего два значения [совершенный, несовершенный] и т. д. Данные значения берутся в качестве критериев кластеризации - деления на группы в зависимости от принимаемых значений. Для формализации значений термов сопоставим каждому значению числовую меру. Так, например, значениям [мужской, женский, средний] сопоставим значения [1, 2, 3], а значениям [совершенный, несовершенный] - значения [1, 2] и т. д. Таким образом, данные числовые значения играют роль расстояний между свойствами термов. Функция расстояния между двумя свойствами xt и xj записывается как L(Xj, xj) и обладает следующими признаками.

Неотрицательность расстояния:

L(X,xj) ^ 0.(1)

Симметрия:

L (X, X) = 0.(2)

Неразличимость тождественных свойств:

L(X, xj) = L(xj, x).

Неравенство треугольника:

L(x,Xj) < L(x,xk) + L(xk,Xj).(4)

Если все свойства термов x , , x ₂,..., x_n представить в виде матрицы данных X размером p х n

	X 11	X 12	x 7 ... x n
X	X 21	X 22	... X 2 n	= ( x 1 , x 2,.„, x n ),    (5)

X , Л' п p 1 p ^

то расстояния L(x,, x,) могут быть представлены в виде матрицы расстояний, имеющей симметричный

Чем больше мера L ( x , , x , ), тем больше отличие в свойствах термов, а, следовательно, возрастает и вероятность принадлежности термов к разным кластерам. И наоборот, чем меньше значение L ( x , , x , ), тем больше вероятность того, что термы принадлежат одному кластеру.

Расстояние L ( x , , x , ) может быть вычислено несколькими способами.

Общая формула геометрического расстояния в многомерном пространстве, т. е. расстояния Минковского, определяется по формуле

L p ⁽ x , ^x j ) =| Ё| ^x k , , — ^x k , , Г I ,             ⁽⁷⁾

V к = 1                 )

где d - размерность пространства; p - количество значений, принимаемое признаками.

Частным случаем геометрического расстояния между несколькими значениями свойств того или иного терма является евклидово расстояние. Его формула приведена ниже:

Г d                 2 1 1/2

L 2 ⁽ X, x j ) = Z ( xM - x k , j )      .

Следующий тип расстояния – манхэттенское (сити-блок, хэмминговское) расстояние:

d

L i ⁽ x . x j ) = E K - - x k j .            (9)

k = 1

Однако манхэттенское расстояние обычно применяют при наличии дихотомических свойств (свойств, имеющих два значения). А так как некоторые свойства термов могут принимать более чем два значения, то такой тип расстояния является непригодным для кластеризации термов ИЯ- и ЦЯ-текстов.

Еще одним типом расстояния является супремум-норма (расстояние Чебышева):

• L „ ⁽ X , x j ) = suP {| x k .I" x k,j } .              ⁽¹⁰⁾

Анализ рассмотренных типов расстояния показал, что для задачи кластеризации сегментов ИЯ- и ЦЯ-текстов пригодными являются расстояние Чебышева и евклидово расстояние [2].

Построение фреймовой модели структуры текста. После того как исходный и целевые тексты разбиты на сегменты и проведена кластеризация термов для всех сегментов, строится фреймовая модель пред- ставления полученной структуры (см. таблицу). Для каждого вида термов – obj, sub, pro, do, con – определяется одноименный вид фрейма, хранящий информацию о свойствах связанного с ним терма.

Структура фреймов, используемых при построении шаблонов

Имя фрейма	Идентификатор, присваиваемый фрейму, уникальный в данной фреймовой системе ( obj , sub , pro , do , con )
Слоты	Свойства фрейма, принимающие значения из некоторого диапазона
Демоны	Автоматически запускаемые процедуры. Выполняются при осуществлении каких-либо действий над слотом: IF-NEEDED – указывает, какое действие необходимо выполнить если значение вставляется в пустой слот. IF-ADDED – указывает, какое действие необходимо выполнить при добавлении в слот значения. IF-REMOVED – указывает, какое действие необходимо выполнить при удалении значения из слота

Все свойства термов хранятся в слотах фрейма и имеют строковый тип данных. Так, например, для фрейма do , описывающего термы-глаголы определено три слота: время, вид и залог. При обработке терма-глагола формируется экземпляр фрейма do , а свойства терма записываются в слоты. Результат записи может выглядеть следующим образом: время – прошедшее, вид – несовершенный, залог – активный.

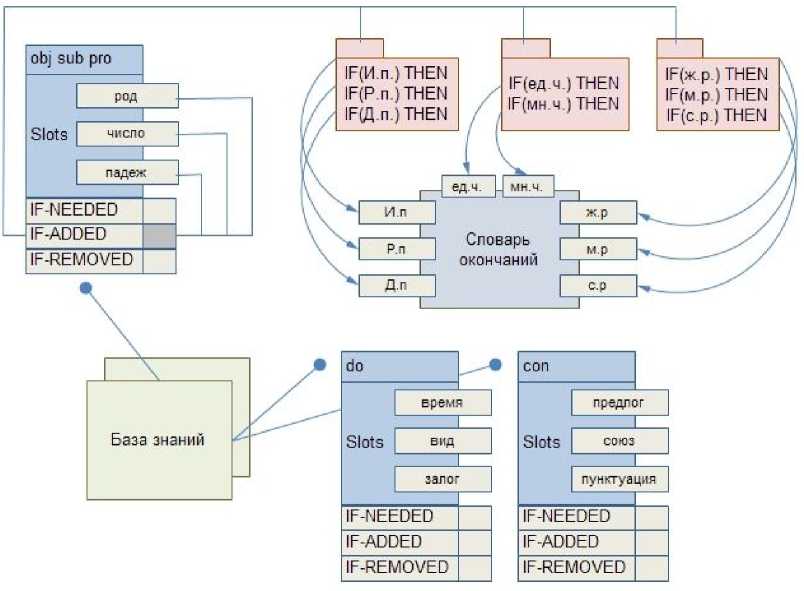
Рис. 2. Фреймовое представление знаний

Описание структуры фрейма. Сразу после добавления свойств терма в слоты соответствующих фреймов происходит вызов демона IF-ADDED , запуск которого осуществляется при каждой очередной вставке значения в тот или иной слот. Демон IF-ADDED , в зависимости от того, каким фреймом он был вызван, вызывает соответствующую процедуру приведения значения свойства терма, хранящегося в слоте к форме на целевом языке.

Так, например, при вставке в слот «число» значения «множественное» демон IF-ADDED вызовет процедуру преобразования формы терма из множественного числа исходного языка к множественному числу целевого языка. Для этого преобразующая процедура обращается к имеющемуся в системе словарю окончаний для пары «ИЯ–ЦЯ». Таким образом, формируется база знаний на основе фреймового представления (рис. 2), хранящая информацию о структуре сегментов текста и термов, образующих эти сегменты.

Данная модель пригодна для осуществления сопоставления исходного и целевых текстов на этапе синтеза ЦЯ-текста в IP-системе машинного перевода, а также для выполнения посегментного перевода фраз ИЯ-текста в фразы ЦЯ-текста.

Рассмотренная фреймовая модель является эффективным средством представления знаний в IP-системе машинного перевода на этапе синтеза текста, так как позволяет управлять формой термов при переходе от исходного языка к целевому, является менее громоздкой, чем представление через нейронную сеть, и более гибкой, чем продукционное представление. Приведенный алгоритм сегментации текста через связь позволяет быстро и эффективно производить разбиение текстового массива на фрагменты, что ускоряет процесс их анализа.