Построение функции "цена - качество" на основе анкетных опросов экспертов

Учет требований рынка при формировании цены перепродаваемых объектов возможен с применением методов кластерного анализа, когда объект описывается множеством качественных И количественных характеристик, а потом в результате поиска в базе данных оцениваемый объект с той или иной степенью сходства [4] относится к какому-либо классу объектов. При этом предполагается, что классы объектов уже определены и для каждого из классов рассчитана цена. Недостатки такого подхода очевидны - методики расчета мер сходства ставят серьезные ограничения при описании объектов, сложно выбрать собственно методику расчета. И наконец, для определения цены необходимо проводить какой-то дополнительный анализ рынка.

Каждый перепродаваемый объект рассматривается продавцом и покупателем как ограниченное множество потребительских характеристик. Каждая характеристика влияет на формируемую цену в строго определенной степени. Соответствие характеристики требованиям рынка оценивается с помощью некоей шкалы. Потребительские характеристики можно разделить на количественные и качественные. Количественные задаются числом граммов, метров и секунд. Качественные - путем соотнесения характеристики с элементом шкалы. Каждый из элементов шкалы также в определенной степени оказывает влияние на цену. Процесс оценки в данном случае напоминает заполнение анкет, когда на поставленный вопрос следует выбрать один из предлагаемых ответов [8; 9]. Графически систему анкетных оценок можно представить в виде иерархии, в фокусе которой находится искомое совокупное качество (см. рис. 1).

Таким образом, совокупное качество объекта есть сумма степеней влияния каждой из его потребительских характеристик, выраженных через отношение к элементам множества шкал оценок - см. (1). Цена объекта находится в прямой зависимости от его совокупного качества. Если известна рыночная цена какого-либо объекта и можно определить его потребительские качества, то, зная потребительские качества другого объекта, легко определить его цену - см. (2), (3) - причем с учетом трудно формализуемых факторов, влияющих на состояние рынка.

Вр^Н^Е,);         (1)

• Е,    с \e.i-ei2--eA

где В_р - совокупное качество объекта, H_i - числовой вес вклада z-й характеристики в совокупное качество объекта, N - количество возможных характеристик (качеств), Ej - шкала для оценки z-й характеристики, е_у - j-я оценка из z-й шкалы, к - количество элементов е_у в шкале Е_Г

Для расчета вероятной цены продажи осуществляют следующие действия:

К = С%?            (2)

С_р = КхВ_р,             (3)

где С_а - известная цена уже проданного объекта, В_а - совокупное потребительское качество уже проданного объекта, К - переходной коэффициент, В_р - совокупное потребительское качество оцениваемого объекта, С_р - вероятная цена продажи оцениваемого объекта.

Переходной коэффициент К в таком случае является линейной аппроксимацией функции

C=f(B,D, V);

В е D;                    (4)

В с В„, где D - множество неучтенных потребительских характеристик, V - множество случайных факторов, воздействующих на

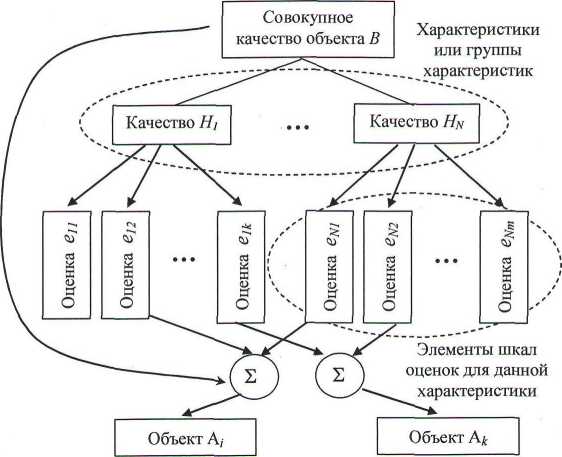
Рис. 1. Иерархическое представление системы анкетной оценки

внешнюю среду, и/или множество нефор-мализуемых потребительских характеристик, В - множество всех возможных величин В_р.

Если мощность множества случайных факторов V не может быть уменьшена в силу самого его свойства, то уменьшение мощности множества D возможно за счет увеличения мощности множества В. Это достигается путем увеличения количества Д и Ej, т. е. уточнения и усложнения анкеты. Совпадение множеств В и D для объектов реального мира, как правило, невозможно из-за большой размерности D.

Экстремальные значения В_р в рамках построенной системы анкетных оценок можно найти как сумму минимальных (максимальных) е для каждого качества Н.

В_т™ = Е min^,.

⁸m,x = Е ^{m axE}r

B_min и B_mox описывают соответственно наихудший и наилучший по своим потребительским характеристикам объекты. Влияние множеств V и D может проявиться в том, что объект с B_min {В_тах) не будет обладать минимальной (максимальной) реальной ценой. Следует отметить, что распределение величин В на числовой оси в общем случае не будет равномерным.

Максимальную мощность множества В можно определить путем перемножения количества к элементов шкал Е;.

z_ = Ц ^к^ (5) где Z_max - количество возможных уникальных (не повторяющихся) значений В к, - количество элементов в z-й шкале, N - количество шкал Е; или рассматриваемых в данной системе характеристик (качеств).

Поскольку для расчета совокупного потребительского качества оцениваемого объекта В используется арифметическое суммирование, а также округление величин Н, и Е^ то возможна ситуация совпадения величины В_р для нескольких уникальных комбинаций потребительских характеристик. Вводится величина Z, которая всегда будет меньше или равна Z_max. Расчет величины Z возможен только путем перебора, что легко алгоритмизируется и реализуется с помощью компьютера.

Таким образом, значение Zmax описывает количество возможных групп, к которым могут быть отнесены оцениваемые объекты, a Z - количество реально полученных в данной системе оценок групп. Подразумевается, что объекты внутри группы (кластера) являются равноважными, т. к. у них совпадает величина Вр, т. е. они равны по своим потребительским характеристикам. Если же, по мнению эксперта, при совпадении величины Вр потребительские характеристики разнятся, следует создать новую группу (уменьшить мощность множества D) путем добавления новых характеристик и шкал или новых элементов шкал для оценки старых характе- ристик. Значения Bmax, Bmin, Zmax и Z при этом изменятся.

На рис. 2 представлен обобщенный случай линейной аппроксимации зависимости цены от качества в рамках рассматриваемой методики [9; 10]. Линия а представляет собой реальную зависимость, которая существует на рынке. Эта линия может быть получена только в том случае, когда для всех возможных групп объектов будет установлена реальная цена продажи С_а и рассчитаны величины В_а. В таком случае может быть получено множество К переходных коэффициентов K_i с мощностью Z;

^ ^G {^minp )’—’ ^i ’•¹ •' ^max(7J } .

Формулы (2) и (3) предлагают усечение множества К до одного элемента (рис. 2, точки Са,Ва,К—К^. Аппроксимирующая прямая Ь, проведенная через точку К и начало координат, позволяет получить множество точек {С^,Сй,С3,Ср,СеУ Интервал Delta между точками К^ и К представляет собой погрешность аппроксимации, т. е. расхождение между реальной ценой Стах объекта с потребительскими качествами Bmax(Z) и ошибочной ценой Се, рассчи танной на основании формул (2) и (3). Уменьшение интервала Delta возможно путем накопления, с последующей статистической обработкой, эмпирически полученных значений VKmin,K'2,KQ,K3,Kp,K^, и, следовательно, превращения линии b в кривую более высокого порядка. К сожалению, полное совпадение кривых а и b практически невозможно. Объясняется это тем, что, помимо множеств D и V, существенное влияние на конечную продажную цену оказывает округление цены продавцом до копеек, рублей, десятков, а то и сотен и тысяч рублей, в то время как расчет Ка и Ва возможен с любой практически достигаемой точностью.

Точки (В'₂, C'J и (В₂₃,С₃) характеризуют ситуацию, когда Zmnx. Например, точка В_{2 3} описывает два объекта с непов-торяющймися комбинациями потребительских характеристик, у которых в результате суммирования по формуле (1) совпали числовые значения В_р. В общем случае утверждается, что интегральный показатель качества В₂₃ однозначно определяет цену С₃. В частном - такое совпадение может означать неправильно построенную систему опроса (анкету). Как уже отмеча-

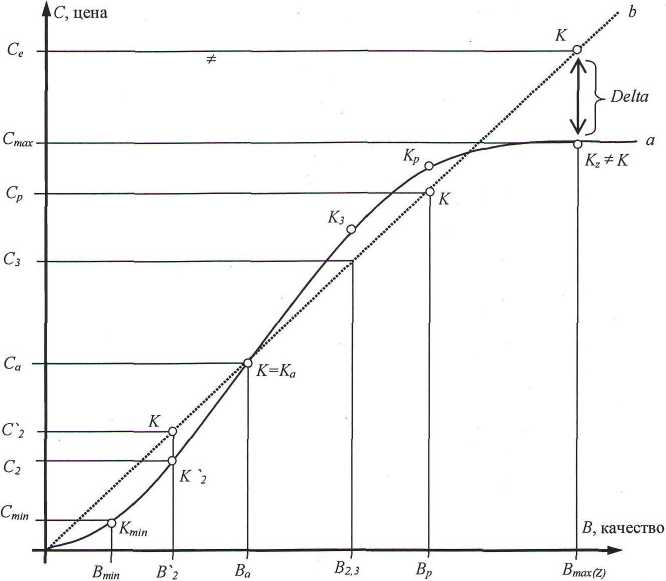
Рис. 2. Линейная аппроксимация зависимости C_p=f(B,D, V)

лось выше, уточнение анкеты приведет к появлению новой группы объектов с числовым значением В = В'₂, что даст возможность определить новую цену С₂ через коэффициент К, либо если цена С₂ определена эмпирически, - получить новый элемент множества К - коэффициент К'₂.

Значения К, Н^ e_t и В_р однозначно определены на множестве положительных действительных чисел:

к— -5->я⁺; (6)

H„e,-^R*-, (7) b_p-^r*. (8)

В качестве способа отображения F₂ использовалась методика парных сравнений, предложенная Т. Саати [1; 2; 3]. Существуют альтернативы, которые имеют количественные характеристики, например, такие как габариты или масса. В этом случае не имеет смысла проводить парные сравнения, а отображение F₂ следует заменить процедурой линейного нормирования [5]. Линейное нормирование заключается в том, что количественные величины заполняют собой вектор W’— VW]',w₂',..,w^ }, где п - число альтернатив, aw'.- количественная величина. Затем вектор W нормируется и в результате получается вектор приоритетов B^fc{w_;,w₂,..,w_n}, где w^w^./S, S- сумма количественных оценок:

S^^V (12)

Причем, если мы ищем лучшую альтернативу с наибольшей величиной данной характеристики, то вектор нормируется непосредственно с этими количественными оценками, а если наоборот (чем меньше данная величина, тем лучше), то каждый элемент вектора W заменяется на обратную ему величину и только после этого происходит нормирование.

Отображение F₃ представляет собой так называемый иерархический синтез. Он заключается в перемножении весов вышележащих элементов иерархии на веса связанных с ним нижележащих [1 - 5; 7].

Процесс построения графической модели предметной области, а также отображений F2 и F3 является извлечением из экспертных знаний по данной проблематике и осуществляется однократно. Подобная работа может быть выполнена как вручную, так и с помощью специализированных программных средств [4; 6; 7]. Аппроксимирование отображения А, осу ществляется в зависимости от требуемой точности либо простым усреднением коэффициента К, либо статистической обработкой множества К тем или иным методом. Полученные веса элементов шкал могут быть занесены в базу данных, а сам процесс заполнения анкет автоматизирован. В этом случае эксперту-оценщику предоставляется экранная форма со списком вопросов, а напротив каждого вопроса располагается комбинированный (выпадающий) список возможных ответов. Веса ответов автоматически суммируются, по базе данных определяется переходной коэффициент и рассчитывается вероятная цена продажи.

Подобная система оценок разработана для определения стоимости вторичного жилья, перепродаваемого на жилищном рынке г. Волгограда, и подержанных автомобилей ВАЗ [8].