Построение графа знаний по телекоммуникационным данным

Термин граф знаний (ГЗ) определяется как база знаний, состоящая из сущностей и связей между ними. ГЗ широко используются в обработке естественного языка, вопросно-ответных системах, рекомендательных системах и т.д. [1]. ГЗ содержат структурированные данные о сущностях и связях между ними, представленные в формате триплета (h,r,t), где h — головная сущность, — отношение, — хвостовая сущность. ГЗ востребованы в различных областях, включая и телекоммуникации [2], где они используются для описания сетевых устройств, сервисов, бизнес-процессов и других сущностей, связанных с телекоммуникационной инфраструктурой [3]. Актуальность применения ГЗ в этой области обусловлена несколькими факторами [4]:

• ■    рост объёма и сложности телекоммуникационных данных, которые требуют эффективного управления, интеграции и обработки.

• ■    необходимость повышения качества и надёжности телекоммуникационных сервисов, а также удовлетворения индивидуальных потребностей клиентов.

• ■    появление новых технологий и стандартов в телекоммуникационной отрасли, которые создают новые возможности для телекоммуникационных операторов.

ГЗ могут помочь в решении различных задач в телекоммуникационной области за счёт использования следующих преимуществ [5]:

• ■    данные в ГЗ являются структурированными и семантичными, что позволяет извлекать, связывать и анализировать информацию из разных источников и в разных форматах;

• ■    для ГЗ возможно применение логического вывода и машинного обучения, что позволяет автоматизировать и оптимизировать процессы принятия решений, обнаружения аномалий, предсказания поведения и др.

Одним из источников данных в области телекоммуникаций являются лог-файлы биллинговых систем. При построении ГЗ на основе данных лог-файлов, в связи с их слабой структурированностью, формируемый граф часто имеет неполную структуру, в которой отсутствует нужная информация. Таким образом, разработка метода эффективного построения ГЗ по телекоммуникационным лог-файлам является перспективной областью исследований.

Целью данной работы является разработка метода построения ГЗ по телекоммуникационным данным по лог-файлам биллинговой системы, а также исследование возможности применения метода на основе подхода многошагового рассуждения для генерации интерпретируемых рекомендация по восстановлению отсутствующих связей в ГЗ.

1    Наборы данных

В ГЗ содержатся данные о сетевых устройствах и информационных системах, функционирующих в телекоммуникационной сети (ТС), и данные, содержащие информацию о биз-нес-процессах компаний. ГЗ, используемые в телекоммуникационных системах, включают бизнес-процессные, информационные, функциональные и компонентные модели, а также статистические и оперативные данные о сетях. Данные, представленные в форме ГЗ в сфере телекоммуникаций, могут использоваться для различных целей, таких как анализ, моделирование, оптимизация и управление ТС.

В работах [6, 7] рассматривается телекоммуникационный ГЗ, построенный по данным оператора кабельного телевидения. При построении ГЗ использовались данные о пользователях, сетевых устройствах и услугах оператора. Построение ГЗ позволило провести анализ поведения клиентов кабельного оператора. Важным требованием была возможность обработки большого объёма данных [7].

В [8] представлен ГЗ, построенный на основе стандартизированных для области телекоммуникаций моделей, разработкой и поддержкой которых занимается консорциум TM Forum , специализирующийся на стандартизации и управлении телекоммуникационными и цифровыми сервисами. TM Forum предоставляет фреймворк ( TM Framework, TMFF) , включающий в себя бизнес-процессную ( Enhanced Telecom Operations Map, eTOM) , информационную ( Shared Information and Data Model, SID ), функциональную модели ( Functional model) и модель приложений ( Telecom Application Map, TAM). Модель TMFF и связи между её элементами на примере задачи заказа услуг показаны на рисунке 1.

При построении ГЗ ТС операторов, как правило, используются многие источники, которые предоставляют информацию о ТС — это лог-файлы, различные текстовые описания, включая пользовательскую документацию, документацию программного кода и т.д. Объёмы таких данных достаточно большие, в частности, в [7] при построении проприетарных ГЗ (ПГЗ, закрытый граф, разработанный для решения задач конкретной сферы или предприятия) использовались лог-файлы сетевых устройств, в которые могло быть записано более миллиона сообщений в день. Однако, эти данные часто являются неполными, что приводит к нарушению полноты структуры формируемого ГЗ.

ГЗ на основе TMFF может использоваться как эталонная модель, с которой сопоставляются модели, построенные по реальным данным телекоммуникационных компаний. При формировании рекомендаций по восстановлению структуры предлагается применять подход на основе многошагового рассуждения, который обеспечит интерпретируемые прогнозы. Эталонная модель TMFF при этом используется в качестве обучающего и валидационного набора данных.

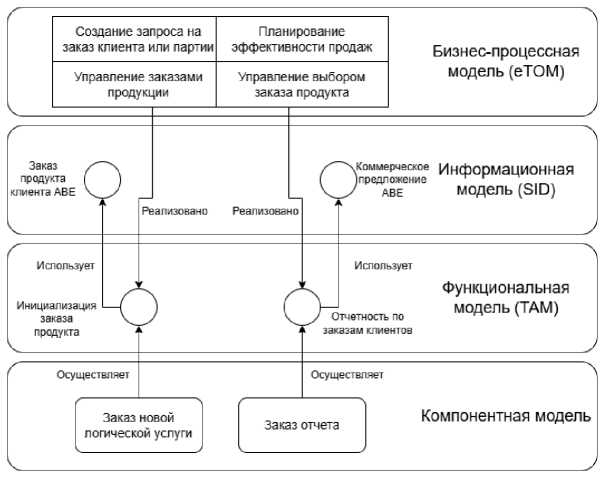
Рисунок 1 - Модель TMFF и зависимости между её элементами

2    Метод решения

Предлагаемый метод предусматривает построение ГЗ, содержащего данные о ТС и реализуемых в них процессах, на основе имеющихся о сетях данных, получаемых из различных источников, а также восстановление структуры графа с использованием многошагового рассуждения и ГЗ, построенного на основе эталонных моделей TM Forum .

• 2.1    Построение ГЗ по телекоммуникационным данным

Эталонный ГЗ был построен на основе модели TMFF , включающей в себя модели eTOM, SID, TAM и компонентную модели. С использованием этих моделей были сгенерированы файлы CSV и выполнен маппинг ГЗ в формате JSON для СУБД Neo4j . Данный ГЗ экспортирован и помещён в открытый доступ на платформе GitHub [8].

ПГЗ построен по телекоммуникационным данным, полученным из биллинговой системы. В состав ГЗ были включены данные об информационных объектах (для формирования информационной составляющей ГЗ), данные из спецификаций программного кода (для формирования бизнес-процессной и функциональной составляющих ГЗ) и данные об автотестах (для формирования компонентной составляющей ГЗ).

Данные об информационных объектах получены с помощью реляционной базы данных (БД) в результате разбора документации, который позволил выявить связи между элементами данных из БД и компонентами биллинговой системы.

По данным, хранящимся в БД, построена проприетарная онтология, которая в дальнейшем интегрирована в единый ПГЗ. Для преобразования данных из БД в онтологию использовался редактор онтологий Protege , в частности функция импорта R2RML . Для создания файлов маппинга сущностей БД использовались следующие классы: имя БД ( Database name ), имена таблиц ( Table names ), имена столбцов ( Column names ) и имена ключей ( Key names ). Иерархия классов онтологии представлена на рисунке 2.

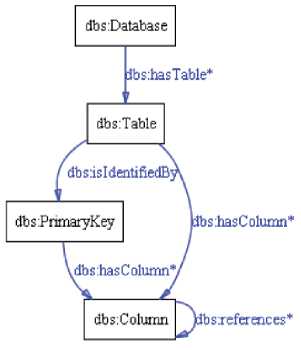
Рисунок 2 – Иерархия классов проприетарной онтологии

Для построения компонентной модели, включаемой в состав ПГЗ, использовались лог-файлы, полученные в результате выполнения автотестов. Были проанализированы лог-файлы и сформированы CSV файлы, содержащие информацию об иерархии компонентов биллинговой системы. Информация о бизнес-процессах и функциях была получена путём автоматической обработки исходного кода. На основе этой информации был построен ПГЗ с использованием СУБД Neo4j .

Связи между элементами функциональной и информационной моделей в ПГЗ показаны на рисунке 3.

Примеры связанных сущностей, соответствующих функциям «Извлечение данных баланса» из проприетарной функциональной модели и «Централизованное управление правилами заказа» из эталонной функциональной модели, а также элементы из связанных с ними сущностей информационной модели показаны на рисунках 4 и 5. На рисунке 6 отображены связи между сущностью «Заказы логических услуг», соответствующей проприетарной информационной модели, и сущностями, соответствующими SID.

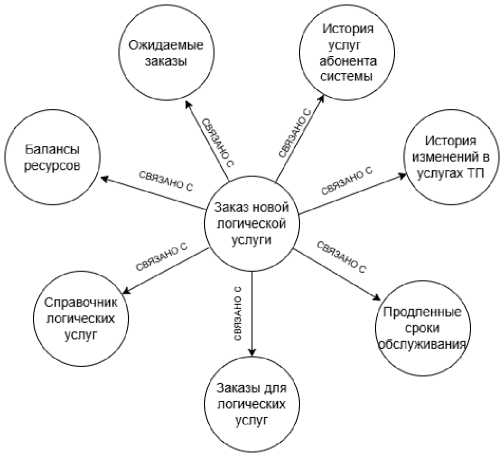
Рисунок 3 – Фрагмент графа знаний, показывающий связи между элементами функциональной и информационной моделей

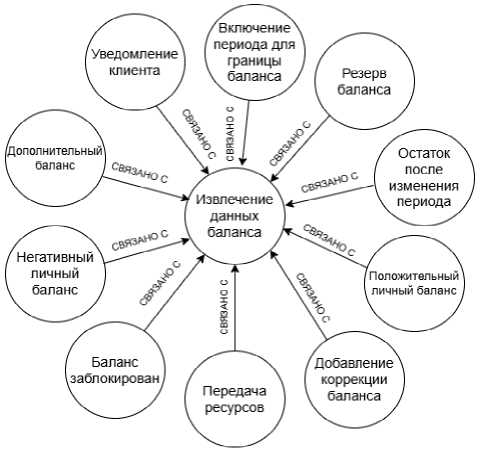
Рисунок 4 – Пример связанных сущностей, соответствующих функции « Извлечение данных баланса » из проприетарной функциональной модели

• 2.2    Восстановление структуры ГЗ

Дальнейшим этапом является восстановление структуры полученного ПГЗ. Восстановление структуры ГЗ – это задача прогнозирования недостающих связей или фактов в ГЗ [9], необходимость решения которой обуславливается тем, что значительная часть создаваемых ПГЗ является неполными и зашумленными, что ограничивает их полезность и надёжность [10]. Для восстановления структуры ГЗ предлагается использовать методы, способные выводить новые факты из существующих и заполнять пробелы в ГЗ, в частности, метод многошагового рассуждения.

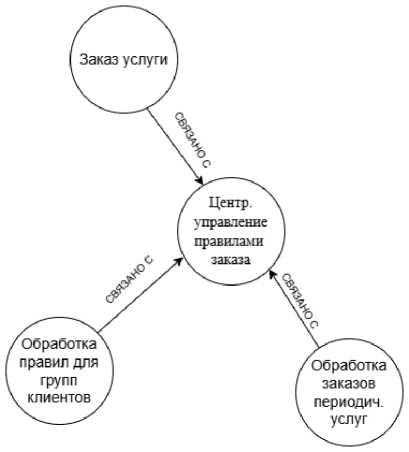
Рисунок 5 – Пример связанных сущностей, соответствующих функции « Централизованное управление правилами заказа » из эталонной функциональной модели

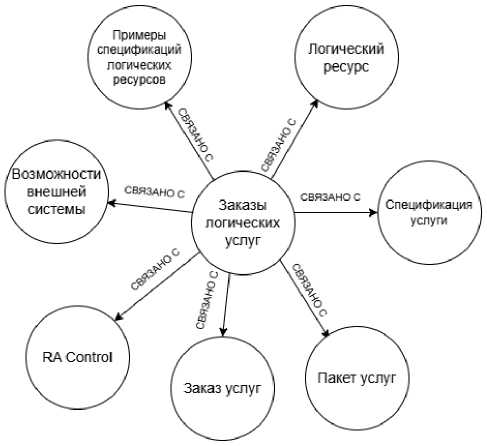
Рисунок 6 – Фрагмент графа знаний с связанными сущностями, соответствующими информационным моделям эталонного и проприетарного графов знаний

• 2.2.1    Многошаговое рассуждение

• 2.2.2    Предложенное решение

Многошаговое рассуждение – это подход, позволяющий предсказывать новые связи для неполных ГЗ, который заключается в поиске и комбинировании нескольких логических шагов, связывающих сущности и отношения [11]. При многошаговом рассуждении вместо того, чтобы предсказывать хвостовую сущность t для данного триплета запроса (h,r), обеспечивается предоставление доказательного пути от ℎ до , который демонстрирует процесс вывода [12].

Многошаговое рассуждение помогает восстановить отсутствующие элементы ГЗ, используя косвенные связи и выполняя интерпретируемые логические выводы на основе доступных данных, что особенно актуально для телекоммуникационных ГЗ, построенных по лог-файлам и другим данным телекоммуникационных операторов, которые имеют неполную структуру [7]. Интерпретируемость полученных результатов позволяет обосновывать прогнозы и принимать взвешенные решения, что важно при решении прикладных задач.

Применение подхода многошагового рассуждения для ПГЗ в связке с эталонным ГЗ, построенным по модели TM Forum , позволяет предоставить рекомендации по восстановлению структуры ГЗ телекоммуникационного оператора. Для этого модель на основе многошагового рассуждения обучается на эталонном ГЗ. Рекомендации формируются за счёт предсказания недостающих связей в ПГЗ.

Многошаговое рассуждение может быть реализовано с помощью различных методов, которые предполагают использование моделей, основанных на обучении с подкреплением [13, 14], нейросетевой архитектуре трансформера и других [15]

Предлагаемый метод основан на многошаговом рассуждении, которое использует архитектуру трансформера кодер-декодер для преобразования запроса в доказательный путь (« sequence-to-sequence» ).

Использование такой архитектуры обеспечивает существенные преимущества [16]:

• ■    метод не полагается на существующие связи для создания доказательного пути и обладает гибкостью для восстановления отсутствующих связей (особенно эффективно при работе с разреженными ГЗ);

• ■    доказательные пути, генерируемые предлагаемым методом, обеспечивают интерпретируемость результатов.

Разработанный метод рассматривает многошаговое рассуждение как задачу преобразования последовательностей из одного домена последовательности в другой. Запрос является исходной последовательностью, а доказательный путь — целевой. Кодер-трансформер отображает запрос и предыдущую последовательность путей в контекстуализированное представление, и это представление затем используется для авторегрессионного декодирования выходного пути, токен за токеном.

Идея предлагаемого метода состоит в том, чтобы свести задачу многошагового рассуждения к задаче ответа на вопрос с использованием обработки естественного языка. Различные сущности и отношения интерпретируются как разные слова, контекстуальные вложения которых обучаются на графе.

Процесс обучения предлагаемого метода:

q = ⁽h,r)     = = (rt , ti ,^,r_n,t,[eos]),

где [eos] - конец токена последовательности, q и т обозначают запрос и путь. Разложение вероятности:

|т|

Р №) = П P(-^Tk\d’<

к=1 где т_к обозначает к -й токен выходного пути, а |т| - количество токенов в пути.

Обучается матрица встраивания токенов Е Е К ^Vxd , где d — размерность векторного представления. Размер словаря равен V = |8| + |^| + |S|, поскольку словарь токенов включает в себя набор сущностей Е, набор отношений R и набор специальных токенов S. При декодировании маска позволяет кодировщику обрабатывать только токены запроса ( h ) и предыдущие токены в выходном пути, предотвращая раскрытие будущей информации.

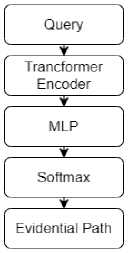
Рисунок 7 - Se-quence-to-sequence метод

Далее метод вычисляет распределение вероятностей для к -го токена как:

Р (' |Q ,^т < /с) = $°f t^т o([MLP[E пc(h, г, <_{с к} )) • Е),

где М L Р( ) — многослойный перцептрон, Ес с ( ) — кодировщик ( Transformer Encoder ) предлагаемого « sequence-to-sequence » метода (рисунок 7).

В процессе обучения метод выбирает конкретный путь для каждого триплета (h, r,t) ЕТ из всех возможных путей между h и t с максимальной длиной (V = 3. Значение N было выбрано на основе наблюдения, что большинство пар сущностей в наборах данных ГЗ связаны максимум за 3 шага. Этот выбор также обеспечивает корректное сравнение с аналогами, которые также ограничивают максимальную длину пути до 3 [15]. В качестве функции потерь используется перекрёстная энтропия с дополнительным сглаживанием меток.

3    Исследование свойств решения

В ходе эксперимента построены эталонный ГЗ и ПГЗ. Параметры построенных ГЗ приведены в таблице 1.

Для оценки качества предлагаемого метода на основе многошагового рассуждения рассчитаны следующие метрики: средний обратный ранг (MRR) и количество попаданий в N. MRR — это показатель, используемый для оценки эффективности системы ранжирования в задачах поиска информации и рекомендаций [17]. Он измеряет среднее качество ранжиро- ванных результатов, учитывая ранговую позицию первого релевантного элемента. MRR рассчитывается путём взятия обратной величины ранга первого релевантного элемента и после- дующего усреднения этих обратных рангов по всем запросам:

∑                               ( )

где — общее количество запросов, а      — позиция наиболее релевантного для запро- са элемента в первых N результатах.

Количество попаданий в N ( H@N ) — метрика оценки, используемая в системах информационного поиска и рекомендаций [18]. Она измеряет долю запросов, по которым хотя бы один реле-

Таблица 1 – Ключевые параметры и значения построенного эталонного и проприетарного графов знаний

Параметры	Значения эталонного графа знаний	Значения проприетарного графа знаний
Количество сущностей	10458	2882
Количество связей	30708	3040

вантный элемент появляется в первых N результатах: |{  ∈            ≤  }| H@N = —-—-----

( )

В таблице 2 представлены метрики, рассчитанные на построенном эталонном ГЗ для су- ществующих решений и предлагаемого метода.

Таблица 2 – Результаты прогнозирования отношений на эталонном графе знаний

Метод	MRR	H@1	H@3	H@10
TransE	0,426	0,321	0,471	0,633
ConvE	0,437	0,343	0,432	0,627
RotatE	0,423	0,314	0,473	0,626
TuckER	0,452	0,358	0,494	0,635
ConE	0,448	0,342	0,492	0,641
KG-BERT	-	0,041	0,301	0,422
Seq-to-seq	0,439	0,324	0,462	0,619

Таким образом, разработанный метод практически достигает тех же результатов, что и методы, основанные на векторных представлениях. Результаты метрик предложенного метода « sequence-to-sequence » превысили результаты метода KG-BERT . При этом использование предложенного метода обеспечило интерпретируемость, в то время как результаты, получаемые с использованием других методов, интерпретируемыми не являются.

Заключение

В результате проведённого исследования построены эталонные ГЗ и ПГЗ. Для создания эталонного ГЗ применялись модели TM Forum , а ПГЗ строился за счёт автоматизированной обработки лог-файлов автотестов и таблиц БД биллинговой системы.

Разработанный на основе многошагового рассуждения « sequence-to-sequence » метод для восстановления структуры ГЗ рассматривает триплет запроса и доказательный путь как последовательности и использует архитектуру трансформера. Предложенный метод имеет хорошую сходимость и возможность интерпретации результата.

Авторский вклад

Головин А.А. построил ГЗ, провел исследование, участвовал в написании рукописи. Жукова Н.А. спланировала исследование и структуру ГЗ, участвовала в написании рукописи.