Построение хранилища обобщённых вычислительных экспериментов на основе онтологического подхода

Математическое моделирование реальных физических процессов в большинстве случаев предполагает проведение серий вычислительных экспериментов (ВЭ), в рамках которых изучается состояние модели и особенности её поведения в различных диапазонах изменения входных переменных и параметров модели. С развитием средств вычислительной техники и технологий параллельных вычислений появилась возможность построения обобщённого ВЭ (ОВЭ), основная идея которого состоит в многократном решении прямой или обратной задачи численного моделирования для различных наборов значений параметров моделирования [1]. Подобный подход позволяет получить решение не для одной, а для класса задач математического моделирования, заданного в многомерном пространстве параметров модели- рования. В результате появляется возможность одновременно исследовать влияние нескольких параметров на интересующие характеристики модели, в том числе исследовать их совместное влияние в различных сочетаниях диапазонов изменения.

Целью проведения ОВЭ, как правило, является определение либо уточнение характеристик и свойств моделей: поиск функциональных зависимостей или закономерностей для прогнозирования исследуемых характеристик, определяемых результатами моделирования; сравнение точности моделей, а также установление границ областей, в которых определённая модель даёт более точные результаты по сравнению с другими. Известны примеры успешного применения ОВЭ при решении задач вычислительной гидродинамики [1, 2], газовой динамики [3, 4], автоматизации проектирования энергетических установок [5].

При переходе к ОВЭ значительно возрастают объём и размерность обрабатываемых массивов экспериментальных данных. Моделирование реальных физических процессов на основе проведения серии экспериментов со всеми допустимыми комбинациями моделей и параметров моделирования, как правило, не представляется возможным. Поэтому актуальной является задача адаптивного управления ОВЭ.

В работе [6] предложен подход к планированию ОВЭ с возможностью динамической корректировки плана на основе оценки результативности промежуточных состояний ОВЭ. Под планом ОВЭ понимается последовательность экспериментов, подлежащих проведению, для заданного многомерного массива значений параметров моделирования с выбранными методами анализа и интерпретации результатов эксперимента.

Преимуществом динамического планирования ОВЭ является возможность сокращения объёма недостаточно результативных экспериментов и, напротив, обеспечение более детального экспериментального исследования тех диапазонов значений входных данных и параметров моделирования, где требуется подтверждение и уточнение найденных закономерностей. Процедуру планирования целесообразно делать интерактивной, привлекая к ней исследователя и обеспечивая возможность совместного использования традиционных методов обработки экспериментальных данных и методов их интеллектуального анализа, например, визуально-когнитивной аналитики [2, 7, 8].

Для обеспечения автоматизации и программной поддержки методов адаптивного планирования и управления ОВЭ требуется организация хранения результатов ОВЭ и сценариев его проведения. Актуальной задачей является разработка методов и технологий построения хранилища данных ОВЭ. Его создание обеспечит возможность повторного использования экспериментальных данных и результатов их обработки, а также организацию библиотек и репозиториев моделей анализа данных по различным направлениям и классам проблем. Необходимо обеспечить простой и интуитивно понятный механизм взаимодействия пользователя с хранилищем, возможность формирования запросов в терминах предметной области (ПрО). Данная возможность может быть обеспечена за счёт использования онтологического подхода.

В статье рассматриваются особенности хранения данных, связанных с ОВЭ, предлагаются модели данных для построения хранилища ОВЭ, способ построения онтологии ОВЭ, и рассматриваются пути её применения для организации доступа к хранилищу и эффективного взаимодействия с ним пользователя.

1    Формализованное представление ОВЭ

Для формирования требований к структуре хранилища ОВЭ и выделения сущностей, которые должны быть положены в основу моделей представления данных, необходимо выпол- нить формализацию понятия ОВЭ, а также связанных с ним понятий состояния и плана ОВЭ. С учётом результатов работы [6] предлагается следующая схема формализации.

• 1.1    Понятие и структура данных ОВЭ

Пусть математическая модель исследуемой системы задана набором:

< X, Y , A , F >, (1) где X = ( x 1 , x ₂, ..., x_L ) - вектор входных переменных, L - количество входных переменных, Y = (У 1 ,У 2 , •-, У м ) — вектор выходных переменных, M - количество выходных переменных, A = { a 1 , a ₂, ..., a N } - множество параметров моделирования, также называемых определяющими параметрами [1], N - количество определяющих параметров, F - реализуемое с помощью модели отображение пространства входных переменных в пространство выходных переменных. Вид данного отображения определяется структурой модели с учётом её определяющих параметров из множества A.

В качестве определяющих параметров моделирования могут выступать как числовые величины (например, некоторые физические характеристики исследуемого процесса), так и качественные показатели, такие как используемые численные методы, характеристики программно-аппаратного обеспечения и др. [2, 3].

Каждый параметр ak характеризуется областью допустимых значений Vk (к = 1, ...,N). Для числового параметра это может быть диапазон изменения, а для нечислового - множество возможных значений. На значения параметров могут быть наложены совместные ограничения вида gt(ai, a2, „., aN), t = 1, „., T, (2) которые могут задаваться в форме уравнений, неравенств или логических условий. Совокупность областей значений параметров вместе с набором ограничений вида (2) задаёт N-мерное пространство определяющих параметров V, которое в общем случае является подмножеством декартова произведения областей значений каждого параметра:

V с V 1 X V 2 X ... Vn . (3)

Поскольку ОВЭ предполагает решение задачи моделирования при вариации определяющих параметров на некотором дискретном наборе точек пространства этих параметров, то на области V k значений каждого параметра a k выбирается множество значений W k = { a k 1 , a k ₂, • •., a_k , _pk }, для каждого из которых выполняется моделирование. Здесь й ц - конкретные выбранные значения параметра a_k , j = 1, ..., p_k , где p_k- число таких значений для параметра a_k . В простейшем случае для числового параметра W_k может представлять собой набор равноотстоящих точек внутри диапазона его значений.

Разбиение пространства определяющих параметров представляет собой множество всех возможных кортежей выбранных значений каждого параметра, принадлежащих пространству параметров V , т.е. удовлетворяющих ограничениям (2):

W = ( W 1 X W 2 X ... Wn ) n V . (4)

Любая точка, принадлежащая данному разбиению, задаёт определённый набор значений определяющих параметров, участвующий в проведении ОВЭ:

W i = ( a i, i i , a 2, i 2 , ..., a N , iN ), a k , ik ^e W k . (5)

В качестве примера можно рассмотреть ОВЭ для трёхмерной задачи невязкого обтекания конуса [4]. Для данного ОВЭ определяющими параметрами являлись: число Маха ( a 1 ), угол полураствора конуса в градусах ( a 2 ), угол атаки в градусах ( a 3 ). В качестве W k были выбраны следующие множества значений определяющих параметров: W 1 = {3, 5, 7}; W ₂ = {10, 15, 20};

W 3 = {0, 5, 10}. Соответственно, w i в данном случае представляют собой упорядоченные тройки элементов этих множеств: w ₁ = (3, 10, 0); w ₂ = (3, 10, 5); „.; w ₂₄ = (3, 20, 10) (для комбинации углов полураствора и атаки, равных 10°, ВЭ не проводились).

C учётом введённых обозначений одиночный ВЭ характеризуется дискретным векторным полем ES , которое задаёт распределение Y* значений вектора выходных переменных Y для заданного множества X значений вектора входных переменных X при некотором фиксированном наборе w * значений определяющих параметров, принадлежащем разбиению W :

ES = < X, Y* >,(6)

где

Y* = { Y = F (X, w*), X е X}.(7)

ОВЭ ( EGen ) характеризуется N -мерным массивом, элементы которого задают дискретные векторные поля, соответствующие одиночным ВЭ для всех элементов разбиения W :

EGen = < x, y, w >,( где

Y = { Y = F (X, w), X е X, w е W}.(9)

Полученный массив многомерных данных содержит первичные результаты ОВЭ и не может рассматриваться как решение задачи моделирования. Поэтому далее выполняется его обработка с целью получения полезной для исследователя информации об объекте моделирования и выявления закономерностей и взаимосвязей, присущих определяющим его параметрам. Для этого могут использоваться традиционные методы обработки экспериментальных данных и методы интеллектуального анализа данных , а также совместное использование различных подходов и методов.

Таким путём, от первичного многомерного массива экспериментальных данных, задаваемого набором (8), осуществляется переход к обобщённым показателям, которые представляют собой результаты обработки первичных данных. Эти показатели используются далее для интерпретации, поиска закономерностей, формирования и проверки гипотез. Примерами обобщённых показателей могут служить главные компоненты в задачах понижения размерности, нормы векторов ошибок L1 и L2 в задачах оценивания точности различных численных методов при варьировании определяющих параметров моделирования [3, 4] и др.

• 1.2    План и состояние ОВЭ

План ОВЭ должен задавать:

• 1)    серию одиночных ВЭ, которые требуется провести для заданного множества X значений входных переменных и выбранного разбиения пространства определяющих параметров W ;

• 2)    множество обобщённых показателей для представления результатов обработки и анализа первичных экспериментальных данных, а также набор используемых для этого методов.

План ОВЭ можно представить в виде:

< X , W , C , H >,                                 (10)

где C = { C ₁, C ₂, ..., C S } - множество обобщённых показателей, H - отображение пространства первичных экспериментальных данных в пространство значений обобщённых показателей. Вид данного отображения определяется применяемыми методами обработки и анализа первичных данных.

Состояние ОВЭ определяется совокупностью ВЭ, проведённых в соответствии с выбранным планом, и задаётся многомерным массивом экспериментальных данных, получен- ных при текущем разбиении пространства определяющих параметров, набором значений обобщённых показателей, полученных в результате обработки данного массива, а также множеством закономерностей, выявленных на основе анализа и интерпретации этих значений. Состояние ОВЭ можно представить в виде:

< X Y , W , C(W) , R >, (11) где C(W) - пространство значений множества обобщённых показателей C , полученное при разбиении пространства определяющих параметров W ; R - множество выявленных закономерностей.

2    Проектирование структуры хранилища ОВЭ

В контексте задачи построения хранилища, ОВЭ можно рассматривать как набор проведённых одиночных ВЭ и историю изменения планов их проведения. Для хранения набора одиночных ВЭ может быть использован традиционный подход к представлению многомерных экспериментальных данных, основанный на двумерных таблицах. В этом случае часть столбцов таблицы описывает значения определяющих параметров, а другая часть - значения выходных переменных для разных моделей. Это обусловливает первую особенность хранения ОВЭ - возможность использования традиционных подходов к хранению многомерных данных. Хранить значения входных переменных в подобной таблице нецелесообразно, поскольку эти значения могут быть недостаточно структурированными и создавать избыточность данных. Вместе с тем, эти значения должны содержаться в хранилище. Это обусловливает вторую особенность хранения ОВЭ - нецелесообразность табличного хранения значений входных переменных в единой таблице со значениями определяющих параметров и выходных переменных. Значения выходных переменных образуют многомерные массивы большого объёма, но при этом они не используются для анализа результатов напрямую -вместо них используются обобщённые показатели. Данный аспект обусловливает третью особенность хранения ОВЭ - нецелесообразность хранения значений выходных переменных ВЭ в единой таблице со значениями определяющих параметров и обобщённых показателей. Целесообразно хранить их отдельно при условии сохранения связи с соответствующим одиночным ВЭ.

При хранении ОВЭ необходимо хранить и историю изменения планов проведения ВЭ. Это связано с тем, что после проведения части запланированных ВЭ возможна корректировка плана ОВЭ, т.е. создание новой последовательности проведения ВЭ, которая может иметь общие части с прошлыми планами и не иметь таковой. В общем случае имеется множество пересекающихся последовательностей одиночных ВЭ, и для их хранения целесообразно использовать соответствующие структуры данных, например, графовые. Это обусловливает четвёртую особенность хранения ОВЭ - целесообразность хранения истории изменений планов проведения ОВЭ в виде графовых структур.

После проведения очередной серии ВЭ оценивается состояние ОВЭ, анализ которого используется при формировании решения о дальнейшем плане проведения ОВЭ. В этой связи состояние ОВЭ можно рассматривать как характеристику проведённой серии последовательных одиночных ВЭ и сопоставлять её с последним экспериментом в данной серии. Это обусловливает пятую особенность хранения ОВЭ - необходимость хранения состояния ОВЭ после каждой проведённой серии экспериментов.

Для организации эффективного хранения данных, связанных с ОВЭ, важно учитывать специфику операций, которые будут осуществляться с ними. К таким операциям относятся добавление, редактирование, удаление и поиск (выборка). Операции поиска (выборки) в первую очередь используются для анализа состояния ОВЭ, что служит основой управления

ОВЭ. Хранение и обработка многомерных данных зачастую строится на базе реляционных систем управления базами данных (СУБД) и OLAP¹ -хранилищ.

Традиционные хранилища показывают высокую эффективность сбора и выборки данных, но обладают рядом недостатков при представлении данных [9], среди которых ключевыми для рассматриваемой задачи являются следующие.

• ■    Хранение только детализированных данных. Для обеспечения большей нормализации и, как следствие, более быстрого доступа к данным, информация максимально детализируется, однако для последующего их анализа такой подход неудобен ввиду большого объёма дополнительной информации.

• ■    Хранилище может содержать данные в разных форматах. Данное обстоятельство существенно затрудняет анализ данных без их предварительной обработки.

• ■    Доступ к данным пользователей осуществляется на основе заранее составленных запросов. Такой подход не может обеспечить гибкость в выборе данных для анализа.

При хранении данных ОВЭ использование технологий OLAP приведёт к дополнительной избыточности, создаваемой структурой базы данных. При построении хранилища следует использовать современные реляционные СУБД, позволяющие проводить необходимую нормализацию отношений между сущностями с целью снижения избыточности и обеспечения целостности данных [10]. В модели данных для хранения ОВЭ целесообразно предусмотреть отдельные таблицы для описания входных переменных, определяющих параметров, выходных переменных и обобщённых показателей, а также отдельные таблицы для хранения полученных в ходе проведения экспериментов значений входных переменных, определяющих параметров, выходных переменных и обобщённых показателей. Для хранения значений выходных переменных нет необходимости проводить нормализацию, поэтому эти данные могут храниться в сериализованной форме в виде текста с использованием форматов JSON (или XML ) или же в виде ссылки на объект (файл) во внешнем хранилище (например, в S3 -хранилище [11]). Для этого может быть создана отдельная таблица, связанная с таблицей, описывающей одиночные ВЭ.

Для хранения больших объёмов экспериментальных данных можно использовать специальные иерархические форматы, например, HDF5 [12]. Особенность данного формата состоит в том, что каждый файл имеет свою внутреннюю структуру, и это может быть более эффективным (по сравнению с форматами JSON или XML ) в случае, когда требуется обмениваться данными с другими системами (например, системами визуализации экспериментальных данных). Формат HDF5 позволяет получать данные в виде массива, при этом встроенные средства анализа отсутствуют. С использованием данного формата можно построить автономное хранилище, части которого можно легко отделить, что делает его удобным инструментом для транспортировки данных.

Учёт четвёртой особенности хранения ОВЭ приводит к наличию сущности или сущностей для хранения истории изменения планов проведения ОВЭ. Вводится понятие «родительского» плана ОВЭ, под которым понимается начальный план проведения серии ВЭ. Если в ходе его выполнения или после завершения возникает потребность в проведении другой серии ВЭ, то формируется новый план, который должен ссылаться на «родительский» план и на последний проведённый ВЭ «родительского» плана. Новый план может также послужить «родительским» для другого плана. Для того, чтобы хранить такие структуры в базе данных , следует организовать иерархию путём добавления в таблицу с описанием планов проведения ВЭ ссылки на другую запись этой же таблицы с ограничением в виде запрета ссылки на себя. Если в таблице отсутствует ссылка на «родительский» план, то данная запись связана с вер- шиной иерархии, т.е. с первичным планом проведения серии ВЭ. Описание такой таблицы планов должно включать номер начального ВЭ «родительского» плана. С помощью подобной иерархии планов и структуры таблиц представляется возможным восстановить полную историю проведения ОВЭ с учётом всех изменений.

Поскольку данные, описывающие состояния разных ОВЭ, могут иметь различные типы и размерность, то хранить состояния ОВЭ целесообразно также в сериализованном виде с использованием форматов JSON или XML . Для обращения к данным, хранящимся в подобных объектах, можно использовать встроенные в СУБД языковые механизмы запросов. Для хранения состояния ОВЭ можно добавить соответствующее поле в таблицу одиночных ВЭ, что позволит хранить состояние ОВЭ после каждого проведённого ВЭ.

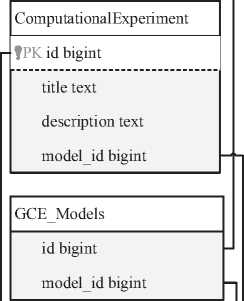
Модель базы данных, которая может быть положена в основу организации хранилища ОВЭ, с учётом рассмотренных выше особенностей, представлена на рисунке 1.

GeneralizedComputationaExperiment

PKid bigint title text description text

GCE_Plans id bigint plan_id bigint

ComputationalExperimentsPlan

PKid bigint start_experiment_number bigint

ComputationalExperimentsPlanLists plan_id bigint experiment_id bigint

Model id bigint title text description text

GCE_PlannedExperiments id bigint experiment_id bigint

GCE_Experiments id bigint experiment_id bigint

RawOutputResults

PKid bigint store_type mood data text url text

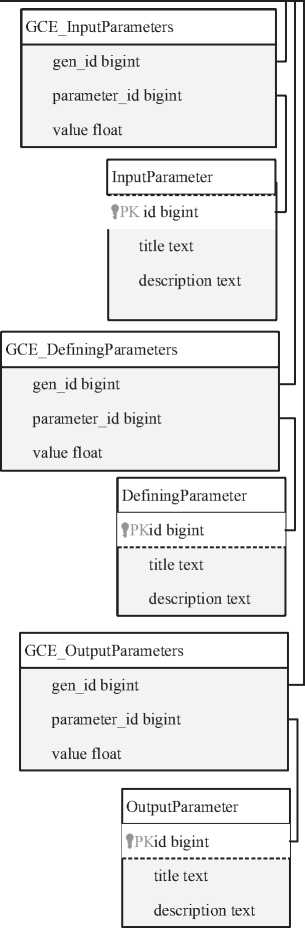
Рисунок 1 – Модель базы данных для организации хранилища ОВЭ

Механизм доступа пользователя к информации по ОВЭ с целью её анализа должен учитывать специфичный для ПрО механизм поиска, группировки и структурирования данных, а также принятую в соответствующей ПрО терминологию. В качестве основы для такого механизма предлагается использовать методологию онтологического инжиниринга. Онтология в рассматриваемой задаче позволяет:

• ■    добавлять в хранилище дополнительную мета-информацию об ОВЭ (это обеспечивает возможность дополнять описание хранимых данных, что может быть учтено при построении более эффективных методов обработки соответствующих данных, например, указывать типы данных, используемых для конкретных параметров).

• ■    формировать запросы и структуры данных при выборке (например, запросы пользователя, составленные через некоторый упрощённый человеко-машинный интерфейс, можно преобразовывать в физические запросы к хранилищу, либо уточнять уже существующие запросы [13], либо после получения данных из хранилища приводить к виду, удобному для понимания и последующего анализа).

Поиск и структуризацию данных исследователю удобнее выполнять в терминах той ПрО, к которой относится ОВЭ, а для этого в онтологии предусмотрен соответствующий тезаурус с синонимами, учитывающий в том числе и языковые особенности терминов [14].

3    Онтологическая модель ОВЭ

Онтологическая модель ОВЭ, инвариантная к ПрО, с поддержкой тезауруса ключевых понятий позволяет формировать мета-описание ОВЭ, включая сопоставление терминов, набор сущностей и их типов данных. Мета-описание может использоваться для формирования запросов к хранилищу в упрощённой форме, скрывая от исследователя детали физической реализации хранилища. Для разработки онтологической модели ОВЭ были выделены следующие ключевые сущности (понятия).

• 1)    ОВЭ. Является базовым понятием создаваемой онтологии. Связано с остальными понятиями.

• 2)    Модель . С учётом (1), под моделью поднимается отображение, с помощью которого на основе значений входных переменных и с учётом значений определяющих параметров формируются значения выходных переменных и/или обобщённых показателей.

• 3)    Одиночный ВЭ. С учётом (6) и (7), это понятие объединяет данные, включающие в себя значения выходных переменных, полученные для заданного набора значений входных переменных и определяющих параметров с помощью выбранной модели.

• 4)    План ОВЭ. В рамках онтологической модели под планом понимается серия одиночных ВЭ в определённом порядке их следования, а также набор правил обработки первичных экспериментальных данных и представления результатов этой обработки в виде значений обобщённых показателей.

Предполагается, что исследователь при проведении ОВЭ будет оперировать в первую очередь перечисленными ключевыми понятиями. Смысл одних и тех же понятий для исследователей из разных ПрО может отличаться, поэтому в онтологическую модель были включены понятия синоним, язык и ПрО. Словарь синонимов для используемых в онтологии понятий составляется для конкретной ПрО. При этом остаётся возможным использовать один и тот же синоним для различных ПрО (например, смежных). Разработанная обобщённая онтологическая схема ОВЭ представлена на рисунке 2.

Помимо неопределённости, связанной с трактовкой понятий ПрО, неопределённость может также возникать при описании самих компонентов онтологической модели. Описания на разных языках отличаются, например, русскоязычному термину «Обобщённый вычисли- тельный эксперимент» соответствует англоязычный термин «Generalized computational ex-periment». Разные термины могут использоваться для описания одного и того же понятия внутри одного языка. Например, понятие «модель» в зависимости от ПрО может иметь целый ряд синонимов: функция, алгоритм, мутация, версия и т.д. Фрагмент разработанного тезауруса для некоторых ключевых понятий, входящих в онтологическую модель ОВЭ, представлен в таблицах 1 и 2. Использование исследователем привычных для него терминов повышает эффективность хранения, проведения и управления ОВЭ.

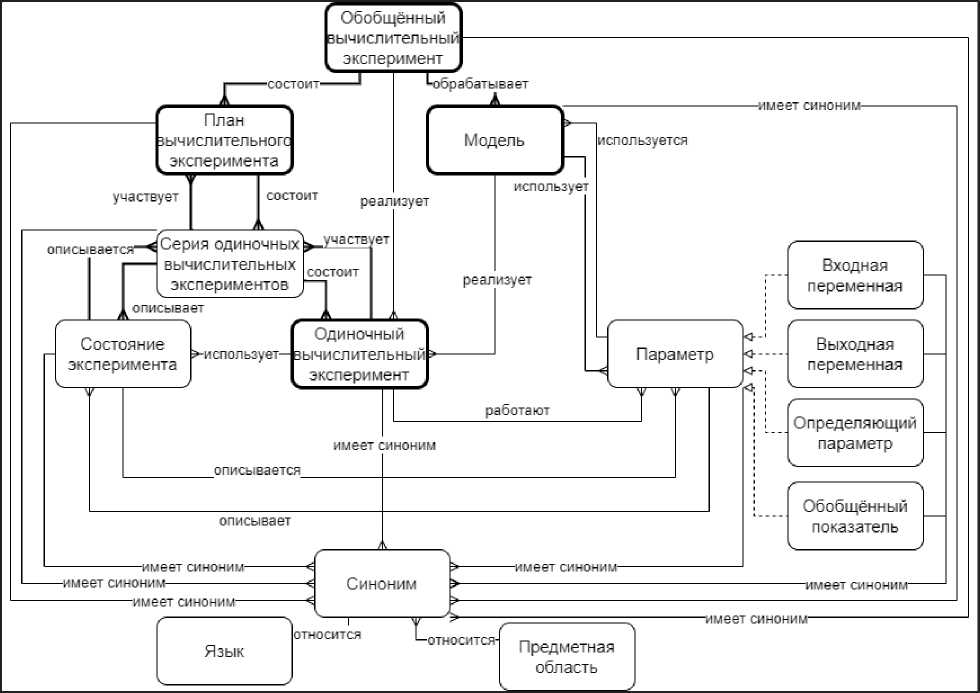
Рисунок 2 – Обобщённая онтологическая схема ОВЭ

Таблица 1 - Примеры синонимов для понятия “Обобщённый вычислительный эксперимент”

Синоним	Предметные области	Язык
Описание эксперимента	Общенаучная	Русский
Generalized computational experiment	Компьютерное моделирование	Английский
Серия экспериментов	Общенаучная	Русский
Экспериментальное исследование	Общенаучная	Русский

Предложенная обобщённая онтологическая модель ОВЭ позволяет создать дополнительный (верхний) уровень абстракции хранилища ОВЭ, с которым исследователь может взаимодействовать более эффективно по сравнению с доступом к хранилищу напрямую. Для обеспечения поддержки функционирования и взаимосвязи этого уровня с нижележащими уровнями хранилища ОВЭ разработана структура метаданных ОВЭ с учётом его онтологических особенностей (рисунок 3). Эта структура позволяет сформировать описание ПрО в привычных исследователю терминах, однозначно сопоставляемых с понятиями хранилища

ОВЭ, а также указать спецификацию параметров, показателей и переменных, используемых в ОВЭ. Дополнительно исследователь с помощью этого описания может задать метод оценки состояния ОВЭ.

Таблица 2 - Примеры синонимов для понятия “Модель”

Синоним	Предметные области	Язык
Солвер	Компьютерное моделирование	Русский
Model	Общенаучная	Английский
Функция	Математика	Русский
Алгоритм	Математика	Русский
Метод	Общенаучная	Русский
Черный ящик	Информационные технологии	Русский
Программа	Общенаучная	Русский
Мутация	Генетика	Русский
Численный метод	Математика	Русский
Вариант	Общенаучная	Русский
Версия	Общенаучная	Русский
Модификация	Общенаучная	Русский

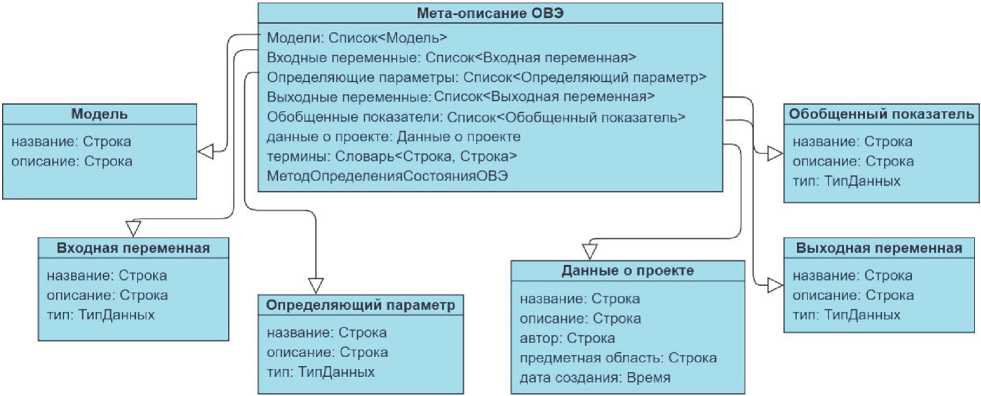
Рисунок 3 - Структура метаданных для работы с хранилищем ОВЭ

4    Апробация и обсуждение результатов

Для апробации предложенных подходов и методов использовались данные ОВЭ, проводившегося с целью верификации и оценки точности солверов (от англ. solver - решатель) платформы OpenFOAM для трёхмерной задачи сверхзвукового обтекания клина [15] (в терминологии OpenFOAM солверы представляет собой программные модули, в которых реализованы различные численные модели механики сплошных сред [16]).

Фрагмент мета-описания для данного ОВЭ представлен в следующем виде.

• 1)    Словарь терминов <« понятие из онтологии », « используемый синоним »> :

<«обобщённый вычислительный эксперимент », «обобщённый вычислительный эксперимент »>; <« модель », « солвер »>; <« план вычислительного эксперимента », « серия вычислительных экспериментов »>; <« одиночный вычислительный эксперимент », « вычислительный эксперимент »>; <«входная переменная », «входная переменная »>; <определяющий параметр », « определяющий параметр »>; <« выходная переменная », « выходная переменная »>; <« обобщённый показатель », « норма ошибки »>.

• 2)    ПрО : верификация численных методов.

• 3)    Модели : risoCentralFOAM , pisoCentralFOAM , sonicFOAM , QGDFoam .

• 4)    Входные переменные: площадь и положение ячеек дискретизации. Тип данных - вещественный.

• 5)    Выходные переменные: давление в ячейках. Тип данных - вещественный.

• 6)    Определяющие параметры: угол набегающего потока, число Маха набегающего потока. Тип данных - вещественный.

• 7)    Обобщённые показатели: норма L1, норма L2. Тип данных - вещественный.

На основе словаря терминов получена онтологическая схема хранилища ОВЭ для ПрО математического моделирования и численных методов (см. рисунок 4).

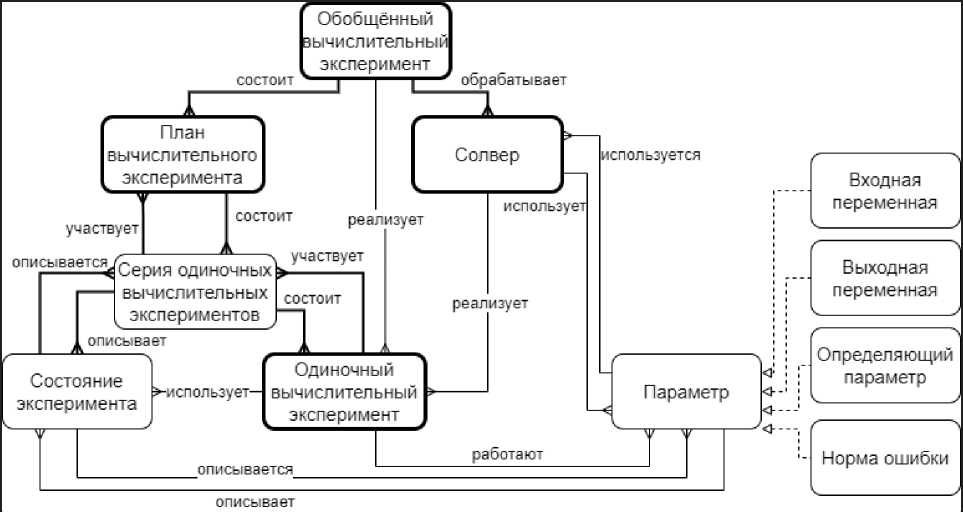
Рисунок 4 – Конкретизированная онтологическая схема ОВЭ для ПрО математического моделирования и численных методов

В хранилище были помещены сведения о 80 проведённых ВЭ. Состояние ОВЭ определялось с помощью метода, основанного на оценке точности двумерной аппроксимации при фиксированных комбинациях подмножества определяющих параметров [6]. Для этих целей с использованием имеющегося словаря терминов и мета-описания были сформированы следующие запросы к хранилищу на получение данных:

• 1)    выбрать все возможные значения определяющего параметра «угол набегающего потока».

• 2)    для всех комбинаций значений определяющего параметра «угол набегающего потока», модели и обобщённого показателя выбрать множество пар (значение «число Маха набегающего потока», значение обобщённого показателя).

• 3)    выбрать все возможные значения определяющего параметра «число Маха набегающего потока».

• 4)    для всех комбинаций значений определяющего параметра «число Маха набегающего потока», модели и обобщённого показателя выбрать множество пар (значение «угол набегающего потока», значение обобщённого показателя).

Полученные результаты выборок использовались для построения аппроксимирующих кривых, которые в дальнейшем подвергались визуальному анализу.

В ходе визуального анализа удалось обнаружить возможную неточность в данных для солвера sonicFOAM при значении числа Маха набегающего потока, равном 4, и значении угла набегающего потока, равному 20 градусам. Это привело к необходимости повторного проведения соответствующего одиночного ВЭ, в ходе которого данное предположение подтвердилось, а в хранилище ОВЭ были помещены уточнённые значения указанных определяющих параметров для данного одиночного ВЭ.

Отмеченный факт является подтверждением того, что систематическое и структурированное накопление и хранение сведений о проведённых ВЭ позволяет в дальнейшем проводить анализ всего ОВЭ, в ходе которого становится возможным как определение некорректно проведённых ВЭ, так и корректировка плана проведения ОВЭ. Осуществить подобную систематизацию без применения представленного онтологического подхода к формализации представления и обработки данных об ОВЭ было бы затруднительно. Применение тезауруса к онтологической схеме хранилища позволяет получить адаптированную версию онтологической схемы в терминах соответствующей ПрО и упростить исследователю взаимодействие с ней: представляется возможным формирование запросов на выборку данных в более привычных исследователю терминах.

Заключение

Предложен подход к построению хранилища ОВЭ, основанный на применении методов онтологического инжиниринга. Определены основные особенности хранения ОВЭ, разработана и обоснована схема построения хранилища, включающая дополнительный верхний уровень абстракции. На верхнем уровне исследователь взаимодействует с привычными ему терминами, а на нижних уровнях взаимодействие с данными осуществляется посредством традиционных подходов, реализуемых в современных СУБД.

Исследователю предоставляется возможность оперировать привычными ему понятиями, что положительно сказывается на качестве проводимых исследований с использованием разработанного хранилища ОВЭ.

Проведённые экспериментальные исследования на примере оценки точности решения задач механики сплошных сред с применением различных численных методов подтвердили работоспособность предложенного подхода, а также позволили выделить направления дальнейших исследований:

• 1)    расширение числа ПрО и соответствующего тезауруса;

• 2)    расширение онтологической модели за счёт выделения в ней типовых видов запросов данных, адаптированных к различным ПрО;

• 3)    программная реализация предложенных подходов по формированию и преобразованию запросов от исследователя на понятном ему языке к их выполнению в соответствующей СУБД;

• 4)    развитие методов и технологий визуализации данных, получаемых из разработанного хранилища ОВЭ.