Построение эпидемической модели для безмасштабной сети для защиты от вирусных атак
Автор: Чернышова Е.В., Засорин Д.С., Ерохина Т.В.
Журнал: Международный журнал гуманитарных и естественных наук @intjournal
Рубрика: Технические науки
Статья в выпуске: 1-1 (40), 2020 года.
Бесплатный доступ
В работе проводятся основные этапы построения макромодели безмасштабной сети для обеспечения информационной безопасности в ней. Безмасштабная сеть представляет собой граф, в котором степени вершин распределены по степенному закону и потому максимально отражают реальные информационно-коммуникационные сети с большим количеством узлов. Степенные функции в полной мере позволяют описать динамические свойства и вероятности меры риска заражения компьютерными вирусами, как эпидемиологическими алгоритмами. Для построения эпидемической модели определяются функции риска распространения вируса на первоначальном и последующих этапах, степень опасности вредоносного контента, число узлов подвергшихся атаке для предотвращения распространения по сети эпидемии. Моделирование безмасштабных сетей позволяет эффективно анализировать данные в социальных сетях и обеспечивать защиту от вирусных атак.
Безмасштабная сеть, модель эпидемического процесса, эпистойкость, информационная безопасность
Короткий адрес: https://sciup.org/170186711
IDR: 170186711 | DOI: 10.24411/2500-1000-2020-10044
Текст научной статьи Построение эпидемической модели для безмасштабной сети для защиты от вирусных атак
Посредством эпидемиологических алгоритмов злоумышленник имеет возможность оказывать влияние на информацию в безмасштабных сетях. Такие алгоритмы обеспечивают не только высокий уровень ущерба на уровне владельца безмасштаб-ной сети, но и простоту внедрения. Подобно тому, как зараженный человек передает вирус людям, с которыми он вступает в контакт, каждый пользователь безмас-штабной сети пересылает полученную им новую информацию друзьям или случайно выбираемым пользователям. Эти пользователи распространяют информацию другим пользователям и т.д. Для проведения практического исследования безмасштаб-ных сетей (SN) можно использовать иерархическую модель, которая позволит более эффективно провести необходимые математические операции.
Оценим риск и эпистойкость на последующем этапе распространения эпидемии, где:
n функция риска начального этапа эпидемии,
k[о] функция риска последующего этапа эпидемии, N – количества вершин графа, k – степени вершин, P(k) – степенной характеристики вершин k от количества вершин графа, kmin и kmax – степени вершины, минимальная и максимальная соответственно, M = k max-kmin – количество слоев, р5(к) – вероятность при распространении вирусной эпидемии, заражения вершины со степенью k, Ω к–коэффициент, (в диапазоне (0;1]), оценивающий степень опасности передачи на некоторую вершину вредоносного контента, ẟ – цена вершины для каждого слоя, ε(k) – коэффициент ценности узла степени k, L(k|s) – коэффициент связности узлов, G – число вершин подвергшихся вредоносному воздействию, Uк – ущерб для слоя, Ԝк – польза от защиты, I[n] – количество вершин зараженных на начальном этапе [1, 2].
kmax
Risk[о] = Risk[n] + ^ PUi [о] ; i=kmin kmax kmax
Risk[о] = ^ Ν(k|r)I [n]ẟ + РU[о]
kmjn i-kmin
О-U2 [о]
Ν[о]= ; Ν[о]
UZ [о] k∗φ к
∑ Р(k)∗Т∗ kР (k)
U[n]+∑ I [n]∑i-kmintр8( )Ν(r|i)iẟ -1
Risk[j+1] =Risk[j] +
Ν[j+1]=
2^ РUs[j+1];
S—kmjn
О-U z [j+1] Uz[j+1]
; Us[j+1]
I[n] =
^ Ω ∗Р(r)∗r∗Р(k)
-kmin
=Is [j] 2^ [р K(S|i)]ẟ i-kmjn
U
= ΩР(r)rР(k)
kmjn i-kmjn
Ω Р(i)iР(r)ẟ
Получим формулы риска и ущерба на n – шаге:
kmax kmax
Uz[j+1]= Uz[j]+ 2^ I [j] 2^ n(S|i)ẟ ; S —kmin '-kmln
Распространение эпидемии в условиях рассматриваемой безмасштабной информационно-коммуникационной сети идет каскадно вниз [2], поэтому для оценки ущерба целесообразно взять из матрицы послойной связности строку связей всех рассматриваемых в матрице вершин, с вершиной с максимальной степенью связности. В таблице 1 представлены связи вершины максимальной степени с другими вершинами.
Таблица 1. Связи вершины максимальной степени с другими вершинами
|
S |
|||||||||||||||||
|
n |
216 |
215 |
214 |
213 |
212 |
211 |
210 |
209 |
208 |
207 |
206 |
205 |
204 |
203 |
202 |
201 |
200 |
|
K |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Коэффициент оценки опасности распространения эпидемии на узел (вершину) (Ω ) определим по формуле:
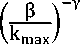
=1-(е -k )
где β – коэффициент распространения вирусной эпидемии на узел. Для заданной сети примем значение β= 0,8. В таблице 2 представлены результаты расчёта коэффициента оценки опасности распространения эпидемии на узел, вероятности заражения, ценность вершин.
Таблица 2. Результата расчёта значений Ω , р5 ( ) , ẟ .
|
k |
Ωк |
р8(к) |
ẟк I |
|
216 |
0,800 |
0,581 |
0,0137 |
|
215 |
0,805 |
0,592 |
0,0135 |
|
214 |
0,811 |
0,602 |
0,0133 |
|
213 |
0,817 |
0,613 |
0,0131 |
|
212 |
0,822 |
0,624 |
0,0129 |
|
211 |
0,828 |
0,635 |
0,0127 |
|
210 |
0,833 |
0,647 |
0,0125 |
|
209 |
0,839 |
0,658 |
0,0123 |
|
208 |
0,845 |
0,670 |
0,0121 |
|
207 |
0,850 |
0,682 |
0,0119 |
|
206 |
0,856 |
0,695 |
0,0117 |
|
205 |
0,862 |
0,708 |
0,0115 |
|
204 |
0,868 |
0,720 |
0,0113 |
|
203 |
0,873 |
0,734 |
0,0111 |
|
202 |
0,879 |
0,747 |
0,0109 |
|
201 |
0,885 |
0,761 |
0,0108 |
|
200 |
0,891 |
0,775 |
0,0106 |
Вычислим значение функции риска нулевого этапа вирусной эпидемии:
Risk[0] = 0,0137 ∗ 0,581 = 0,008
Найдем среднее количество зараженных вершин (I к [n]) на начальном этапе, ущерб Uк [n] для каждого k-слоя, количество здо- ровых (незаражённых) вершин S к [n] на k-слоях. В таблице 3 представлены результаты расчёта количества заражённых вершин на начальном этапе распространения вирусной эпидемии.
Таблица 3. Расчёт количества заражённых и незараженных вершин на первом шаге
|
k |
216 |
215 |
214 |
213 |
212 |
211 |
210 |
209 |
208 |
207 |
206 |
205 |
204 |
203 |
202 |
201 |
200 |
|
Iк [n] |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Uк [n] |
0,91 |
0,89 |
0,87 |
0,85 |
0,83 |
0,81 |
0,79 |
0,78 |
0,76 |
0,74 |
0,72 |
0,70 |
0,68 |
0,66 |
0,64 |
0,62 |
0,61 |
|
1 |
1 |
0 |
1 |
2 |
9 |
9 |
2 |
1 |
0 |
2 |
4 |
4 |
6 |
8 |
9 |
1 |
|
|
S к [n] |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
Исходя из этого, найдем пользу от защиты ωк [n] и эпистойкость Q к[n]. В таблице 4 представлена польза от защиты на первом шаге атаки.
Таблица 4. Польза от защиты на первом шаге атаки
|
k |
21 6 |
21 5 |
21 4 |
21 3 |
21 2 |
21 1 |
210 |
209 |
208 |
207 |
206 |
205 |
204 |
203 |
202 |
201 |
200 |
|
ωк [n] |
0 |
0 |
0 |
0 |
0 |
0 |
0,74 7 |
0,76 0 |
0,78 2 |
0,79 6 |
0,80 4 |
0,82 4 |
0,83 3 |
0,84 2 |
0,85 9 |
0,97 0 |
0,98 7 |
|
Q к [n] |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
Risk[n]на начальном этапе эпидемии: kpnax
Risk[n] = Ν(k|r)Iг[n]ẟг r=kmin соответственно: Risk[n] =0,47813.
Так как уже на втором этапе распространения вирусной эпидемии, согласно матрицы внутрисетевой связанности все вершины подвержены атаке [3], то считаем второй этап распространения демии.
Ущерб на втором этапе вирусной демии:
про-эпи-
эпи-
Uг [о] =
∑ r=kmin αгР(r)rР(k) ∑ hmin αiР(i)iР(r)ẟi ,U r [о] = 0,875024
Риск на втором этапе вирусной эпидемии:
Risk[о] = ∑ r=kmi Ν(k|r)Ir[n]ẟr+
∑ i=km РU i [о] , Risk[о] = 0,375176
Эпистойкость на последующем этапе атаки может быть рассчитана:
Т[о] = к∗Фк
∑Lk P(к)∗T∗ kmax
∑ ( )∗ ∗ ( )
[] ∑ []∑ () (|)
1 , Ν[о] =0,613281
Реализация атак по эпидемиологическим алгоритмам, может грозить не только колоссальными финансовыми потерями для владельца сети, но и огромным ущербом. В связи с этим важнейшей задачей является обеспечение эпистойкости сетей на необходимом уровне для их эффективного функционирования и, в конечном счёте, минимизации ущерба от деструктивных деяний. Изучение таких атак в сетях социальных закладок и методов противодействия им – крайне актуальная задача. Она является сложной и многогранной, так как требует исследования множества факторов, ключевым из которых является риск-анализ. В безмасштабных сетях показатель степени зараженности при произвольном удалении узлов и их критического числа, которое измеряется отношением числа удалённых узлов к общему числу узлов в сети, распадается на отдельные фрагменты [4, 5]. Следовательно, такие безмасштабные сети очень устойчивы к внешним воздействиям. Но, у таких сетей существует своя уязвимость, такая как целенаправленное повреждение одного или нескольких узлов с большим числом связей ведёт к дезинтеграции сети. Проблема устойчивости сети связано задача распространение инфекции. Низкая скорость распространения инфекции объясня- ется высокой долей удалённых узлов сети. Актуальность данной работы подтверждается отсутствием параметров сопротивления вирусным эпидемиям в сети.
Следует подчеркнуть аналитический характер полученных результатов, что открывает перспективу численных многовариантных расчётов и оптимизации в целях управления эпистойкостью системы.
Список литературы Построение эпидемической модели для безмасштабной сети для защиты от вирусных атак
- Построение дискретной макро-модели для безмасштабной сети / Скрыпников А.В., Чернышова Е.В., Прокофьев О.Е. // Материалы II международной научно-практической конференции "Инновационные подходы и современная наука". - Киев: Центр научных публикаций, 2016. - С. 128-132.
- Нормирование требований к характеристикам программных систем защиты информации / Скрыпников А.В., Хвостов В.А., Чернышова Е.В., Самцов В.В., Абасов М.А. // Вестник Воронежского государственного университета инженерных технологий. - 2018. - Т. 80. № 4 (78). - С. 96-110.
- Обоснование закономерностей и расчёт параметров для распределения степени вершин безмасштабной сети / Скрыпников А.В., Чернышова Е.В., Прокофьев О.Е. // Материалы международной научно-практической конференции "Вопросы образования и науки". - Научный альманах. № 5-3 (19). - Тамбов, 31 мая 2016 г. - С. 156-160.
- Риск-модели процесса реализации целенаправленных атак с использованием технологий ROOTKIT / Чернышова Е.В., Колпакова Т.А., Каширо П.А., Золотухина У.В. // В сборнике: стандартизация, управление качеством и обеспечение информационной безопасности в перерабатывающих отраслях АПК и машиностроении. - 2016. - С. 404-409.
- Эталонное моделирование критически важных объектов информатизации при комплексном обеспечении их информационной безопасности / Дубровин А.С., Лютова Т.В., Чернышова Е.В. // В сборнике: Современные инструментальные системы, информационные технологии и инновации, сборник научных трудов XII-ой Международной научно-практической конференции: в 4-х томах. Ответственный редактор: Горохов А.А. - 2015. - С. 64-68.


