Построение калибровочной линии при фрагментном анализе ДНК

Фрагментный анализ является одним из основных научных методов определения видовой принадлежности, выяснения степени родства различных групп организмов, идентификации сортов растений и пород животных, а также для обнаружения отрицательного и полезного признака организма. Знание длины фрагментов ДНК необходимо при установлении отцовства или других родственных взаимоотношений. Этот анализ основан на сравнении фрагментов ДНК между предполагаемым отцом (матерью) и данным ребенком [1].

При определении длины анализируемых фрагментов их сигналы получаются в 4 каналах флуоресцентного детектора, а в 5-м канале регистрируются сигналы внутреннего стандарта (маркера длины) фрагментов ДНК. Внутренний стандарт М 450, или S 450, содержит 24 фрагмента длиной от 60 до 450 нуклеотидов [2]. Этот калибратор имеет наименьшую цену и применяется чаще других. Следующий внутренний стандарт 600 LIZ содержит 36 фрагментов длиной от 20 до 600 нуклеотидов [3]. Мы работали с 600 LIZ.

Во время разделения фрагментов ДНК в капилляре под действием электрического поля на выходе пятиканального детектора регистрируются 5 цифровых последовательностей пиков [4]. При этом каждому цифровому отсчету соответствует точка графика, имеющая по горизонтальной оси (оси времени) номер отсчета, а по вертикальной оси — значение интенсивности флуоресценции в относительных единицах (о. е.).

Обычно обработка сигналов начинается с устранения начального смещения и дрейфа уровня базовой линии отдельно в каждом цветовом канале [5]. После небольшой фильтрации шумов определяются положения пиков в каждом спектральном канале [6, 7].

В настоящей статье предложен способ оптимальной аппроксимации сигналов внутреннего стандарта фрагментов ДНК с целью уменьшения погрешностей при определении длины фрагментов ДНК.

ОБРАБОТКА СИГНАЛОВ ФЛУОРЕСЦЕНТНОГО ДЕТЕКТОРА

График сигналов флуоресценции внутреннего стандарта 600 LIZ приведен на рис. 1. В результате определения положения центров пиков заполняются ячейки электронной таблицы, отражающие дискретную зависимость номеров пиков от времени. Для обеспечения калибровки предлагается следующая последовательность действий на электронной таблице при обработке сигналов калибровочной смеси:

– задание ограничительных параметров калибровочных пиков;

– ручное присвоение в таблице каждому калибровочному пику соответствующей известной длины (при необходимости удаление лишних пиков);

– аппроксимация дискретных сигналов непрерывной функцией;

– определение длины анализируемых фрагментов;

– автоматическое или полуавтоматическое присвоение в таблице каждому калибровочному пику соответствующей известной длины при последующих анализах.

В качестве ограничительных параметров можно использовать минимальную высоту и минимальную ширину пиков, а также временной интервал (начало и конец) выхода пиков.

Задание минимальной высоты и ширины пиков устраняет многие пики, не принадлежащие калибровочной смеси ("лишние" пики).

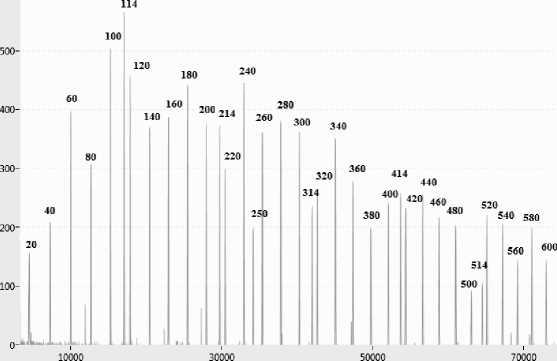
Рис. 1. График сигналов флуоресценции калибратора 600 LIZ.

Горизонтальная ось — номер отсчета, вертикальная ось — значение интенсивности флуоресценции в относительных единицах (о. е.)

Задание начала и конца временнóго интервала приводит к автоматическому определению первого и последнего пиков калибровочной последовательности.

В результате ручного присвоения каждому калибровочному пику соответствующей известной длины получается таблица пиков, содержащая дискретную экспериментальную ("сырую") зависимость длины фрагментов от положения на оси времени. Для определения длины произвольных анализируемых фрагментов необходимо аналитически описать зависимость длины калибровочных фрагментов от времени в виде непрерывной функции. Наиболее простыми способами получения непрерывной функции могут быть кусочнолинейная интерполяция (ломаная линия) и сплайн. Эти способы обладают следующими недостатками:

– к погрешности определения положения анали- зируемых пиков добавляется погрешность определения калибровочных пиков, поскольку все значения таблицы принадлежат непрерывной функции;

– эти непрерывные функции не позволяют сделать правильный прогноз продолжения калибровки за пределами калибровочных пиков.

Предлагается использовать аналитическую функцию, наиболее соответствующую физическому процессу электрофореза фрагментов ДНК в геле, а именно полиномиальную аппроксимацию. Далее показано, что аппроксимация табличной функции степенным полиномом позволит оптимально усреднить погрешности определения положения калибровочных пиков, построить график калибровочной линии, а также успешно использовать степенной полином за пределами калибровочных пиков.

Табл. 1. Результаты вычисления аппроксимирующей функции, полученные с помощью метода последовательного приближения (образ электронной таблицы)

A	B	C	D	E	F	G	H	I	J	K
1	4480	20	2530.06	5132	652	1018559	-12.4	20.41	0.41	37.7
2	7280	40	130.36	7722	442		0.00728	41.12	1.12
3	9992	60	-0.01	10302	310		9.70E-09	61.34	1.34
4	12656	80	-1.25E-07	12870	214		2.50E-14	81.36	1.36
5	15304	100	-2.00E-08	15426	122		6.10E-19	101.41	1.41
6	17080	114		17209	129			114.95	0.95
⁞
36	72928	600		73173	245			597.06	2.94

АППРОКСИМАЦИЯ СИГНАЛОВ КАЛИБРОВОЧНОЙ СМЕСИ

Численное сравнение погрешностей аппроксимации табличной функции степенными полиномами 4-й и 3-й степеней выполнены в среде Excel [8]. В столбцах А , В и С табл. 1 приведены соответственно порядковые номера калибровочных пиков, положения на оси времени (отсчеты) и соответствующие длины фрагментов (в единицах нуклеиновых кислот, сокращенно "н. к."). Эта исходная табличная функция получена при ручном присвоении известной длины каждому калибровочному пику. Ее график можно представить в виде: y = = f ( x ), или в обозначениях табл. 1: С = f ( B ).

Далее рассмотрено 2 варианта аппроксимирующей функции. При первом варианте значения в столбце С (длины фрагментов) остаются постоянными, а изменяются значения положения пиков на оси времени. При втором варианте значения в столбце В остаются постоянными, а изменяются длины фрагментов.

Для реализации первого варианта аппроксимирующая функция выражена в виде полинома 4-й степени в столбце E :

E1=$D$1+$D$2*C1+$D$3*C1^2+ +$D$4*C1^3+$D$5*C1^4.

В столбце F вычислена погрешность определения исходного положения пиков: F1=Е1-В1.

В столбце G вычислена сумма квадратов погрешностей из столбца F .

Величины $D$1–$D$5 выбраны из условия максимального совпадения графиков функций С = = f (B) и С = f (Е), а затем уточнены с помощью метода наименьших квадратов (минимум величины G1) и метода последовательного приближения в меню "Данные\Анализ\Поиск решения" [2].

Уточненное графическое изображение функции С = f ( Е ) можно принять в качестве графика калибровочной линии. Если на этом графике выделить точки, соответствующие С1 , С2 и т. д., то заметны отклонения горизонтальных координат этих точек от экспериментально определенных центров пиков В1 , В2 и т. д., связанные с погрешностью измерения координат пиков.

Второй вариант аппроксимирующей функции выражен полиномом 4-й степени в столбце I :

I1=$H$1+$H$2*B1+$H$3*B1^2+ +$H$4*B1^3+$H$5*B1^4 .

В столбце J вычислены погрешности определения длин фрагментов соответствующих пиков: J1= I1–С1 .

В столбце K вычислена сумма квадратов погрешностей из столбца J . Величины $Н$1–$Н$5 выбраны и уточнены по методу наименьших квадратов (минимум величины в ячейке К1 ) по методике, использованной в предыдущей формуле.

Ценность второго варианта аппроксимирующей функции заключается в том, что при ее вычислении явно определены погрешности экспериментального определения центров пиков (в столбце J ). Равномерность распределения и величина этих погрешностей характеризует качество аппроксимации.

Лучшее качество аппроксимации может быть достигнуто путем использования функций Excel, осуществляющих операции с матрицами. Для этого на 2-м листе кроме прежних столбцов А , В и С формировалась матрица, столбцы которой E , F , G , H , I содержали значения B^0 , B^1 , B^2 , B^3 и B^4 .

Табл. 2. Результаты вычисления аппроксимирующей функции, полученные путем использования функций Excel, осуществляющих операции с матрицами (образ электронной таблицы)

А	H	I	J	K	L	M	N	O
1	-10.5865	20.05	0.05	1.31	-16.4138	18.04	-1.96	25.13
2	6.6255E-03	40.05	0.05		0.00771	39.53	-0.47
3	5.1501E-08	59.94	-0.06		-4.9E-09	60.33	0.33
4	-8.8835E-13	79.89	-0.11		2.02E-13	80.78	0.78
5	6.9947E-18	100.07	0.07			101.15	1.15
6		113.77	-0.23			114.84	0.84
⁞
36		599.80	-0.20			597.96	-2.04

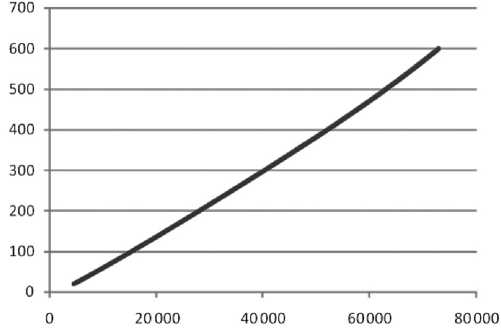
Рис. 2. График калибровочной линии 600 LIZ.

Обозначения осей аналогичны рис. 1

Выделялась область К11:О15 с обозначением операции FT*F . В строку ввода записывался символ операции

=МУМНОЖ(ТРАНСП(E1:I36),E1:I36), комбинацией клавиш Ctrl+Shift+Enter результат этой и последующих операций вставлялся в выделенную область.

Выделялась область К19:О23 с обозначением (FT*F)–1 . В строку ввода записывался символ операции

=МОБР(K11:O15) .

Выделялась область К27:К31 с обозначением FT*y . В строку ввода записывался символ операции

=МУМНОЖ(ТРАНСП(E1:I36),B1:B36) .

Выделялась область К27:К31 с обозначением H=(FT*F)-1*(FT*y) . В строку ввода записывался символ операции

=МУМНОЖ(K19:O23,K27:K31).

В столбец Н табл. 2 внесены коэффициенты аппроксимирующей функции с полиномом четвертой степени, полученные в результате последней операции. По этим коэффициентам построена аппроксимирующая функция в столбце I . Погрешность определения центров пиков приведена в столбце J , максимальная погрешность — не более 0.5 н. к. Видно, что сумма квадратов в ячейке К1 табл. 2 значительно меньше, чем аналогичная величина в ячейке К1 табл. 1, полученная методом последовательного приближения.

В столбец L табл. 2 внесены коэффициенты аппроксимирующей функции с полиномом 3-й сте- пени. Максимальная погрешность в столбце М — более 2 н. к. При этом сумма квадратов в ячейке O1 табл. 2 многократно превосходит ту же величину в ячейке K1.

ВОЗМОЖНОСТЬ ЭКСТРАПОЛЯЦИИ АППРОКСИМИРУЮЩЕЙ ФУНКЦИИ

ЗА ПРЕДЕЛЫ КАЛИБРОВОЧНЫХ ПИКОВ

Предлагается аппроксимирующую функцию калибратора 600 LIZ построить в пределах 500 нуклеотидов. В этом случае оставшийся интервал 100 нуклеотидов (6 пиков) можно использовать для определения погрешностей экстраполяции.

В столбец Н табл. 3 внесены коэффициенты аппроксимирующей функции полинома 4-й степени при калибровке в пределах 500 нуклеотидов,

По этим коэффициентам построена аппроксимирующая функция в столбце I. Погрешность определения центров пиков приведена в столбце J , максимальная погрешность — не более 0.5 н. к. Поэтому график табличной функции (столбец С табл. 1) и график калибровочной линии (столбец I табл. 3) на рис. 2 практически совпадают.

В ячейке К1 табл. 3 вычислена сумма квадратов по 30 пикам. В ячейке К2 табл. 3 вычислена сумма квадратов по всем 36 пикам. Видно, что сумма квадратов в ячейке К2 табл. 3 незначительно отличается от аналогичной величины в ячейке К1 табл. 2. Этот результат подтверждает возможность экстраполяции аппроксимирующей функции за пределы калибровочных пиков.

Аналогичные построения и вычисления выполнены для случая, когда в столбец L табл. 3 внесены коэффициенты аппроксимирующей функции с полиномом 3-й степени при калибровке в пределах 500 нуклеотидов. Максимальная погрешность определения 36-го пика за пределами калибровки составляет — 8.87 н. к., сумма квадратов по всем 36 пикам — 164.97 н. к. Эти результаты значительно хуже, чем результаты при аппроксимирующей функции с полиномом 4-й степени.

ЗАКЛЮЧЕНИЕ

Предложена последовательность действий при обработке сигналов внутреннего стандарта длины фрагментов ДНК.

Предложено использовать полиномиальную аппроксимацию в качестве аналитической функции, наиболее соответствующей физическому процессу электрофореза фрагментов ДНК в геле.

Выполнено численное сравнение параметров аппроксимирующих функций, полученных в Excel

Табл. 3. Результаты вычисления аппроксимирующей функции при калибровке в пределах 500 нуклеотидов (образ электронной таблицы)

А H I J K L M N O 1 -10.5726 20.06 0.05 1.04 -14.034 19.05 -0.95 7.13 2 0.0066 40.05 0.05 1.34 0.007345 39.92 -0.08 164.97 3 5.16E-08 59.94 -0.06 8.84E-09 60.29 0.29 4 -8.9E-13 79.89 -0.11 5.8E-14 80.46 0.46 5 7E-18 100.07 0.07 101.15 1.15 ⁞ 31 513.62 -0.38 512.01 -1.99 32 519.99 -0.01 518.06 -1.94 33 539.98 -0.02 536.84 -3.16 34 559.90 -0.10 555.26 -4.74 35 580.26 0.26 573.76 -6.24 36 599.72 -0.28 591.13 -8.87 с помощью метода последовательного приближения и путем использования функций, осуществляющих операции с матрицами.

Выполнено численное сравнение погрешностей аппроксимации табличной функции степенными полиномами 3-й и 4-й степеней. Показано, что степенной полином 4-й степени при аппроксимация табличной функции позволяет оптимально усреднить погрешности определения положения калибровочных пиков до величины 0.5 н. к., построить график калибровочной линии, а также успешно использовать его за пределами калибровочных пиков еще на 100 н. к.

Работа выполнена при поддержке Министерства образования и науки Российской Федерации в рамках Федеральной целевой программы "Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007– 2013 годы" и опытно-конструкторской работы "Разработка генетического анализатора для секвенирования и фрагментного анализа ДНК" (шифр заявки "20112,2-522-014-001",       Государственный контракт

№ 16,522,12,2014 от 10 октября 2011 г.).