Построение математической модели производительности бункерного загрузочно-ориентирующего устройства с наклонным диском и тангенциальными карманами для цилиндрических заготовок с фланцем

Для автоматической загрузки цилиндрических и сложной формы ступенчатых заготовок было предложено регулируемое механическое дисковое бункерное загрузочно-ориентирующее устройство (БЗУ) с наклонным диском и тангенциальными карманами и разработаны конструктивные ограничения на органы захвата и ориентирования заготовок в нем [1, 2]. На ранних стадиях проектирования БЗУ необходимо разрабатывать математические модели вероятности захвата и производительности, что позволит оценить производительность устройства и принять меры по ее увеличению и выбрать параметры БЗУ, на которых достигаются требуемые значения производительности [3-5].

В основе построения математических моделей вероятности захвата заготовок тел вращения в механических дисковых бункерных загрузочно-ориентирующих устройствах (БЗУ) лежит представленная в работах [6, 7] концепция, в которой заложены основы теории вероятностей, что позволяет описать принципы захвата единичной заготовки из общей массы. Основываясь на данной концепции для описания влияния на производительность БЗУ его конструктивных и кинематических параметров, геометрических параметров заготовок, коэффициентов трения между ними, была разработана мате- матическая модель вероятности захвата стержневых ступенчатых цилиндрических заготовок в механическом дисковом БЗУ с наклонным вращающимся диском и тангенциально расположенными по его периферии карманами [8, 9].

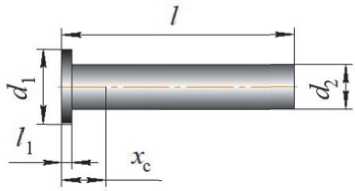
Рис. 1. Стержневая заготовка с фланцем и ее основные параметры

В данной статье предлагается разработанная математическая модель вероятности захвата и производительности для стержневых заготовок с фланцем (рис. 1) в механическом дисковом БЗУ с тангенциальными карманами.

Математическая модель БЗУ с тангенциальными карманами для заготовки с фланцем будет построена на основе представленной в работе [10] концепции.

ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ВЕРОЯТНОСТИ ЗАХВАТА

Математическая модель вероятности захвата представляет собой произведение вероятностей

η= p_ip_c

Г ^

1    4----

1) к   ^и пред )

где p_i , p_c – вероятности, характеризующие соответственно благоприятное положение заготовки для ее захвата и отсутствие помех от сцепляемости заготовок; и _пр_ед - предельное значение окружной скорости и , при которой заготовка в карман не успеет запасть [10].

Вероятности p_i и p_c определяются по полученным выражениям:

1 -

2 p _б + 0,5 1

-

xc

+ 0,25 d 1

Г

+ 0,5 1

-

l - x_c

- x_c )² + 0,25 d 2

1 3

2 п

×

P i = ^{1 -}1 ^{1 -}

×

×

1 - Р б

π

л - arccos

- arccos

arcsin

k

xc

+ 0,25 d⁴

- arccos

l - x_c

? X

-

x c ^l1

+ arccos

- x_c )² + 0,25 d ⁴

x c ^l1

μ

- 2arcsin — ^а д

d 1 + A

7 0,25( d ₁ + d ₂)² + 1 ²

l

- arccos ,               =

70,25( d ₁ + d ₂)² + 1 ² _?

ⁿ R ^ф захв 180 1

,

p₆ = 1 - 0,5

-

1 - cos arccos

xc x^ + 0,25 d4

-

0,5

_________ ^xc ^l1 _________ 7( x_c - 1 ₁)² + 0,25 d⁴

k

-

^ l ^xc

J ( l - x _c )² + 0,25 d 24 _?

-

x - l

- arccos , ^{c 1}      =

7( x_c - 1 ₁)² + 0,25 d⁴

arctan( ц₀ )                21 • 3 d ² + 2 d ² +

Pc = 1--/=---------------

²5y/2ⁿ 2 , _nz7 j                  + 10 d]l] + 10 d ₂( l — l )

— ^[ di + 2 dili + 2 d 2 ⁽ I ^- l 1 ^{)] L 11      2V   17J}

, где Цо - коэффициент трения между поверхностями заготовок; ад - угол наклона диска БЗУ; R - радиус вращающегося диска БЗУ по оси расположения тангенциальных карманов; фзахв - зона расположения карманов, в которой может разместиться k заготовок.

Оценим влияние геометрических параметров заготовок на вероятность захвата П на основе вероятностей P i и р _с .

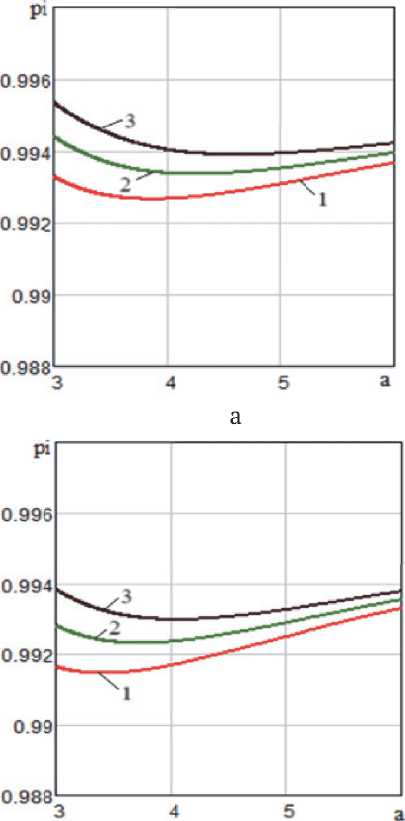
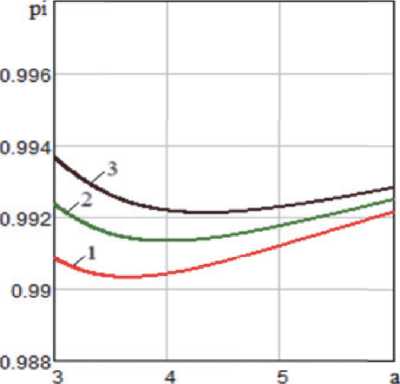
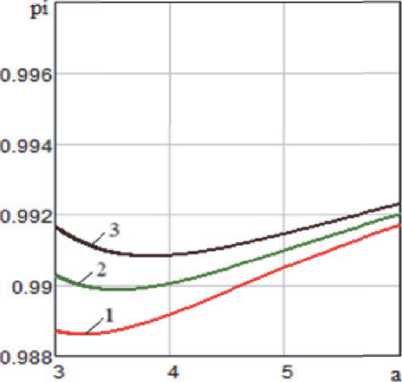
На рис. 2 представлены графики зависимостей вероятности p_i для заготовок с диаметрами d 2 = 0,5 d 1 и d 2 = 0,6 d 1 при d 1 = 0,01 м в зависимости от параметра a = l^ , угла наклона вращающегося диска а _д = 45 ° , его радиуса 0,25 м, при зазорах А = 0,1 d 1 , А = 0,2 d 1 и А = 0,3 d ^ а также коэффициентах трения ц = 0,3 и ц = 0,4 .

На вероятность pi в диапазоне а от 3 до 4,5 решающую роль оказывает величина зазора А и коэффициент трения ц , но при дальнейшем увеличении а влияние указанных параметров не на- столько существенно.