Построение механической модели элементов гетерогенной среды на основе численно-цифрового алгоритма обработки данных компьютерной томографии

В настоящее время наиболее перспективным направлением в моделировании поведения гетерогенных сред является использование данных компьютерной томографии [15, 16]. Этот подход позволяет получать информацию о структуре сложных анизотропных, мелкозернистых или пористых материалов, а также иных тел, характеризующихся неоднородностью. Эта задача особенно актуальна в ортопедической клинической практике. Так, дефекты костной ткани, связанные с всевозможными патологиями, могут оказать большое влияние на качество проводимого лечения, потому на этапе диагностики необходимо получить максимально возможную информацию о прочности и жесткости костной ткани [6, 12, 18, 20, 21].

Герасимов Олег Владимирович, лаборант-исследователь кафедры теоретической механики, Казань Бережной Дмитрий Валерьевич, к.ф.-м.н., доцент, доцент кафедры теоретической механики, Казань Большаков Павел Владиславович, лаборант-исследователь кафедры теоретической механики, Казань Стаценко Евгений Олегович, младший научный сотрудник научно-исследовательской лаборатории, Казань

Саченков Оскар Александрович, к.ф.-м.н., научный сотрудник кафедры теоретической механики, Казань

Существует несколько подходов к построению моделей элементов пористых сред, деформирующихся под действием внешних нагрузок. В первую очередь к ним можно отнести аппроксимацию распределения неоднородности методом средних пересечений линий [1, 2, 10]: в этом случае формулируются соотношения, связывающие компоненты тензора упругих констант и тензора структуры [1, 2, 7, 9, 10], характеризующего осреднённое направление пор. Другой подход – сведение анизотропии материала к ортотропии путём определения констант из численных экспериментов [5, 8, 13, 14, 17, 22, 23, 24]. В данной работе предлагается подход, основанный на учёте особенностей структуры пористого материала, выявленных по данным компьютерной томографии при построении численной модели.

Проведение компьютерной томографии элемента пористой среды предполагает создание его цифрового прототипа, представляющего собой трехмерный целочисленный массив определенной структуры [15, 16]. Элементами этого массива являются единицы или нули, которые характеризуют наличие или отсутствие вещества в определенном микроэлементе объема и отражают рентгеновскую плотность согласно шкале Хаунсфилда. Таким образом, цифровой прототип представляет структуру элемента пористой среды в виде совокупности элементарных микрообъемов (кубиков), про каждый из которых известно – содержит он вещество (кости) или нет. По этим данным на основе какого-либо приближенного метода можно построить дискретную механическую модель элемента пористой среды. Наиболее удобным с алгоритмической точки зрения в этом случае методом дискретизации (а в дальнейшем и расчета) будет метод конечных элементов.

Наивысшая точность расчета будет достигнута в случае моделирования каждого микрообъема трехмерным конечным элементом сплошной среды [15, 25, 26, 27]. Но в этом случае затраты ресурсов ЭВМ на создание дискретной модели, постпроцессорную обработку результатов и на этапе процессорных вычислений превысят все разумные пределы. Поэтому представляется целесообразным увеличить размеры конечных элементов, а каждый определенный в цифровом прототипе микрообъем считать окрестностью точки интегрирования при численном вычислении матрицы жесткости конечного элемента [19, 28]. Остается неясным вопрос определения числа квадратур в каждом из направлений при интегрировании локальной матрицы жесткости. Если число точек интегрирования по каждой координате мало, то точность решения задач на основе такого элемента может быть невысокой, так как в самом простом случае при интегрировании придется применять метод прямоугольников. Однако использование конечных элементов с очень большим числом квадратур хоть и повышает точность интегрирования в пределах элемента, но может увеличить жесткость расчетной области из-за возможно малого количества элементов.

Поэтому целью работы представляется реализация методики статического расчета элементов трехмерных пористых объектов на основе трехмерного изопараметрического линейного конечного элемента сплошной среды, построенного на основе выявленного по данным компьютерной томографии исследуемой области ее цифрового прототипа.

Материалы и методы

Создание цифрового прототипа

Для некоторого элемента расчетной области с помощью методов компьютерной томографии определяется соответствующий ему набор данных, представляющих собой трехмерную структуру. Интенсивность окрашивания микрообъемов структуры, слагающих расчетную область, отражает их рентгеновскую плотность согласно шкале Хаунсфилда. Процесс создания цифрового прототипа исследуемого объекта предполагает его разделение на большое число виртуальных микрокубиков (вокселей) размером Ax х Aу х Az с координатами центра векселя xk, yk, zk, где линейные размеры

A x , А у и A z обычно бывают равны друг другу и определяются разрешающей способностью компьютерного томографа.

Значения данных компьютерной томографии, соответствующие вокселю, бинаризируются по заданному порогу, определяемому, например, методом Отсу, отделяя плотную костную структуру от вещества в порах: если значение компьютерной томографии в текущем вокселе больше порогового значения, то этот воксель характеризует костную ткань, в противном случае – пору (рис. 1).

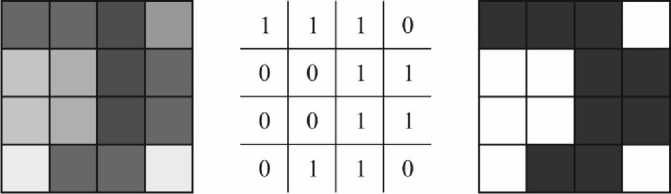
Рис. 1. Значения данных компьютерной томографии после бинаризации для одного слоя в локальной области

Численное интегрирование матрицы жесткости с учетом данных компьютерной томографии

Рассмотрим методику построения конечного элемента пористой сплошной среды на основе широко известной методики [3, 4, 11, 29] построения восьмиузлового трехмерного изопараметрического конечного элемента сплошной среды с линейной аппроксимацией геометрии и поля перемещений в локальных координатах. В рамках изопараметрической концепции для аппроксимации геометрии (радиуса-вектора точки { r } ) и исходных перемещений (вектора перемещений точки 0) используется одинаковая система функций:

f x

r = { r } = <  у 1 = ^

z

n = 1

x n

У п r N n (ZM) ,

z n

(°H

u

v

w

^ = y ^

n = 1

5 v Г

I - . j

Nn (ZM ),

где N n ( ZM ) = ¹ ( i + Z n Z ) ( i + n n n ) ( i + Z n Z )

известные линейные функции формы,

ξn , ηn , ζn – локальные координаты узлов элемента, u,v,w – проекции вектора перемещений на орты глобальной декартовой системы координат x,y,z . Соотношения (2) могут быть переписаны в матричной форме

{°}=[ N ]{0'}.

где [ N ] - матрица аппроксимирующих функций, { 0 e } - вектор узловых перемещений.

Деформацию среды описывают компоненты линейных деформаций εxx,εyy,εzz и деформации сдвига γxy,γyz ,γzx , которые представляются в виде приведенного вектора {е} и выражаются через перемещения (2) известными соотношениями Коши д и      д v     9w      ди  д v      dv  dw     ди  дw е„ = —, е = —, а = —, yxv =--+--, Yvz =--+--, Y zx =--+, xx             yy             zz             xy                     yzzx дx      ду      дz      ду  дx      дz  ду      дz

которые, в свою очередь, также могут быть записаны в матричной форме

И=[ L ]{е).

Напряженное состояние представляет тензор напряжений Коши в виде компонент нормальных σ _xx , σ _yy , σ _zz и касательных τ _xy , τ _yz , τ _zx напряжений, который, как и тензор малых деформаций, можно записать в форме приведенного вектора { о } . Закон Гука, связывающий приведенные векторы напряжений и деформаций, представляется в форме

{°}=[ D ( Г Д{8} ,

где [ D ( г ) ] - матрица упругих постоянных кусочно-однородного тела, которую можно представить в виде [5]

	"X + 2р	λ	λ	0	0	0"
	λ	X + 2р	λ	0	0	0
	X	λ	X + 2р	0	0	0
[ D ( r ) ] = [ D ] • Ю( г) =	0	0	0	μ	0	0	• ю( Г )
	0	0	0	0	μ	0
	_    0	0	0	0	0	Р _

Здесь [ D ] - тензор упругости для изотропного материала, X и р - постоянные

Ламе, определяемые через модуль упругости Юнга E и коэффициент Пуассона υ в виде

E        2μυ

р = —;----г, X =-----;

2 ( 1 + и )       1 - 2и

w( Г) - некая весовая функция, определяемая точкой в пространстве по данным компьютерной томографии.

Для вычисления матрицы жесткости конечного элемента используются известные соотношения [4, 29] вида

[ K MJK ^В ( ^г ) ] T [ D ( ^Г ) ][ B ( ^Г ) ] ^dV ,                   (9)

V где [В (r)] - матрица, связывающая приведенный вектор малых деформаций и вектор узловых перемещений [3, 4, 29]:

{ = } =[ ^В ( ^Г ) ] { 6 ■ } .

При переходе к локальным координатам соотношение (9) можно переписать в виде

[ K ] = 11 1 [ B ( 5, П, Z ) ] T [ D ( 5, n, Z ) ][ B ( 5, n, Z ) ]

- 1 - 1 - 1

x| J ( 5, n, Z)| ®(5, n, Z) d 5 d n d Z.

где | J ( 5,n,Z)| — детерминант матрицы Якоби преобразования координат.

В отличие от построения локальной матрицы жесткости изотропной сплошной среды, когда для вычисления интеграла (11) используется метод Гаусса, для пористых сред приходится использовать метод центральных прямоугольников. Конечный элемент пористой сплошной среды, как и в случае изотропии, представляет собой выпуклый шестигранник с линейчатыми четырехузловыми боковыми поверхностями. Квадратурными точками в таком элементе являются координаты центров вокселей из цифрового прототипа модели, только их, как и размеры вокселей, необходимо пересчитать в локальных координатах для каждого элемента. Тогда

[ K ' ] = L Li. CT ( 5„n , ,Z k ) [ B ( Г ( ^vw)) ] ^T x i = 1 j = 1 k = 1                        ^{L                          J}

x[ D ][ B (r (5,.nj.Z k))] IJ (5,, n, ,Z.) Д?Дл AZ, где 5i ,4, ,Zk — локальные координаты точек интегрирования; A5, An, AZ - величина шага в трёх направлениях в локальных координатах; CT(5i,nj ,Zk ) — веса квадратурной формулы, определяемые значением данных компьютерной томографии в точке интегрирования; I ,J ,K – число квадратурных точек по каждой локальной координате в элементе.

В ходе работы была реализована программа на языке программирования С++ для расчётов с использованием восьми узлового конечного элемента с тремя степенями свободы в каждом узле: перемещения вдоль соответствующих декартовых координатных осей. Решение задач осуществлялось на компьютере следующей комплектации: процессор – AMD Ryzen 7 1700 с 8 физическими и 16 логическими ядрами с частотой 3,7 ГГц, оперативная память – G.Skill Aegis 16 GB DDR 4 16 GISB K 2 3000 C 16 с частотой 2933 МГц, материнская плата – MSI B 350 M MORTAR . Ввиду больших трудозатрат при интегрировании локальной матрицы жесткости в программе было реализовано распараллеливание алгоритма с использованием технологии OpenMP , в рамках которого расчет локальной матрицы жесткости для каждого конечного элемента производился на разных потоках. Полученные результаты визуализировались в программе ParaView .

Результаты и обсуждение

Для оценки влияния плотности заполнения конечного элемента вокселями были решены тестовые задачи, результаты которых сравнивались с результатами решения в пакете Ansys 14.5 .

Тестовые задачи

Для оценки влияния плотности заполнения конечного элемента вокселями были решены тестовые задачи для одного конечного элемента в условиях различного нагружения. Рассмотрим полученные результаты для нагружения сжимающей силой: к верхней грани прикладывалась нагрузка P = — 400Н, равномерно распределённая по четырём узлам; нижние узлы фиксировались в перемещениях по трём направлениям, модуль Юнга составлял 2 ГПа, коэффициент Пуассона – 0,3 , размер куба – 10 х 10 х 10мм.

Варьируя величину вокселей и устанавливая в каждом из них значение из данных компьютерной томографии, равное единице, произвели серию численных экспериментов для сплошного материала. В табл. 1 отображены количество вокселей и их соответствующие размеры, используемые при расчётах.

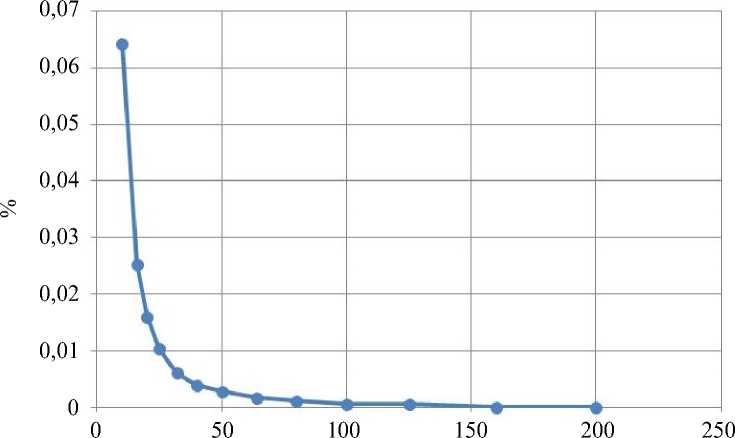
На рис. 2 приведены результаты, полученные численным интегрированием методом центральных прямоугольников для сплошного изотропного материала с использованием разного количества вокселей внутри конечного элемента.

Таким образом, при увеличении количества вокселей решение стремится к результатам, полученным в программном комплексе Ansys . Исходя из зависимости времени выполнения программы от количества вокселей внутри конечного элемента, можно сделать вывод о том, что для наиболее эффективного решения (оптимального по точности и времени выполнения) предпочтительно использовать порядка 50 вокселей на стороне куба. Результаты для других случаев нагружения конечного элемента аналогичны.

С целью оценки влияния густоты сетки при постоянной плотности компьютерной томографии были решены тестовые задачи для одноосного сжатия и изгиба. Задача ставилась для геометрии в виде параллелепипеда с одним характерным размером. В этом случае на одном торце фиксировались все перемещения в узлах, на противоположном – прикладывалась распределённая по узлам нагрузка (см. рис. 3).

Рассматривался образец со следующими параметрами данных компьютерной томографии: количество вокселей в направлении осей Ox , Oy , и Oz - 100 х 500 х 100 соответственно, размер вокселя - 0,2 х 0,2 х 0,2 мм. Свойства материала использовались из предыдущей тестовой задачи. Параметры конечно-элементной сетки приведены в табл. 2. Исследовались отдельно два вида нагружения: влияние сжимающей нагрузки вдоль оси Oy и действие изгибающей силы в направлении оси Oz (решение для силы, действующей вдоль оси Ox , аналогично в силу симметрии).

На рис. 4 отображены результаты, полученные для трёх видов конечноэлементной сетки. Следует отметить, что относительная погрешность решения несущественно зависит от количества вокселей внутри одного конечного элемента, что позволяет в допустимых пределах изменять размер и количество конечных элементов с целью лучшей аппроксимации геометрии.

Таблица 1

Количество вокселей на ребре куба и их соответствующие размеры

N vox	10	16	20	25	32	40	50	64	80	100	125	160	200	–
S vox , мм	2	1,25	1	0,8	0,625	0,5	0,4	0,3125	0,25	0,2	0,16	0,125	0,1	–

а

б

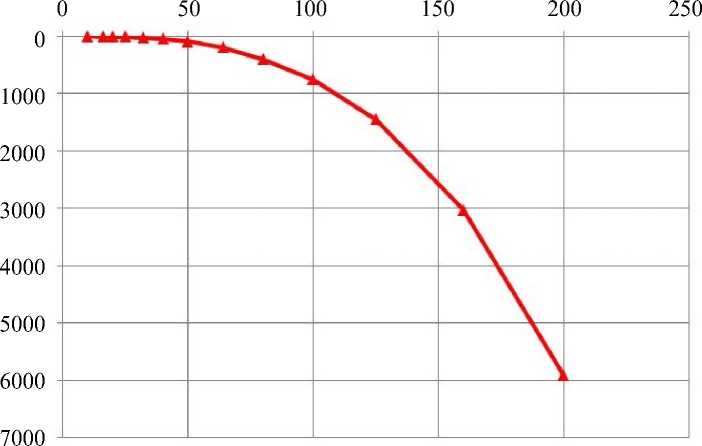
Рис. 2. Результаты численных расчётов: а – относительная погрешность значений перемещений для узлов с приложенной нагрузкой; б – время выполнения программы, с; ось абсцисс – количество вокселей по одной координате

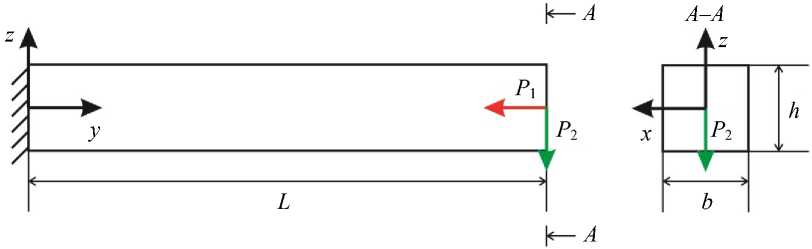
Рис. 3. Расчётная схема: P 1 , P 2 – прикладываемая сила; b , L и h – параметры геометрии в направлении осей Ox , Oy и Oz соответственно

Таблица 2

Параметры конечно-элементной сетки

Nh КЭ	NL КЭ	Nb КЭ	Количество вокселей в одном конечном элементе
1	5	1	1003
2	10	2	503
3	20	4	253

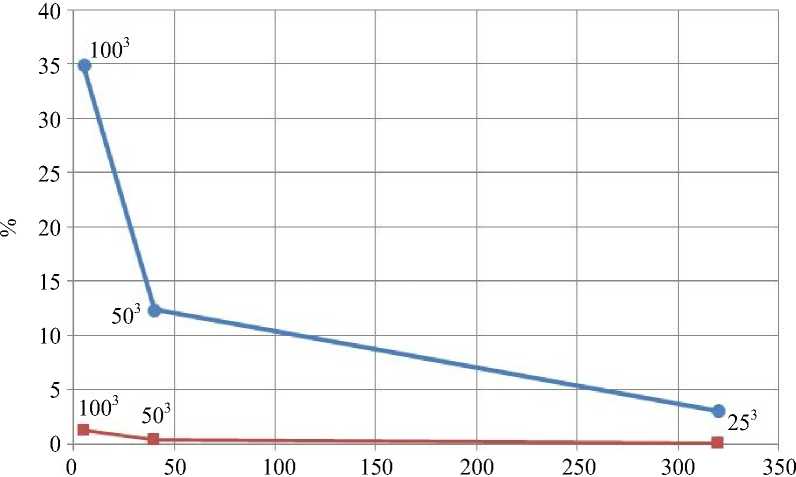
Рис. 4. Относительная погрешность значений перемещений для узлов с приложенной нагрузкой: красная линия – результаты для модели в условиях действия сжимающей нагрузки, синяя линия – под действием изгибающей силы; ось абсцисс – количество конечных элементов

Модельная задача

В модельной задаче использовались данные компьютерной томографии для диафиза бедренной кости крысы (рис. 5, а ). Сканирование выполнялось с применением микро- и нанофокусной системы рентгеновского контроля для компьютерной томографии и 2 D -инспекции Phoenix V|tome|X S 240 в лаборатории рентгеновской компьютерной томографии Института геологии и нефтегазовых технологий Казанского (Приволжского) федерального университета. Система оснащена двумя рентгеновскими трубками: микрофокусной с максимальным ускоряющем напряжением 240 кВ мощностью 320 Вт и нанофокусной с максимальным ускоряющем напряжением 180 кВ мощностью 15 Вт. Для первичной обработки данных и создания объёмной (воксельной) модели образца на базе рентгеновских снимков (проекций) использовалось программное обеспечение datos|x reconstruction . Зафиксированный в держателе образец помещался на вращающийся столик камеры рентгеновского компьютерного томографа на оптимальном расстоянии от источника рентгеновского излучения. Съёмка проводилась при ускоряющем напряжении 90–100 кВ и токе 140–150 мА. Размер исследуемой области - 4,21 х 3,46 х 5,89 мм, количество вокселей в направлении соответствующих координатных осей Ox , Oy и Oz - 624 х 512 х 874, размер вокселя -6,747 х 6,747 х 6,747 мкм.

а

б

в

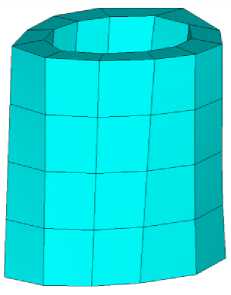
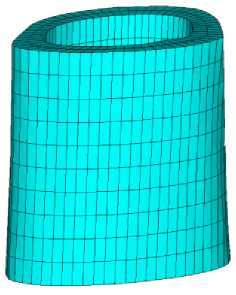
Рис. 5. Исследуемый образец диафиза бедренной кости крысы: а – представление данных компьютерной томографии; б – сетка 1; в – сетка 3

В табл. 3. отображены параметры расчетных конечно-элементных сеток, а на рис. 5, б и в приведены конечные элементы для сетки 1 и 3 соответственно. Узлы нижнего торца фиксировались в перемещениях по трём направлениям, на верхнем торце прикладывалась равномерно распределённая по узлам продольная сжимающая сила, равнодействующая которой равна P = - 400 Н. Модуль упругости Юнга принимался равным 30 000 МПа, коэффициент Пуассона – 0,3.

На рис. 6, а и б приведены распределения осевых перемещений, полученных с использованием двух типов конечно-элементных сеток.

На сетке с меньшим количеством конечных элементов (первая сетка) значения перемещений усредняются одним конечным элементом по толщине, при дискретизации по толщине двумя конечными элементами (для второй и третьей сеток) порядок аппроксимации распределения перемещений на торце повышается. На рис. 6, в показаны доверительные интервалы средних перемещений узлов верхнего торца объекта для конечно-элементных сеток различной густоты, увеличение стандартного отклонения объясняется увеличением количества узлов на исследуемом торце и, как следствие, изменением формы его деформированного состояния. Время выполнения расчетов составило: сетка 1 – 3,07 ч, сетка 2 – 3,16 ч, сетка 3 – 3,53ч. Видно, что затраченное время реализации алгоритма решения задачи на ЭВМ для различных сеток сопоставимо. Это объясняется тем, что формируемые матрицы жесткости конечного элемента для разных сеток вычисляются в одних и тех же квадратурных точках. Однако эта ресурсозатратная операция для конкретной расчетной области проводится только один раз, а при дальнейших расчетах сформированная ранее матрица жесткости просто считывается с носителя информации.

Таблица 3

Параметры разбиения на конечно-элементную сетку

N КЭ	Сетка 1	Сетка 2	Сетка 3
По толщине	1	2	2
По высоте	4	10	10
В окружном направлении	11	30	60

–0,043 –0,035 –0,03 –0,025 –0,02 –0,015 –0,01      0 –0,16    –0,12 –0,1 –0,08 –0,06 –0,04        0

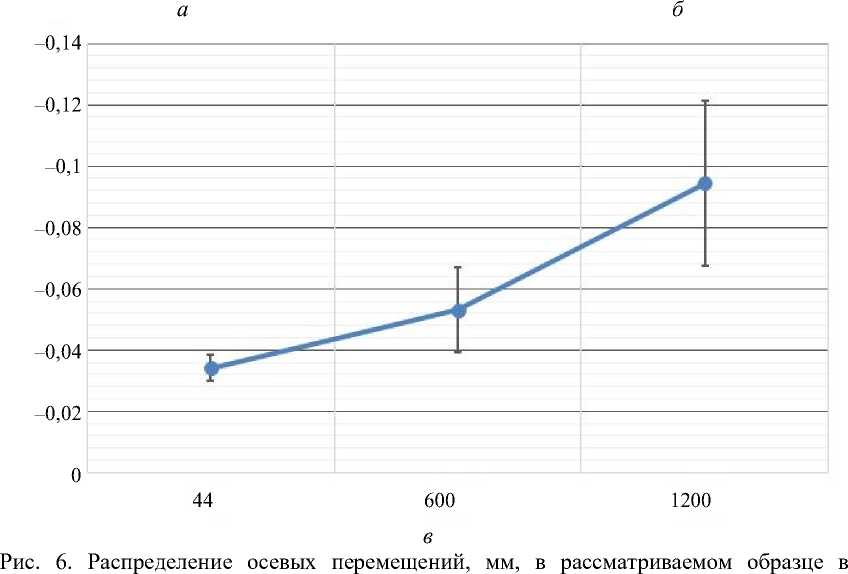
условиях действия равномерно распределённой по узлам сжимающей нагрузки: а – сетка 1; б – сетка 3, в – среднее продольное перемещение верхнего торца со стандартным отклонением при различном разбиении (ось абсцисс – количество конечных элементов)

Заключение

• 1.    В работе представлен один из возможных численных подходов к описанию процессов деформирования гетерогенных сред под действием внешних нагрузок, основанный на моделировании структуры расчетной области с учетом данных ее компьютерной томографии.

• 2.    Для оценки влияния данных компьютерной томографии на сходимость предложенной численной методики были решены тестовые задачи. Полученные результаты применялись для определения подходящих параметров (числа вокселей в конечном элементе) модельной задачи.

• 3.    Полученные численные результаты отображают влияние точности аппроксимации геометрии образца, а также иллюстрируют зависимость поля перемещений и напряженно-деформированного состояния от структуры материала.

• 4.    Данный подход позволяет исследовать поведение пористого материала под действием внешних нагрузок на основе оптической плотности материала. Исследования могут быть расширены с использованием другого вида обработки данных компьютерной томографии, путем усовершенствования формулы численного интегрирования локальной матрицы жесткости, а также с применением иных типов конечных элементов. Вопрос построения полей напряжений и деформаций остался вне рамок исследований данной работы, поскольку прямое построение напряженно-деформированного состояния в рамках предложенной модели метода конечных элементов проводится легко и однозначно, но возникает вопрос достоверности полученных результатов. Вполне возможно, что наилучшую точность можно будет получить путем осреднения напряженно-деформированного состояния, вычисленного в вокселях, но этот дискуссионный вопрос требует дополнительных экспериментальных исследований.

Благодарности

Публикация осуществлена при финансовой поддержке РФФИ и Правительства Республики Татарстан в рамках научных проектов № 18-41-160025 и № 18-41-160018.

Авторы выражают отдельную благодарность сети независимых диагностических центров «Пикассо».