Построение минимального доминирующего множества при проектировании wi-fi-сети

В современном мире технология беспроводной передачи данных становится предпочтительной, а в некоторых случаях и единственно возможной для коммуникации информационных устройств. Все более востребованной становится беспроводная связь в зонах большой плотности клиентов. Требуется эффективное использование радиоспектра и правильное проектирование сети.

На рисунке 1 представлена контекстная диаграмма процесса проектирования и построения беспроводных сетей. Одним из ключевых компонентов представленной диаграммы являются данные о зоне и площади покрытия территории, охваченной Wi-Fi-сетью. Если стоит задача в охвате сетью большого пространства со сложной конфигурацией возникает необходимость рационально разместить несколько Wi-Fi-излучателей, которые позволят обеспечить устойчивую связь с каждой точкой возможного расположения приёмника сигналов.

В результате получаем достаточно сложную комбинаторную задачу, решению которой посвящена эта работа.

Закон о связи Требования

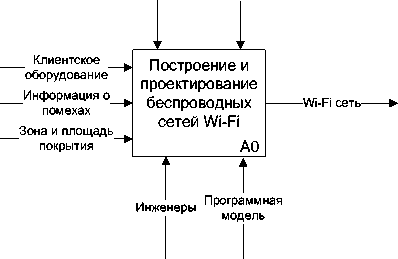
Рисунок 1. Контекстная диаграмма процесса проектирования и построения беспроводной сети

• Figure 1.    Designing and constructing of wireless network process context diagram

Постановка задачи и вопросы тестирования алгоритма её решения

Изначально будем предполагать, что в нашем распоряжении имеется модель, позволяющая определить зону охвата устойчивой связью Wi-Fi-излучателем при заданной пространственной точке его размещения. Разработка такой модели также представляет собой сложную задачу, но решается она совсем иными методами и выходит за рамки предлагаемой работы. Обозначим:

S ( x ) – область пространства, охваченная излучателем, помещённым в точку х ;

T – территория, подлежащая охвату.

Тогда задача формулируется следующим образом: определить дискретное множество D c T точек размещения излучателей, удовле- творяющего условию

|D | ^ min

T £ U S ( x )

x е D

Иными словами, необходимо определить положения всех излучателей, полностью покрывающих заданную территорию, причём количество излучателей должно быть минимально.

Очевидно, что, полагая T непрерывным множеством пространственных точек, мы получаем совершенно неподъёмную многомер- ную вариационную задачу, поэтому упростим её, перейдя к дискретной аппроксимации. Для этого достаточно допустить, что T и S(x) представляют собой дискретные множества неких опорных точек, расположенных на заданной территории. В такой постановке мы получим хорошо известную задачу о наименьшем покрытии (ЗНП), которая в теоретико-множественной интерпретации имеет следующую формулировку [1]. Даны множество T = {t1, … tM } и семейство S = { S1, …, Sn} подмножеств Sj c T. Каждому Sj поставлена в соответствие положительная стоимость сj. Необходимо определить подсемейство { S1, .., S„} c S, такое, что m

и при этом суммарная стоимость под-

T £ USk i=1 k *

семейства j m ^ минимальна.

Для разработки методов решения ЗНП обычно прибегают к её матричной интерпретации, которая состоит в следующем. Дана матрица A, состоящая из 0 и 1, размера m х n, в общем случае m ф n , и набор положительных стоимостей с j , j = 1, … n каждого столбца. Необходимо найти такое наименьшее множество S столбцов матрицы, при котором каждая строка матрицы содержала 1 хотя бы в одном из выбранных столбцов и сумма их стоимостей была минимальна.

Если A квадратная, её транспонированную матрицу A^T можно интерпретировать как матрицу смежности некоторого графа. В случае когда в A на главной диагонали стоят 1, а все с j = 1 ЗНП сводится к задаче о наименьшем доминирующем множестве (ДМ) графа.

Доминирующее или внешне устойчивое множество графа G = ( V , E ) – такое множество U вершин, что любая вершина из V \ U смежна с какой-нибудь вершиной из U . Иными словами ∀ u ∈ V \ U ∃ v ∈ U : ( v , u ) ∈ E . ДМ называется минимальным , если его подмножество уже не является доминирующим. ДМ называется наименьшим , если среди всех доминирующих множеств оно обладает наименьшей мощностью.

Задача о наименьшем ДМ практически во всех модификациях относится к классу NP -полных задач, исключение – построении наименьшего ДМ для дерева [1]. Лучший из комбинаторных методов решения общей ЗНП и пригодный для поиска наименьшего ДМ описан в[1]. Однако эффективность его невелика, максимальное число строк в матрице 30–40 элементов.

Более эффективны на практике методы ветвей и границ, основанные на булевской интерпретации ЗНП: минимизировать z = ∑ c _j x _j при ограничениях:

j

∑Aijxj≥1 ∀i=1,...,m, (2) j где xj = 1, если j-й столбец включён в S, и xj = 0 в противном случае.

Соответствующая программа bintprog входит в состав функций пакета оптимизации Optimization Toolbox системы Matlab. Её проверка на тестовых примерах построения наименьшего ДМ для графов, структура кото-рыхсоответствует задаче (1) показала её высокое быстродействие для графов с числом вершин не более 40. В некоторых случаях она позволяет решать за приемлемое время задачи значительно более высокой размерности, однако стабильность её работы оставляет желать лучшего. Это говорит о необходимости искать более быстродействующие приближённые алгоритмы.

Подробный обзор методов решения различных вариантов ЗНП и соответствующих тестовых примеров приведён в [2]. Для решения ЗНП предложено большое число точных алгоритмов, основанных на методе ветвей и границ, отсечения, перебора L -классов и др. Однако теоретические оценки вычислительной сложности этих методов сопоставимы со сложностью переборных алгоритмов. Это говорит о том, что выход следует искать в создании приближённых методов.

Согласно имеющейся классификации, множество тестовых задач можно разбить на три основные группы: задачи специальной структуры, прикладные задачи и задачи со случайными исходными данными. Однако структура приведённых в [2] задач первой и второй групп мало похожа на задачу (1) об охвате территории

Wi-Fi-сетью. А что касается третьей группы, то в задаче (1) A^T должна быть матрицей смежности связного графа, чего нельзя гарантировать при случайной генерации матрицы.

Таким образом, для тестирования алгоритма решения задачи (1) надо создавать специальные задачи. На наш взгляд, помимо практических задач, для которых точное решение неизвестно, наиболее подходят популярные задачи-головоломки, связанные с покрытиями: расстановка шахматных фигур, бьющих каждую клетку доски, покрытие клетчатого поля фигурами сложной конфигурации и т.п.

Предлагаемые алгоритмы

Для решения задачи (1) в рамках предлагаемой статьи были опробованы следующие пять алгоритмов.

• 1.    Точный алгоритм бинарного программирования с использованием программы bintprog. Этот алгоритм основан на методе ветвей и границ и в качестве релаксационной задачи [3] применяет задачу обычного линейного программирования (ЛП), решаемую двойственным симплекс-методом.

• 2.    Жадный алгоритм, описанный в [3], и основанный на следующей эвристике: на каждом шаге в графе G = ( V , E ) выбирается вершина максимальной степени, т.е. доминирующая над наибольшим числом смежных вершин. В результате имеем следующий алгоритм: Шаг 1. Первоначально множество D (текущее доминирующее множество) полагается пустым. Шаг 2. Пока V ≠ ∅ выбрать в G вершину максимальной степени. Выбранная вершина вместе со своими рёбрами удаляется из G и добавляется в D .

• 3.    Алгоритм локальных вариаций. Это приближённый метод, предложенный в [4] для решения задач целочисленного и булевого программирования. Он основан на последовательном улучшении решения за счёт поиска лучшего варианта в локальной окрестности некоторой начальной точки x ⁰. В качестве условия, ограничивающего размер окрестности, предложено j^ k , - х 0| ^ r при небольшом значе- i = 1

• 4.    Алгоритм экстраполяции [5]. Модификация этого алгоритма была использована для построения рационального ветвления в методе ветвей и границ. Суть алгоритма состоит в разбиении области допустимых решений задачи ЛП на примерно одинаковые по объёму области и продолжении решения на всю область.

• 5.    Модифицированный жадный алгоритм, – метод предложенный авторами работы. Он основан на следующей эвристике. Недостаток обычного жадного алгоритма в том, что на начальном этапе он выбирает все хорошие точки, а в конце вынужден «проводить зачистку», т.е. добирать оставшиеся вершины с малыми степенями.

Этот алгоритм можно использовать как для построения вершинного покрытия, так и доминирующего множества. В [3] показано, что при решении задачи о минимальном вершинном покрытии, алгоритм имеет теоретически неограниченную относительную погрешность. Иными словами, если обозначить F^opt и F^прибл – значения целевой функции в точном и приближённом решении, соответственно, то при любой константе K > 0 можно предложить задачу о минимальном вершинном покрытии, для которой решение, полученное жадным алгоритмом, удовлетворяет условию

F прибл opt

- F

Для задачи о наименьшем ДМ таких данных найти не удалось, однако, при тестировании этого алгоритма максимальная наблюдаемая относительна погрешность составила 30%, что достаточно много.

нии r = 1, 2, 3. Для булевских переменных в данную окрестность должны входить все точки, отличающиеся от текущего центра x ⁰ не более чем r координатами. Каждый раз при нахождении лучшей точки в неё переносится центр окрестности и поиск продолжается. Если при максимальном r лучший вариант не будет найден – алгоритм заканчивает работу, текущий центр считается решением.

Нетрудно заметить, что эффективность алгоритма во многом зависит от удачного выбора начальной точки, при везении можно найти точное решение. Поэтому теоретические оценки качества алгоритма отсутствуют и его можно проверить только тестированием.

Авторы предлагают несколько начальных вершин задавать принудительно, независимо от их степени, а последующие вершины выбирать в соответствии с жадной стратегией. Выбирать начальные вершины можно случайно и проделать такие пробы достаточно много раз, порядка 1000 попыток.