Построение минимальной параметрически заданной поверхности методом минимизации интеграла Дирихле

DOI:

В современном мире уравнения минимальной поверхности получили широкое распространение в таких смежных науках, как биология, механика и математическая физика, и сыграли незаменимую роль в таких прикладных отраслях производства, как архитектура и строительство [13].

Первым, кто проложил дорогу к изучению минимальных поверхностей, был Жозеф Плато (1801–1889). Опыты Плато заключались в конструировании мыльных пленок, затягивающих проволочные контуры. При извлечении замкнутого контура из мыльного раствора на нем образуется радужная мыльная пленка, ограниченная контуром. Ее энергия пропорциональна площади. Поэтому жидкая пленка превращается в эластичную поверхность, стремящуюся минимизировать свою площадь. Так, из работ физика Жозефа Плато выросла теория минимальных поверхностей, ставшая важнейшей областью в вариационном исчислении. «Проблема Плато» формулируется следующим образом: верно ли, что на любой замкнутый контур можно натянуть минимальную поверхность, и если «да», то сколько таких поверхностей и каковы их топологические свойства. Важные результаты в этом направлении были получены А.Т. Фоменко [16], Р. Курантом [7], Т. Радо [18], Д. Дугласом [15], В.М. Миклюковым, В.Г. Ткачевым, А.Д. Веденяпиным [2; 8–10] и другими [14; 17].

В своей статье при решении задачи Плато в классе полиномиальных отображений мы отталкиваемся от работы [6]. В работе [7] исследуется вопрос о равномерной сходимости полиномиальных приближенных решений уравнения минимальной поверхности, построенных с помощью алгебраических многочленов. В работе [4] дано описание численной реализации метода конечных элементов, основанного на кусочно-линейных функциях. В работе [6] доказана равномерная сходимость полиномиальных решений в плоских областях. Целью данной работы является разработка и реализация алгоритма для вычисления и построения минимальной поверхности для различных граничных контуров Г с использованием математического пакета для численного вычисления на языке Python. Широкий функционал программы удобен для реализации чиcленного расчета, описанного в парадигме процедурного программирования. А благодаря своему широкому распространению и простоте интерфейса позволяет решать задачи, связанные с прикладной математикой.

1.    Постановка задачи

Рассмотрим плоскость с декартовыми координатами и, v. Пусть B круг единичного радиуса с центром в начале координат. Обозначим через S параметрически заданную поверхность радиус-вектором г = f(u,v), где u,v Е В . Будем считать, что координаты вектора г являются гладкими функциями х = x(u,v), у = y(u,v), z = z(u,v). Таким образом:

г = х(и, v)i + у(и, v)j + z(u, v)k.

Известно [7], что поверхность S является минимальной, если выполнены следующие условия:

△ г = 0,                                      (1)

где

E - G — 0,F = 0,

△^г — ^г uu + ^г w , ^E  x u + у _u + z u ,

G — x\ + ух. + z\,F — X u X _v + y _u y _v + Z u Z _v .

Рассмотрим следующую задачу (задача Плато): требуется построить минимальную поверхность S , имеющую в качестве границы заданную в пространстве кривую Г. Другими словами, нужно найти такую вектор-функцию f(u,v), удовлетворяющую условиям (1), (2) и отображающую непрерывную границу области B на кривую Г. Отметим, что в работе [7] показано, что вектор-функция, доставляющая минимум функционалу

¹ (^) = И (f u2 + f 2 )dudv — Ц (x ² u + y 2 u + z²u + x\ + у\ + z\ ) du dv (3)

в

в

при фиксированных граничных условиях на функции x(u,v),y(u,v), z(u,v), задает минимальную поверхность. Более того, решение этой вариационной задачи существует. Сформулированная нами вариационная задача может быть заменена следующей эквивалентной задачей для вектора f(u,v) с 3 компонентами x(u,v),y(u,v), z(u,v), В — единичный круг u ² + v ² <  1 с границей С : u ² + v ² — 1. Требуется найти минимум интеграла Дирихле (3). Будем рассматривать в единичном круге В плоскости u,v векторы г с 3 компонентами x(u,v),y(u,v), z(u,v), обладающими внутри круга кусочно-непрерывными производными, непрерывные в замкнутом единичном круге В U C и взаимно-отображающие непрерывную границу С единичного круга на заданную кривую Г трехмерного пространства г. Среди этих векторов требуется найти тот, для которого интеграл Дирихле

О[г] — Ц (f в

+ гЦ) du dv

принимает минимальное значение d.

2.    Способ решения

Пусть задана некоторая вектор-функция ф : В о R ³ , являющаяся взаимно-однозначным отображением круга В на пространство R ³ . Ее сужение на окружность дВ будет задавать граничный контур Г. Контур Г в таком случае является не слишком сильно изогнутым, то есть его можно взаимно-однозначно спроектировать на выпуклый контур (окружность). Известно, что в таком случае существует одна и только одна минимальная поверхность, затягивающая данный контур [12]. Для приближенного решения поставленной задачи будем использовать вектор-функции вида

п

f(u, v) — ^f (u, v) + (1 — u — v ² ) ^ Cijtfv ¹ .

i,j=0

В этом случае при изменении коэффициентов cij значения вектор-функции г изменяются во внутренних точках круга В, но не изменяются на его границе. Тогда пп rU(u,v) = CU(u, v) + (1 — и2 — v2) ^ cijiu^v^ — 2 ^ cijui+1vj, i,j=0

пп rV(u,v) = ФV (u,v) + (1 — u2 — v2) £ cij ju*vj-1 — 2 £ cijигvj+1.

i,j=0

Далее подсчитываем подынтегральное выражение в интеграле I(r):

22 u ¹ V

^ф u (u,v) + (1

-

и ²

— v2) £ c- i,j=0

-

2 £ c ij i,j=0

)

+

+

^^ф V (u,v) + (1

— u ² — v ² ) £ ецjMv - i,j=0

-

п             \ ²

£сц и* v ^j+1j .

После того как посчитаем выражение r„ + r², нужно проинтегрировать его по кругу В. Подынтегральное выражение представляет собой линейную комбинацию функций вида u ^k v^l . Поэтому интегралы от этих функций по единичному кругу вычисляются. В итоге после вычисления интеграла получим квадратичное выражение относительно искомых коэффициентов c _ij . Нам нужно найти такой набор значений этих коэффициентов, на котором достигает минимума этот интеграл. Для этого вычисляем производные д^- , приравниваем их к нулю и получаем линейную систему алгебраических уравнений.

В итоге после решения этой системы получим конкретную вектор-функцию, которая и будет приближенно описывать искомую минимальную поверхность.

3.    Алгоритм решения

Итак, мы имеем приближенное решение поставленной задачи, представленное вектор-функцией:

п

r(u, v) = ф(«, v) + (1 — u ² — v²) ^ c _ij u ⁱ v ^j .

i,j=0

Введем обозначения A^(u, v) = (1 — u ² — v ² )uⁱv ^j , где i,j = 0 .. .n. Тогда

/              п        \2/              п\ r„ + rV = {Cu(u,v)+^cij Aij\ + I Cu(u,v) + ^J cijAij ] .

\             i,j=0       U u    \             i,j=0

Проинтегрировав выражения по единичному кругу В , получаем:

//(r U + ^rA dudv = £ с^2B ijij

JBJ                     К)=0

О £ -2_Г ( (d^{C (} u^{,v )} V / dfy^v) у\

—2 кАc+Ц д- ));

+ 2С00С01В0002 + 2cqoCQ2 В0002 + . . . + 2С(п—1)пСпп В(п—1) ппп’ г д'    В„ = JJK ^)'- (^)-) d.d..

_д [[ д^{дА ( ( U,v} ) ^9А Р<1 (^U’^{V ) В —} JJ ^^“     aUT~

В

+

dA jj (и, v ) дA pg (и, у) дv дv

)

du dv,

^{C —}-4

дAij (и, v) дф(и, v) дAij (и, v) дф (и, v) \ ди ди        dv dv J du dv.

Вычисляя производны' по каждой компонент' векторов c _ij , приравниваем их к нулю и получаем линейную систему алгебраических уравнений:

^С 00 ^В 0000 ^{+ С} 01 ^В 0001 ⁺ • • • ^{+ С} п0 ^В 00п0 ⁺ • • • ⁺ С _Пп ^В00гт — C oo

^С 00 ^В 0100 ^{+ С} 01 ^В 0101 ⁺ • • • ^{+ С} п0 ^В 01п0 ⁺ • • • ^{+ С} пп ^В 01пп ^{— С} 01

^С 00 ^В пп00 ^{+ С} 01 ^В пп01 ⁺ • • • ^{+ С} п0 ^В ппп0 ⁺ • • • ^{+ С} пп ^В пппп

С! ^ пп .

Стоит заметить, что система является симметричной относительно главной диагонали, так как В _ij_pg — В _pgij . А размерность матрицы (п + 1) ² . Все полиномы в интегралах В _ij_pg являются линейными комбинациями и соответственно вычисляются. Таким образом, задача Плато сводится к вычислению всех интегралов В _ij_pg и C _ij на единичном круге и решению линейной системы алгебраических уравнений размерности (п + 1) ² .

4.    Вывод рекурентной формулы

Все интегралы вида

Г Г ( дA ij ( u,v ) дА рд ( u,v )

J J \ ди ди

В

+

дA ij (u,v) дА _Рд ( u,v ) дv дv

)

du dv

не зависят от вектор-функции . Поэтому нахождение всех таких интегралов можно свести к явному виду. Найдем общий вид полинома дAij (и, v) дАрд(u,v) ди ди

+ дA ij ( u,v ) дА рд ( u,v ) дv дv

— u ^t+g+2 v ^j+p (2q + 2i + 2р + 2j + 4 + ip + 2jp) +

+ и^г+д v^{B p +2}(2q + 2i + 2p + 2j + 4 + ip + 2jp) + + и^{г +д} v^j+p(-2q - 2i - 2p - 2j - 2iq - 2jp) +

+ iqu ^i+g—2 v ^j+p+4 + iqU ^g '²v ^{j p} + j^^g v^P ^-2 +

+ ipu^{i +g+4} v^{j +}P- ² - 2iqu ^{i+g — 2} v ^{j+p — 2} - 2jpu ^i+g+2 v ^{j+p — 2} .

Так как интегрируем выражение по единичному кругу, можно перейти к полярной системе координат:

Ц u ⁿ v ^m dudv = в

1    2 п

J 0 Jo

ρ

n+m+1

sin ⁿ a cos ^m a d a d p .

Далее положим

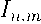
1    2 n

ρ

n+m+1

sin ⁿ a cos ^m a d a d p .

Поскольку пределы интегрирования не являются функциями, можно переписать интеграл в виде:

= / p ^n+m+1 d p I sin ⁿ a cos ^m a d a 00

n + m + 2

2 n

L ^{sin n}

a cos ^m a d a .

Рассмотрим интеграл: J _n,_m = 0 ⁿ sin ⁿ a cos ^m a d a . Если хотя бы одна из степеней n или m будет нечетной, он будет равняться нулю. Проинтегрируем по частям данный интеграл, занеся под дифференциал cos a :

2 n

J _n,_m = J   sin ⁿ a cos ^m-1 a d(sin a ) =

2 n

= sin ⁿ⁺¹ (a) cos ^n-1 a | 0 ^% — j (n sin a ⁿ⁺¹ cos ^m-1 a — (m — 1) sin ⁿ a cos ^m a) d a .

Так как при двойной подстановке sin ⁿ⁺¹ acos ^n-1 a | 2 ⁿ = 0, перепишем интеграл в рекуррентной форме:

J.

n + 1

Т ^J n+2,m - 2 ^. m — 1

Таким образом, j T^m — (2i — 1) Г2п . n+m , Jn,m =Дп + (2i — 1) I sin ada, где m — четное. Аналогично запишем рекуррентную формулу для

/- 2п

^J n,m    /

■ n+m , ^{n + m} - ¹ , sin ⁺ a d a =--------- J _{nm- 2}

n + m или

J

(n+m)/2

∏︁ г=1

n + m — (2i — 1)

n + m + (2i — 2)

2 п ,

где (n + m) нацело делится на 2.

Суммируя вышеперечисленное, получаем:

1    2 п

ρ

n+m+1

sin ⁿ a cos ^m a d a d p

2n     1ПГ m — (2i — 1) ^pt )/ ² n + m — (2i — 1)

n + m + 2 n + (2i — 1)        n + m + (2i — 2)

В случае п = 0 или т = 0 считаем интеграл как рекуррентную формулу для sin ” а и cos’ ” а соответственно:

1 ”,о

1   2 π

=L L ^р' +

sin ” а d a d p

2п ”/2 п - (2i - 1) п + 2 п - (2i - 2) ’

1    2 π

2 п ГТ т - (2i - 1) т + 2 ^=1 т - (2i - 2)

h ,т = J J  Р^{т +}1 cos ” а d a d p

Таким образом, алгоритм вычисления полиномиальных функций подынтегрального выражения сводится к нахождению для каждого i,j,p и q линейной комбинации, а также интеграла от функции u^lv ^k через рекуррентную формулу. При этом точность вычисления является максимальной, что полностью освобождает от необходимости применять методы для приближенного численного интегрирования.

5.    Оптимизация алгоритма, связанная с четностью подынтегральных выражений

Как упоминалось ранее, подынтегральное выражение B tj_pq , интегрируемое на единичном круге, имеет ряд особенностей. Так, например, это выражение будет всегда равно нулю, если i и j не имеет кратность два. Каждый раз, когда рассматриваем линейную комбинацию u^lv ^k , будем выбирать такие степени, где I mod 2 = 0 и к mod 2 = 0. Рассмотрим пример для п = 1. Для удобства записи будем использовать вместо четырех индексов i,j,p,q два индекса k,t:

к = i(n + 1) + j,t = р(п + 1) + q.

Это возможно, так как в ранней записи матрицы B индексы i,j представляли собой не два разных числа, а одно в системе счисления с основанием (п + 1). Таким образом, число ij можно преобразовать по вышеуказанным формулам в число к в десятичной системе счисления. Аналогично для индексов р, к:

B ₀ , ₀ = 4u ² + 4v ² , B ₀ ,1 = 6u ² v + 6v 3 - 2v,

B ₀ , ₂ = 6u 3 + 6uv 3 - 2u, B ₀ ,3 = 8u ” + 8uv 3 - 4uv,

B 1, ₀ = 6u ² v + 6v 3 - 2v, B 1,1 = 4u ⁴ + 10u ² v ² - 2u ⁺ 9v ⁴ - 6v ² + 1,

• B 1, ₂ = 8u 3 v + 8uv 3 - 4uv, B^ = u⁵ + 12u 3 v ² - 2u 3 + 11uv ⁴ - 8uv ² + u,

B ₂ , ₀ = 6u 3 + 6uv 3 - 2u, B ₂ ,1 = 8u 3 v + 8uv 3 - 4uv,

B ₂ , ₂ = 9u ⁴ + 10u ² v ² - 6u ⁺ v ⁴ - 2v ² + 1, B ₂ ,3 = 11u ⁴ v + 12u ² v ³ - 8u ² v + v ⁵ - 2v ³ + v, B 3, ₀ = 8u 3 v + 8uv 3 - 4uv, B 31 = u⁵ + 12u ³ v ² - 2u 3 + 11uv ⁴ - 8uv ² + u,

B 3, ₂ = 11u ⁴ v + 12u ² v ³ - 8u ² v + v ⁵ - 2v ³ + v, B 3,3 = u ⁶ + 15u 4 v ² - 2u ⁴ + 15u ² v ⁴ -- 12u ² v ² + u ² + v ⁶ - 2v ⁴ + v ² .

С учетом ограничений на степени можно переписать матрицу B в виде:

^B 0,0 = ^{4 u} 2 ^{+ 4 v} 2 , ^B 0,1 = ⁰ , ^B 0,2 = ⁰ , ^B 0,3 = ⁰ ,

B 1, ₀ = 0, B 1,1 = 4u ⁴ + 10u ² v ² - 2u ⁺ 9v ⁴ - 6v ² + 1, B 1, ₂ = 0, B 1,3 = 0,

B 2,0 = 0, B 2,1 = 0, B 2,2 = 9u ⁴ + 10u ² v ² - 6u ⁺ v ⁴ - 2v ² + 1, B 2,3 = 0,

B 3, ₀ = 0, B 3,1 = 0, B 3, ₂ = 0, B 3,3 = u ⁶ + 15u 4 v ² - 2u ⁴ + 15u ² v ⁴ - 12u 2 v ² + u ² + v ⁶ - 2v ⁴ + v ² .

Или

	/ vol   0	00
В =	0 vol 0    0 0    0 vol 0		, где vol — некоторая линейная комбинация и и v. Для
	00	0 vol /
п = 2 вид матрицы будет немного другой:
		/ vol   0	vol 0    0    0 vol 0 vol\
		0 vol 0    0    0    0    0 vol 0
		vol 0	vol 0    0    0 vol 0 vol
		00	0 vol 0 vol 0    0    0
В =		00	0    0 vol 0    0    0    0	.
		00	0 vol 0 vol 0    0    0
		vol 0	vol 0    0    0 vol 0 vol
		0 vol 0    0    0    0    0 vol 0
		\ vol   0	vol 0    0    0 vol 0 vol /

На индексы г, j, q и р можно наложить условие: если i + q mod 2 = 0 и j + р mod 2 = 0, то В = 0, иначе считаем интеграл по рекуррентной формуле. Так как интеграл на единичном круге от нечетной функции всегда равен нулю, мы можем частично предсказать результат и для интеграла, содержащего ϕ. В общем виде мы будем по отдельности сравнивать ((1 — и ² — v ² )и^) _и и ф(и,v). Если хотя бы одна из функций четная, а другая нет, то интеграл на единичном круге будет равен нулю, в противном случае вычисляем его. Аналогично и для ((1 — и ² — v ² )u ^l v ^ ) _v и ф(и, v). Таким образом мы частично сократим алгоритм вычисления, что существенно для больших значений п.

6.    Реализация алгоритма на языке Python

Для реализации алгоритма нам необходимо ввести ряд вспомогательных функций, которые отвечали бы за вычисление линейных комбинаций и интегралов в явном виде. При написании кода, реализующего алгоритм минимизации поверхностей, использовалась библиотека NumPy для удобства хранения данных в виде массивов и реализации математических вычислений. За погрешность вычислений возьмем среднее значение разницы точного решения от вычисляемого для каждой координаты. Было выявлено, что, если уравнение координаты радиус-вектора исходной поверхности не отличается от координаты радиус-вектора минимальной поверхности, то погрешность вычисления этой координаты будет нулевой. Так как тестирование проводилось на поверхностях, где координаты радиус-векторов отличались от координат минимальной поверхности лишь на одно уравнение, можем принять за общую погрешность вычислений погрешность для изменяемой координаты. В приведенной ниже таблице представлены погрешности минимизации для разных поверхностей и степеней полиномиальной функции.

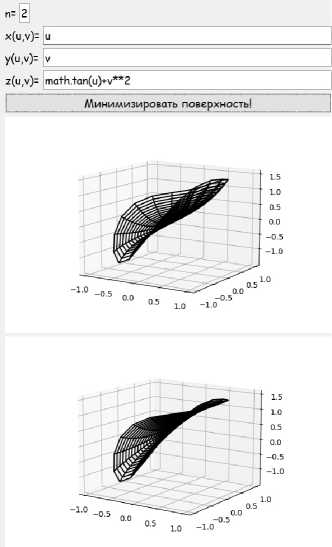
Программа была протестирована на различных поверхностях. На рисунках представлен интерфейс программы. В верхней части окна приложения пользователю предлагается ввести степень полиномиальной функции п и уравнения вектор-функции, далее необходимо нажать на кнопку «Минимизировать поверхность!». После этого в верхнем окне появляется график исходной поверхности, а в нижнем минимизированной.

Исходная поверхность		Минимизированная поверхность		n	Погрешность
( х(и, v) = и / у(и, v) =v (z(u,v) = u + v — и2				1	3.330e-17
		<	x(u^ V) = и y(u, v) = V z(u, v) = —^ + u+ + V + v — T
				2	3.330e-17
				3	3.330e-17
( x(u,v) = и < y(u, v) — V ( z(u, v) = uv + v2 + u2			' x(u, v) = и y(u, v) = V z(u, v) = uv + 1	1	2.220e-17
				2	2.220e-17
				3	2.220e-17
( x(u,v) = и < у(и, v) = v {z(u, v) = u2 + V2 + и		( x(u, v) = и < y(u, v) = V [z(u, v) = u + 1		1	2.359e-17
				2	2.359e-17
				3	2.359e-17
	' x(u, v) = и y(u, v) = V z(u,v) = arctg^)+ k +0.01(1 - it)2(l — v)2	<	x(u,v) = и y(u, v) = V z(u,v) - arctg(^)	1	0.0015721
				2	0.0010404
				3	0.0010404

Пример 3

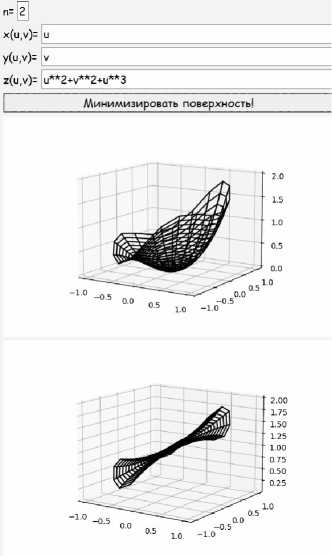
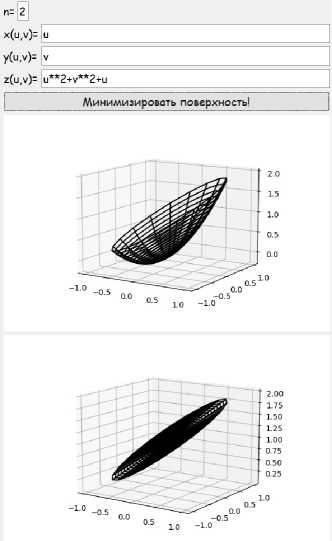
Пример 5

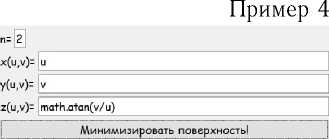
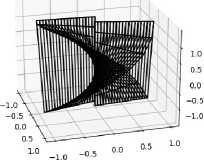
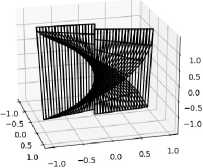
Пример 6

Заключение

На языке Python был реализован алгоритм, позволяющий рассчитывать приближенные минимальные поверхности в классе полиномиальных вектор-функций, заданных на единичном круге и удовлетворяющих краевому условию Дирихле (задача Плато). Бы- ли рассмотрены вектор-функции с различными граничными контурами Г. В примерах 1–5 были рассмотрены нетривиальные поверхности, которые после работы алгоритма минимизации переходят в приближенные минимальные поверхности. Также был рассмотрен случай минимизации уже минимальной поверхности и, как видно из примера 6, программа работает корректно и не изменяет поверхность, являющуюся минимальной. В таблице приведены погрешности вычислений для некоторых поверхностей. Можно заметить, что погрешность вычисления данной программы довольно мала, и для большинства поверхностей достаточно взять степень полиномиальной функции п = 1.