Построение модели многосвязного объекта на основе совместного использования данных и экспертных оценок

Одной из задач построения дескриптивных статических моделей многомерных многосвязных объектов является задача построения многомерных регрессионных зависимостей. Классический подход к решению этой задачи основан на использовании таблицы совместно наблюдаемых значений независимой и зависимой случайных величин.

На практике формирование таблицы совместно наблюдаемых значений может встречать определённые трудности. Это обусловлено, например, тем, что сбор различных данных осуществляется несколькими организациями, деятельность которых регламентируется разными документами. Либо тем, что происходят потери архивных данных. Либо вследствие того, что измерения параметров состояния сложных систем ранее не осуществлялись, но для их оценки можно использовать мнение экспертов. В качестве примера можно привести задачи, связанные с управлением дефектами в программных компонентах аппаратно-программных комплексов на разных стадиях их жизненного цикла [1].

Значения независимых и зависимых параметров могут задаваться в виде измерительных данных и в виде экспертных оценок разного вида: в виде ожидаемых значений; интервала возможных значений; совокупности ожидаемых значений и интервала возможных значений случайной величины. Разработка метода преобразования измерительных данных и экспертных оценок, задаваемых в разных формах, к виду таблицы совместно наблюдаемых значений, послужит основой построения многомерных регрессионных зависимостей.

1    Методы построения функциональных зависимостейна основе измерительных данных и экспертных оценок

Классическому подходу к построению регрессионных зависимостей можно поставить в соответствие схему

• (1)                          Л < ⁰ > :{х,у} " ^у = ф ₀( х, 9).

Здесь { х, z } " - множество совместно наблюдаемых значений компонент векторов независимой х и зависимой у величин;

ф₀ ( х , 9) - функциональная зависимость, задаваемая в параметрической форме;

N - число пар значений х и у.

В литературе описаны различные операторы Д(0), например, реализующие метод наименьших квадратов [2], либо метод наименьших модулей [3].

При решении практических задач, вследствие сложности организации сбора исходных данных, формирование {х, у} " может встретить серьёзные трудности.

В работе [4] описан подход к построению одномерных непараметрических строгих функциональных зависимостей на основе решения обратной задачи построения закона распределения функции случайного аргумента (прямая задача описана в [5]).

Схема решения обратной задачи имеет вид

• (2)                      Д⁽¹⁾: №), F(y')} ^ у = ф 1 (х),

где F(x), F(y) - оценки одномерных законов распределения независимой и зависимой случайных величин соответственно, определяемые на основе обработки выборочных данных

• (3)                         Д⁽²⁾: {х} " ^ х = F(х), Д⁽²⁾: {у} ^ ^ у = F(y).

Особенностью схемы (2) является то, что свойства выборочных данных {х} " , {у} ^ (объём, точность регистрации) могут быть различными. Ограничением схемы (2) является необходимость обоснования самого факта наличия строгих зависимостей, например, исходя из физического содержания задачи. В работе [5] приведены результаты исследования свойств оценок строгих функциональных зависимостей ^₁(х), получаемых посредством (2).

Если объёмы выборочных данных {х} " , {у} ^ являются большими в статистическом смысле, то в качестве Д⁽²⁾ могут использоваться «традиционные» методы, описанные, например, в [2, 5, 6]. Если же объём выборочных данных мал, а тип закона распределения априорно неизвестен, то в качестве Д⁽²⁾ целесообразно использовать методы, основанные на принципе максимизации энтропии [7-9]. Построение оценки закона распределения непрерывной случайной величины сводится к определению параметров ^ j выражения

• (4)                    f(z = ехр^.^ z^j) , j = 1n

в результате решения системы уравнений вида

• (5)                       J ^_zk ехр(^ _;^ j z^dz = v. ( ^k) ,

где z - непрерывная случайная величина;

{a_z , b_z } - границы интервала физически возможных значений случайной величины;

v^(k^- начальный момент к -го порядка, определяемый по выборочным данным.

При решении практических задач целесообразно ограничиться двумя первыми моментами [4]. Широко используемые на практике нормальный, показательный и равномерный законы распределения случайных величин, являются частным случаем выражения (4).

Экспертные оценки представляются в виде оценки ожидаемого значения случайной величины M[ z] и/или интервала возможных значений случайной величины Z (возможны следующие варианты представления интервалов: ze[a_z , b_z ]; ze[a_z, ^)) [10].

Если известны лишь границы интервала возможных значений случайной величины, т.е. ze [ a_z, b_z],то

• (6)                               Д⁽³ ) :[ a_z, b _z] ^ F⁽³⁾(z).

Здесь Д⁽³ ) представляет собой частный случай (5), когда k=0. В этом случае оптимальной оценкой F⁽³⁾(z) является равномерный закон распределения.

Если известны ожидаемые значения M\ z], а интервал возможных значений случайной величины представляется в виде [a_z, го), то построение оценки сводится к решению задачи

• (7)                                 Д ⁽⁴⁾: {M[z], [ a_z, го)} ^ F⁽⁴⁾(z).

Здесь Д(4) представляет собой частный случай (5) при k=1. Оптимальной оценкой F(4)(z) в этом случае является показательный закон распределения

• (8)                             F⁽⁴ ) (z) = 1 — е^{- Zz} .

Параметр закона распределения определяется соотношением Л = (М [z] — a _z)^-1.

Если известны М [z] и границы интервала [az, bz], то оценка закона распределения ищет- ся в результате решения задачи

• (9)                                 Д⁽⁵⁾: {M(z), [a_z,b_z]} ^ F⁽⁵ ) (z).

Оценка представляется в виде

• (10)                                  F⁽⁵ ) (z) = J^e ^м о ^+м i ^T dr,

причём параметры модели ц₀, ц_t находятся в результате решения системы уравнений

J^e ^м о ^+м 1 dr = 1

| J^r е м о ⁺ м i T d_T = M[z].

В частном случае, если дополнительно известно, что F^{(5 )}(a_z) = 0, F^{(5 )}(_b_z) = 1, F⁽⁵⁾(z)

представляет собой треугольное распределение.

Преобразование экспертных оценок к виду законов распределения непрерывных случайных величин делает возможным расширить схему (2) на случай построения одномерных не- параметрических регрессионных зависимостей на основе совместного использования изме- рительных данных и экспертных оценок.

Вместе с тем, методы построения функциональных зависимостей на основе решения обратной задачи построения закона распределения функции случайного аргумента, в том числе на основе совместного использования измерительных данных и экспертных оценок, ориентированы на исследование одномерных зависимостей и не адаптированы к исследованию поведения многомерных систем.

2    Построение многомерных регрессионных зависимостейна основе одномерных непараметрических регрессионных моделей

К числу статических моделей, используемых для описания многомерных безынерционных многосвязных объектов относятся многомерные регрессионные зависимости

• (12)                          У / = Ф j(xj ■ 1 ,-Xj _{к у} ) J = 1T/V,

где yj - компоненты вектора Y зависимой переменной;

^xj ij , ^' = 1; ^ 7 — компоненты вектора независимой переменной;

Ф5 (•) - зависимость (параметрическая либо непараметрическая) значений j -й компоненты вектора зависимой переменной от значений компонент вектора независимой переменной.

Классический подход к построению многомерных регрессионных зависимостей основан на обработке совместно наблюдаемых значений [5, 6], представленной в табличной форме (см. таблицу 1).

Таблица 1 – Головка таблицы совместно наблюдаемых значений независимой и зависимой переменных

Номер измерения	Независимые переменные				Зависимая переменная
	Xji	Xj2		xJlj

Многомерные уравнения регрессии ассоциируются с многомерными многосвязными объектами, модель которого представлена на рисунке 1. Построение соотношения вида (12) в

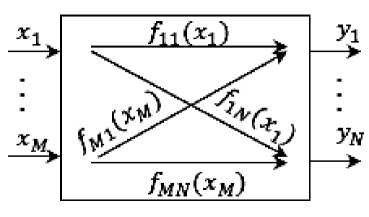
Рисунок 1 – Модель многомерного многосвязного объекта

зависимости от формы представления компонент вектора независимой переменной и зависимой переменной

(измерительные данные, экспертные оценки) сводится к использованию одного из преобразований (6), (8), (10) для построения одномерных законов распределения случайных величин с последующей оценкой непараметрических функциональных зависимостей на основе (2).

Наличие одномерных функциональных зависимостей у j = f t j (X j) позволяет свести формирование таблицы 1 к последовательной реализации следующих шагов.

Шаг 1. Посредством датчиков равномерно распре- деленных случайных чисел хt Е [0,1] методом обратных преобразований [11] генерируются независимые q (q = 1; Q) значения случайных величин fj9), соответствующие оценкам законов распределения F (Xj )

• (13)                         $) = F ^-1 (xjt), i = 1?M .

Шаг 2. По значениям f(9), используя построенные одномерные параметрические зави симости ftj (Xj) рассчитываются значения у j по правилам

• (14)                       yf= ^ f t (fj,”) .

Шаг 3. Значения {f ⁽⁹\ у j ^(q) } заносятся в виде строки в таблицу 1.

В последующем на основе сформированной таблицы, используя известные методы мно- гомерного регрессионного анализа, строится параметрическая многомерная регрессионная зависимость.

Пример. Допустим, имеется двумерный многосвязный объект. Первому входному пара- метру ставится в соответствие экспертная оценка вида хг Е [0; 8]. Второму входному параметру ставится в соответствие выборка случайных величин, которая может быть аппрокси- мирована нормальным законом распределения М(4,1). Зависимой переменной у 1 ставится в соответствие выборка случайных величин, которая может быть аппроксимирована нормаль- ным законом распределения V(8,2). Зависимой переменной у2 ставится в соответствие экс пертная оценка вида {2, [0, го)}.

Зависимые и независимые переменные связываются соотношениями

pl = f 1 1⁽ X 1 ) +f 21 (X 2 ) l^y 2 = ^f2 2^(х2 ) + ^f12^(х1 )

С учётом формы представления экспертной оценки, соответствующей , в качестве F₁ (х) используется равномерный закон распределения F(xf) = 1^ ¹ dr. С учётом, что F(y_T ) описывается нормальным законом распределения, непараметрическая оценка в соответствии с (2) приобретает вид, представленный на рисунке 2.

С учётом формы представления экспертной оценки, соответствующей , в соответствии с (8) в качестве F(y2) используется показательный закон распределения с параметром

X = 0,5. Учитывая, что закон распределения F(%₂) является N (4,1), непараметрическая оценка Д ₂(%₂) в соответствии с (2) приобретает вид, представленный на рисунке 3.

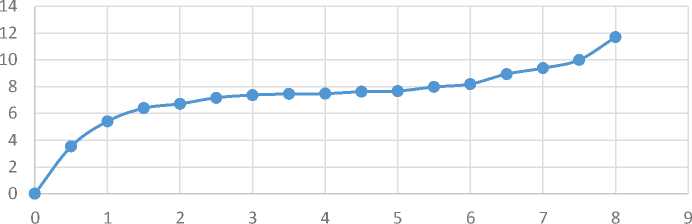
Рисунок 2 - Непараметрическая оценка ^ 1(хх)

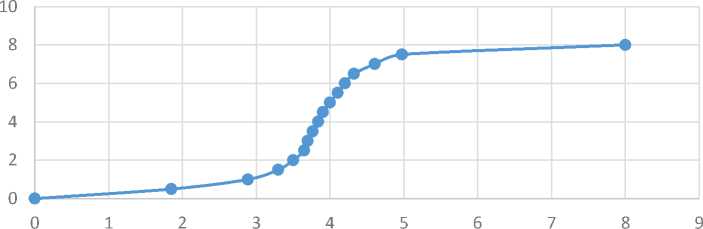
Рисунок 3 - Непараметрическая оценка f2 2(х2)

С учётом того, что закон распределения FC^y) является равномерным, а F(y₂) - показательным, использование (2) позволяет получить оценку Д ₂(%₁), представленную на рисунке 4. Учитывая, что F(y₂) имеют одинаковый тип, использование (2) приводит к представлению Д_{2 1}(%₂ ) в виде линейной зависимости (рисунок 5).

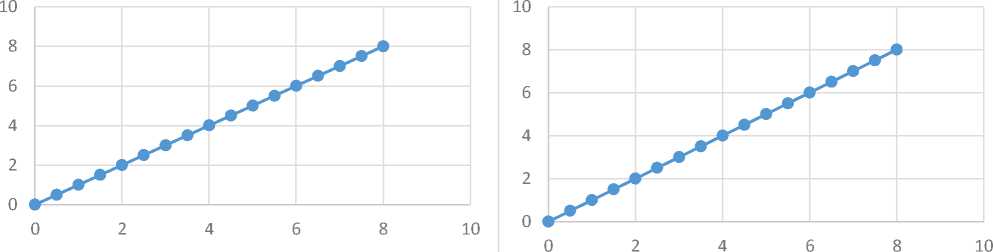
Рисунок 4 - Непараметрическая оценка ^2 (х1)       Рисунок 5 - Непараметрическая оценка f2 1(х2 )

Используя описанный трёхшаговый алгоритм, сформированная таблица, содержащая значения независимых x 1 и x 2 и зависимых и переменных. Фрагмент её представлен в таблице 2. При построении таблицы значение Q принималось Q= 1000 .

На основе этой таблицы с использованием пакета Matlab построены двумерные регрессионные зависимости, представленные на рисунках 6 и 7.

Описанный подход может быть перенесён на случай, когда N в соотношении (12) больше двух.

Таблица 2 – Фрагмент таблицы совместно наблюдаемых значений независимых и зависимых переменных

Номер измерения	Xi	X2	У1	у2
1	0	0	0	0
2	0,5	1,84	3,52	0,5
3	1	2,88	5,40	1
4	1,5	3,29	6,38	1,5

Заключение

Предложен подход к построению многомерных регрессионных зависимостей для случая, когда исходные данные, соответствующие разным компонентам векторов независимой и зависимой переменных, представляются либо в виде результатов измерений, либо в виде разных по форме экспертных оценок. Основу метода составляет преобразование исходных данных, представляемых в разной форме, к виду закона распределения непрерывной случайной величины. Это делает возможным построение совокупности одномерных монотонных на интервале непараметрических регрессионных зависимостей на основе попарного исследования законов распределения независимых и зависимых случайных величин. Полученные регрессионные зависимости служат основой формирования таблицы совместно наблюдаемых значений независимых и зависимых случайных величин, что делает возможным строить многомерные регрессионные зависимости известными методами. Ограничением подхода является, во-первых, необходимость априорного логического обоснования наличия связи между независимыми и зависимыми переменными. Во-вторых, метод ориентирован на построение лишь монотонных на интервале регрессионных зависимостей.

Работа поддержана грантом 19-08-00177 Методологические, теоретические и модельные основы управления функциональной безопасностью аппаратно-программных комплексов в составе распределенных сложных технических систем.