Построение негомогенной конечно-элементной модели по данным компьютерной томографии

Костная ткань обладает неравномерными механическими свойствами, что является следствием ее адаптационных свойств [3, 8, 19‒21]. Снижение физической активности [24, 34], физиологические [11, 12] или возрастные особенности могут приводить к локальной потере прочности костных органов. В клинической практике это может обусловливать расхождение между реальным поведением органа и ожидаемым (моделируемым) результатом оперативного вмешательства. В ортопедии и травматологии множество исследований направлены на улучшение методик оперативного вмешательства [15, 17, 18], оптимизации используемых стержневых аппаратов [2, 4, 5, 7‒10], но на практике, ввиду сложности прогнозирования поведения материала костной ткани [27, 30‒32], многие решения о тактике операции приходится принимать хирургу на месте. В связи с этим актуальной задачей становится оценка механических свойств органа не в интегральном, но в распределенном смысле. Современные подходы к численному моделированию позволяют решать задачи для сложных областей [6, 13, 14, 16, 23, 25, 36], наряду с развитием компьютерной томографии, благодаря которой можно судить о внутреннем строении органа, задача индивидуализации при моделировании органов из костной ткани может предоставить полезную информацию в предоперационный период.

Целью нашего исследования является построение конечно-элементной модели, позволяющей учитывать особенности распределения механических свойств (модуль Юнга и предел прочности) по данным компьютерной томографии, и определение ее напряженно-деформируемого состояния.

Материалы и методы

Постановка задачи

Принятые допущения: при построении модели авторы предполагают, что материал изотропный и негомогенный. Более того, исходя из предположения наличия связи между физической плотностью и механическими характеристиками, будем использовать оптическую плотность для расчета модуля Юнга и предельных напряжений.

Математическая модель

Расчетная область включает в себя некоторое негомогенное тело. Обозначим его за V, а за ∂V ‒ границу этого множества (свободную поверхность). Механическое поведение системы, занимающей область V в R3 с границей ∂V, в рамках линейной теории упругости описывается следующей системой уравнений:

V-d = 0, Vx е V,(1)

s = -(Vи + (Vи)T), Vx е V,(2)

ст = ф(x) • E: s , Vx е V,(3)

где V= Vид V, ст - тензор напряжений; s - тензор упругой деформации; и - вектор перемещений; E - тензор упругих свойств, ф(x) - некоторая функция, определяющая негомогенность среды.

Более того, предположим, что допустимые напряжения также зависят от пространственной координаты:

[о] = [о( x )] ,   V x g V ° .                               (4)

Тогда для оценки напряженно-деформируемого тела введем коэффициент запаса, определяемый по формуле

k ( ^x ) = O V^ x ) , V x g V ° ,                        (5)

[o( x )]

где g_vm( x ) - напряжения по Мизесу в заданной точке. В этом случае ключевую роль будут играть зоны, где введённый выше коэффициент (5) превышает единицу.

Для построения моделей органов из костной ткани предлагается использовать данные компьютерной томографии, в этом случае для каждой точки x g V ° можно сопоставить значение компьютерной томографии CT ( x ) . Для удобства использования таких данных их принято нормировать (шкала Хаунсфилда):

1П^{3 СТ ( x} )^— CT                      ^л

# СТ ⁽ x ) = 10              ,                         (6)

CTw — CTa где CT , CT ‒ линейные коэффициенты ослабления для воды и воздуха соответственно.

Из широкого спектра исследований [1, 3, 22, 26, 29, 33] известно, что существует связь между числами Хаунсфилда и оптической плотностью, упругими константами, предельными напряжениями. В общем виде эти зависимости можно записать так [26, 29, 33]:

P = ap + bp- #CT,(7)

E = «вPbE ,(8)

• [о] = aoPbo,(9)

здесь коэффициенты a и b с соответствующими индексами определяются из эксперимента и могут варьироваться в зависимости от вида костной ткани или органа.

Численное решение задачи

Численная реализация проводилась на основе метода конечных элементов. Основная идея заключается в построении взаимосвязи между конечно-элементной сеткой и данными компьютерной томографии. Для этого необходимо на дискретизированном множестве, которое представляет собой набор данных узлов (их координаты) и элементов (номера узлов, образующие элемент), определить коэффициенты ослабления в узлах.

Nd i = Nd ( x ), V x G V ° D , i = 1, N node ,                     (10)

El p = El ( N,N j , N k ,N , ), p = 1, N ^,                   (11)

где V °_D - конечно-элементная дискретизация объема V ° ; Ned, Nd ( x ) - номер узла и его координаты; El p , El - номер элемента и образующие его номера узлов, N_node^ N_eiem - количество узлов и элементов соответственно.

Далее проводится осреднение механических характеристик для каждого элемента, что позволяет, находясь в упругой постановке, использовать классические конечные элементы. Для определения коэффициентов запаса (5) создается массив допустимых напряжений, по размерности совпадающий с количеством узлов в сетке. Для обработки данных томографии был использован программный продукт Avizo , для конечно-элементного моделирования ‒ ANSYS .

Для конечно-элементного моделирования напряженно-деформированного состояния органа применялся четырехузловой конечный элемент с линейной аппроксимацией solid 186. Для осреднения коэффициентов ослабления в элементе использовалось среднее арифметическое, что накладывает условия на форму конечного элемента (равномерность трех линейных размеров).

Выражения (7)‒(9) удобно выразить сразу через числа Хаунсфилда:

E = а_Е • # CT^b,                                (12)

• [а] = а_ст • # CT^b .                                  (13)

Используемые значения коэффициентов в выражениях (12)‒(13) приведены в табл. 1 [26, 29, 33, 28].

Таблица 1

Значения параметров

Коэффициент	a	b
Модуль Юнга E	46·103	2
Предельное напряжение σ	60	1,82

В случае конечно-элементной модели соотношения для определения коэффициента запаса (5) можно переписать в виде k (Nd ) = aVM (Ndi), i = 1, V , .                        (14)

^{V i?}     [а( Nd )] ,       , node                              (   )

Анализ напряженно-деформированного состояния органа в этом случае будем проводить по данным коэффициента запаса (14).

Модельная задача

Для расчетов была рассмотрена бедренная кость (см. рис. 1, а ). Изучались следующие задачи: 1) одноосное сжатие, 2) изгиб и 3) совместный изгиб со сжатием. В табл. 2 приведены величины сил. Для оценки значимости предлагаемого подхода были рассмотрены две модели: первая негомогенная – напряженно-деформированное состояние определяется по описанной методике, вторая гомогенная – задача напряженно-деформированного состояния решается для некоторого осреднения механических свойств по всему объему: E = 32 ГПа, σ = 48 МПа.

Величины сил

Таблица 2

Расчетный случай	F 1 , Н	F 2 , Н
1	20	0
2	0	200
3	20	200

Образец бедренной кости подвергался сканированию на компьютерном томографе Vatech PaX-I 3 D . Данные обрабатывались в программном комплексе Avizo . Порог экстерьера определялся по методу Отсу, методика обработки подробней изложена в работе [35]. Далее для множества точек, относящегося к органу, строилась поверхностная сетка и после этого объемная сетка. Для удовлетворения равномерности размеров элементов строилась довольно мелкая сетка (порядка 14·10⁴ узлов и 7·10⁵ элементов).

Данные о сетке и значениях чисел Хаунсфилда в узлах экспортировались в файл, который загружался в программный продукт ANSYS . Там проводилось распределение осредненных (по элементу) механических характеристик, накладывались кинематические и статические граничные условия, производились решение

а

б

в

Рис. 1. Рассматриваемый образец: а – томография бедренной кости; б – диафизарный участок бедренной кости; в – расчетная схема и расчет коэффициента запаса (14). В расчетах рассматривался диафизарный участок бедренной кости (см. рис. 1, б). На рис. 1, в приведена схема граничных условий: к поперечному сечению AD прикладывалась нагружающая сила, на поперечном сечении BC фиксировались все перемещения узлов, величины сил приведены в табл. 2. Далее в программном комплексе ANSYS решалась задача напряженно-деформированного состояния и определялись коэффициенты запаса по формуле (12).

Результаты и обсуждение

Для построенной конечно-элементной сетки производилась ее загрузка в программный продукт ANSYS . Каждому элементу назначался параметр, определяющий значение модуля Юнга и предела прочности согласно (12), (13) (на рис. 2 приведена сетка с цветовой диаграммой, указывающей распределение модуля Юнга и предельных напряжений по объему). На рис. 2 можно видеть, что наибольшей жесткостью и прочностью обладает кортикальная кость (красные области на рисунке). Стоит прокомментировать синие вкрапления на внутренней поверхности кости, которым соответствуют малые модуль Юнга и предел прочности, это вызвано наличием пор, которые при сканировании ослабляют интегральные значения коэффициента ослабления в малой области.

После получения решения анализировались поля распределений напряжений по Мизесу и коэффициента запаса, рассчитанного по соотношению (14). На ряду с негомогенной задачей рассматривалась связанная гомогенная задача (обладающая той же геометрией, теми же граничными условиями, но с осреднёнными по всему объему механическими характеристиками).

σ    16     20      24     28     33     38     43     48     54    60   МПа

E   0,80     2       4       7      10      14      19     24      30     36   ГПа

Рис. 2. Распределение механических параметров по конечно-элементной модели: модуля Юнга и предельных напряжений

Расчетный случай 1

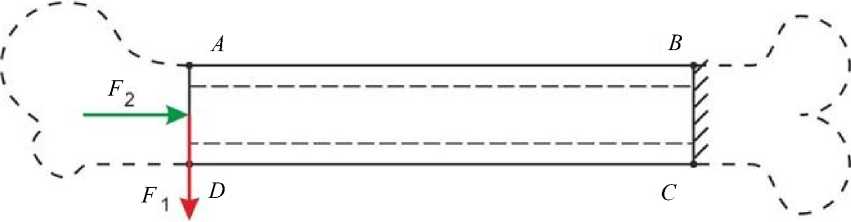
Для случая сжатия негомогенного образца локализация максимальных напряжений по Мизесу происходила в середине кортикала кости на расстоянии примерно трети длины образца от заделки (см. рис. 3, а ). Для гомогенного образца локализация максимальных напряжений по Мизесу происходила на внешней поверхности кортикала и незначительно перемещалась в продольном направлении к нагруженному торцу (см. рис. 4, а ). Численные значения максимальных напряжений в обоих случаях отличались незначительно: 36 и 37 МПа для негомогенного и гомогенного образцов соответственно. Картины полей коэффициента запаса отличались существенно.

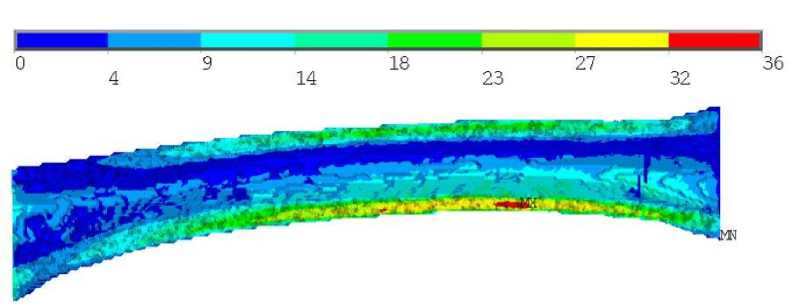
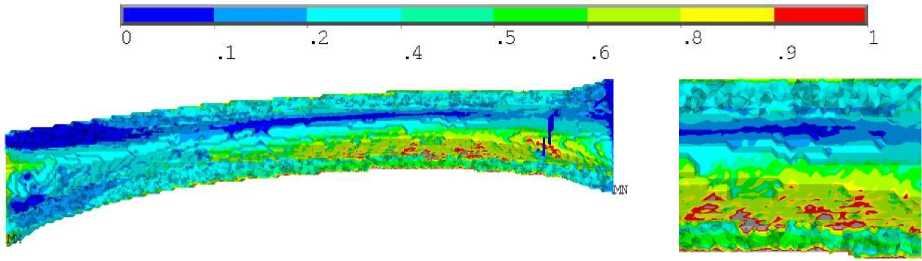
Рис. 3. Результаты для первого расчетного случая негомогенного образца: а – распределение напряжений по Мизесу, МПа; б , в ‒ распределение коэффициента запаса

а

б                                               в

Рис. 4. Результаты для первого расчетного случая гомогенного образца: а – распределение напряжений по Мизесу, МПа; б , в ‒ распределение коэффициента запаса

В случае негомогенного образца коэффициент запаса превышал единицу на внешней и внутренней поверхностях кости, в области локализации максимальных напряжений по Мизесу, при этом эта область протяжённая: почти половина образца (рис. 3, б , в ), наибольшее значение коэффициента запаса в этом случае составило 1,38. Для гомогенного образца наибольшее значение коэффициента запаса достигалось в той же области, где локализовались максимальные напряжения по Мизесу, наибольшее значение коэффициента запаса в этом случае составило 0,89 (см. рис. 4, б , в ). То есть согласно негомогенной модели образец будет претерпевать разрушение, в то время как согласно гомогенной постановке критических значений напряжения не достигают. Разница в коэффициентах запаса составила 55%.

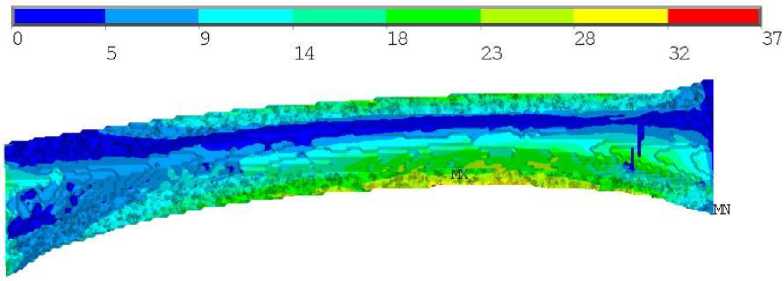
Расчетный случай 2

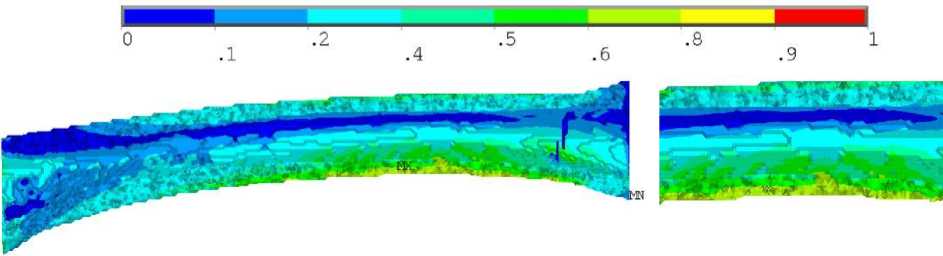
Для случая изгиба негомогенного образца локализация максимальных напряжений по Мизесу происходила в середине кортикала кости на малом удалении от заделки (рис. 5, а ). Для гомогенного образца локализация максимальных напряжений по Мизесу происходила на внешней поверхности кортикала и примерно на таком же расстоянии от заделки, как и в негомогенном случае (рис. 6, а ). Численные значения максимальных напряжений в обоих случаях отличались незначительно: 24 и 23 МПа для негомогенного и гомогенного образцов соответственно. Различия картин распределения коэффициента запаса схожи с первым расчетным случаем. В случае негомогенного образца коэффициент запаса был близок к критическому значению (единице) на внешней и внутренней поверхностях кости, в области локализации максимальных напряжений по Мизесу, при этом эта область значительна (см. рис. 5, б , в ), наибольшее значение коэффициента запаса в этом случае составило 0,95. Для гомогенного образца наибольшее значение коэффициента запаса достигалось в той же области, где и локализовались максимальные напряжения по Мизесу, наибольшее значение коэффициента запаса в этом случае составило 0,58 (см. рис. 6, б , в ). То есть согласно негомогенной модели образец будет близок к разрушению, в то время как согласно гомогенной постановке критических значений напряжения не достигают с достаточным запасом. Разница в коэффициентах запаса составила 63%.

Расчетный случай 3

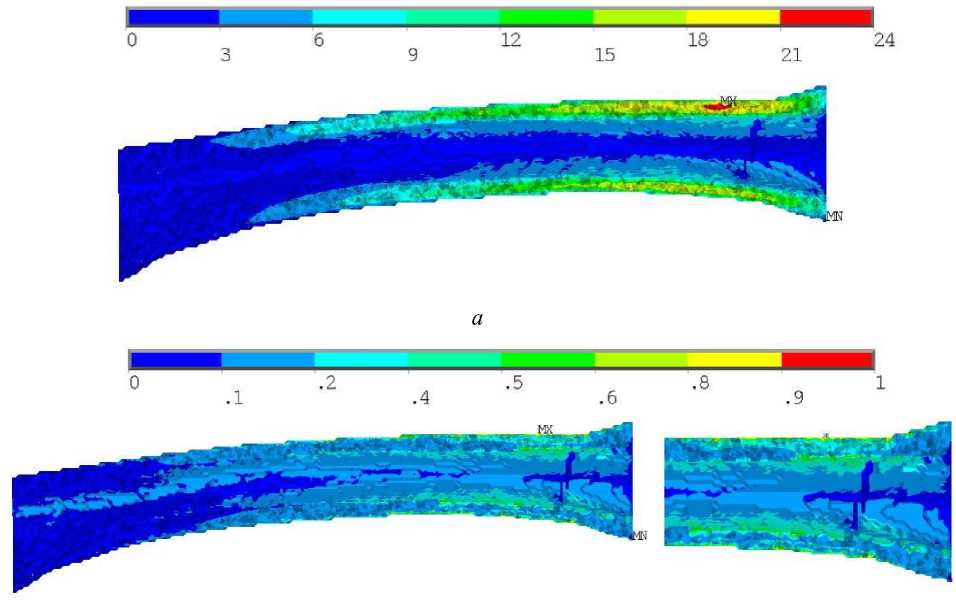
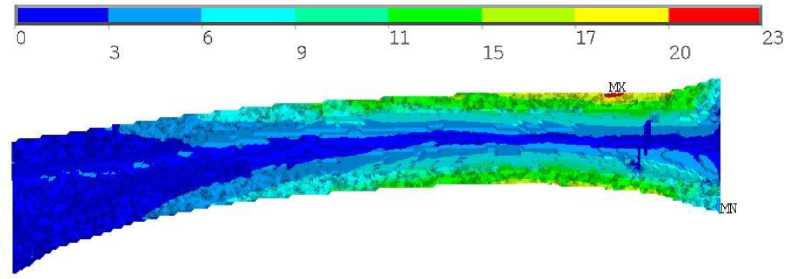
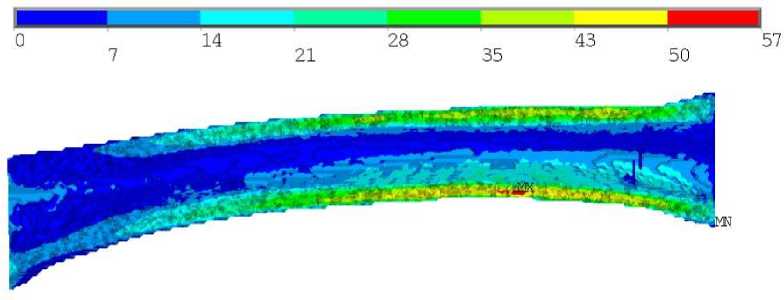
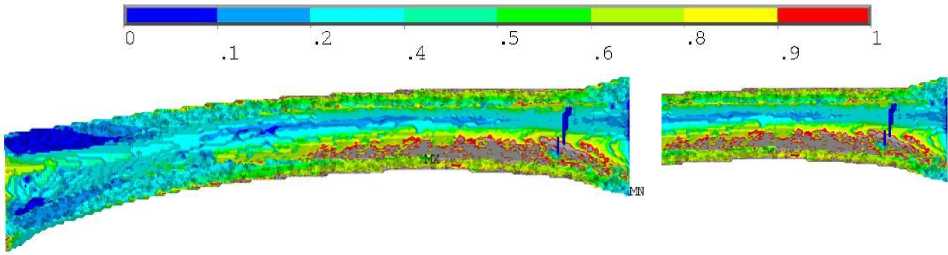
Для совместного случая нагружения негомогенного образца локализация максимальных напряжений по Мизесу происходила в середине кортикала кости на расстоянии примерно трети длины образца от заделки (рис. 7, а ). Для гомогенного образца локализация максимальных напряжений по Мизесу происходила на внешней поверхности кортикала и незначительно перемещалась в продольном направлении к нагруженному торцу (см. рис. 8, а ). Численные значения максимальных напряжений в обоих случаях отличались незначительно: 57 и 53 МПа для негомогенного и гомогенного образцов соответственно. Картины полей коэффициента запаса отличались существенно. В случае негомогенного образца коэффициент запаса превышал единицу на внешней и внутренней поверхностях кости, в области локализации максимальных напряжений по Мизесу, при этом эта область протяжённая: почти половина образца и распространяется по окружному направлению (рис. 7, б , в ), наибольшее значение коэффициента запаса в этом случае составило 2,33.

б

в

Рис. 5. Результаты для второго расчетного случая негомогенного образца: а – распределение напряжений по Мизесу, МПа; б , в ‒ распределение коэффициента запаса

а

б

в

Рис. 6. Результаты для второго расчетного случая гомогенного образца: а – распределение напряжений по Мизесу, МПа; б , в ‒ распределение коэффициента запаса

а

б                                             в

Рис. 7. Результаты для третьего расчетного случая негомогенного образца: а – распределение напряжений по Мизесу, МПа; б , в ‒ распределение коэффициента запаса

а

б

в

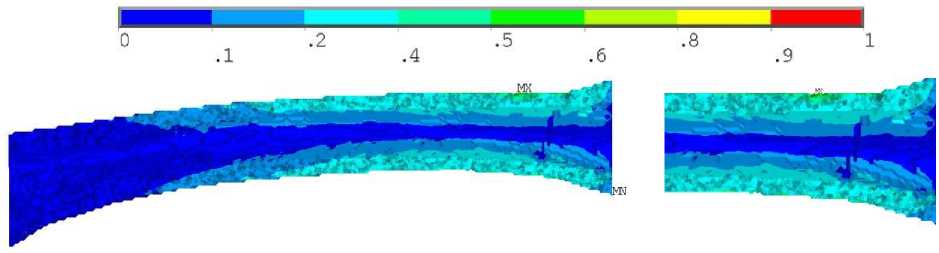
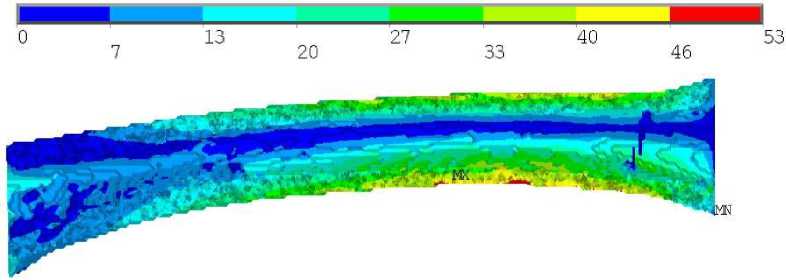
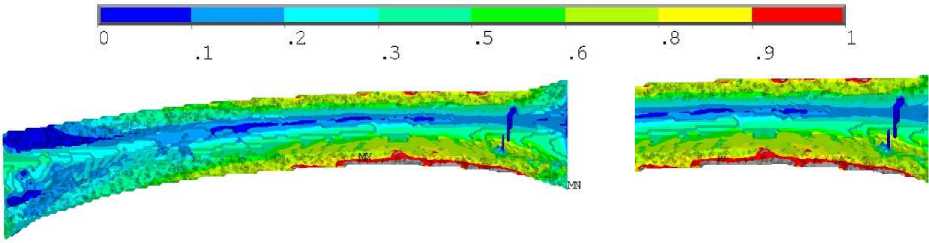
Рис. 8. Результаты для третьего расчетного случая гомогенного образца: а – распределение напряжений по Мизесу, МПа; б , в ‒ распределение коэффициента запаса

Для гомогенного образца наибольшее значение коэффициента запаса достигалось в той же области, где и локализовались максимальные напряжения по Мизесу – на внешней поверхности кортикала, наибольшее значение коэффициента запаса в этом случае составило 1,28 (рис. 8, б , в ). Разница в коэффициентах запаса ‒ 82%. То есть при совместном нагружении образец будет разрушаться при много меньших силах, согласно расчету негомогенной модели, чем те, которые рассчитываются при гомогенной модели. Эти примеры иллюстрируют необходимость учета распределения механических свойств костного органа при моделировании напряженно-деформированного состояния. Качественным образом изменяются картины распределения коэффициентов запаса, значительно изменяются их количественные значения. Приведенная методика позволяют моделировать механическое поведение костных органов с учетом индивидуализации не только геометрии органа, но и его механических свойств.

Выводы

• 1.    В работе приведена методика для построения конечно-элементной негомогенной модели органа из костной ткани по данным компьютерной томографии.

• 2.    Численные результаты модельных задачах иллюстрируют значимые различия в результатах напряженно-деформированного состояния органа и позволяют судить о локальной прочности костной ткани.

• 3.    При моделировании принимались следующие допущения: негомогенный материал изотропный, существует связь между физической плотностью и механическими характеристиками, что позволяет использовать оптическую плотность для расчета модуля Юнга и предельных напряжений.

• 4.    Применение описанной методики позволяет на основании анализа результатов коэффициентов запаса  делать  заключение о напряженно-деформированном

• 5.    Предлагаемая модель может быть расширена с учетом ортотропности материала.

состоянии объекта при различных внешних нагрузках.

Благодарности

Работа выполнена при финансовой поддержке гранта Президента Российской Федерации для государственной поддержки молодых ученых МК-1717.2018.1.

Авторы выражают отдельную благодарность сети независимых диагностических центров «Пикассо».