Построение оптимальной стратегии производственно-экономической деятельности нефтяной компании в Российской Федерации

В современных экономических условиях деятельность производственных компаний представляет собой динамичную систему финансовых, материальных и информационных потоков, в рамках которых формируется конечный продукт. Он распределяется на вложения в производство, расходы на оплату труда и т.д. Распределение должно быть оптимальным, исходя их критериев повышения эффективности деятельности компании.

Построение стратегий оптимального распределения средств относится к классу задач управления. Особое место задачи управления занимают при планировании развития крупномасштабных предприятий, имеющих важное народнохозяйственное значение [1].

В условиях меняющегося окружающего мира важным конкурентным преимуществом при стратегическом планировании развития компании является инвестирование в повышение эффективности труда.

В 2017 году Правительством РФ была разработана программа [2] по созданию условий для перехода страны к цифровой экономике. В рамках программы предусматривается трансформация рынка труда: он должен опираться на требования цифровой экономики [3]. В этих условиях актуальна задача наращения качественного потенциала трудовых ресурсов.

В данной работе рассмотрена деятельность публичного акционерного общества «Нефтяная компания «Роснефть» (ПАО «НК «Роснефть»). Для решения задачи оптимального планирования ее производственно-экономической деятельности в качестве исходной математической модели рассмотрена модель, представленная в работе [4]. Отличительной особенностью постановки задачи является включение в нее фактора эффективного объема трудовых ресурсов как ведущего фактора, участвующего в создании конечного продукта.

Гипотеза, принятая в модели: эффективный объем трудовых ресурсов состоит из количественной и качественной составляющих. Количественная есть численность трудовых ресурсов. Качественная формируется из расчета эффективности труда работников.

В настоящее время не существует единой стройной теории оценки эффективности труда. Подробный анализ этой проблемы представлен в [5], где отмечено, что существует несколько обобщенных точек зрения. Одним из подходов к оценке эффективности труда является критерий заработной платы.

Проблема соотношения темпов роста производительности труда и заработной является предметом научных исследований [6]. Рост производительности труда должен сопровождаться пропорциональным ростом заработной платы. Это приводит к повышению показателей экономической эффективности.

Производимый (в денежном измерении) продукт распределяется на расходуемую потребляемую часть (прибыль, налоговые выплаты, себестоимость за вычетом оплаты труда и прочие расходы), инвестиции в поддержание и расширение производственного капитала и инвестиции, направленные на развитие социальнообразовательного потенциала компании. Этот потенциал формирует эффективный объем трудовых ресурсов.

Математический аппарат, применяемый для решения задач оптимального управления, включает принцип максимума Л.С. Понтрягина и принцип оптимальности Р. Беллмана [7]. В рамках этих подходов сформулировано необходимое условие оптимальности в терминах существования двойственных переменных, удовлетворяющих определенным соотношениям, в которых присутствуют переменные управления. Полное аналитическое решение модели оптимального управления с использованием принципа Беллмана представлено в работах [8, 9]. Для построения стратегии оптимального планирования производственно-экономической деятельности ПАО «НК «Роснефть» будем использовать принцип Понтрягина.

Постановка задачи

• 1.    При моделировании производственно-экономической деятельности компании будем рассматривать показатели: валовый объем производства Y , производственный капитал K , инвестиции в производственный капитал I , эффективный объем трудовых ресурсов Z , инвестиции на развитие социально-образовательного потенциала компании E , и расходуемая потребляемая часть C , которая включает в себя чистую прибыль, налоговые выплаты, себестоимость за вычетом оплаты труда и прочие расходы.

• 2.    Эффективный объем трудовых ресурсов ^{Z ( t} ) в момент времени t зависит от средней эффективности одного работника z ^{( t} ) и численности работников ^L ( t ) : Z ( t ) = L ( t ) z (t ) .

• 3.    Фазовыми переменными модели являются производственный капитал K и эффективность одного работника z , их динамика описывается уравнениями: K = I ^- П k K , _и ^z = М ^EI^{L )-} n z ^Z _; П к и ^{П z} - коэффициенты выбытия факторов.

• 4.    Объем производства определяется производственной функцией Y = F ( K , Z ) ;     она     линейно-однородна,     т.е.

• 5.    Каждый год происходит распределение      произведенного      продукта

F(K, Z) = LF(K/L, Z/L) = LF(к, z)

.

к = K/L   - _ / и „    „ „

Здесь      ' и z ZIL удельные ве личины производственного капитала и эффективного объема трудовых ресурсов.

Y = C + I + E на части: инвестиции I , E в производственные факторы K , Z соответственно и расходуемую потребляемую часть C , которая включает в себя чистую прибыль P , налоговые выплаты N , себестоимость за вычетом оплаты труда и прочие расходы (рис. 1).

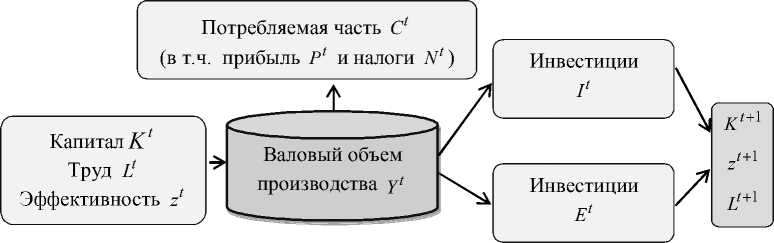
Рис. 1. Схема цикла производственно-экономической деятельности компании

, Vt g[0, T]

6.         , должен сохраняться не-

C которыи минимальный уровень mn , зна-

~k=nk+ (LL )

,

z = szf(k , z )-n zz

.

чит,

c = c + C ■

C C + Cmin

.

Тогда

Y := Y — Cmin, F(K,Z) := F(K,Z) — Cmin и ограничения на факторы производства 0 < Cmm < F (K, Z).

;

Y = C +1 + E > 0, C,I, E > 0.

7. Управление осуществляется согласно

s =(sr,s,,s,)

вектору       c k z , где норма по- sr = C/Y  s, = I/Y требления c       , k       – норма

Начальное и конечное состояния системы

k(t0) = k0, z(t0) = z0; k(tT) = kT, z(tT) = ZT kT = k (tT), zT = z (tT)

. Причем T      ^v T , T        T ⁷, где

*     *

k , z

– значения переменных на траектории сбалансированного развития.

10. Критерием оптимальности задачи является удельное дисконтированное накопленное за весь период планирования

инвестиций в K , s ^z стиций в E , причем

= E/Y

– норма инве- sr + sk + s, < 1

ckz

.

8. Из общего числа работающих в компании ^{L ( t} ) будем выделять число работников, находящихся на больничном. Тогда ^{L ( t} ) - работники, присутствующие на рабочем месте и участвующие в создании конечного продукта в момент t . Доля работающих в момент t в общей численности ^X = ^LE е ( 0,1 ] , т.к. 0 < L ( t ) < L ( t )

⁰ , T                        потребление:

^C r = T ^{( S}c^{f (} k , z ^{)X + c} min e "⁵⁽ t — t ⁰ ) ^dt ^ max s eQ t 0

. Множество допустимых управлений

Q = j(Sl )=(Sk, Sz ) : Sl e[0,1] S sl = 1 - sc ।

.

11. Информационный паспорт задачи

f^, n, f, cm, n, X, 5, T}  8

имеет вид 1,  2,  , mm ,  ,  ,   , О

–

.

9. Уравнения для фазовых переменных

с учетом

s c = C/Y    S k = I/Y

,

,

s, = E/Y                       „ z        и вследствие перехода от абсолютных    величин    к    удельным

k = K/L, y = Y/L, cmin = C,„/P ,

yy = Y/L = F (K, Z)/L = f (k ,z) = f (k, z) - c„n / X, примут вид:    k = skf(k, z)  П kk,

коэффициент дисконтирования, T – период планирования.

Сформулированная задача является задачей оптимального управления производственно-экономической    деятельностью компании с учетом эффективного объема трудовых ресурсов.

Алгоритм решения задачи

Будем говорить о двух частях оптимальной траектории. Первый участок представляет собой переходный период до момента достижения объективной траектории сбалансированного развития, второй участок – движение по этой траектории.

Обозначим вектор фазовых переменных x = ^{( k} , ^z ) , вектор двойственных перемен-

ш = (ш,,ш J ных        k z , вектор переменных

s = (s„, s,., s.) управления      c k z

.

В изложении игнорируем факт наличия фазовых ограничений. Наложенное выше

0 < с < Xf условие      min J обеспечивает при сутствие системы в той области фазовой

f (k, z )> 0 г плоскости, где            . Гамильтониан

задачи H(ш, s, x, t):

H = [(1 — sk — sz )f(k, z)X + cmin e t + +Шk [skf(k, z) — ~kk] + Шz [szf(k, z) - Пzz 1 (1)

Необходимые условия принципа максимума [7] для задачи (1-11):

• 1.    При каждом фиксированном t ^{g [ 0, T 1} :

• 2.

2. Двойственные переменные ^{k z} должны удовлетворять системе

sk (t) = argmax H (ш, s, x, t),   sz (t) = argmax H (ш, s, x, t )

⁽ s k , s z ) en                                        ( s k , s z ) efi

Vt , V,

'■'k =-(dHldk) шz =-(dH/dz),

фазовые переменные ^k , z

должны удовлетворять системе уравнений

k; = dH/ 5ш^, z = dH/ 5ш2

с краевыми условиями

k(0)=k0, z(0)=zo; k(T)=kT, z(T)=zr

Вводя замену для вектора двойственных переменных 8- 1                      8- 1

k ^{_ ш} k e  , z ^{_ ш} z e , преобразуем (1) к виду:

п = (п k, П z )

н(П s, x, t ) = [(1 - sk - sz ) f (k, z)X + cmin ]e"8t +

+ Пke"5t [skf (k, z) — ~kk 1 + Пze"5t [szf (k, z) - Пzz1

Условие (2) применительно к (6) запишется в виде:

argmax sk(nk -X)+sz(nz -X) s gQ

откуда определим управления

s k ^{( t} )_и s z ^{( t} )

.

Система (3) с учетом замены для двойственных переменных:

< ; k =(8 + ~ k )n k -[(1 — sk — sz )X + sk П k + sz П z ]fk (k, z ) , Пz =(8 + n z )nz -[(1 — sk — sz )X + sk Пk + sz Пz ]fz (k, z)

а уравнения (4) примут вид:

k = skf (k’ z )-П kk’ z = szf(k’ z )-П zz •

Траектория сбалансированного развития определяется из условий:

ⁿ k =ⁿ z =^k ,   ^П k =ⁿ z = ^k ’

Подставив (10) в (8), (9), найдем параметры k *

*     *

* s s z , k , z сбалансированного разви- тия:

/ (i*   *\                          fill*   *^

fk(k,z )=s + nk —WM’fz(k,z )=5 + nz -(kA), _ sk =(~ kk *+k^*)/ f(k *, z *), s*=(n zz *+z^ *)/ f(k \ z * )•

Для построения переходного периода используются нестационарные уравнения (8) и (9), которые решаются в обратном времени с использованием метода Эйлера с коррекцией [10]. Исходя из начальных значений ⁰ ’ z ⁰ в ходе решения подбира- *

ется момент времени t , в который оптимальная траектория выходит на траекторию сбалансированного развития. Одновременно при решении восстанавливаются

^{п k ’ ^П z } t и

значения переменных

{s^’s,} k z t . На последнем этапе прямым ходом решается задача оптимального распределения инвестиций.

Результаты решения

Решение задачи управления производственно-экономической деятельностью компании осуществляется на основе имеющихся в свободном доступе статистических данных ПАО «НК «Роснефть» [11], приведенных к сопоставимым ценам 2019 года. Параметры, присутствующие в информационном паспорте задачи, подлежат определению. Они рассчитаны за период 2006-2019 годы в соответствии с алгоритмом идентификации неизвестных параметров [4, 12].

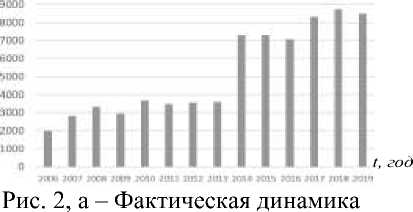
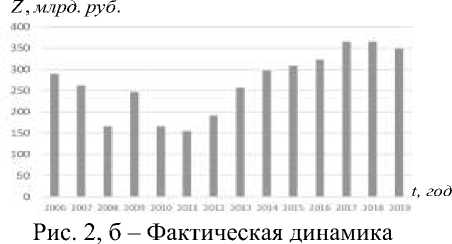
На рис. 2 а, б представлена динамика производственного капитала и эффективного объема трудовых ресурсов, они являются фазовыми переменными модели.

K, млрд • руб •

эффективного объема трудовых ресурсов ПАО «НК «Роснефть» за период 2006- 2019 годы

величины производственного капитала ПАО «НК «Роснефть»

за период 2006- 2019 годы

На рис. 3, а, б – динамика величины валового объема производства и текущей прибыли, которые являются выходными, оптимизмруемыми переменными модели. За период 2006-2019 годы получено, что средний ежегодный темп роста производственного капитала 16,2 %, эффективного объема трудовых ресурсов – 12,8 %, объема производства – 19,7 %, прибыли – 5,1 % (за исключением первого года периода).

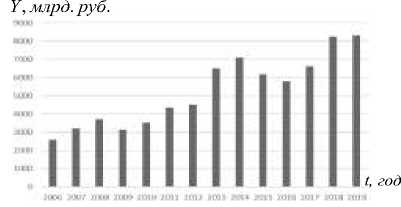
Рис. 3, а – Фактическая динамика валового объема производства ПАО «НК «Роснефть» за период 2006- 2019 годы

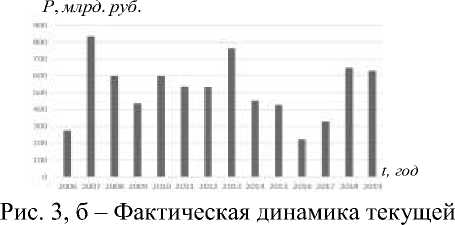
прибыли ПАО «НК «Роснефть»

за период 2006- 2019 годы

Отметим, что текущая деятельность компании эффективна, управление компанией позволяет наращивать ее финансовоэкономические показатели.

На рис. 4, а, б и 5, а, б приведены некоторые результаты решения задачи управления производственно-экономической деятельностью компании ПАО «НК «Роснефть».

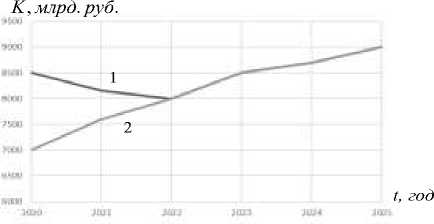
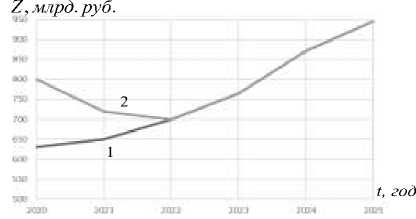
Рис. 4, б – Траектория изменения фазовой координаты ^Z : оптимальная траектория развития ПАО «НК «Роснефть» (1), объективная траектория сбалансированного развития (2)

Рис. 4, а –Траектория изменения фазовой координаты ^K : оптимальная траектория развития ПАО «НК «Роснефть» (1), объективная траектория сбалансированного развития (2)

Параметры деятельности компании достигают значений оптимальной траектории и остаются на ней благодаря математической стратегии управления (7), согласно которой в начальный период следует инвестировать в Z . В это же время уменьшается инвестирование в фазовую переменную K . Таким образом, в первые годы планового периода следует нарастить до- лю инвестиций в развитие социальнообразовательного потенциала компании. Этот процесс происходит до момента достижения траектории сбалансированного развития в 2022 году (рис. 4, а, б). Переходный период в расчетах оказался коротким вследствие того, что мы изучаем компанию, которая придерживается принципов оптимального управления.

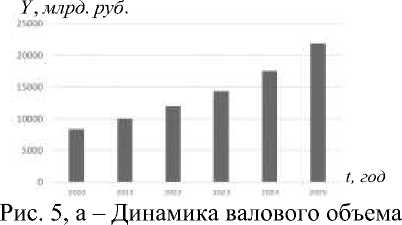
производства ПАО «НК «Роснефть»

при реализации оптимального управления на период 2000- 2025 годы

P , млрд. руб .

t, год

Рис. 5, б – Динамика текущей прибыли ПАО «НК «Роснефть» при реализации оптимального управления на период 2000- 2025 годы

За период 2000-2025 годы реализация оптимальной стратегии управления позволит достичь средних ежегодных темпов роста валового объема производства 21,4 % (по сравнению с имеющимся темпом 19,7 %) и прибыли 5,9 % (по сравнению с темпом 5,1 %) (рис. 5, а, б).

Заключение. В результате решения задачи управления на примере ПАО «НК «Роснефть» получены оптимальные значения финансовых показателей компании. Показано, что выход показателей на сбалансированную траекторию экономического развития при реализации сценария оптимального управления будет осуществлен к 2023 году. При реализации сцена- венный капитал на первом этапе уменьшается. Такая политика открывает возможность повысить эффективность труда в 1,5 раза к 2025 году. Начиная с 2023 года, происходит наращение производственного капитала. Оптимальное распределение инвестиций между производственными фондами и повышением эффективности труда позволяет нарастить валовый объем производства к 2025 году в 2,6 раза. Выявлено, что производственно-экономическая деятельность компании уже демонстрирует применение стратегии, близкой к оптимальной, в связи с чем переход на оптимальную траекторию осуществляется в течение 3-х лет.

рия оптимального управления производст-