Построение полиномиальных решений некоторых задач для уравнения Пуассона

Хорошо известно классическое представление Альманси для полигармонических функций, которое успешно применяется для построения решений модельных задач для бигармонического и полигармонического уравнений (см., например, [1]). В работе [2] уже была сделана попытка построения полиномиальных решений уравнения Пуассона: Au(x) = Q(x) и полигармонического уравнения: A m u(x) = Q(x) (здесь Q(x) — некоторый полином) с помощью формулы Альманси. Найденные решения отличаются от полиномиальных решений дифференциальных уравнений в частных производных общего вида, полученных в [3, 4].

Хорошо известна функция Грина G(x,^) задачи Дирихле в шаре, а поэтому с теоретической точки зрения построение решения такой задачи не представляет интереса. Однако при полиномиальной правой части Q(x) и полиномиальном граничном значении U |_x| =i = P (x) решение u(x) задачи Дирихле оказывается полиномиальным. Для нахождения этого решения при P (x) = 0 необходимо вычислять сингулярный интеграл вида

u(x) =

- — [ G(x,e)Q(€)d€, ω n

iei 2) — элементарное решение уравнения Лапласа [5]. В разделе 2 настоящей работы с помощью исследования свойств представлений Альманси, описанных в леммах 2--4 и теоремах 1, 2. В теореме 4 будет дана формула (22), позволяющая легко вычислять полиномиальное решение u(x), задаваемое формулой (1). Кроме этого, в теореме 6 получена более общая формула (26) для представления полиномиального решения задачи Дирихле уравнения Пуассона с полиномиальными Q(x) и P(x). К сожалению, полученные полиномиальные решения для записи их в обычном виде требуют вычисления степеней оператора Лапласа от некоторых многочленов. Этот недостаток легко устраняется с помощью применения пакета «Mathematica» (см. пример 1).

В разделе 3 рассматривается обобщенная третья краевая задача для уравнения Пуассона (27), когда на границе задается условие P m (d/dv )u |_x| =i = у. А.В. Бицадзе опубликовал в [5] исследования обобщенной задачи Неймана для уравнения Лапласа, когда на границе задается n-я нормальная производная, то есть при P m (t) = t m . В теореме 7 сформулированы условия существования решения обобщенной третьей краевой задачи для уравнения Пуассона. С помощью явного представления гармонических функций в формуле Альманси в теореме 8 получено полиномиальное решение в виде (32) третьей краевой задачи (30) для уравнения Пуассона с полиномиальной правой частью Q(x) и граничными данными P (x).

• II.    Полиномиальное решение однородной задачи Дирихле для уравнения Пуассона

Сначала рассмотрим следующую краевую задачу для уравнения Пуассона в единичном шаре: Q = { x G R n : | x | < 1 } .

Au(x) = Q(x), x G Q;(2)

U|X|=1 = 0,(3)

с полиномиальной правой частью Q(x) и при n >  2. В [6] было доказано, что имеет место представление Альманси, записанное в виде

Q(x) = *) + Е |Z (1 - (k)^/2-1 Vk(NM k-10

где гармонические полиномы v ^ (x), k = 0, 1, ..., определяются формулой

V k (x) = A k Q(x) + XX       j^s f          . a_a n/ ^{2 - 1} A ^k + ^s Q(ax)dQ.

4 ^s S!         (s ^- 1)!

s-1о

Следует отметить, что операторный ряд в формуле (5) является, по сути, конечной суммой, поскольку Q(x) — полином. Поэтому лишь конечное число v ^ (x) в (4) отлично от нуля. Для удобства записи мы сохраним в суммах верхний предел равный ∞ .

Используя представление (4), в работе [2] установлено следующее утверждение.

Теорема 1. Некоторое решение уравнения (2) может быть найдено в виде

2 J^      1т12к

u(x) = f Е _{(2 k )!!} ( ₂ k _{+ 2)!!} ] (1 - a) k а ' ( - ^A) k Q     'a              (6)

где следует считать, что ( - A) k Q(ax) = (( - A) k Q)(ax).

Предположим сначала, что Q(x) = Q m (x ) — однородный полином степени m. В [2] показано, что в этом случае решение (6) может быть записано в виде

∞

v(x) = £(-1)s s-0

| x | ^{2 s +2} A ^s Q m (x)

(2,2) _{s +}i (2m - 2s + n,2) _{s +}i

Здесь (a,b) k = a(a + b)...(a + (k - 1)b ) — обобщенный символ Похгаммера с соглашением (a,b) o = 1. Например, (2,2) k = (2k)!!. Заметим, что выражение (2m - 2s + n,2) s +i = (2m - 2s + n)...(2m + n) не обращается в нуль, поскольку 2s 6 m.

В дальнейших исследованиях нам понадобится одно комбинаторное тождество.

Лемма 1. V a G R + и V m G N имеет место равенство

m

E ( - 1) k ^{- 1}

k -0

(2m - 2k + 2,2) _fc (2m - 2k + a,2) _fc (2,2) _fc (4m - 2k - 2 + a,2) _fc

= 0.

Доказательство этого утверждения легко получается с помощью метода математической индукции.

Рассмотрим уравнение Пуассона со специальной правой частью:

Au = | x | ^{2 m} • P _s (x),x G D,

где P _s (x ) — однородный гармонический полином степени s, m G N n (N o = N U { 0 } ), а D C R n — звездная область с центром в начале координат.

Теорема 2. Решение уравнения (9), записанное в форме (6) или (7), имеет вид

u(x) =

| x | 2 m +2 p s (x)

(2m + 2)(2m + 2s + n)

Доказательство. В силу теоремы

Au = Q(x), x € D, может быть найдено ле (6) вычислим это решение:

1 некоторое решение u(x) уравнения Пуассона в виде (6). Положим Q(x) = | x | ^{2 m} P _s (x). По форму-

∞

u(x) = If E

k =0

( — 1) ^k | x | ^{2 k} (2k)!!(2k + 2)!!

j (1 — a) ^k a ^{k + n/ 2 - 1} A ^k ( | ax | ^{2 m} P s (ax))da.

Рассмотрим выражение A k ( | x | ^{2 m} P _s (x)). Вычислим его при произвольном k € N. Нетрудно подсчитать, что

A( | x 1 ^{2 m} P s (x)) = 2m(2m + 2s + n — 2) | x 1 ^{2 m - 2} P s (x).

Поэтому при 2k 6 2m + s будем иметь

A k ( | x | ^{2 m} P s (x)) = 2m(2m — 2)...(2m — 2k + 2) x

x (2m + 2s + n — 2)(2m + 2s + n — 4)...(2m + 2s + n — 2k) | x | ^{2 m 2 k} P _s (x) = = (2m — 2k + 2,2) _k (2m + 2s + n — 2k,2) k • | x | ^{2 m - 2 k} P _s (x).

Следовательно, можно записать

m

u(x) = f E

k =0

( — 1) ^k | x | ^{2 k} (2k)!!(2k + 2)!!

j (1 — a) ^k a ^{k + n/ 2 - 1} x

x (2m — 2k + 2,2) k (2m + 2s + n — 2k,2) k | ax | ^{2 m 2 k} P _s (ax)da.

И поскольку P _s (ax) = a ^s P _s (x), получим

u(x) = I xr^x x

m x X k=0

( — 1) ^k (2m — 2k + 2,2) _k (2m + 2s + n —

(2k)!!(2k + 2)!!

^k^ J(1 — a) ^k a ^{2 m + s + n/ 2 - k - 1} da.

Вычислим отдельно интеграл в полученном выражении. Имеем j (1 — a)k a2m+s+n/2-k-1da = B(k + 1,2m + s + n/2 — k) =

Г(к + 1) • Г(2т + s + n/2 — k)

k!

Г(2т + s + n/2 + 1)        (2m + s + n/2)...(2m + s + n/2 — k)’ где r(k) — гамма функция Эйлера, а B(m,n) — бета функция Эйлера. Тогда u(x) преобразуется к виду

_ | x | ^{2 m +2} P s (x) X X ( — 1) ^k (2m — 2k + 2,2) _k (2m + 2s + n — 2k,2) k • k!

2 j“ 2 ^k k!(2k + 2)!! • (2m + s + n/2)...(2m + s + n/2 — k)

m

= ixi2m+2p,ot) x k=0

( — 1) ^k (2m — 2k + 2,2) _k (2m + 2s + n — 2k,2) k

(2k + 2)!! • (4m + 2s + n)...(4m + 2s + n — 2k)

m

= |x|2m+2Ps(x) X k=0

( - 1) ^k (2m - 2k + 2,2) k (2m + 2s + n - 2k,2) k

(2,2) k ₊i • (4m + 2s + n - 2k,2) k +1

Пусть a = 2s + n. Покажем, что для m E N o = N U { 0 } верно равенство

m

X

k =0

( - 1) ^k (2m - 2k + 2,2) k (2m + a - 2k,2) k

^(2,2) k +1 ^{- (4m + a - 2k,2)} k +1

(2m + 2)(2m + a)

Легко видеть, что это равенство верно при m = 0. Далее, умножим левую и правую части равенства (10) на (2m + 2)(2m + a). Тогда будем иметь

m

X k=0

( - 1) ^k (2m - 2k + 2,2) _{k +1} (2m + a - 2k,2) _{k +1}

^(2,2) k +1 ^{- (4m + a - 2k,2)} k +1

= 1 ^

m

⇒

-1 + k=0

( - 1) ^k (2m - 2k + 2,2) _k (2m + a - 2k,2) k

^(2,2) k +1 ^{- (4m + a - 2k,2)} k +1

= 0.

Добавим в сумму слагаемое с номером - 1. Тогда получим равенство

m

X

k = - 1

( - 1) ^k (2m - 2k + 2,2) k +1 (2m + a - 2k,2) k +1

^(2,2) k +1 ^{- (4m + a - 2k,2)} k +1

= 0.

Сдвинем индекс суммирования на 1, заменяя k + 1 ^ k. Получим

m +1

X

k =0

( - 1) ^{k - 1} (2m - 2k + 4,2) k (2m + a - 2k + 2,2) k

(2,2) k • (4m + a - 2k + 2,2) k

= 0.

Так как m E N o любое, то вместо m + 1 возьмем m E N:

m

X

k =0

( - 1) ^{k - 1} (2m - 2k + 2,2) k (2m + a - 2k,2) k

(2,2) k • (4m + a - 2k - 2,2) k

= 0.

Мы получили равенство (8). По лемме 1 это равенство справедливо для всех m E N. Так как равенство (11) равносильно равенству (10), то теорема доказана.

Если разложить полином Q _m (x) с помощью формулы Альманси на слагаемые вида | x | 2 ^S R m — 2 s (x), то решение уравнения Av(x) = Q _m (x), задаваемое формулой (7), имеет вид

[ m/ 2] v(x) = ^X s =0

| x | ^{2 s +2} R m - 2 s (x)

(2s + 2)(2m - 2s + n),

где [a] — целая часть числа a, а однородные гармонические полиномы R k (x) определяются формулой Альманси в виде

Q _m (x) = R _m (x) + | x | R _m- 2 (x) + ... + | x | R _m- 2 _s (x).

Какой же вид имеют гармонические полиномы R k (x) в этой формуле?

Лемма 2. Гармонические полиномы R _m- 2 k (x) в разложении однородного полинома Q _m (x) по формуле Альманси (13) имеют вид

R m - 2 k (x) =

2m - 4k + n - 2 X        ( - 1) ^s | x | ^{2 s} A ^{s + k} Q m (x)

(22^       s =0 (2,2) _s (2m - 4k - 2s + n - 2,2) _s + k +1 ^.

Доказательство. Нетрудно заметить, что имеет место следующая связь между полиномом

V k (x) из формулы (5) и полиномом R _m- 2 k (x) из формулы (13):

R m - 2 k (x) =

V k (x) 4 ^k k!(k - 1)

Z (1 - a) ^{k - 1} a ^{m - 2 k + n/ 2 - 1} da = V k (x)^Bk4m - k² - ±n/²) 0

V k (x)               (2m — 4k + n — 2,2)v k (x)

(2,2)k(2m - 4k + n,2)k = (2,2)k(2m — 4k + n — 2,2)k+1, где B(m,n) — бета-функция Эйлера. Отсюда видно, что vo(x) = Rm(x). Воспользуемся формулой (5). Тогда будем иметь

V o (x) = Q m (x) + XX x , Z(1 — a) ^{s - 1} a s ^{+ n/ 2 - 2} A ^s Q m (ax)da =

4ss!(s — 1)! J s-1o

— Q X И__ ^{( A) Qm(x)} Z(1 _ _a)^s-1 ct^{m-s + n/ 2 -2}da

= Qm(x) + 2_,   4s s!(s — 1)! J(1 a)   ada.

s-1

Если воспользоваться свойствами бета B(m,n) и гамма r(s) функций Эйлера, то можно записать

Z(1 _ _a)^s-1 _a ^{m-s + n/ 2 -2}da = B(s m - s + n/2 -   = ^{r(s)r(m — s + n/2 — 1} ₌

j^{(1  a)   a}         d^{a   B(s,}m s⁺ n/2 1)       r(m + n/2 — 1)

o

=______________ ^{(s — 1)!} ______________ =        ^{(s — 1)!}

(m — s + n/2 — 1)...(m + n/2 — 2)   (m — s + n/2 — 1)s, где (m)s = m(m + 1)...(m + s — 1) — символ Похгаммера. Значит:

∞ vo(x) = Qm(x) + s-1

(s — 1)! | x | ^{2 s} ( — A) ^s Q m (x)

(s — 1)!4 s s!(m — s + n/2 — 1) _s

∞ = ^X s -o

_Jx2sHrAsQm^x^_

(2,2) s (2m — 2s + n — 2,2) _s ^.

Если в формуле (5) обозначить v o (x) = v o (x; Q), то получим V k (x) = v o (x; A ^k Q).

Поэтому

∞ vk(x) = 52

s -o

( — 1) ^s | x | ^{2 s} A ^{s + k} Q m (x) (2,2) s (2m — 4k — 2s + n — 2,2) _s ^.

Значит, из (14) выводим:

R _{M =}       2m — 4k + n — 2 X      ( — 1) ^s | x | ^{2 s} A ^{s + k} Q m (x)

m ^{- 2 k (x)}   (2,2) k (2m — 4k + n — 2,2) _{k +1} ^ (2,2) _s (2m — 4k — 2s + n — 2,2) s

2m — 4k + n — 2 X^        ( — 1) ^s | x | ^{2 s} A ^{s + k} Q m (x)

^(2,2) k       _{s -}o ^(2,2) s ^{(2m — 4k — 2s + n — 2,2)} s + k +1

Вернемся к решению (12). Подставим в Тогда многочлен

[ m/ 2]

u o ^(x) = 52

s -o

формулу (12) вместо сомножителей | x | ^{2 s +2}

R m - 2 s ^(x)

(2s + 2)(2m — 2s + n)

единицу.

является гармоническим, поскольку таковы R _m- 2 s (x), и обладает свойством u o (x) = v(x) при | x | = 1. Поэтому многочлен u(x) = v(x) — u o (x) является решением задачи Дирихле (2)--(3) при Q(x) = Q _m (x). Преобразуем многочлен u o (x).

Лемма 3. Справедливо равенство

X A ^s Q m (x) u o ^(x) = X   ₄s+1

s -o

s

X

k -o

( — 1) ^k (m + n/2 — 2s + 2k — 1) | x | ^{2 k} k!(s — k + 1)!(m + n/2 — 2s + k — 1) s +₂

Доказательство. Воспользуемся леммой 2 для преобразования многочлена u o (x) из (15).

Будем иметь

u o (x) =

[ m/ 2]

X

q -o

R m -2 q ^(x) (2q + 2)(2m — 2q + n)

∞

= X q=0

2m — 4q + n — 2 (2,2) q (2q + 2)

∞

X k=0

_______________ (— 1) ^k | x | ^{2 k} A ^{q + k} Q m (x) _______________

(2,2) k (2m — 4q — 2k + n — 2,2) q + k +i (2m — 2q + n)

= ^X 1 ^X ( — 1) ^k (2m — 4q + n — 2) | x | ^{2 k} A ^{q + k} Q m (x) _n ^(2,2) q +1 ,      ^(2,2) k ^{(2m — 4q — 2k +} n ^{— 2,2)} q + k +2

q =0          k =0

Верхние пределы суммирования в последних суммах взяты равными ∞ , но фактически суммирование ограничено значениями индексов q и k, при которых deg(A ^{q + k} Q _m (x)) >  0, то есть при 2q + 2k 6 m. Преобразуем кратное суммирование в полученной выше формуле:

∞ uo(x) = XX s=0q+k=s

( — 1) ^k (2m — 4q + n — 2) | x | ^{2 k} A ^{q + k} Q m (x) (2,2) q +i (2,2) k (2m — 4q — 2k + n — 2,2) q + k +2

∞ s

X A s Q m (x) X s =0           k =0

( — 1) ^k (2m — 4s + 4k + n — 2) | x | ^{2 k} (2,2) s - k +i (2,2) k (2m — 4s + 2k + n — 2,2) s +2

∞

=X

s =0

A ^s Q m (x) 4 s +i

s

X

k =0

( — 1) ^k (m — 2s + 2k + n/2 — 1) | x | ^{2 k} k!(s — k + 1)!(m — 2s + k + n/2 — 1) s +₂

Теперь преобразуем многочлен v(x) — u o (x), который является решением задачи Дирихле (2)-(3) с Q(x) = Q m (x).

Лемма 4. Имеет место равенство

U O (X) — V(X) = ' 2 ^X (. sA^s  Z (1 — _# ) . _# ^т - ² * ^{+ п}/ 2 ^{- 1} ₍₁ —       dt

s =0                  ₀

Доказательство. Используя формулы (16) и (12), запишем:

∞

u 0 (x)

∞

— v(x) = ^X s =0

A s Q m 4 s +i

s

X

k =0

( — 1) ^k (m + n/2 — 2s + 2k — 1) | x | ^{2 k} k!(s — k + 1)!(m + n/2 — 2s + k — 1) s +₂

-

E

s =0

( — 1) ^s | x | ^{2 s +2} A ^s Q m (2,2) s +i (2m — 2s + n,2) s +i

∞

X

s =0

A s Q m 4 s +i

s +1

X

k =0

( — 1) ^k (m + n/2 — 2s + 2k — 1) | x | ^{2 k} k!(s — k + 1)!(m + n/2 — 2s + k — 1) s +₂

∞

=X

s =0

A s Q m

4 ^{s +i} (s + 1)

s +1

k =0

। | ₂ k (m + n/2 — 2s + 2k — 1)r(m + n/2 — 2s + k — 1)

^Ж            r(m + n/2 — s + k + 1)

Преобразуем внутреннюю сумму в полученном выражении. Используя связь гамма и бета функций Эйлера, можем записать следующее:

r(m + n/2 — 2s + k — 1)   B(s + 2,m + n/2 — 2s + k — 1)

r(m + n/2 — s + k + 1)             r(s + 2)

1 (7+^

i

I⁽¹ — t'

s +1 t m + n/ 2+ k - 2 s - 2

dt.

Значит, внутренняя сумма с учетом того, что kt k = t(t ^k ) 0 и бинома Ньютона имеет вид

(m + n — 2s —

¹                        s +1

1) (1 — t) ^{s +i} t ^{m + n/ 2-2 s -2} X ( — 1)^k( ^s + 1 ) k

₀                          k =0

| x | ^{2 k} t ^k dt+

⁺² Z ⁽¹

-

s +1

t) s +1 t m + n/ 2 - 2 s - 2 X

k =0

k | x | ^{2 k} t k dt =

j(1 - t) ^{s +1} (t ^{m + n/ 2 - 2 s - 1} ) 0 (i - t | x | ² ) ^{s +1} dt + 2

(1 - t) s +1 t m + n/ 2

2 s - 1

((1 — t | x | ² ) ^{s +1} ) 0 dt =

= J(1 — t) ^{s +1} d(t ^{m + n/ 2 - 2 s - 1} (1 — t | x | ² ) ^{s +1} ) — (s + 1) | x | ² J(1 — t) ^{s +1} t ^{m + n/ 2-2 s -1} (1 — t | x | ² ) ^s dt.

Поэтому, учитывая, что при n >  2, s >  0, m—2s >  0 верно равенство t ^{s +1} (1 — t) ^{m + n/ 2 2 s} 1 | 0 = 0, возьмем первый интеграл по частям. Будем иметь

(s + 1) J(1 — t) ^s t ^{m + n/ 2 - 2 s - 1} (1 — t | x | ² ) ^s ((1 — t | x | ² ) — | x | ² (1 — t))dt =

= (s + 1)(1 — | x | ² ) J(1 — t) ^s t ^{m + n/ 2 - 2 s - 1} (1 — t | x | ² ) ^s dt.

Следовательно, многочлен uo(x) — v(x) можно записать в виде uo(x) — v(x) = (1 — |x|2) X (sX^^Qm^) Z(1 — t)stm+n/2 2s 1(1 — tH^sdt = s=0                    0

= X X (XX» Ь — t) * t m - 2 ^{s + n/ 2} - ¹ (1 — »М 2М s =0                  ₀

Теперь легко непосредственно видеть, что многочлен v(x) — u o (x), удовлетворяющий уравнению Пуассона (2) с Q(x) = Q _m (x), удовлетворяет и однородному условию Дирихле (3): ^{(v(x) —} u o ^(x)) | x | =i = 0.

Итак, исходя из формулы (17) решение задачи (2)--(3) при Q(x) = Q _m (x) имеет вид

u(x) =

^{| x |} 2 ^{— 1 X} AS_O Z ^{(1 — t | x | 2 ) s (1 — t) s} ,m - 2 s + n/ 2 - 1

2    2^A Qm(x)J (2s + 2)!!(2s)!! t s=0           0

Это решение, записанное в соответствии с леммой 4 в другой форме, имеет вид

∞           s +1

u(x) = v(x) — uo(x) = X AsQm(x) X s=0          k=0

( — 1) ^{k +1} (m + n/2 — 2s + 2k — 1) | x | ^{2 k}

∞           s +1

X AsQm(x) X s=0          k=0

( — 1) ^{k +1} (2m — 4s + 4k + n — 2) | x | 2 ^k (2k)!!(2s — 2k + 2)!!(2m — 4s + 2k + n — 2,2) s +2 ^.

Пример 1. Решение задачи Дирихле (2)-(3) при Q 6 (x) = х ³ Х 2 Х ² + Х 2 Х 3 x 4 , записанное в виде (19), легко вычисляется с помощью «Mathematica»:

u(x 1 ,x ₂ ,x ₃ ,x ₄ ) = (x 4 x ₂ x ₃ + x ₂ x 2 x 4 ) ^—

¹ ₊ JX ^

32   32 /

+ (12x 2 x 2 x 3 + 6x ₂ x 2 x ₄ + 2x 2 x 4 ) x

X

₊ | x | ²      | x | ⁴ \

768   1792)

+ (24x 2 x 2 + 24x 2 x 4 ) —

1 46080

+

21504   30720

₊    ^{| x |} 6 A

129024 ) .

Из формулы (19) сразу не видно, что u(x) | x | =i = 0. Преобразуем u(x).

Теорема 3. Полином (19) можно записать в виде

u(x) = ( | x | ²

—

∞

1) X s=0

A s Q m (x) (2s + 2)!!

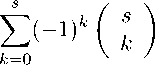
Hk

(2m — 4s + 2k + n,2) s +1

Доказательство. Преобразуем правую часть (20) к виду (19). Для этого раскроем скобки ( | x | ² — 1) и сдвинем индекс суммирования в первом слагаемом k ^ к — 1. Имеем

( | x | ²

—

∞

1) X s=0

A ^s Q m (x) (2s + 2)!!

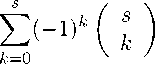
| x | ^{2 k}

(2m — 4s + 2k + n,2) s +1

= X A ^s Q m (x) X

2s + 2

s =0             k =1

( — 1) ^{k +1} | x | ^{2 k}

(2k — 2)!!(2s — 2k + 2)!!(2m — 4s + 2k + n — 2,2) _{s +}1 ⁺

—

^A s ^Q m ^(x)

2s + 2 s =0            k =0

( — 1) ^{k +1} | x | ^{2 k}

(2k)!!(2s — 2k)!!(2m — 4s + 2k + n,2) _{s +}1 ^.

Обе внутренние суммы имеют общую область суммирования 52k=p Просуммируем сначала полученные двойные суммы по этой области. Имеем

^A s ^Q m ^(x)

2s + 2 s =0    s        k =1

( — 1) ^{k +1} | x | ^{2 k}

(2k — 2)!!(2s — 2k)!!(2m — 4s + 2k + n,2)

- X s

\(2s — 2k + 2)(2m — 4s + 2k + n — 2) + 2k(2m — 4s + 2k + n + 2s)/

Приводя дроби в скобках к общему знаменателю, получим

^A s ^Q m ^(x)

2s + 2 s =0            k =1

( — 1) ^{k +1} | x | ^{2 k} (2m — 4s + 4k + n — 2)(2s + 2)

(2k)!!(2s — 2k + 2)!!(2m — 4s + 2k + n — 2,2) s +2 ^.

Вернемся к сумме (21). В первой двойной сумме мы не учли слагаемое при k = s + 1. Оно имеет вид

X a Q m x         ■   '² x ² '2

2s + 2 (2s)!!(2m — 2s + n,2) s +₁

= X A ^s Q m (x) s =0

( — 1) ^{k +1} (2m — 4s + 4k + n — 2) | x | ^{2 k}

(2k)!!(2s — 2k + 2)!!(2m — 4s + 2k + n — 2,2) s +2

I k = s +1 .

Во второй двойной сумме мы не учли слагаемое при k = 0. Оно имеет вид

∞

—X

s =0

A ^s Q m (x)             1

2s + 2 (2s + 2)!!(2m — 4s + n,2) s +1

∞

^X A ^s Q m (x) s =0

( — 1) ^{k +1} (2m — 4s + 4k + n — 2) | x | ^{2 k} (2k)!!(2s — 2k + 2)!!(2m — 4s + 2k + n — 2,2) s +2

I k =0 .

Складывая три полученных части полинома из (21), видим, что он имеет вид (19).

Получим решение задачи Дирихле (2)-(3) с неоднородным многочленом Q(x).

Теорема 4. Решение задачи Дирихле (2)-(3) можно записать в виде

u(x) =

I x I ² — 1

¹ го

Z x

₀ s =0

(1 — a | x | ² ) ^s (1 — a) ^s (2s + 2)!!(2s)!!

A ^s Q(ax)a ^{n/ 2} 1 da.

Доказательство. Пусть Q(x) — произвольный полином. Представим его в виде суммы однородных слагаемых Q(x) = ^2m Q m (x). Обозначим через u m (x) полиномиальное решение задачи Дирихле (2)-(3) с правой частью Q(x) = Q m (x). Тогда очевидно, что искомое решение имеет вид u(x) = 52m u m (x). Из формулы (18) следует, что

( \              \        |x | 2 — 1 Г (1 — a | x | ²)s(1 — a)s _m~2s          \ п/2-ь

u(x) =   um(x) = E —2— E (2s + 2)!!(2s)!! a Л Qm(x)a / da = m          m         s=0 0

J x^ ¹ XX (1 ^— a l xm^{1 —} a^{) s} _As_Q(m)a„/2-1_(iQ

2            (2s + 2)!!(2s)!! ^{Л Q(ax)a      da.}

₀ s =0

Пример 2. Пусть в задаче Дирихле (2)--(3) Q(x) = Xi, а значит, m = 1. Тогда в сумме из формулы (18) или (22) будет только один член при s = 0. Получаем

u(x) =

| ^x | ^{2 — 1}

I

αx i

a n/ ^{2 - 1} da = x   ² 1.

2           i 2(n + 2)

Если, с другой стороны, воспользоваться формулой (19), то будем иметь s = 0, m = 1 и то же решение:

-

u(x) = X i

n , n ^{+ 4} I^A _{= т} ^{| X |} 2 - ¹

2n(n + 2) ⁺ 2(n + 2)(n + 4) | x |       x i 2(n + 2)^.

Рассмотрим теперь следующую задачу Дирихле для уравнения Лапласа в единичном шаре Q:

Лv(x) = 0,x Е fi; v|dQ = P(x)|dQ, с полиномиальным граничным значением P(x) и при n > 2.

Сформулируем утверждение, дополняющее утверждение теоремы 4.

Теорема 5. Решение задачи (23) можно записать в виде уРЛ — р/х\ _ |x| — 1 Z X (1 — a|x| ) (1 — a) As+1P(an/et-^-ida(24)

v(X) = P(X)       2 J / v (2s + 2)!!(2s)!! Л P(aX)a     da.(24)

₀ s =0

Доказательство. С помощью формулы (22) найдем решение следующей задачи Дирихле:

Лu(x) = ЛР (x),x Е fi, u |_x| =i = 0.

Имеем

Ц_ХА ₌ 1 x2 —1 Z X X ^{(1 — a | x | 2 ) s (1 — a) s} As+i_P(_an/_a-i^a_a ^u(x)       2             (2s + 2)!!(2s)!!   ^Л P ^{( )a}

₀ s =0

Тогда следующий полином:

₍ \       \      \       \   ^{| x |} 2 ^{— 1} Z X X ^{(1 — a | x | 2 ) s (1 — a)} s As+ip(_an/a-l^da

^v(x) = P ^{(x) —} u^(x) = P ^(x)      2 J у (2s + 2)!!(2 _s )!!   ^Л   P^{(ax)a      da}

₀ s =0

является гармоническим, поскольку Лv(x) = ЛР(x) — Ли(х) = 0 и удовлетворяет граничному условию v(x) | x | =i = P (x) |_x| =i - Решение задачи (23) найдено, и оно имеет вид (24).

Пример 3. Пусть в задаче (23) P (x) = x 2 . Тогда в сумме из формулы (24) будет только один член s = 0. Поэтому

v(x) = x ² — |xL— 1 j I • 2a ^{n/ 2-1} da = x ² + 2(1 — | x | ² ).

Объединяя теоремы 4 и 5 получим следующее утверждение.

Теорема 6. Решение задачи Дирихле:

^Au(x) = Q(x)^,x G ^Q, ^u | d Q = P(x) | d Q ,                            (25)

в единичном шаре Q можно записать в виде

u(x) = P (x) +        Z X (^ - SO^^Is - j a- A s (Q - AP)(ax)a "^{/ 2 - 1} da       (26)

0 s =⁰

Доказательство. Решение задачи (25) можно разложить на сумму решений двух задач (23) и (2)--(3). Сумма этих решений (24) и (22) и дает искомую функцию (26).

• III.    Полиномиальные решения третьей краевой задачи для уравнения Пуассона

Рассмотрим следующую обобщенную краевую задачу для уравнения Пуассона:

∂

Au = f (x), x G Q; P m ( dV / U | d ^ = ^(s), s G d Q,                     (27)

в единичном шаре Q. Здесь d/dv — производная по направлению внешней нормали к единичной сфере Q, P m (t) — многочлен m-й степени с действительными коэффициентами и t G R. Предположим, что ^ G C (dQ), а f (x) — многочлен произвольной степени.

Пусть V[f](x) — объемный потенциал с плотностью f (x), то есть

• V[f](x) = — — [ E(x£f (Ж                       (28)

ωn dQ где E(x,e), как и в (1), элементарное решение уравнения Лапласа.

Рассмотрим некоторый полином Q(t) степени m и A G R. Запишем Q(t) в виде Q(t) = Pmo ai(t — A)i, где ai G R. Поставим ему в соответствие другой полином Q(x)(t) степени m — 1 по формуле m-1

Q ^{( A ) (t)} = X a i +i ^{(t - A)} i + a i ^- 2a ₊ П _— 2.

i =1

Ясно, что если A — корень полинома Q(t), то a o = 0 и Q ^{( x )} (t) = Q(t)/(t — A).

Определение 1. Пусть P _m (t) = P m Lo P k t ^k — полином из задачи (27). Назовем факториальным полиномом P [ _m ] (t), соответствующим полиному P _m (t), следующий полином: P [ _m ] (t) = P m =o P k t ^{[ k ]} , где t ^{[ k ]} = t(t — 1)...(t — k + 1) — факториальный одночлен.

Обозначим так же P m (t) = P m (t)/(t — A), где A — некоторый корень полинома P m (t). Введем в рассмотрение множество I неотрицательных целых корней факториального полинома P [ _m ] (t), то есть множество I = {k G N o : P [_m] (k) = 0 } . Справедливо утверждение [7].

Теорема 7. Решение задачи (27) существует тогда и только тогда, когда выполнено условие

A G I ^ V H x (x), j H _A (x)^(x)dx = j H x^ P m (Л + 2)f(x)dx,

d Q

Q

где H x (x) — произвольный однородный гармонический полином степени A.

Пример 4. Рассмотрим следующую задачу:

d ² u

Au = f(x), x G Q;           = ^(s), ⁸ G d Q.

OV ² | d Q

Для нее имеем m = 2, P m (t) = t ² , P [ m ] (t) = t ^[2] = t(t - 1), I = { 0,1 } , P m (t) = t - 1, P m ] (t) = t.

Условия разрешимости задачи (30) имеют вид j ^(x^dx=j Pm(л+2)f (x)dx=j

(Л + 1)f (x)dx,

d Q          Q

Q

V i,

j x i ^(x)dx = j

X i Pн(Л + 2)f (x)dx

d Q

Q

j x _i (Л + 2)f (x)dx.

Q

Теперь рассмотрим третью краевую задачу в единичном шаре Q:

Au(x) = Q(x),x G Q;

∂u

Ц^^- + Au ∂ν

| d Q

= ^P(x) | d Q

с полиномиальными правой частью Q(x) и граничными данными P (x) и при ц, A G R. Здесь v — внешняя единичная нормаль к dQ. Эта задача является частным случаем задачи (27) при m = 1 (если ц = 0) и P _m (t) = цt + A. В этом случае P [ _m ] (t) = P _m (t), а поэтому единственный корень многочлена P [ _m ] (t) имеет вид A q = -A/ц и Pm^t) = Ц. Поэтому при ц = 0 условия разрешимости задачи (31) имеют следующий вид: если A q = -A/ц G N q , то для любого Н _Л 0 (x) — однородного гармонического полинома степени A q — должно быть выполнено равенство (см. условие (29))

j H o P(x^)dx = ^Н(^x)Q(^x)dx.

d Q

Q

Решение задачи (31) единственно с точностью до полинома вида u(x) = V[Q](x) + Нл ₀ (x), если A q G N q . Если A q G N q , то решение существует и единственно при любых полиномах P (x) и Q(x). Как же находить это решение?

Теорема 8. Пусть полиномы Q(x) и P (x) разложены по своим однородным составляющим:

dd

Q(x) = X Q m (x),   P (x) = X P m (x).

m =Q               m =Q

Решение третьей краевой задачи (31) существует, если при условии Aq = -A/ц G Nq для любого однородного гармонического полинома Нл0 (x) выполнено равенство j Нл0 (x)P (x)dx=ц|НЛ0 (x)Q(x)dx.

d Q

Q

Это решение единственно с точностью до полиномов вида u(x) = V[Q](x) + Нл ₀ (x), где H k (x) — произвольный однородный гармонический полином степени к. Если A q / N q , то решение существует и единственно при любых полиномах Q(x) и P (x). Решение третьей краевой задачи (31) можно записать в виде

d

u(x) = X m=-2

P m +2 (x)

(m + 2)ц + A

^ s +1

+ XX ( - 1) ^{k +1} x s =Q k =Q

(2m - 4s + 4k + n - 2) | x | ^{2 k} A ^s ((A + (m + 2)ц)Q m (x) - AP m +2 (x)) A ^X (A + (m - 2s + 2k)ц)(2k)!!(2s - 2k + 2)!!(2m - 4s + 2k + n - 2,2) s +2) ^.

Прежде чем приступить к доказательству теоремы, приведем пример вычисления решения конкретной задачи:

∂u

Au(x) = x 3 ,x G Q C R⁴;   I —+ 2u I    = x { x 2 | d Q

Vdv     Z|dQ по формуле (32) с помощью пакета «Mathematica». Решение имеет вид

u(x) = ^1^(2880x 1 x 2 + (2x 2 + x 2 - 4x 2 )(216 - 240 | x | ² + 72 | x | ⁴ )+

+(x 1 + 6x 1 x 2 - 4x 3 )(320 - 240 | x | ² ) - 60 + 54 | x | ² - 20 | x | ⁴ + 3 | x | ⁶ ).

Доказательство. Условия существования решения задачи (31) следуют из теоремы 7 и обсуждались перед формулировкой этой теоремы. Пусть u(x ) — решение задачи (31). В силу теоремы 1 функция u(x) может быть представлена как сумма полинома (6) и некоторой гармонической функции u o (x). Поскольку u o (x) представляется в единичном шаре Q в виде равномерно и абсолютно сходящегося ряда, то функция u(x) в Q также есть сумма равномерно и абсолютно сходящегося ряда u(x) = ^Z^oи к (x), где и к (x ) — однородные полиномы степени k.

Далее, поскольку на д Q имеет место равенство du/dv = Ли, где Ли = ^2П₌₁ x^ X i , то задача (31) эквивалентна следующей задаче:

Au(x) = Q(x),x G Q; (^Ли + Лu) | д Q = P (x) | d Q .

Нетрудно видеть, что справедливы равенства

∂2        ∂2  n                    n dx2 Ли = dx2 / x XiUxi = 2Uxj xj + / у Xi(uxi )xj xj = 2Uxj xj + ЛиХ xj j           j i=1                      i=1

и, значит:

АЛи = 2Аи + ЛАи = (Л + 2)Аи.

Применим оператор ^Л + А + 2^ к уравнению из (33). Если обозначить Q i (x) = (^Л + Л + 2^)Q(x), то будем иметь

(^Л + Л + 2^)Аи = ^(Л + 2)Аи + ЛАи = А(^Ли + Ли) = Q 1 (x)

для x G Q. Обозначим v = ^Ли + Ли. Тогда функция v(x) является решением следующей задачи Дирихле:

Av(x) = Q i (x),x G Q; V | d Q = P (x) | a n -

Поэтому в соответствии с теоремой 6 запишем:

v(x) = P (x) + I x^ - ¹ Zz XX ⁽¹ - ^{a |} x ^l2 ? s/ ,1 - a ^{) S} A ’ (Q 1 - AP )Vax)a n^{/ 2-1} da.        (34)

2 J „_n    (2s + 2)--(2s)--

₀ s =0

Для нахождения функции u(x) необходимо решить уравнение v(x) = (^Л + Л)u(x). Если разложить полином v(x) по однородным составляющим и вспомнить что функция u(x) тоже есть сумма однородных полиномов d+2

v(x) = ^Vk (x), u(x) = ^ик (x), k=0

то тогда будем иметь d+2

• У1 V k (x) = ^(k^ + Л)и к (x).

k=0

Здесь, поскольку deg Q i 6 deg Q и deg v 6 max { deg P, deg Q i + 2 } , то имеем deg v 6 max { deg P, deg Q + 2 } 6 d + 2. По теореме о единственности разложения функции в ряд Тейлора, при k^ + Л = 0 будем иметь

^V k ^(x)

^{и к (x)} = k^ + Л^.

Если окажется, что —А/ц G Ng, то есть при некотором целом неотрицательном к будет kц + Л = 0, то в этом случае должно быть выполнено равенство Vk(x) = 0, иначе v(x) не удовлетворяет уравнению v(x) = (цЛ + А)u(x) ни при какой u(x). Итак, d+2

u(x) = X k=0

V k (x) kц + А

Преобразуем это решение. Рассмотрим простейший случай, когда Q(x) = Q m (x) и P (x) = P m +2 (x) — однородные полиномы. Решение задачи (31) в этом случае обозначим u ^{( m )} (x). Промежуточный полином Q i (x) будет иметь вид

Q 1 (x) = (цЛ + А + 2ц)Q m (x) = (А + (т + 2)ц)Q m (x).

Тогда, в соответствии с формулой (19) и доказательством теоремы 5 решение v ^{( m )} (x) из формулы (34) запишется в виде

V ^{( m )} (x) = P m +2 (x) + X Д ^в ((Л +(m + 2)ц)Q m (x) — AP m ₊2 (x)) X s =0

X

s +i X k =0

( — 1) ^{k +1} (2m — 4s + 4k + n — 2) | x | ^{2 k} (2k)!!(2s — 2k + 2)!!(2m — 4s + 2k + n — 2,2) s +2 ^.

Значит, решение (35) перепишется в форме

u ^{( m )} (x)

P m +2 (x)

(m + 2)ц + А

∞

+ X A s ((А + (m + 2)ц)Q m (x) — AP m +2 (x)) x s =0

s +i