Построение распознавателя языка Yard по синтаксической граф-схеме

В настоящее время языковые технологии активно включаются в различные сферы нашей жизни, например, в комплексные системы производственной сферы [1], при сопоставлении образцов в анализе ДНК, в задачи компьютерной безопасности [2] и во многие другие, что привело к развитию современных транслирующих систем, использующих принцип синтаксического управления для производства программ обработки данных и ориентированных на разнообразный набор вычислительных устройств.

Обработка данных по такой технологии управляется синтаксической структурой этих данных, которые традиционно описываются формальными грамматиками и чаще всего контекстно-свободными грамматиками и их обобщениями.

Множество современных искусственных языков, языки программирования (Си, С++, языки семейства Microsoft.Net (C#, F#, Visual C++, Visual C#, Visual F#), Python2, Python3, Java, Haskel, Rust, Kotlin, Go, Perl, PHP, R, JavaScript, Swift, Objective-C, Pascal, Basic, D и другие), языки разметки графов (DOT, Trivial Graph Format, GraphML и другие) порождаются контекстно-свободными грамматиками в регулярной форме (КСР-грамматиками). Возникает проблема синтаксического анализа, разбора подобных языков и построения распознавателей для эффективного опре- деления принадлежности цепочек (предложений) языку.

В статье рассматривается задача построения распознавателя для произвольной КСР-грамматики на примере формальной грамматики языка программирования Yard с определенными функциями, реализация которого предполагает в дальнейшем создание оптимального генератора кода для специальных нестандартных чипов.

1. Современное состояние дел

Для решения задачи построения трансляции используются различные технологии разработки трансляторов, наиболее распространенными из которых являются средства, основанные на применении различных подклассов контекстно-свободных (КС) грамматик для описания входного языка [3–6]:

• •    YACC (Yet Another Compiler-Compiler) — 1975 — это a parser generator: находит иерархическую структуру программы.

• •    Lex — 1978 — это a lexical analyzer generator: разбивает исходный файл на лексемы или другие лексические единицы.

• •    Lex &YACC — 366 страниц, 2-е издание. (1992).

• •    Flex (Fast Lexical Analyzer), (1987) — генератор сканера, release 2.6.4, May 6, 2017 — TeX manual (287K).

• •    GNU Bison (1985), YACC (Yet Another Compiler Compilers) — совместимый генератор анализатора — ASCII (548K).

• •    ANTLR (ANother Tool for Language Recognition). — Руководство по ANTLR 4–328 страниц. 2 ^nd ed. 2013.

Очевидно, что для построения современных трансляторов использование стандартных инструментов является утомительным и трудоемким делом.

В качестве перспективной формальной базы для построения трансляторов в СПИИРАН разработана методика, основанная на использовании грамматик с обобщенными регулярными выражениями и атрибутами в виде семантик для представления контекстных ограничений и синтаксических граф-схем. Эта методика поддержана пакетом программных приложений, реализованных на платформе Microsoft.NET. В качестве основы взят код инструментального средства SynGT (SynGT Graph Transformation), разрабатываемого в СПИИРАН с 2000 г. [8].

• •    Формальной моделью методики построения языковых процессоров, описанной в [7] и реализованной в SynGT, являются регулярные выражения как средство описания языка и конечный автомат в качестве адекватного средства его обработки.

• •    Теоретическим обоснованием этой модели являются теорема С. Клини и ее следствия о том, что класс регулярных множеств является минимальным классом, содержащим все конечные множества, замкнутым относительно операций объединения, конкатенации и замыкания [9].

• •    Регулярные множества распознаются конечными автоматами и представляются регулярными выражениями.

Использование этой модели ограничено ее применением лишь к регулярным языкам, поэтому модель обобщена до класса КСР-языков с использованием специальных магазинных автоматов [10; 8].

КСР-язык порождается КСР-грамматикой — обобщением КС-грамматики.

Основные определения были даны в работах [8; 11]. Напомним их неформально.

Как известно [9], формальным языком является набор цепочек языковых токенов (лексем или терминалов) в соответствии с грамматикой языка. Грамматика языка состоит из контекстно-свободной части в виде КС-правил и контекстно-зависимой части (ограничений).

КС-правила представлены в форме с обобщенными регулярными выражениями (КСР-правила):

Нетерминал : обобщенное регулярное выражение .

Регулярные выражения состоят из токенов (лексем), нетерминалов, регулярных операций (конкатенация, альтернативный выбор и обобщенная итерация), пустой цепочки ("") и скобок ("(" и ")"):

• -    Конкатенация (“,”): A,B = AB.

• -    Альтернативный выбор (“;”): A;B = либо A, либо B.

• -    Обобщенная итерация ( “#“): A#B = A; ABA; ABABA; ABABABA;

• -    Унарная итерация Клини (“*“): А* =_; A; AA; AAA;_

• -    Возможно пустое множество цепочек X: [ X ] = (X;).

2.    Обобщение регулярной модели

Обобщение конечно автоматной модели обработки языков сводится к следующему:

• •    вводится итерация с разделителем (#) или обобщенная итерация, или итерация Г. С. Цейтина, которая не расширяет множество регулярных слов и может быть определена через традиционную (одноместную) операцию Клина (*) как (P#Q)=P,(Q,P)*. Она удобна при работе со стеком и частично решает задачу минимизации регулярного выражения по числу вхождений символов из объединенного алфавита всех символов грамматики;

• •    КСР-грамматика — обобщение КС-грамматики. Класс языков не расширяет, но снимает лишнюю структурированность языка;

• •    синтаксическая граф-схема (СГС) — графический аналог КСР-грамматики, стартовый объект для синтеза распознавателя (анализатора) языка, в терминах вершин которой удобно формулировать свойство детерминированности языка и возможные типы конфликтов (Shift/Reduce). СГС является промежуточной моделью между порождающей структурой, грамматикой и распознающей машиной, МП-автоматом.

3.    Синтаксическая граф-схема (СГС)

Cинтаксические граф-схемы (СГС) — это аналог диаграмм Вирта. Каждому нетерминалу соответствует одна компонента такой диаграммы или одно правило КСР-грамматики, правая часть которого является обобщенным регулярным выражением относительно символов объединенного алфавита грамматики. В объединенный алфавит грамматики входят алфавиты терминалов, нетерминалов, семантик и возможно предикатов.

СГС создается рекурсивно из графов для элементарных регулярных выражений и бинарных операций (рис. 1).

k Semantic

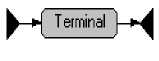
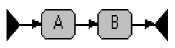
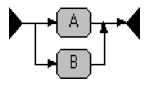
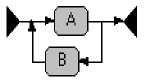
Рис.1. Графы для элементарных регулярных выражений

При разработке транслятора необходимо решать следующие задачи:

• •    упрощение грамматики;

• •    регуляризация грамматики;

• •    разрешение конфликтных ситуаций, возникающих в процессе построения распознавателя и анализатора и связанных с языковой неоднозначностью (как синтаксической, так и семантической) и недетерминированностью магазинного автомата.

Фундаментальные работы таких авторов, как:

• •    Н. Хомский — иерархия грамматик;

• •    С. К. Клини — регулярные множества и регулярные выражения;

• •    Г. С. Цейтин, А. П. Ершов, С. С. Лавров, Б. К. Мартыненко [10] — технология программирования;

• •    Д. Кнут, А. В. Ахо, Д. Ульман — теория языков и автоматов;

• •    Грегори Розенберг и Арто Саломаа — Handbook of Formal Languages составляют основу современной теории построения трансляторов языка, которую необходимо расширять в соответствии с требованиями практики во всех областях применения наличием инструментария и методов для автоматизации реализуемого языка в условиях жестких временных ограничений.

4.    Инструментальная система SynGT

Основные модули:

•

-

текстовый редактор:

проверяет корректность регулярных выражений (конечно- автоматная модель);

• -    формирует приведенную (well-formed) грамматику (удаление недостижимых нетерминалов, нетерминалов с пустым порождением, цепные правила и т.д.);

• -    осуществляет редактирование словарей символов и др.);

• •    графический редактор:

• - осуществляет пользовательский интерфейс для обработки грамматики;

• • эквивалентные синтаксические преобразования:

• - формируют грамматику для построения детерминированного процессора;

• • генератор тестов:

  – генерирует набор прототестов для получения их замыкания [12].

5.    SynGT: базовые функции и решаемые задачи

Алгоритмы, реализованные и постоянно пополняемые в SynGT, выполняют следующие эквивалентные преобразования над регулярными выражениями и КСР-правилами:

• -    подстановка вместо нетерминала его порождения;

• -    исключения лево- и праворекурсивных нетерминалов из грамматики с обобщенной итерацией;

• -    объединение общих префиксов в графе для нетерминала;

• -    удаление повторяющихся альтернатив для нетерминала;

• -    удаление крайних рекурсий для самовложенных нетерминалов;

• -    свертка регулярного подвыражения в новый нетерминал и создание правила в грамматике для нового нетерминала с регулярным подвыражением в его правой части;

• -    удаление лишних правил.

В результате должны быть решены следующие задачи:

• 1.    После обработки текста КСР-грамматики получаем правильную запись регулярных выражений. Все входящие нетерминалы являются продуктивными, т. е. порождают непустые цепочки, и достижимыми, то есть участвуют в выводе цепочек языка.

• 2.    Преобразование текстового представления регулярного выражения в графическое (задача размещения граф-схемы на экране).

• 3.    Реализация стандартных редакторских функций и функции подстановки вместо нетерминала его регулярного выражения, а также сведения подвыражения в новый нетерминал и добавление его в список нетерминалов грамматики.

• 4.    Обратное преобразование граф-схемы в текстовое регулярное выражение.

• 5.    Эквивалентные преобразования КСР-грамматики и синтаксической граф-схемы (удаление рекурсий).

• 6.    Регуляризация КСР-грамматики.

• 7.    Синтез (построение) конечной таблицы всех состояний МП-автомата, распознающего формальный язык.

• 8.    Тестирование. Построение списка прототестов и их замыкание для получения множества «хороших» и «плохих» тестов [12].

6.    Yard — пример формального языка

Набор функций, реализованных в SynGT, служит основной цели — автоматизированное преобразование КС-грамматики для ее упрощения и максимальной регуляризации, то есть превращение синтаксической граф-схемы грамматики в минимальный набор конечных автоматов для построения анализатора языка. Если КС-грамматика порождает регулярный язык, то синтаксическая граф-схема вырождается в один граф, представляющий эквивалентное регулярное выражение. Алгоритм и примеры даны в работе [8].

Рассмотрим технику построения распознавателя формального языка Yard с использованием пакета модулей SynGT.

Язык Yard содержит:

54 лексемы:

• •    generics: '' '' '' '' '' '';

• •    зарезервированные слова : 'all' 'array' 'begin' 'bitrow' 'bool' 'byte' 'char' 'const' 'do' 'double' 'dword' 'else' 'end' 'endif' 'for' 'if' 'in' 'inout' 'input' 'int' 'longint' 'node' 'of' 'out' 'output' 'pointer' 'program' 'real' 'shortint' 'static' 'string' 'then' 'to' 'word';

• •    индиканты: '(' ')' '*' ',' '.' '..' ':' ':=' ';' '@' '[' ']' '^' '=';

19 нетерминалов : ArraySpecification CompoundStatement Constant ConstantDeclaration Declaration FormalBounds FormalComponent ForStatement LinkList NetExpression NodeDeclaration Operand PointerSpecification PrimitiveResource Program SliceConstructor Specification SubscriptExpression VariableDeclaration.

Начальный нетерминал: Program.

• 38 (semanitcs), разбросанных по грамматическим правилам. Каждой семантике предшествует знак «$»

7.    Контекстно-свободные правила в регулярной форме

• 1.    ArraySpecification : 'array' FormalBounds FormalComponent ; '' [ FormalBounds ] [ FormalComponent ] .

• 2.    Constant : '' ; '' ; '' ; '' .

• 3.    CompoundStatement : 'begin' ( NetExpression )*( ';' ) 'end' ; 'if' NetExpres-sion 'then' ( NetExpression )*( ';' ) [ 'else' ( NetExpression )*( ';' ) ] 'endif' .

• 4.    ConstantDeclaration : 'const' ( '' '=' Operand )*( ';' ) .

• 5.    Declaration : ConstantDeclaration ; VariableDeclaration ; NodeDeclaration

• 6.    FormalBounds : '[' [ ( '' ; Constant [ '..' Constant ] )*( ',' ) ] ']' .

• 7.    FormalComponent : 'of' Specification .

• 8.    ForStatement : 'for' 'all' '' 'do' ( NetExpression ; CompoundStatement

• 9.    LinkList : ( ( 'in' ; 'out' ; 'inout' ) ( ( '' )*( ',' ) ':' Specification )*( ';' ) )*( ';' ) .

• 10.    NetExpression : ( *( '' ) Operand [ PrimitiveResource ] )*( '' ; '=' ) ; Operand [ PrimitiveResource ] ':=' NetExpression ; ForStatement .

• 11.    NodeDeclaration : 'node' VariableDeclaration ; [ 'static' ] 'node' '' [ '(' ( '' )*( ',' ) ')' ] ; CompoundStatement .

• 12.    Operand : '' *( SliceConstructor ; '^' ) ; '(' NetExpression ')' ; '' [ '(' ( '' )*( ',' ) ')' ] ; Constant .

• 13.    PointerSpecification : 'pointer' [ [ 'to' ] '' ] .

• 14.    PrimitiveResource : '@' ( 'input' ; 'output' ; '' ) .

• 15.    Program : [ 'static' ] 'program' '' '(' ( 'input' ; 'output' ; '' )*( ',' ) ')' *( ';' Declaration ) ';' CompoundStatement '.' .

• 16.    SliceConstructor : '[' ( SubscriptExpression )*( ',' ) ']' .

• 17.    Specification : ( 'bool' ; 'byte' ; 'char' ; 'dword' ; 'int' ; 'longint' ; 'shortint' ; 'word' ; 'bitrow' ; 'double' ; 'pointer' ; 'real' ; 'string' ) [ '*' '' ] ; PointerSpecification ; ArraySpecification .

• 18.    SubscriptExpression : '' ; 'all' ; NetExpression ; '(' ( SubscriptExpression )*( ',' ) ')' .

• 19.    VariableDeclaration : ( ( '' )*( ',' ) ':' Specification )*( ';' ) .

8.    Контекстные условия (семантики)

) .

38 semantics: $array1 $array2 $bound1 $bound2 $constant $constdecl $do $dyadic $else $endif $forall $if $link $monadic $netexpr $node $operand $operand1 $operand2 $pointer1 $pointer2 $primitive1 $primitive2 $program1 $program2 $program3 $slice1 $slice2 $slice3 $spec1 $spec2 $static $subscript1 $subscript2 $then $up $vardecl1 $vardecl2 расставлены внутри правил, например, семантика $vardecl1 проверяет, что каждая переменная описана в программе.

Семантики могут вставляться в текст правила для нетерминала либо непосредственно на дугах в граф-схеме.

Например, проверка на единственность описания каждого тэга.

VariableDeclaration : ( ($vardecl1 '' )*( ',' ) ':' Specification $vardecl2)*(

';' ) .

Operand : $operand1 ( '' *( SliceConstructor ; '^' ) ; '(' NetExpression ')' ;

'' [ '(' ( '' )*( ',' ) ')' ] ; Constant ) $operand2 .

9.    Проверка грамматики Yard в SynGT

Первоначально c помощью SynGT проверяется корректность записи регулярных выражений, удаляются лишние правила (например, нетерминал LinkList оказался недостижимым) (рис. 2–4).

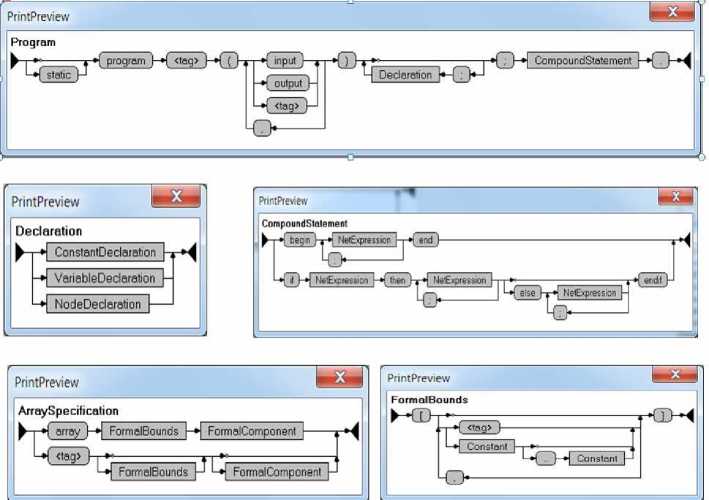
Рис. 2. SynGT-1. Графы для нетерминалов грамматики Yard

PrintPreview

NetExpression

- y*- *°---- I H Operand h -* »                   *

Ц<орега^оп>] *-1                 PrimitiveResaurce P

Ц } *-----------------------------------------

-* | Operand | -p *>                 * 4~^ W NelExpressi

PrimitiveResource P

- H ForStatement | -----------------------------------------

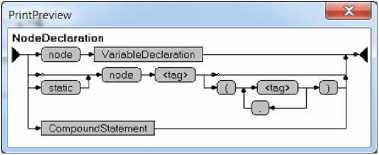
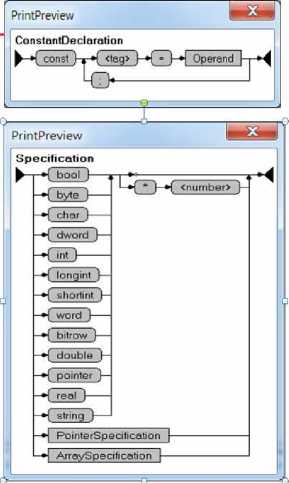
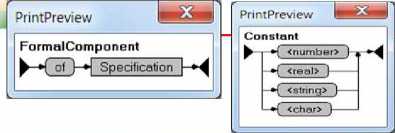
Рис. 3. SynGT-2. Графы для нетерминалов грамматики Yard

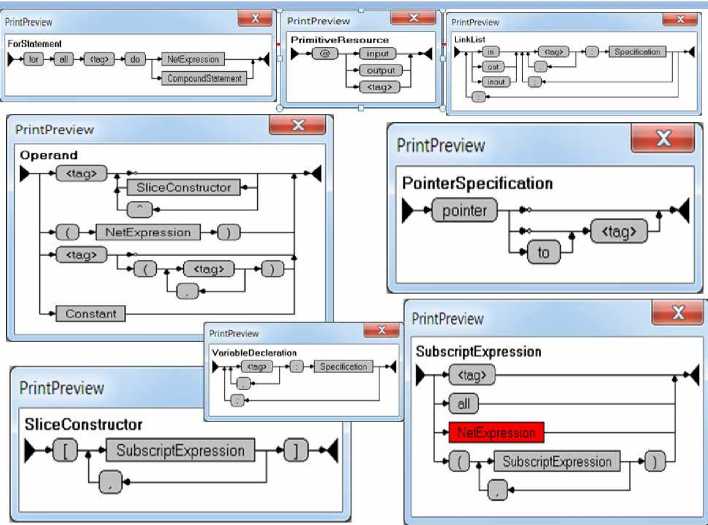
Рис. 4. SynGT-3. Графы для нетерминалов грамматики Yard

Далее проводится анализ на рекурсивности (рис. 5), удаляются леворекурсивные нетерминалы грамматики, грамматика тестируется на ее принадлежность к классу LL ( k ). Если k > 1, то выполняется эквивалентное преобразование для приведения грамматики в класс LL (1). Затем если необходимо, то выполняется ее регуляризация (сведение к минимальному числу правил) (рис. 5).

Nonterminal                        | Value                                                                  |l_eft recurs,Recursion, Right Reef

[Program_______________________________________| (";' stati c‘),1 p rog ram',' ',1 (', (' in p ut‘;1 о utput';' ')#',',')', "#('; IDecl arati о n),

Declaration	ConstantD eclaration:VariableDecl arati on;Node Declaration.
Co rn p о u n d State m e nt	'begin',NetExpression#':','end';'if,NetExpression,'then',NetExpression#':',("		indirect	indirect
ArrayS p e cifi cati о n	'array',FormalBounds.FormalComponent‘'.(";FormalBounds),(";Form		indirect	indirect
Form al В ounds	'[', (";(' ';Constant(l';1. ,',Co nstant))#V), T-
Form al Component	'of'.Specification.		indirect	indirect
NetExpression	("#''.Operand,(";PrimitiveResource))#,';Operand,(";	indirect	direct	direct
Constant	‘ < n u rn b e r >';1< re al >';' < st ri n g >';' < ch ar >'.
ConstantD eel arati о n	■con st',(' 7=I Operand)#';'.
Operand	''."#(5 lice Constructor;^ ');■('. NetExpres sion?) ';'',(";'(',''#',7)');	indirect	indirect	indirect
Vari able Declaration	(''#',',''.Specification)#';'.
NodeDeclaration	■node'. Variable Declaration; ("/static'),' no de7',(";'(7'#7,')l);Comp
Specification	('bool':'byte':'char';'dword';'int':'longint';'shortint';'word';'bitrow';'double';'poin		indirect	indirect
ForStatement	'for','air,'','do'.(NetExpression;CompoundStatement).		indirect	indirect
LinkList	(('in';' out';'inout'),(''#'.',':', Specification)#';')#';'.
Pri mitive Resou rce	'©'.('inputl'outputlktagx').
SliceConstructor	'['.SubscriptExpression#'.',']'.		indirect
F'ointerSpecification	' p о i nte r', ("; ("; 'to'),' ').
SubscriptExpression	'';'aH';NetExpression;'(lSubscriptExpression#',',')'.	direct	direct
EO Gram

Рис. 5. Анализ на рекурсивность в SynGT

10.    Реализация алгоритма построения распознавателя языка Yard

Формальные определения состояний в граф-схеме и основные алгоритмы построения распознавателя формального языка даны в [11]. В данном разделе кратко опишем реализацию алгоритмов построения распознавателя, выполненную студентами 3-го курса СПбГУ Кравченко Евгением и Ерзиковой Юлией .

Алгоритм построения распознавателя языка Yard состоит из трех основных этапов:

Этап 1. Приведенную грамматику Yard, полученную из SynGT, преобразовать в граф-схему в линейном представлении согласно заданным шаблонам [11].

Э тап 2. Построить стек состояний, удалив эквивалентные состояния.

Этап 3. Построить программу-распознаватель и провести несколько экспериментов.

Для построения синтаксической граф-схемы были использованы следующие программные элементы, которые опишем далее.

С помощью перечисления зададим всевозможные типы элементов, содержащихся в строке: символьная строка, операция, адрес перехода и выход из правила.

Класс TableElement описывает элемент линейного представления граф-схемы. Для данного элемента будем хранить его тип и само значение элемента. При этом если это адрес перехода, то для него поле lexeme является пустым, а поле numb заполняется числовым значением. Для остальных типов элементов поле numb = -1, а lexeme инициализируется соответствующей строкой.

enum element_type {String, Operator, Address_link, Ex};

class TableElement

{ element_type kind;

string lexeme;

int numb;

public:

TableElement (element_type x, string y=””, int z=-1): kind(x), lexeme(y), numb(z) {} }

Класс LinearGraphScheme, являющийся дружественным с классом TableElement, ответственен за построение итоговой граф-схемы в линейной форме по КСР-грамматике. Основным методом является FormResultTable, который организует обработку правил входной КСР-грамматики по принципу, описанному в разделе «Описание структуры программы и представление данных в ней».

Шаг 1. В ходе анализа каждого КСР-правила для него вход по нетерминалу и разветвление путей заносится в очередь. При достижении конца правила достаем из очереди первый элемент и для него выполняем рекурсивный вызов метода FormResultTable. Следующие два метода используются для определения принадлежности текущей лексемы к определенному типу(element_type) и развертки операции по заданным шаблонам.

class LinearGraphScheme

{private:

vector Input_CFR_Rules;

vector ResultTable;

public:

vector< TableElement> FormResultTable(string current_st, int len);

element_type GetElementType(string s);

string template_operator(string A, string B, Operator C)

TableElement GetValue(int TableIndex);

element_type GetType(int TableIndex);

TableElement Start_of_Rule(string nonterm);

TableElement End_of_Rule(string nonterm); friend class TableElement;

}

По заданным индексам может быть найдено значение и тип элемента в массиве, также по нетерминалу можно восстановить элементы начала и конца, задаваемого правила.

Для построения стека состояний были использованы следующие программные элементы:

Класс FormStackOfState отвечает за построение стека состоянии распознавателя КСР-цепочек. Основным методом является FormStateStack , который с помощью построенной ранее линейной граф-схемы заполняет stack States по алгоритму, подробно описанному в разделе «Описание структуры программы и представление данных в ней».

Шаг 2. Попутно в вектор State_Address помещаются адреса всех состояний из стека. Дополнительно введенные методы Get_State и Get Address предназначены для сопоставления состояния граф-схемы и адреса элемента в стеке.

Данный класс является фундаментом для осуществления последующей проверки на принадлежность цепочек символов КСР-грамматике.

Для построения последовательности состояний анализатора были использованы следующие программные элементы:

Класс CheckCharacterStrings отвечает за распознавание входных цепочек символов.

Конструктор этого класса инициализирует и получает построенный на предыдущем шаге стек состояний. Многомерный контейнер Trajectory отвечает за хранение путей в процессе передвижения по состояниям, т. к. таких путей может быть не один, а несколько.

class FormStackOfState

{ private:

stack States;

vector State_Address;

LinearGraphScheme grapth_scheme;

public:

stack FormStateStack(LinearGraphScheme

GrapthScheme);

int Get_State (int Address);

int Get_ Address(int State);

}

Также класс CheckCharacterStrings обладает методом Check , который принимает на вход цепочку символов и осуществляет ее проверку на принадлежность данной КСР-грамматике.

Для того чтобы можно было отследить до какого момента (состояния) рассматриваемая цепочка выводима в заданной КСР-грамматике, был добавлен метод NextState , при каждом вызове которого объект класса переходит на одно состояние вперед. В свою очередь, за вывод построенного для цепочки пути отвечает метод WritePath .

Эффективность данного способа организации распознавания цепочек достигается за счет того, что построенный стек состояний инициализируется один раз при создании объекта класса и хранится в течение всего периода работы программы. Поэтому проверка входной цепочки вынесена в отдельный метод класса.

Class CheckCharacterStrings

{ private:

FormStackOfState Stack_of_state;

vector> Trajectory;

int NumberOfPaths;

int CurrentState;

public:

CheckCharacterStrings(FormStackOfState StackOfState);

bool Check(string CharacterString);

int NextState();

void WritePath();

}

Реализация граф-схемы в линейной записи основана на рекурсивном сведении более сложных случаев к базисным элементам, которые представлены следующими шаблонами:

Таблица 1

Шаблоны для представления операций в граф-схеме

1) a , b .	Адрес в массиве	1	2	3
	значение	a	b	.
2) a ; b .	Адрес в массиве	1	2	3	4	5	6	7
	значение	<	6	a	↓	7	b	.

3) a#b .	Адрес в массиве	1	2	3	4	5	6	7
	значение	a	<	7	b	↓	1	.

В результате граф-схема грамматики Yard представлена на рис. 6 в компактном двумерном виде, где самый левый столбец вместе с верхней строкой формирует адрес в массиве — машинном представлении граф-схемы.

	0	1	2	3	4	5	6	7	8	9
0	<	3	static	program		(		16		13
1	input	4	14	output	4	17		•<	22
2	4	6	)	<	30			118	4	23
3			54				44	array		133
4		156	4	53		<	49		133	<
	53		155		<	67	begin	♦	172	<
6	64		4	57	end	4	89	if		172
7	г hen	•	172		78		4	71		88
8	Г'ке	*	172		88		4	81	endif
9		105	<	102		99	<■ number. >	4	100	real ->
in	4	103		1	106			COUSt		=
11		237	<	117		4	108		C	130
12		126		107	4	128		414	4	132
13		208		1	<	153	<	141		4
14	148		90	<	148			90		153
15			136			of	*	310		fur
IC.	all		do	<	169		172		171	*
17	54			205	<	194	<	181		1
18	176		237		187		287		192	< operation'»
19		176		203	*	237	<	200	*	287
20	T=		172	4	207	*	159		<	234
21	<	217	node	*	414	i	232	<_	220	static
22	node	< tag >		232	(	' tag '	<	231
23	225	)	4	236		54		<_	276	<-
21	263	<	257	'4tag>	<	255	<	252	*	300
25	4	253	-	4	244	4	261	(		172
26	)		274	'-tag >	<	274	(		<	273
27		4	267	)	4	278	*	90		pointer
28	iff	286		285	to	^tag>		(<8		298
29	c	295	input	4	296	output	4	299
30		*	388		308		4	301	1
31		385		381		374		371		368
32		365		362		359		356		353
33	<	350	•<	347	<	344	<	341	bool
34	342	byte	4	345	char	4	348	dword	4	351
35	ни	4	354	lougiut	4	357	shortint	4	.360	word
3G	4	363	bit row	4	366	double	4	369	pointer	4
37	372	real	4	375	string	<	379		<. number" >	4
38	383		279	4	387		35			404
39		400	c	397		4	398	all	4	402
40		172	4	413	(		388	<	412
41	4	405	)			<	420		1	414
42			310	<	428		4	414

Рис. 6. Линейное представление граф-схемы Yard

S_first = { { ’program’ -ЗУ , { ’static’ - 2 У }

S_2 = { ’program’ - 3 }

S_3 = { ’’ - 4 У

S_4 = { ’(’ - 20 У

S_16 = { { ’)’ - 28 У , { ’,’ - 20 У У

S_20 = { { ’’ - 16 У , { ’output’ - 16 У , { ’input’ - 16 У У

S_25 = ( { ( { ( { < ’if’ - 67 У , { ’begin’ - 62 У У , Compoundstatement - 427 ) , ■( ’node’ - 220 У , { ’static’ - 219 } , { ’node’ - 212 У У , NodeDeclaration - 427 ) , ( { ’’ - 414 У , VariableDeclaration - 427 ) ,  ( { ’const’ - 115 У ,

ConstantDeclaration - 427 ) У , Declaration - 28 )

S_28 = { { ';’ - 30 } , { ’;’ - 25 } }

S_30 = ( { ■( ’if’ - 67 У , { ’begin’ - 62 У У , Compoundstatement - 32 )

S_32 = { ’.’ - 427 }

S_37 =  (  { ’ [’ - 133 У  , FormalBounds - 39 )

S_39 =  (  { ’of’ - 155 У  , FormalComponent - 427 )

S_44 =  {  { F У ,   ( ■( ’of’ - 155 У , FormalComponent - 427 )   ,  (

•[ ’ [’ - 133 У , FormalBounds - 48 ) У

S_48 =  {  { F У ,   ( ■( ’of’ - 155 У , FormalComponent - 427 )  У

S_58 =  {  { ’end’ - 427 } , { ’;’ - 62 } }

S_62 = ( { ( { ’for’ - 159 У , ForStatement - 427 ),({({ •{ ’’ - 427 У , { ’’ - 427 У , { ’’ - 427 У

Рис. 7. Состояния распознавателя

Всего 427 состояний, которые после минимизации автомата свелись к 68 состояниям (уменьшение на 84%).

Проверим построенный распознаватель на следующих двух тестах, показанных в экранном варианте на рисунках 8, 9.

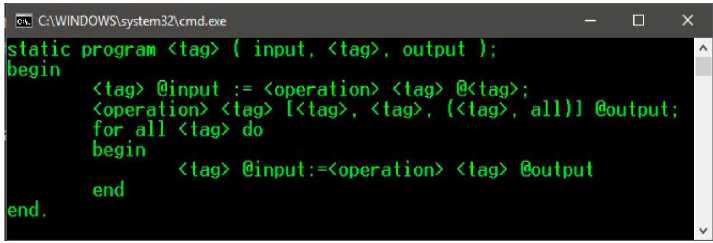
Рис. 8. Пример входной цепочки

Теперь внесем в данный тест ошибку (например, удалим "<" из середины цепочки). Результат будет следующим:

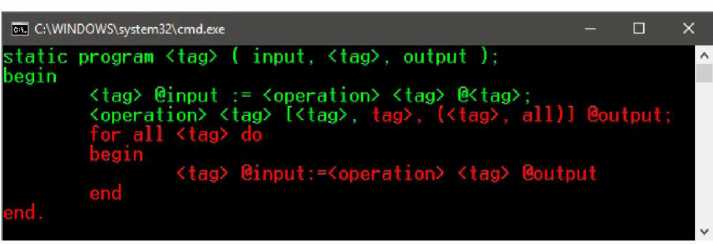
Рис. 9. Тест с ошибкой

Текст после ошибки подсвечен красным цветом.

Заключение

В результате проделанной работы была построена МП-таблица состояний распознавателя языка Yard, которая может быть использована далее при построении анализатора. Цель на будущее — обеспечить конкурентное преимущество для новых чипов, снабдив их компилятором и библиотекой программных решений, разработанных на основе инструментальной системы SynGT.