Построение решений уравнения колебаний балки переменного сечения

Рассмотрим балку постоянной ширины и линейно изменяющейся толщины

h = ht +

⁽h₀-h i ⁾x

L

,

где h_v - толщина в сечении x = 0, h₀ толщина в сечении x = L, где L длина балки. Для конической балки площадь сечения и момент инерции задаются следующим образом

b h ³

"12"

b [h^L + (h₀—h₁)x]³

12L3

А = bh = ЬрЧ + (ho-

^, h_v)x/L].

Тогда уравнение, описывающее колебание конической балки будет иметь вид

d2

^ dx2

b [h_TL + (ho—h-^xp d²u

12L3

dx2

-

pba) ² h_t +

(h₀-h i )x’

L

u = 0.(1)

Введем новую переменную

z = ht +

(ho-h-^x

.

Уравнение (1) примет вид

L

d2 ( dz2 Г

„ d2u\

^^=2*^®

где

12pw²L⁴ = E(h₀-h i )⁴.

k4

Решение уравнения (2) будем искать в виде степенного ряда

ОО u = ^ zn+y . (3)

П = 0

Подставляя (3) в (2), получим общее решение уравнения (2)

[CiA(2kV5) + C 2 / i (2kV^) + С з У 1 (2кТ^) + C₄K i (2kV^)]

u(x) = --------------------------—-------------------------, (4)

NZ где /1; 1г, 1, , К, - функция Бесселя, модифицированная функция Бесселя, функция Хан-келя, функция Макдональда. Решение (4) было впервые получено в работе [1].

Свободные колебания балки с переменным сечением описываются уравнением

d2 (d

77777 )^( x )     - pAai²u =0․(5)

dxz I

Это уравнение можно переписать следующим образом d^u         d^ud

^-777 +2 m^^{m 1}3tt + m ( m -1)Г"²^-Ω ²^^mu =0,(6)

где

x _   оЛ<у2£4

․

,Ω2 = _-----

,Ω =

Умножая уравнение (6) на     и, полагая 6 =4- m + n , получим

.d^u        d3u , rn

777+2      + m ⁽ m -1)     -Ω ²^^eu =0, (7)

Введем следующие обозначения

Ω2ed v =,Lu =․

,

Тогда, уравнение (7) примет вид

2-

—)lL“-

Lu Lu - — I I Lu - \       6 / \

3- m\

—-—и - uv =0․(8)

6 /

Уравнение (8) представляет собой обобщенное гипергеометрическое уравнение [3]. Общим решением этого уравнения является линейная комбинация линейно независимых гипергеометрических функций иг =       (–1; -bi, Ьг, Ьз ;v),(9i)

u₂ =         (–1; 2- bi , Ьз - bi +1, Ьз - bi +1; v ),(92)

U₃ =         (–1; bl ^- b₂ +1,2- b₂ , Ьз ^- b₂ +1; v ),(9з)

u₄ =         (–1; bi ^- Ьз +1, b₂ ^- Ьз +1,2- Ьз ; и ),(94)

где

3- m + и       2+ и       1+ и

=           ,       =      ,       =

0^3

п( bj )п^!

7 = 1

Функции (9) будут либо не определены, либо не будут линейно независимыми, если ^1 , ^2 , jbg целые числа или разность любых двух из них целое число. Для этих случаев в общих решениях появляются логарифмические члены. Подробный вывод логарифмических решений методом Фробениуса были представлены в работе [4] и здесь они не приводятся. Wang [1] рассмотрел следующие четыре случая: (а) когда два коэффициента равны (это возникает, если т = 1 или т = 2 или т = 4, что влечет ^1 = ); (b) когда один из коэффициентов равен единице (действительно, при т = 2 или т = 3, значение ^1 или ^3 равно единице; (c) когда ^1 является отрицательным целым числом или нулем (это происходит, когда 9 является обратным к положительному целому числу); (d) когда разность двух коэффициентов есть целое число (например, комбинация т = 3 и и = 1 дает ^1=1/2 и^3 = 3/2, которые имеют разность равную единице.) Некоторые частные случаи можно получить из общей формулы (9). Для однородной балки, т. е. т = = 0, 0 = 4 и ^1 = 3/4, ^2 = 2/4, /?з =1/4 гипергеометрические функции сводятся к известному решению

и ( X )=Ci sin( кх )+ С₂ cos( кх )+ С₃с ℎ( кх )+ C₄s ℎ( кх )․

Другой частный случай возникает при т - п = 2 или 6 = 2 и включает в себя клиновидные и конусообразные балки. В этом случае решение сводится к функциям Бесселя [2]

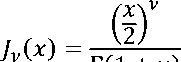
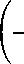
1+v;

-

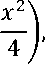
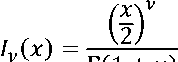
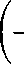
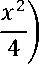
Последний частный случай относится к балке с постоянной толщиной и линейно изменяющейся шириной. Здесь т= = 1, и ^1 = 3/4, ^2 = 3/4, Ьд = 1/2. Так как значения ^1 , ^2 равны, то решения 1Л-^ , ^•2 совпадают, и решение 1^2 будет иметь вид и2 =     -4%4

5∙45∙3

15+13+12 )“ +

44  44  111111\ 2

9∙82∙75∙42∙3 9⁺7⁺5⁺9⁺7⁺5 )и ₊